Three Essays on Transport Economics and Policy
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Folkemøte Namsskogan Kommune
Folkemøte Namsskogan kommune Strategi- og forankringsfasen 15. februar 2021 Velkommen til folkemøte 19.00: Velkommen v/ ordfører Stian Brekkvassmo Informasjon om bakgrunn og målsetting med prosjektet 19.10: John Håvard Solum, banksjef i Grong Sparebank Muligheter for nærings- og samfunnsutvikling i et regionalt perspektiv 19.20: Sandra Staldvik, prosjektleder Bosetting, Namsskogan kommune Økt tilflytting og bolyst i Namsskogan - mål og innhold i Bolystprosjekt 19.25: Johannes Skaar, Innovasjon Norge og Even Ystgård, Trøndelag Fylkeskommune Introduksjon til omstillingsprogrammet og rollen til Innovasjon Norge og fylkeskommunen 19.35: PwC v/ Ingvill Flo og Randi Ness Innhold og arbeidsform i Strategi- og forankringsfasen Lokalt perspektiv på næringsutvikling i regionen 19.45: Åpen runde med innspill fra innbyggere og næringsliv Ordstyrer Silje Guddal, PwC 2 Innledning digitalt folkemøte – 15.02.2021 Dagens oppslag i NRK Vi inngikk samarbeid med Distriktssenteret Aha-opplevelse Valg av bosted Vi dro på studietur Namsskogan har satset 8 millioner! Namsskogan Prosjektleder Utvikling AS Bosetting Eget Næringsselskap i kommunen mellom Sandra næringslivet og kommunen Staldvik Daglig leder Jens Petter Aarli Sysselsettingsutvikling Sysselsettingsutviklingen har vært svakere i nabokommunene Røyrvik og Høylandet i perioden 2010-2019. Lierne er på samme nivå, mens Grong har hatt ganske flat utvikling og er på -2,4 i forhold til 2010. Grane kommune på andre siden av fylkesgrensa er har hatt vekst med +14% i perioden, mens Hattfjelldal har hatt en nedgang på -14%.Den negative utviklingen i nærområdene kan også bidra til å begrense mulighetene for pendling fra Namsskogan til andre kommuner. Og kan dermed på sikt legge ytterligere press på befolkningsgrunnlaget for kommunen siden det for personer som ikke finner jobb i kommunen vil være færre sysselsettingsmuligheter som ikke innebærer flytting. -

Møteplan for Kommunestyrer Og Formannskap I Kommuner I Namdalen Høst 2018
Møteplan for kommunestyrer og formannskap i kommuner i Namdalen høst 2018 Uke Dato Mandag Dato Tirsdag Dato Onsdag Dato Torsdag Dato Fredag 36 03.09 04.09 Namsos FOR 05.09 Osen FOR 06.09 Namdalseid FOR 07.09 Røyrvik FOR Overhalla FOR Lierne KOM 37 10.09 Nærøy FOR 11.09 Grong FOR 12.09 Fosnes FOR 13.09 Flatanger KOM 14.09 Lierne FOR Namdalseid FOR Røyrvik KOM Høylandet FOR Grong KOM 38 17.09 Høylandet KOM 18.09 Flatanger FOR 19.09 Osen KOM 20.09 Vikna KOM 21.09 Nærøy KOM Namsos FOR Leka FOR Namsskogan KOM Vikna FOR Overhalla KOM 39 24.09 25.09 26.09 27.09 Namsos KOM 28.09 Fosnes KOM Leka KOM 40 01.10 02.10 Namsos FOR 03.10 Røyrvik FOR 04.10 Namdalseid FOR 05.10 Namsskogan FOR (Fosnes FOR) Overhalla FOR Lierne FOR 41 08.10 09.10 10.10 Nærøy FOR 11.10 12.10 (Fosnes FOR) 42 15.10 16.10 Namsos FOR 17.10 18.10 Høylandet FOR 19.10 Namsskogan KOM Grong FOR Osen FOR Vikna FOR 43 22.10 Overhalla KOM 23.10 Flatanger FOR 24.10 Osen KOM 25.10 Namdalseid FOR 26.10 Røyrvik KOM Leka FOR Namsos KOM Lierne FOR Fosnes KOM Høylandet KOM Grong KOM Vikna KOM 44 29.10 30.10 Namsos FOR 31.10 Leka KOM 01.11 Flatanger KOM 02.11 Namsskogan FOR Namdalseid KOM Lierne FOR Høylandet FOR 45 05.11 06.11 Overhalla FOR 07.11 Nærøy FOR 08.11 09.11 Lierne FOR Osen FOR Leka FOR Røyrvik FOR 46 12.11 13.11 Flatanger FOR 14.11 Fosnes FOR 15.11 16.11 Nærøy KOM Namsos FOR Høylandet FOR Namsskogan KOM Vikna FOR 47 19.11 20.11 Vikna KOM 21.11 Osen KOM 22.11 Høylandet KOM 23.11 Overhalla KOM Leka FOR Vikna FOR Lierne FOR Røyrvik KOM 48 26.11 27.11 Namsos FOR 28.11 Fosnes FOR 29.11 Namsos KOM 30.11 Nærøy FOR Fosnes KOM Namsskogan FOR Høylandet KOM Grong FOR Grong KOM Leka KOM Lierne KOM 49 03.12 Overhalla FOR 04.12 Flatanger FOR 05.12 Osen FOR 06.12 Høylandet FOR 07.12 Røyrvik FOR 50 10.12 Lierne FOR 11.12 Namsos FOR 12.12 13.12 Namdalseid KOM 14.12 Høylandet KOM Namsskogan KOM Namsos KOM Fosnes KOM Grong FOR Vikna KOM 51 17.12 Vikna FOR 18.12 Nærøy KOM 19.12 Osen KOM 20.12 Flatanger KOM 21.12 Overhalla KOM Grong KOM Røyrvik KOM KOM: Kommunestyremøte FOR: Formannskapsmøte . -

Brass Bands of the World a Historical Directory
Brass Bands of the World a historical directory Kurow Haka Brass Band, New Zealand, 1901 Gavin Holman January 2019 Introduction Contents Introduction ........................................................................................................................ 6 Angola................................................................................................................................ 12 Australia – Australian Capital Territory ......................................................................... 13 Australia – New South Wales .......................................................................................... 14 Australia – Northern Territory ....................................................................................... 42 Australia – Queensland ................................................................................................... 43 Australia – South Australia ............................................................................................. 58 Australia – Tasmania ....................................................................................................... 68 Australia – Victoria .......................................................................................................... 73 Australia – Western Australia ....................................................................................... 101 Australia – other ............................................................................................................. 105 Austria ............................................................................................................................ -

680 Levanger > Steinkjer > Namsos Effective from August 25 Th 2021 / V.4 Mandag - Fredag / Monday - Friday
Ruta krysser sonegrense. Pass på at du har riktig billett. Se atb.no/soner This route crosses zone-limits. Make sure you have the correct ticket. See atb.no/en/zones Gjelder fra 25. august 2021 / v.4 680 Namsos > Steinkjer > Levanger Effective from August 25 th 2021 / v.4 mandag - fredag / Monday - Friday Kjøres kun* / Operates only* Namsos skysstasjon N1 05:30 06:30 07:30 AR 08:30 R 09:40 AH 10:40 11:40 12:40 13:40 14:40 Sykehuset Namsos 05:33 06:33 07:33 08:33 09:43 10:43 11:43 12:43 13:43 14:43 Hylla 05:35 06:35 07:35 08:35 A 09:45 10:45 11:45 12:45 13:45 14:45 Klinga vegdele 05:45 06:45 B 07:45 D 08:45 D 09:55 10:55 11:55 12:55 13:55 14:55 Bangsund vegdele 05:50 06:50 07:50 08:50 10:00 11:00 12:00 13:00 14:00 15:00 Sjøåsen 06:05 07:05 B 08:05 09:05 B 10:15 B 11:15 12:15 13:15 14:15 B 15:15 Fossli vegdele 06:10 07:10 08:10 09:10 I 10:20 11:20 12:20 13:20 14:20 15:20 J Namdalseid 06:15 07:15 08:15 09:15 10:25 11:25 12:25 13:25 14:25 15:25 Østvik 06:32 B 07:32 B 08:32 B 09:32 B 10:42 B 11:42 B 12:42 B 13:42 14:42 B 15:42 B Asp 06:42 07:42 08:42 09:41 10:52 11:51 12:51 13:51 14:51 15:51 Dampsaga 06:48 07:48 08:48 09:46 10:58 11:56 12:56 13:56 14:56 15:56 Nordsida 06:48 07:48 08:48 09:46 10:58 11:56 12:56 13:56 14:56 15:56 Steinkjer stasjon S1 | ||||||||16:01 T Steinkjer stasjon S2 06:56 T 06:00 07:56 T 08:56 T 09:49 T 11:06 T 11:59 FT 12:59 T 13:59 T 14:59 FT Steinkjer montessoriskole | | | | 09:57 | 12:07 13:07 14:07 15:07 Sparbu 07:09 06:15 08:09 09:09 11:19 Sulkrysset 07:26 06:30 08:26 09:26 11:36 Levanger stasjon 07:41 06:45 08:41 -

Kommunereformen – Sammenslåing Eller Overhalla Som Egen Kommune
Kommunereformen Sammenslåing av Overhalla med Fosnes, Flatanger, Høylandet, Namdalseid og Namsos eller Overhalla fortsatt som egen kommune? Foreløpig vurdering - fordeler og ulemper. Kommunereformen – sammenslåing eller Overhalla som egen kommune Innhold: Innhold 1. Bakgrunn.............................................................................................................................................. 3 2. Mål og kriterier for framtidig kommunestruktur ................................................................................ 5 3. Om geografi, bosetting og befolkning ................................................................................................. 6 4. Økonomi. ........................................................................................................................................... 12 5. Kommunen som tjenesteyter ............................................................................................................ 16 6. Kommunen som myndighetsutøver .................................................................................................. 19 7. Kommunen som samfunnsutvikler.................................................................................................... 20 8. Kommunen som lokaldemokratisk arena.......................................................................................... 21 Foreløpig vurdering – fordeler og ulemper Side 2 Kommunereformen – sammenslåing eller Overhalla som egen kommune 1. Bakgrunn Overhalla kommune har siden høsten 2014 arbeidet -
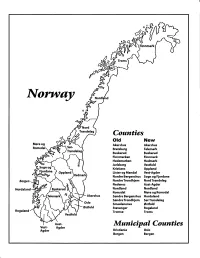
Norway Maps.Pdf
Finnmark lVorwny Trondelag Counties old New Akershus Akershus Bratsberg Telemark Buskerud Buskerud Finnmarken Finnmark Hedemarken Hedmark Jarlsberg Vestfold Kristians Oppland Oppland Lister og Mandal Vest-Agder Nordre Bergenshus Sogn og Fjordane NordreTrondhjem NordTrondelag Nedenes Aust-Agder Nordland Nordland Romsdal Mgre og Romsdal Akershus Sgndre Bergenshus Hordaland SsndreTrondhjem SorTrondelag Oslo Smaalenenes Ostfold Ostfold Stavanger Rogaland Rogaland Tromso Troms Vestfold Aust- Municipal Counties Vest- Agder Agder Kristiania Oslo Bergen Bergen A Feiring ((r Hurdal /\Langset /, \ Alc,ersltus Eidsvoll og Oslo Bjorke \ \\ r- -// Nannestad Heni ,Gi'erdrum Lilliestrom {", {udenes\ ,/\ Aurpkog )Y' ,\ I :' 'lv- '/t:ri \r*r/ t *) I ,I odfltisard l,t Enebakk Nordbv { Frog ) L-[--h il 6- As xrarctaa bak I { ':-\ I Vestby Hvitsten 'ca{a", 'l 4 ,- Holen :\saner Aust-Agder Valle 6rrl-1\ r--- Hylestad l- Austad 7/ Sandes - ,t'r ,'-' aa Gjovdal -.\. '\.-- ! Tovdal ,V-u-/ Vegarshei I *r""i'9^ _t Amli Risor -Ytre ,/ Ssndel Holt vtdestran \ -'ar^/Froland lveland ffi Bergen E- o;l'.t r 'aa*rrra- I t T ]***,,.\ I BYFJORDEN srl ffitt\ --- I 9r Mulen €'r A I t \ t Krohnengen Nordnest Fjellet \ XfC KORSKIRKEN t Nostet "r. I igvono i Leitet I Dokken DOMKIRKEN Dar;sird\ W \ - cyu8npris Lappen LAKSEVAG 'I Uran ,t' \ r-r -,4egry,*T-* \ ilJ]' *.,, Legdene ,rrf\t llruoAs \ o Kirstianborg ,'t? FYLLINGSDALEN {lil};h;h';ltft t)\l/ I t ,a o ff ui Mannasverkl , I t I t /_l-, Fjosanger I ,r-tJ 1r,7" N.fl.nd I r\a ,, , i, I, ,- Buslr,rrud I I N-(f i t\torbo \) l,/ Nes l-t' I J Viker -- l^ -- ---{a - tc')rt"- i Vtre Adal -o-r Uvdal ) Hgnefoss Y':TTS Tryistr-and Sigdal Veggli oJ Rollag ,y Lvnqdal J .--l/Tranbv *\, Frogn6r.tr Flesberg ; \. -

Poststeder Nord-Trøndelag Listet Alfabetisk Med Henvisning Til Kommune
POSTSTEDER NORD-TRØNDELAG LISTET ALFABETISK MED HENVISNING TIL KOMMUNE Aabogen i Foldereid ......................... Nærøy Einviken ..................................... Flatanger Aadalen i Forradalen ...................... Stjørdal Ekne .......................................... Levanger Aarfor ............................................ Nærøy Elda ........................................ Namdalseid Aasen ........................................ Levanger Elden ...................................... Namdalseid Aasenfjorden .............................. Levanger Elnan ......................................... Steinkjer Abelvær ......................................... Nærøy Elnes .............................................. Verdal Agle ................................................ Snåsa Elvalandet .................................... Namsos Alhusstrand .................................. Namsos Elvarli .......................................... Stjørdal Alstadhoug i Schognen ................. Levanger Elverlien ....................................... Stjørdal Alstadhoug ................................. Levanger Faksdal ......................................... Fosnes Appelvær........................................ Nærøy Feltpostkontor no. III ........................ Vikna Asp ............................................. Steinkjer Feltpostkontor no. III ................... Levanger Asphaugen .................................. Steinkjer Finnanger ..................................... Namsos Aunet i Leksvik .............................. -
Rural Infant Mortality in Nineteenth Century Norway1
Rural Infant Mortality in Nineteenth Century Norway1 Gunnar Thorvaldsen uch previous research on the Norwegian mortality decline has focused on specific localities, employing databases with linked microdata. One Mgood choice is Rendalen, a parish on the Swedish border, representative of the world record low Norwegian mortality rates. The focus on the role of women, given their access to more abundant material resources towards the end of the eighteenth century, is a most interesting explanation for the declining level of infant mortality.2 Another well-researched locality is the fjord-parish Etne, south of Bergen, where infant mortality was significantly higher – also an area where the role of women is highlighted. More recent studies have been done on Asker and Bærum, south of Oslo, with infant mortality levels closer to the national average. The present article will not attempt to match these penetrating studies of well- researched rural localities, nor William Hubbard’s insights into many aspects of urban mortality.3 Rather it broadens the scope to include the whole country. My study is limited primarily to Norway’s sparsely populated rural areas, where 90 percent of the population lived in 1801, a figure that was declining towards 60 percent by 1900, when the national infant mortality rate (IMR) had fallen below ten percent.4 My basic aim is to track the development of infant mortality rates in Norway over time, and, where possible, to say something about regional differences in the proportion of children who died before they reached their first birthday. The 1 Another version of this article will also be published inStudies in Mortality Decline. -

Administrative and Statistical Areas English Version – SOSI Standard 4.0
Administrative and statistical areas English version – SOSI standard 4.0 Administrative and statistical areas Norwegian Mapping Authority [email protected] Norwegian Mapping Authority June 2009 Page 1 of 191 Administrative and statistical areas English version – SOSI standard 4.0 1 Applications schema ......................................................................................................................7 1.1 Administrative units subclassification ....................................................................................7 1.1 Description ...................................................................................................................... 14 1.1.1 CityDistrict ................................................................................................................ 14 1.1.2 CityDistrictBoundary ................................................................................................ 14 1.1.3 SubArea ................................................................................................................... 14 1.1.4 BasicDistrictUnit ....................................................................................................... 15 1.1.5 SchoolDistrict ........................................................................................................... 16 1.1.6 <<DataType>> SchoolDistrictId ............................................................................... 17 1.1.7 SchoolDistrictBoundary ........................................................................................... -

Høylandet Kommune Sted, 30.06.2021
Høylandet kommune Sted, 30.06.2021 Høylandet kommune Informasjon om kollektivtilbudet fra 7. august Lørdag 7. august starter det nye kollektivtilbudet med buss og fleksibel transport i Trøndelag. Sammen med tog vil dette utgjøre det totale kollektivtilbudet i ditt område. Vi gjør oppmerksom på at det kan komme enkelte justeringer i tilbudet frem mot oppstarten 7. august. Dette oppdateres fortløpende på atb.no/trondelag Slik reiser du Når du skal reise i, eller til og fra Høylandet, kan du bruke regionlinjer og tog i kombinasjon med fleksibel transport. Skolelinjer og fleksibel transport kan benyttes av alle. Fleksibel transport For å reise kollektivt til og fra holdeplass kan du bestille fleksibel transport. Billettprisen er den samme for buss og fleksibel transport. Fleksibel transport er åpen for alle reisende. Bestill fleksibel transport på telefon 02867. Les mer om soner og annen informasjon om fleksibel transport på atb.no/hoylandet. Dette blir nytt fra 7. august • Linje 660 Rørvik – Kolvereid – Foldereid – Namsos har kun avganger til og fra Namsos fredag og søndag. På hverdager kan du benytte linje 695 (Harran) – Grong – (Høylandet) – Overhalla – Namsos til Namsos. • Linje 685 Høylandet - Namsos fjernes. Avgangene flyttes til linje 695. • Linje 695 får en ekstra kveldsavgang kl. 18:30 fra Namsos til Høylandet på hverdager. Nye busser I august kommer nye og komfortable busser på alle linjer. Mange av bussene får sanntidsskjerm som viser neste holdeplass, i tillegg til annonsering over høyttaler om bord. Ny app AtB Appen AtB er utviklet spesielt for reisende i Trøndelag og skal etter hvert dekke alle behov du måtte ha som reisende. -

Cruise Excursions
TRØNDELAG TRONDHEIM CRUISE EXCURSIONS Photo: Steen Søderholm / trondelag.com Photo: Steen Søderholm / trondelag.com TRONDHEIM Photo: Marnie VIkan Firing Photo: Trondheim Havn TRONDHEIM TRØNDELAG THE ROYAL CAPITAL OF NORWAY THE HEART OF NORWEGIAN HISTORY Trondheim was founded by Viking King Olav Tryggvason in AD 997. A journey in Trøndelag, also known as Central-Norway, will give It was the nation’s first capital, and continues to be the historical you plenty of unforgettable stories to tell when you get back home. capital of Norway. The city is surrounded by lovely forested hills, Trøndelag is like Norway in miniature. Within few hours from Trond- and the Nidelven River winds through the city. The charming old heim, the historical capital of Norway, you can reach the coastline streets at Bakklandet bring you back to architectural traditions and with beautiful archipelagos and its coastal culture, the historical the atmosphere of days gone by. It has been, and still is, a popular cultural landscape around the Trondheim Fjord and the mountains pilgrimage site, due to the famous Nidaros Cathedral. Trondheim in the national parks where the snow never melts. Observe exotic is the 3rd largest city in Norway – vivid and lively, with everything animals like musk ox or moose in their natural environment, join a a big city can offer, but still with the friendliness of small towns. fishing trip in one of the best angler regions in the world or follow While medieval times still have their mark on the center, innovation the tracks of the Vikings. If you want to combine impressive nature and modernity shape it. -

Forskrift Om Sammenslåing Fosnes, Namdalseid Og Namsos
Forskrift om sammenslåing av Fosnes kommune, Namdalseid kommune og Namsos kommune til Namsos kommune Fastsatt av Kommunal- og moderniseringsdepartementet 22. februar 2018 med hjemmel i kommuneloven § 3 nr. 3 og inndelingslova § 17, jf. kongelig resolusjon 27. oktober 2017 nr. 1666. § 1. Fosnes kommune, Namdalseid kommune og Namsos kommune slås sammen til én kommune fra 1. januar 2020. Navnet på kommunen er Namsos kommune. § 2. Kommunestyret skal ha 41 medlemmer, inntil kommunestyret eventuelt bestemmer annet i medhold av kommuneloven § 7 nr. 3. § 3. Vedtekter og forskrifter som er gjeldende i Fosnes kommune, Namdalseid kommune og Namsos kommune skal fortsatt gjelde for vedkommende områder inntil nye lokale vedtekter og forskrifter er fastsatt av kommunestyret. Frist for fastsetting av nye vedtekter og forskrifter er 1. januar 2021. § 4. Fellesnemnda skal sørge for at sammensetningen av kommunens forliksråd er i samsvar med domstolloven § 27 og § 57 i perioden fra sammenslåingstidspunktet til nytt forliksråd trer i funksjon. Fellesnemnda kan fastslå at virketiden for de eksisterende forliksrådene i kommunene skal videreføres slik at den nye kommunen har to eller flere forliksråd i en periode. § 5. Kommuneplaner og kommunedelplaner etter plan- og bygningsloven kapittel 11, inkludert arealdelen, gjelder inntil de erstattes av nye planer vedtatt av det nye kommunestyret. Reguleringsplaner etter lovens kapittel 12 gjelder inntil de erstattes av nye planer eller de vedtas opphevet. § 6. I en overgangsperiode fra 1. januar 2020 til 31. desember 2021 gis Namsos kommune unntak fra eigedomsskattelova slik at eiendomsskatteregimene som gjaldt i Fosnes kommune, Namdalseid kommune og Namsos kommune kan videreføres for vedkommende områder i overgangsperioden i den grad disse var i overensstemmelse med eigedomsskattelova.