Shading Calculations for the Radiation Instruments at Jabiru
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Annual Report 19
Darwin Alice Springs Tennant Creek A Airport Development Group International Airport Airport Airport Annual Report 19 . Highlights 2018–19 We reached a milestone The National Critical Care In October 2018, Alice Springs of 21 years since the three and Trauma Response Centre received the first of four airports were privatised was completed at Darwin charter flights from Tokyo, under the NT Airports International Airport in Nagoya and Osaka, Japan, in banner, celebrating with April 2019, creating a world- more than 10 years. a special airside premiere class, on-airport Emergency screening of the aviation Medical Retrieval Precinct. history film ‘The Sweet Little Note of the Engine.’ Virgin Australia launched a new three-times-weekly We refurbished an seasonal service to Denpasar, underused part of the Bali, in April 2019. Sustainability reporting Darwin terminal into the introduced. Emissions target ‘Green Room’, a pop-up developed and on track to community arts space, have zero net emissions by launching it in August 2018. SilkAir announced an 2030 (scope 1 and 2). increase in weekly services between Darwin and Singapore from July 2019, Ian Kew, CEO, continued marking its seventh year of Runway overlay works as Chairman of the Darwin operations to Darwin with a commenced in Alice Springs Major Business Group and seventh weekly service. at a value of circa Chairman of the Darwin $20 million. Festival. ADG staff and the company contributed $18,000 to two ‘Happy or Not’ instant community causes from our $1.4 million infrastructure customer feedback Workplace Giving initiative. boost at Tennant Creek platforms installed in Alice for improved fencing and Springs and Darwin. -

COVID-19 UPDATE – 21St January 2021
COVID-19 UPDATE – 21st January 2021 MANDATORY FACE MASKS REQUIRED AT GOVE AIRPORT On Friday 8th January 2021, the Prime Minister announced (National Cabinet agreed) mandatory use of masks in domestic airports and on all domestic commercial flights. Furthermore, the NT Chief Health Officer Directions make it mandatory from the 20th January 2021 for face masks to be worn at all major NT airports and while on board an aircraft. Masks must be worn when inside the airport terminal building and when on the airfield. Children under the age of 12 and people with a specified medical condition are not required to wear a mask. Mask wearing is mandatory at the following Northern Territory airports: • Darwin International Airport • Alice Springs Airport • Connellan Airport - Ayers Rock (Yulara) • Gove Airport • Groote Eylandt A person is not required to wear a mask during an emergency or while doing any of the following: • Consuming food or beverage • Communicating with a person who is hearing impaired. • Wearing an oxygen mask AIRPORT & TRAVELLING • PLEASE NOTE: To reduce the challenges with social distancing and to minimise risks, only Airline passengers will be able to enter the Airport terminal, • please drop-off and pick-up passengers outside of the terminal building It is the responsibility of individuals to make sure they have a mask to wear when at major NT airports and while on board an aircraft. Additional Information: • Please be aware of the NT Government Border Controls, which may be in place https://coronavirus.nt.gov.au/travel/interstate-arrivals • https://www.interstatequarantine.org.au/state-and-territory-border-closures/ • AirNorth schedule - https://www.airnorth.com.au/flying-with-us/before-you-fly/arrivals- and-departures • https://www.cairnsairport.com.au/travelling/airport-guide/covid19/ . -

Document Title
COVID-19 Management Plan COVID-19 Management Plan Table of Contents 1 Distribution List ........................................................................................................................................ 4 1.1 Copies ............................................................................................................................................. 4 2 Amendment Record ................................................................................................................................. 4 3 Purpose .................................................................................................................................................... 4 3.1 Scope .............................................................................................................................................. 4 3.2 Documentation ................................................................................................................................ 4 4 Approvals ................................................................................................................................................. 5 5 Introduction .............................................................................................................................................. 5 5.1 Spread ............................................................................................................................................. 5 5.2 Symptoms ...................................................................................................................................... -

Northern Territory June 2012 Monthly Weather Review Northern Territory June 2012
Monthly Weather Review Northern Territory June 2012 Monthly Weather Review Northern Territory June 2012 The Monthly Weather Review - Northern Territory is produced twelve times each year by the Australian Bureau of Meteorology's Northern Territory Climate Services Centre. It is intended to provide a concise but informative overview of the temperatures, rainfall and significant weather events in Northern Territory for the month. To keep the Monthly Weather Review as timely as possible, much of the information is based on electronic reports. Although every effort is made to ensure the accuracy of these reports, the results can be considered only preliminary until complete quality control procedures have been carried out. Major discrepancies will be noted in later issues. We are keen to ensure that the Monthly Weather Review is appropriate to the needs of its readers. If you have any comments or suggestions, please do not hesitate to contact us: By mail Northern Territory Climate Services Centre Bureau of Meteorology PO Box 40050 Casuarina NT 0811 AUSTRALIA By telephone (08) 8920 3813 By email [email protected] You may also wish to visit the Bureau's home page, http://www.bom.gov.au. Units of measurement Except where noted, temperature is given in degrees Celsius (°C), rainfall in millimetres (mm), and wind speed in kilometres per hour (km/h). Observation times and periods Each station in Northern Territory makes its main observation for the day at 9 am local time. At this time, the precipitation over the past 24 hours is determined, and maximum and minimum thermometers are also read and reset. -

Company Profile
Commercial & Industrial Electrical & Mechanical Contracting, Fibre Optics, Communications, Data, Security, MATV, CCTV, Fire, Control Systems, Lightning Protection Systems High Voltage reticulation, Transformers Accredited PowerWater Contractor ABN 20 062 315 137 Company Profile Kellyco Electrical Services Pty Ltd was established in 1993 in Alice Springs. The company has enjoyed successful growth and expansion over the last 25 years, which has enabled us to establish an enviable reputation for professionalism and reliability. Our Darwin operation was opened in September 2008 and in 2012 we became an accredited member of Master Electricians. Kellyco initially specialised in remote area commercial and industrial projects. In 2001 we diversified and expanded completing more complex commercial projects in Alice Springs and Darwin. Over the last 25 years we have developed a sound infrastructure including over 20 registered vehicles and plant equipment, we hold Electrical Contracting Licences for Northern Territory and South Australia. Please find our NT Contractors Accreditation to give you an idea our Certificate Levels. Kellyco can offer a complete installation package for Commercial , High Rise, Large Residential Projects and Industrial Electrical Installations, Data (20 year Madison certified), Fibre Optic Cabling, Data and Communications, MATV, CCTV, Security, Fire, PA Systems, Lightning Protection, Control Systems, High Voltage Reticulation, Transformers, Low Voltage reticulation. We also manage our own Design and Construct packages all to AS/NZ standards. Federal Safety System Kellyco are accredited members of the Master Electricians Association which includes the Federally recognised Safety Connect Electrical Safety Management System. Our SafetyConnect program is a comprehensive, personalised safety management programme designed to dovetail into pre‐existing Federally Accredited Principle run programmes. -

Airport Categorisation List
UNCLASSIFIED List of Security Controlled Airport Categorisation September 2018 *Please note that this table will continue to be updated upon new category approvals and gazettal Category Airport Legal Trading Name State Category Operations Other Information Commencement CATEGORY 1 ADELAIDE Adelaide Airport Ltd SA 1 22/12/2011 BRISBANE Brisbane Airport Corporation Limited QLD 1 22/12/2011 CAIRNS Cairns Airport Pty Ltd QLD 1 22/12/2011 CANBERRA Capital Airport Group Pty Ltd ACT 1 22/12/2011 GOLD COAST Gold Coast Airport Pty Ltd QLD 1 22/12/2011 DARWIN Darwin International Airport Pty Limited NT 1 22/12/2011 Australia Pacific Airports (Melbourne) MELBOURNE VIC 1 22/12/2011 Pty. Limited PERTH Perth Airport Pty Ltd WA 1 22/12/2011 SYDNEY Sydney Airport Corporation Limited NSW 1 22/12/2011 CATEGORY 2 BROOME Broome International Airport Pty Ltd WA 2 22/12/2011 CHRISTMAS ISLAND Toll Remote Logistics Pty Ltd WA 2 22/12/2011 HOBART Hobart International Airport Pty Limited TAS 2 29/02/2012 NORFOLK ISLAND Norfolk Island Regional Council NSW 2 22/12/2011 September 2018 UNCLASSIFIED UNCLASSIFIED PORT HEDLAND PHIA Operating Company Pty Ltd WA 2 22/12/2011 SUNSHINE COAST Sunshine Coast Airport Pty Ltd QLD 2 29/06/2012 TOWNSVILLE AIRPORT Townsville Airport Pty Ltd QLD 2 19/12/2014 CATEGORY 3 ALBURY Albury City Council NSW 3 22/12/2011 ALICE SPRINGS Alice Springs Airport Pty Limited NT 3 11/01/2012 AVALON Avalon Airport Australia Pty Ltd VIC 3 22/12/2011 Voyages Indigenous Tourism Australia NT 3 22/12/2011 AYERS ROCK Pty Ltd BALLINA Ballina Shire Council NSW 3 22/12/2011 BRISBANE WEST Brisbane West Wellcamp Airport Pty QLD 3 17/11/2014 WELLCAMP Ltd BUNDABERG Bundaberg Regional Council QLD 3 18/01/2012 CLONCURRY Cloncurry Shire Council QLD 3 29/02/2012 COCOS ISLAND Toll Remote Logistics Pty Ltd WA 3 22/12/2011 COFFS HARBOUR Coffs Harbour City Council NSW 3 22/12/2011 DEVONPORT Tasmanian Ports Corporation Pty. -

AO-2016-062 Final – 14 October 2016
Separation issue due to runway incursion involving Cessna 172, VH-EKV, and Beech 58, VH-MLB Alice Springs Airport, Northern Territory, 16 June 2016 ATSB Transport Safety Report Aviation Occurrence Investigation AO-2016-062 Final – 14 October 2016 Released in accordance with section 25 of the Transport Safety Investigation Act 2003 Publishing information Published by: Australian Transport Safety Bureau Postal address: PO Box 967, Civic Square ACT 2608 Office: 62 Northbourne Avenue Canberra, Australian Capital Territory 2601 Telephone: 1800 020 616, from overseas +61 2 6257 4150 (24 hours) Accident and incident notification: 1800 011 034 (24 hours) Facsimile: 02 6247 3117, from overseas +61 2 6247 3117 Email: [email protected] Internet: www.atsb.gov.au © Commonwealth of Australia 2016 Ownership of intellectual property rights in this publication Unless otherwise noted, copyright (and any other intellectual property rights, if any) in this publication is owned by the Commonwealth of Australia. Creative Commons licence With the exception of the Coat of Arms, ATSB logo, and photos and graphics in which a third party holds copyright, this publication is licensed under a Creative Commons Attribution 3.0 Australia licence. Creative Commons Attribution 3.0 Australia Licence is a standard form license agreement that allows you to copy, distribute, transmit and adapt this publication provided that you attribute the work. The ATSB’s preference is that you attribute this publication (and any material sourced from it) using the following wording: Source: Australian Transport Safety Bureau Copyright in material obtained from other agencies, private individuals or organisations, belongs to those agencies, individuals or organisations. -

10 Year Infrastructure Plan 2019–2028
ANNUAL REVIEW 10 YEAR INFRASTRUCTURE PLAN 2019–2028 CONTENTS Minister’s Foreword 2 Sectors 16 Northern Territory Cross Sector: Integrated Land Use 16 Economic Environment 3 and Infrastructure Planning Northern Territory Agribusiness, Fisheries and Aquaculture 24 Infrastructure Snapshot 4 Tourism 26 Territory-Wide Logistics Energy and Minerals 36 Master Plan 5 Defence and Related Industries 40 Government’s Infrastructure Focus 6 Education and Training 44 Economic Development Framework 8 Electricity 50 Partnering with the Private Sector 8 Water 54 Onshore Gas Industry Transport and Logistics 60 Development 10 Public Safety and Justice 72 Climate Change 12 Health 78 Development Levers 14 Housing 88 Sectors 15 Art, Culture and Active Recreation 94 Digital 104 Acknowledgements 107 Bibliography 108 How to navigate this document Government initiatives to encourage and support private sector investment are included on pages 8 to 11. Planned and proposed infrastructure projects are provided in each Sector commencing from page 18. The term ‘the Plan’ refers to the 10 Year Infrastructure Plan Annual Review 2019–2028. All statistics referred to in the Plan are based on 2017–18 unless otherwise indicated. Contents I 1 MINISTER’S FOREWORD The Northern Territory provides many opportunities for strategic private sector investment and the Northern Territory Government will support the growth and adaptability of local industry so it is strategically aligned with our growth sectors and global demand. The annual review of the 10 Year Infrastructure Plan This will bridge the gap for local industry to explore provides transparency in planning and prioritises investment diversity opportunities so they can continue projects identified as supporting the future growth and to sustain and grow through changing economic times. -
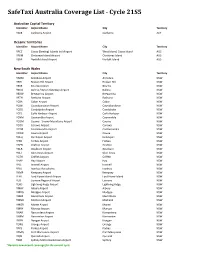
Safetaxi Australia Coverage List - Cycle 21S5
SafeTaxi Australia Coverage List - Cycle 21S5 Australian Capital Territory Identifier Airport Name City Territory YSCB Canberra Airport Canberra ACT Oceanic Territories Identifier Airport Name City Territory YPCC Cocos (Keeling) Islands Intl Airport West Island, Cocos Island AUS YPXM Christmas Island Airport Christmas Island AUS YSNF Norfolk Island Airport Norfolk Island AUS New South Wales Identifier Airport Name City Territory YARM Armidale Airport Armidale NSW YBHI Broken Hill Airport Broken Hill NSW YBKE Bourke Airport Bourke NSW YBNA Ballina / Byron Gateway Airport Ballina NSW YBRW Brewarrina Airport Brewarrina NSW YBTH Bathurst Airport Bathurst NSW YCBA Cobar Airport Cobar NSW YCBB Coonabarabran Airport Coonabarabran NSW YCDO Condobolin Airport Condobolin NSW YCFS Coffs Harbour Airport Coffs Harbour NSW YCNM Coonamble Airport Coonamble NSW YCOM Cooma - Snowy Mountains Airport Cooma NSW YCOR Corowa Airport Corowa NSW YCTM Cootamundra Airport Cootamundra NSW YCWR Cowra Airport Cowra NSW YDLQ Deniliquin Airport Deniliquin NSW YFBS Forbes Airport Forbes NSW YGFN Grafton Airport Grafton NSW YGLB Goulburn Airport Goulburn NSW YGLI Glen Innes Airport Glen Innes NSW YGTH Griffith Airport Griffith NSW YHAY Hay Airport Hay NSW YIVL Inverell Airport Inverell NSW YIVO Ivanhoe Aerodrome Ivanhoe NSW YKMP Kempsey Airport Kempsey NSW YLHI Lord Howe Island Airport Lord Howe Island NSW YLIS Lismore Regional Airport Lismore NSW YLRD Lightning Ridge Airport Lightning Ridge NSW YMAY Albury Airport Albury NSW YMDG Mudgee Airport Mudgee NSW YMER Merimbula -

2020 Master Plan
Alice Springs Airport 2020 Master Plan Preliminary Draft – Summary May 2020 The Alice Springs Airport 2020 Preliminary Draft Master Plan has been prepared with care based on information available at the time of writing. Please note that the content for this master plan was developed prior to the COVID-19 pandemic, and does not take account of the effect this may have on the business of Alice Springs Airport. This means that some of the content and/or timing of the plan may change as a result. 2 Alice Springs Airport 2020 Master Plan PRELIMINARY DRAFT – Summary Welcome I am proud to present the Alice Springs Airport 2020 Master Plan, which includes the Alice Springs Airport Environment Strategy. This important document outlines our vision for Alice Springs Airport over the next 20 years. Both a regulatory requirement and an important strategic planning tool, it is a blueprint for the airport’s development, painting a coherent picture of the airport’s operational, economic, commercial, social and environmental aspects that will guide our planning out to 2040. Alice Springs Airport has long been the gateway to the ‘Red Centre’ and welcomes some 620,000 passengers every year. Our close partnerships with the tourism industry, government, regulators and many other stakeholders help us connect Territory communities and provide essential facilities for the aviation and defence industries. Since privatisation in 1998, more than $80 million has been invested in Alice Springs Airport. This 2020 master plan covers the same core concepts as the previous four master plans. The updates mainly reflect the airport’s modest growth projections, its evolving airport business and the needs of our business partners. -

Global Evaluation of Biofuel Potential from Microalgae
Utah State University DigitalCommons@USU All Graduate Theses and Dissertations Graduate Studies 5-2014 Global Evaluation of Biofuel Potential from Microalgae Jeffrey W. Moody Utah State University Follow this and additional works at: https://digitalcommons.usu.edu/etd Part of the Mechanical Engineering Commons Recommended Citation Moody, Jeffrey W., "Global Evaluation of Biofuel Potential from Microalgae" (2014). All Graduate Theses and Dissertations. 2070. https://digitalcommons.usu.edu/etd/2070 This Thesis is brought to you for free and open access by the Graduate Studies at DigitalCommons@USU. It has been accepted for inclusion in All Graduate Theses and Dissertations by an authorized administrator of DigitalCommons@USU. For more information, please contact [email protected]. GLOBAL EVALUATION OF BIOFUEL POTENTIAL FROM MICROALGAE by Jeffrey W. Moody A thesis submitted in partial fulfillment of the requirements for the degree of MASTER OF SCIENCE in Mechanical Engineering Approved: Dr. Jason Quinn Dr. Byard Wood Major Professor Committee Member Dr. Rees Fullmer Dr. Mark McLellan Committee Member Vice President for Research and Dean of the School of Graduate Studies UTAH STATE UNIVERSITY Logan, Utah 2014 ii Copyright © Jeffrey Moody 2014 All Rights Reserved iii ABSTRACT Global Evaluation of Biofuel Potential from Microalgae by Jeffrey W. Moody, Master of Science Utah State University, 2014 Major Professor: Dr. Jason C. Quinn Department: Mechanical and Aerospace Engineering Traditional terrestrial crops are currently being utilized as a feedstock for biofuels but resource requirements and low yields limit the sustainability and scalability. Comparatively, next generation feedstocks, such as microalgae, have inherent advantages such as higher solar energy efficiencies, larger lipid fractions, utilization of waste carbon dioxide, and cultivation on poor quality land. -

AFP Darwin: a United Front >
Policing the Northern Territory Words: Rob Crispe, Marketing and Communications Comprising just one per cent of the Australian population are the residents of the Northern Territory, for whom there is no such thing as winter or big city noise. Contrasting world population data, there are more males than females in the Territory and the median age is just 30. However for the approximately 80 AFP members stationed in the NT, the uniqueness of the region does not end with its statistical facts. AFP Darwin: A united front h e AFP’s presence in Darwin is diverse and increasingly important to Australian law enforcement, security and defence. h e Darwin Offi ce — comprising personnel from the AFP and Northern Territory Police — is actively engaged Staff at Darwin Airport share the environment with all sorts of Australian fauna, including this in a variety of investigations and Northern Death Adder. operations spanning all crime types and Multicultural Aff airs, Customs, Darwin Offi ce Manager, Federal Agent including counter terrorism, fraud, Centrelink, Commonwealth DPP, Mick Calatzis, believes the cultivation of drug importation, organised people Australian Fisheries Management such cross-agency relationships is a key smuggling and protection. Authority, NT Police, Northern contributor in achieving success in the h e offi ce works closely with the Royal Command (NORCOMM), Australian region. h is includes strong links to the Australian Air Force, Royal Australian Security Intelligence Organisation, and AFP personnel at Darwin Airport, who Navy, Department of Immigration Coastwatch. operate under the direction of Airport > Platypus Magazine | Edition 92, September 2006 39 Below: Federal Agents David Perry, Sinead Done and David Williams.