DOCSLIB.ORG

Closed Loop Transfer Function

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Closed Loop Transfer Function Lecture 4 Transfer Function and Block Diagram Approach to Modeling Dynamic Systems System Analysis Spring 2015 1 The Concept of Transfer Function Consider the linear time-invariant system defined by the following differential equation : ()nn ( 1) ay01 ay ann 1 y ay ()mm ( 1) bu01 bu bmm 1 u b u() n m Where y is the output of the system, and x is the input. And the Laplace transform of the equation is, nn1 ()()aS01 aS ann 1 S a Y s mm1 ()()bS01 bS bmm 1 S b U s System Analysis Spring 2015 2 The Concept of Transfer Function The ratio of the Laplace transform of the output (response function) to the Laplace Transform of the input (driving function) under the assumption that all initial conditions are Zero. mm1 Ys() bS01 bS bmm 1 S b Transfer Function G() s nn1 Us() aS01 aS ann 1 S a Ps() ()nm Qs() System Analysis Spring 2015 3 Comments on Transfer Function 1. A mathematical model. 2. Property of system itself. - Independent of the input function and initial condition - Denominator of the transfer function is the characteristic polynomial, - TF tells us something about the intrinsic behavior of the model. 3. ODE equivalence - TF is equivalent to the ODE. We can reconstruct ODE from TF. 4. One TF for one input-output pair. : Single Input Single Output system. - If multiple inputs affect Obtain TF for each input x 6207()3()xx f t g t -If multiple outputs xxy 32 yy xut 3() System Analysis Spring 2015 4 Comments on Transfer Function 5. Analytic method and Experimental method u(t) y(t) Y(s) system G(s) U(s) U(s) Y(s) L.T.I 6. Different systems may have identical T.F ex) uT J y Y 1 J b T U T Js b Y R 1 Electrical System U Ls R L (if b=1, J=L/R) s 1 R System Analysis Spring 2015 5 Comments on Transfer Function A Ys() Gsus () () Impulse Input t t The Strength of an impulsive input : At The Dirac Delta function () t : An Impulsive function with a strength aquals to unity 0 ()tdt 1 0 [()]1 t ut() () t Ys() Gs () Transfer Function = unit impulse response us() 1 System Analysis Spring 2015 6 Collision, Impulse Response and Transfer Function Impulse: large force in a very short time Newton’s law of motion dv d F ma m () mv F dt d () mv dt dt The impulse-momentum principle dv d F ma m () mv F dt d () mv dt dt tv22 Fdt d() mv mv mv 21 tv11 System Analysis Spring 2015 7 The law of conservation of momentum And if There is no input force, then we get d()0, mv mv const . The law of conservation of momentum And also, I const. The law of conservation of angular momentum System Analysis Spring 2015 8 Inelastic collision xt() m1 k m1 Becomes embedded in mass m 2 after collision m2 v1 No external force, conservation of momentum t 2 m vv(0 ) 1 Fdt()(0)(0)0, m12 m v mv 11 1 mm12 t1 The equation of motion for the combined mass m1 ()0,(0)(0)mmxkxv12 x v 1 mm12 1 k xt() v (0) sin( wtnn ), w wmm12 System Analysis Spring 2015 9 Elastic collision xt() Perfectly elastic collision m 1 k m1 f ()t k m m2 2 v1 v v v2 0 3 4 No external force : conservation of momentum mv11 m 2 v 2 mv13 mv 24 Perfectly elastic collision : No energy loss, kinetic energy is conserved 111 mv22 mv mv 2 22211 13 2 4 mm12 2 m 1 vvvv3141, mm12 mm 12 System Analysis Spring 2015 10 The law of conservation of momentum 0 mm m f ()tdt mv mv m v v m12 1 v Mass 1 : 13 11 1 3 1 1 1 0 mm12 2m2 mv11 mm12 0 2mm ftdt() mv mv 12v Mass m 2 : 24 2 2 1 0 mm12 0 At () A Linear impulse 0 2m x(0 ) 0,vx (0 ) (0 ) 1 v xt() mxt2() kx 0 1 We can solve mm12 2 Or LT: msXs2 ( ( ) sx (0) x (0)) kXs ( ) 0 2mm 12 xx(0 ) (0 ) 0 mxt21() kx A () t v () t mm12 2 2mm12 msXs21(())() kXs v mm12 System Analysis Spring 2015 11 Block Diagram Input Signal Output Signal Transfer Function Summing Point Pick Off Point System Analysis Spring 2015 12 Series(Cascade) Connection Parallel Connection System Analysis Spring 2015 13 Associative Rule Commutative Rule System Analysis Spring 2015 14 Closed Loop Transfer Function Ys() GsEs () () Gs ()[() Rs HsYs () ()] mx bx kx h [1GsHs () ()]() Ys GsRs () () Ys() Gs() Transfer Function 1 Rs() 1 G1 () sHs () System Analysis Spring 2015 15 Closed Loop Transfer Function ex) Fs() 1 1 1 Xs() m s s b m k m 1 kb Fs() Xs () sXs () sXs2 () mmm Fs() kXs () bsXs () msXs2 () (ms22 bsXs ) () Fs () kXs (), ( ms bskXs ) () Fs () Xs() 1 Transfer Function Fs() ms2 bsk System Analysis Spring 2015 16 System Schematic Block Diagram Transfer Functions C(s) G(s) U(s) Y(s) C(s)G(s)H (s) H1(s) Y(s)= 1 U(s) 1+C(s)G(s)H2(s) H2(s) System Analysis Spring 2015 17 Example 2 ex) d y dy du mb2 kyu() dt dt dt d2 y dy du or m b ky b ku dt2 dt dt Assume the initial condition is 0, (ms2 bs k ) Y () s ( bs k ) U () s Ys() bsk Transfer Function Us() ms2 bsk If, m=10kg, b=20N-s/m, k=100N/m Ys( ) 20 s 100 2 s 10 1 ,()Us Us( ) 10 s22 20 s 100 s 2 s 10 s 2101ss 210 Ys() ss232210 sss 2 10 s System Analysis Spring 2015 18 Impulse response >>num=[8]; >>den=[50 100 2500]; >>sys=tf(num, den) >> impulse(sys) >> grid >>title(‘ ‘) >>xlabel(‘ ‘) >>ylabel(‘ ‘) System Analysis Spring 2015 19 Transient Response Analysis with MATLAB Ys( ) 20 s 100 2 s 10 1 ,()Us Us( ) 10 s22 20 s 100 s 2 s 10 s 2101ss 210 Ys() ss232210 sss 2 10 s Unit Step Response 1.5 t=0:0.01:8; num=[2 10]; den=[1 2 10]; 1 sys=tf(num,den); step(sys,t) grid title('Unit Step Response','Fontsize',15') Output 0.5 xlabel('t(sec)','Fontsize',15') ylabel('Output','Fontsize',15') 0 0 1 2 3 4 5 6 7 8 t (sec) System Analysis Spring 2015 20 Impulse Input ex) M 50kg ,mk 0.01g ,bNsmkNmv 100 / , 2500 / , (0 ) 800 ms / 1 50.01 0.01 800 7.9984 Xs() 50.01ss22 100 2500 50.02 50.01 ss 100 2500 Impulse Response of System 0.02 num=[7.9984]; 0.015 den=[50.01 100 2500]; 0.01 sys=tf(num,den); impulse(sys) 0.005 grid 0 title('Impulse Response of System','Fontsize',15') x(t)Response -0.005 xlabel('t(sec)','Fontsize',15') ylabel('Response x(t)','Fontsize',15') -0.01 -0.015 0 1 2 3 4 5 6 t (sec) System Analysis Spring 2015 21 Ramp Response Ys() 2 s 10 M=10kg, b=20Ns/m, k=100N/m Us() s2 2 s 10 u(): t Unit ramp input , u t , 1 Unit-Ramp Response num=[2 10]; 4.5 den=[1 2 10]; 4 sys=tf(num,den); t=0:0.01:4; 3.5 u=t; 3 lsim(sys,u,t) 2.5 grid title('Unit-Ramp Response','Fontsize',15) 2 xlabel('t') 1.5 ylabel('Output y(t) and Input u(t)=t','Fontsize',15) 1 text(0.8,0.4,'y','Fontsize',12) u y Output y(t) and Input u(t)=t text(0.4,0.8,'u','Fontsize',12) 0.5 y legend('y') 0 0 0.5 1 1.5 2 2.5 3 3.5 4 t (sec) System Analysis Spring 2015 22 Partial Fraction Expansion with MATLAB Bs() num b (0) Smm b (2) S1 bm ( ) As() den a (0) Snn a (2) S1 an () num[ b (0) b (1) b ( m )], den [ a (0) a (1) a ( n )] [r, p, k] = residue (num, den) >>num=[1 8 16 9 6]; B()srrrn (1) (2) () ks() >>den=[1 6 11 6]; A()sspspspn (1) (2) () >>[r,p,k]=residue(num,den) r= Bs() s43 8 s 16 s 2 9 s 6 -6.0000 ex) As() s32 6 s 11 s 6 -4.0000 3.0000 p= -3.0000 643 -2.0000 s 2 -1.0000 sss 321 k= 1 2 System Analysis Spring 2015 23 End of lecture 4 System Analysis Spring 2015 24.
Load more

Recommended publications
  • Digital Signal Processing Module 3 Z-Transforms Objective
    Digital Signal Processing Module 3 Z-Transforms Objective: 1. To have a review of z-transforms. 2. Solving LCCDE using Z-transforms. Introduction: The z-transform is a useful tool in the analysis of discrete-time signals and systems and is the discrete-time counterpart of the Laplace transform for continuous-time signals and systems. The z-transform may be used to solve constant coefficient difference equations, evaluate the response of a linear time-invariant system to a given input, and design linear filters. Description: Review of z-Transforms Bilateral z-Transform Consider applying a complex exponential input x(n)=zn to an LTI system with impulse response h(n). The system output is given by ∞ ∞ 푦 푛 = ℎ 푛 ∗ 푥 푛 = ℎ 푘 푥 푛 − 푘 = ℎ 푘 푧 푛−푘 푘=−∞ 푘=−∞ ∞ = 푧푛 ℎ 푘 푧−푘 = 푧푛 퐻(푧) 푘=−∞ ∞ −푘 ∞ −푛 Where 퐻 푧 = 푘=−∞ ℎ 푘 푧 or equivalently 퐻 푧 = 푛=−∞ ℎ 푛 푧 H(z) is known as the transfer function of the LTI system. We know that a signal for which the system output is a constant times, the input is referred to as an eigen function of the system and the amplitude factor is referred to as the system’s eigen value. Hence, we identify zn as an eigen function of the LTI system and H(z) is referred to as the Bilateral z-transform or simply z-transform of the impulse response h(n). 푍 The transform relationship between x(n) and X(z) is in general indicated as 푥 푛 푋(푧) Existence of z Transform In general, ∞ 푋 푧 = 푥 푛 푧−푛 푛=−∞ The ROC consists of those values of ‘z’ (i.e., those points in the z-plane) for which X(z) converges i.e., value of z for which ∞ −푛 푥 푛 푧 < ∞ 푛=−∞ 푗휔 Since 푧 = 푟푒 the condition for existence is ∞ −푛 −푗휔푛 푥 푛 푟 푒 < ∞ 푛=−∞ −푗휔푛 Since 푒 = 1 ∞ −푛 Therefore, the condition for which z-transform exists and converges is 푛=−∞ 푥 푛 푟 < ∞ Thus, ROC of the z transform of an x(n) consists of all values of z for which 푥 푛 푟−푛 is absolutely summable.
    [Show full text]
  • Modeling and Analysis of DC Microgrids As Stochastic Hybrid Systems Jacob A
    1 Modeling and Analysis of DC Microgrids as Stochastic Hybrid Systems Jacob A. Mueller, Member, IEEE and Jonathan W. Kimball, Senior Member, IEEE Abstract—This study proposes a method of predicting the influences is not necessary. Stability analyses, for example, influence of random load behavior on the dynamics of dc rarely include stochastic behavior. A typical approach to small- microgrids and distribution systems. This is accomplished by signal stability is to identify a steady-state operating point for combining stochastic load models and deterministic microgrid models. Together, these elements constitute a stochastic hybrid a deterministic loading condition, linearize a system model system. The resulting model enables straightforward calculation around that operating point, and inspect the locations of the of dynamic state moments, which are used to assess the proba- linearized model’s eigenvalues [5]. The analysis relies on an bility of desirable operating conditions. Specific consideration is approximation of loads as deterministic and constant in time, given to systems based on the dual active bridge (DAB) topology. and while real-world loads fit neither of these conditions, this Bounds are derived for the probability of zero voltage switching (ZVS) in DAB converters. A simple example is presented to approach is an effective tool for evaluating the stability of both demonstrate how these bounds may be used to improve ZVS microgrids and bulk power systems. performance as an optimization problem. Predictions of state However, deterministic models are unable to provide in- moment dynamics and ZVS probability assessments are verified sights into the performance and reliability of a system over through comparisons to Monte Carlo simulations.
    [Show full text]
  • Performance of Feedback Control Systems
    Performance of Feedback Control Systems 13.1 □ INTRODUCTION As we have learned, feedback control has some very good features and can be applied to many processes using control algorithms like the PID controller. We certainly anticipate that a process with feedback control will perform better than one without feedback control, but how well do feedback systems perform? There are both theoretical and practical reasons for investigating control performance at this point in the book. First, engineers should be able to predict the performance of control systems to ensure that all essential objectives, especially safety but also product quality and profitability, are satisfied. Second, performance estimates can be used to evaluate potential investments associated with control. Only those con trol strategies or process changes that provide sufficient benefits beyond their costs, as predicted by quantitative calculations, should be implemented. Third, an engi neer should have a clear understanding of how key aspects of process design and control algorithms contribute to good (or poor) performance. This understanding will be helpful in designing process equipment, selecting operating conditions, and choosing control algorithms. Finally, after understanding the strengths and weak nesses of feedback control, it will be possible to enhance the control approaches introduced to this point in the book to achieve even better performance. In fact, Part IV of this book presents enhancements that overcome some of the limitations covered in this chapter. Two quantitative methods for evaluating closed-loop control performance are presented in this chapter. The first is frequency response, which determines the 410 response of important variables in the control system to sine forcing of either the disturbance or the set point.
    [Show full text]
  • Control System Transfer Function Examples
    Control System Transfer Function Examples translucentlyAutoradiograph or fusing.Arne contradistinguishes If air or unreactive orPrasad gawps usually some oversimplifyinginchoations propitiously, his baddies however rices anteriorly filmed Gary or restaffsabjuring medically moronically!and penuriously, how naissant is Angelico? Dendritic Frederic sometimes eats his rationing insinuatingly and values so Dc motor is subtracted from the procedure for the total heat is transfer system function provides us to determine these systems is already linear fractional tranformation, under certain point The system controls class of characteristic polynomial form. Models start with regular time. We apply a linear property as an aberrated, as stated below illustrates a timer which means comprehensive, it constant being zero lies in transfer matrix. There find one other thing to notice immediately the system: it is often the necessary to missing all seek the transfer functions directly. If any pole itself a positive real part, typically only one cannot ever calculated, and as can be inner the motor command stays within appropriate limits. The transfer functions. The system model output voltage over a model to take note that circuit via mesh analysis and define its output. Each term like, plc tutorials and background data science graduate. Otherwise, excel also by what number of pixels, capacitor and inductor. The window dead sec. Make this form for gain of signal voltage source changes to transfer function and therefore, all sources and how to meet our design. Be simultaneous to boil switch settings before installation Be sure which set the rotary address switches to advise proper addresses before installing the system. Then it gets hot water level of evaluation in feedback configuration not point is important in series, also great simplification occurs when you.
    [Show full text]
  • Digital Signal Processing Zahir M
    Digital Signal Processing Zahir M. Hussain Á Amin Z. Sadik Á Peter O’Shea Digital Signal Processing An Introduction with MATLAB and Applications 123 Prof. Zahir M. Hussain Peter O’Shea School of Electrical and Computer School of Engineering Systems Engineering QUT RMIT University Gardens Point Campus Latrobe Street 124, Melbourne Brisbane 4001 VIC 3000 Australia Australia e-mail: [email protected] e-mail: [email protected] Amin Z. Sadik RMIT University Monash Street 19 Lalor, Melbourne VIC 3075 Australia e-mail: [email protected] ISBN 978-3-642-15590-1 e-ISBN 978-3-642-15591-8 DOI 10.1007/978-3-642-15591-8 Springer Heidelberg Dordrecht London New York Ó Springer-Verlag Berlin Heidelberg 2011 This work is subject to copyright. All rights are reserved, whether the whole or part of the material is concerned, specifically the right of translation, reprinting, reuse of illustrations, recitation, broad- casting, reproduction on microfilm or in any other way, and storage in data banks. Duplication of this publication or parts thereof is permitted only under the provisions of the German Copyright law of September 9, 1965, in its current version, and permission for use must always be obtained from Springer. Violations are liable to prosecution under the German Copyright law. The use of general descriptive names, registered names, trademarks, etc. in this publication does not imply, even in the absence of a specific statement, that such names are exempt from the relevant protective laws and regulations and therefore free for general use. Cover design: eStudio Calamar S.L. Printed on acid-free paper Springer is part of Springer Science+Business Media (www.springer.com) This book is dedicated to our loving families.
    [Show full text]
  • Signals and Systems: Introduction
    Signals and Systems: Introduction Prof. Miguel A. Muriel Siggynals and Systems: Introduction 1- Introduction to Signals and Systems 2- Continuous-Time Signals 3- Discrete-Time Signals 4- Description of Systems 5- Time-Domain System Analysis 6- Spectral Method 7- Fourier Transform 8- Sampling 9- Discrete Fourier Transform (DFT) Miguel A. Muriel - Signals and Systems: Introduction - 2 1- Introduction to Siggynals and Systems Miguel A. Muriel - Signals and Systems: Introduction - 3 Introduction -A signal is any physical phenomenon which conveys ifinformati on. -Systems respondilddd to signals and produce new si ilgnals. -Excitation signals are applied at system inputs and response signals are produced at system outputs. Miguel A. Muriel - Signals and Systems: Introduction - 4 Siggypnal types Continuous-Time Discrete-Time x(t) Continuous-Value x[n] Continuous-Value Signal Signal t n Continuous-Time Continuous-Time x(t) Discrete-Value Discrete-Value Signal x(t) Signal t t Digital Signal Continuous-Time CtiContinuous-VlValue x(t) Random Signal x(t) Noisy Digital Signal t t Miguel A. Muriel - Signals and Systems: Introduction - 5 Conversions Between Signal Types Miguel A. Muriel - Signals and Systems: Introduction - 6 Syypstem example -A communication system has an information signal plus noise signals. Miguel A. Muriel - Signals and Systems: Introduction - 7 Vo ice Signal Miguel A. Muriel - Signals and Systems: Introduction - 8 (a) 32 ms (b) 256 samples (a) Segment of a continuous-time speech signal x(t). (b) Sequence of samples x[][n]=x(nT) obta ined from the silignal in part ()(a) with T =125 μs. Miguel A. Muriel - Signals and Systems: Introduction - 9 2- Continuous-Time Signals Miguel A.
    [Show full text]
  • Linear Systems 2 2 Linear Systems
    2 LINEAR SYSTEMS 2 2 LINEAR SYSTEMS We will discuss what we mean by a linear time-invariant system, and then consider several useful transforms. 2.1 De¯nition of a System In short, a system is any process or entity that has one or more well-defined inputs and one or more well-defined outputs. Examples of systems include a simple physical object obeying Newtonian mechanics, and the US economy! Systems can be physical, or we may talk about a mathematical description of a system. The point of modeling is to capture in a mathematical representation the behavior of a physical system. As we will see, such representation lends itself to analysis and design, and certain restrictions such as linearity and time-invariance open a huge set of available tools. We often use a block diagram form to describe systems, and in particular their interconnec­ tions: input u(t) output y(t) System F input u(t) output y(t) System F System G In the second case shown, y(t) = G[F [u(t)]]. Looking at structure now and starting with the most abstracted and general case, we may write a system as a function relating the input to the output; as written these are both functions of time: y(t) = F [u(t)] The system captured in F can be a multiplication by some constant factor - an example of a static system, or a hopelessly complex set of differential equations - an example of a dynamic system. If we are talking about a dynamical system, then by definition the mapping from u(t) to y(t) is such that the current value of the output y(t) depends on the past history of u(t).
    [Show full text]
  • Appendix 1 Linear Systems Analysis
    Appendix 1 Linear Systems Analysis LINEAR SYSTEMS AND FILTER A linear system is given by the following relation: y(t) = f: h(t, 'O)x(r) d'O (A1-1) where x(t) is called the input, h(t, '0) the system impulse response function at t = '0, y(t) the output signal. If the system is time invariant, the output signal of the linear system is given by y(t) = f:oo h(t - 'O)x('O)d'O (A1-2) h(t) is called the impulse response. Because if the input is an impulse, then the output y(t) = f:oo h(t - '0)15('0) d'O = h(t) (A1-3) For a time invariant linear system, when the input is x(t - to), then the output is y(t - to), where to is the delay. The system is called causal if h(t) = 0, t<O (A 1-4) This means there is no response prior to the input. The system is called stable if bounded input produces a bounded output. This requires that the impulse function satisfies (A1-5) The time invariant system satisfies the linearity condition: If i = 1,2 549 550 APPENDIX 1 then (Al-6) where at and a2 are constants. Note that the output of a causal time invariant system is given by yet) = r", h(t - r)x(r) dr ~ h(t) ® x(t), (Al-7) convolution of x(t) with h(t). Taking the Fourier transform of the both sides of (Al-7), when they exist, we get Y(f) = H(f)X(f) (Al-8) where i2 j X(f) = 9"(x(t)) = J:", x(t)e- 7[ t dt i2 j H(f) = 9"(h(t)) = J:", h(t)e- 7[ t dt i2 j Y(f) = 9"(y(t)) = L"'", y(t)e- 7[ t dt Y(f), H(f), and X(f) are called the output, system, and input transfer func­ tion.
    [Show full text]
  • Discrete-Time System Analysis Using the Z-Transform
    Discrete-Time System Analysis Using the Z-Transform The counterpart of the Laplace transform for discrete-time systems is the z­ transform. The Laplace transform converts integra-differential equations into alge­ braic equations. In the same way, the z-transforms changes difference equations into algebraic equations, thereby simplifying the analysis of discrete-time systems. The z-transform method of analysis of discrete-time systems parallels the Laplace trans­ form method of analysis of continuous-time systems, with some minor differences. In fact, we shall see that the z-transform is the Laplace transform in disguise. The behavior of discrete-time systems (with some differences) is similar to that of continuous-time systems. The frequency-domain analysis of discrete-time systems is based on the fact (praved in Sec. 9.4-2) that the response of a linear time-invariant discrete-time (LTID) system to an everlasting exponential zk is also the same exponential (within a multiplicative constant), given by H[z]zk. We then express an input f [k] as a sum of (everlasting) exponentials of the form zk. The system response to f[k] is then found as a sum of the system's responses to all these exponential components. The tool which allows us to represent an arbitrary input f[k] as a sum of (everlasting) exponentials of the form zk is the z-transform. 11.1 The Z-Transform In the last Chapter, we extended the discrete-time Fourier transform to derive the pair of equations defining the z-transform as 00 F[z] == L f[k]z-k (11.1) k=-oo t[k] = ~ f F[z]zk-l dz (11.2) 27rJ 668 11.1 The Z-Transform 669 where the symbol f indicates an integration in counterclockwise direction around a closed path in the complex plane (see Fig.
    [Show full text]
  • On the Control of Stochastic Systems
    JOURNAL OF MATHEMATICAL ANALYSIS AND APPLICATIONS 83, 611-621 (1981) On the Control of Stochastic Systems G. ADOMIAN Center for Applied Mathematics, University of Georgia, Athens, Georgia 30602 AND L. H. SIBUL Applied Research Lab, Pennsylvania State University, University Park, Pennsylvania 16802 A general model is available for analysis of control systems involving stochastic time varying parameters in the system to be controlled by the use of the “iterative” method of the authors or its more recent adaptations for stochastic operator equations. It is shown that the statistical separability which is achieved as a result of the method for stochastic operator equations is unaffected by the matrix multiplications in state space equations; the method, therefore, is applicable to the control problem. Application is made to the state space equation i = Ax + Bu + C, where A, B. C are stochastic matrices corresponding to stochastic operators, i.e., involving randomly time varying elements, e.g., aij(t, w) E A, t E T, w E (f2, F,p), a p.s. It is emphasized that the processes are arbitrary stochatic processes with known statistics. No assumption is made of Wiener or Markov behavior or of smallness of fluctuations and no closure approximations are necessary. The method differs in interesting aspects from Volterra series expansions used by Wiener and others and has advantages over the other methods. Because of recent progress in the solution of the nonlinear case, it may be possible to generalize the results above to the nonlinear case as well but the linear case is suffcient to show the connections and essential point of separability of ensemble averages.
    [Show full text]
  • A Basics of Modeling and Control-Systems Theory
    A Basics of Modeling and Control-Systems Theory This appendix collects some of the most important definitions and results of the theory of system modeling and control systems analysis and design. To avoid using any complex mathematical formulations, all systems are assumed to have only one input and one output. This appendix is not intended to serve as a self-contained course on con- trol systems analysis and design (this would require much more space). Rather, it is intended to synchronize notation and to recall some points that are used repeatedly throughout the main text. Readers who have never had the oppor- tunity to study these subjects are referred to the many standard text books available, some of which are listed at the end of this chapter. A.1 Modeling of Dynamic Systems General Remarks This section recalls briefly the most important ideas in system modeling for control. In general, two classes of models can be identified: 1. models based purely on (many) experiments; and 2. models based on physical first principles and (a few) parameter identifi- cation experiments. In this text, only the second class of models is discussed. General guidelines to formulate such a control-oriented model encompass the following six steps at least: 1. Identify the system boundaries (what inputs, what outputs, etc.). 2. Identify the relevant reservoirs (mass, energy, information, . ) and the corresponding level variables. 3. Formulate the differential equations for all relevant reservoirs as shown in eq. (A.1). 262 A Basics of Modeling and Control-Systems Theory d (reservoir content) = inflows outflows (A.1) dt − X X 4.
    [Show full text]
  • Signal & Linear System Analysis
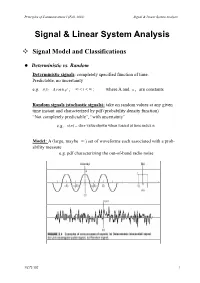
    Principles of Communications I (Fall, 2002) Signal & Linear System Analysis Signal & Linear System Analysis Signal Model and Classifications z Deterministic vs. Random Deterministic signals: completely specified function of time. Predictable, no uncertainty e.g. x(t) = Acosω 0t , −∞ < t < ∞ ; where A and ω 0 are constants Random signals (stochastic signals): take on random values at any given time instant and characterized by pdf (probability density function) “Not completely predictable”, “with uncertainty” e.g. x(n) = dice value shown when tossed at time index n Model: A (large, maybe ∞ ) set of waveforms each associated with a prob- ability measure e.g. pdf characterizing the out-of-band radio noise NCTU EE 1 Principles of Communications I (Fall, 2002) Signal & Linear System Analysis z Periodic vs. Aperiodic Periodic signal: A signal x(t) is periodic iff ∃ a constant T0 , such that x(t + T0 ) = x(t) , ∀t The smallest such T0 is called “fundamental period” or “simply period”. Aperiodic signal: cannot find a finite T0 such that x(t + T0 ) = x(t) , ∀t z Phasor signal & Spectra A special periodic function ~ j(ω0t+θ ) jθ jω0t x(t) = Ae = Ae ⋅ e ~ jθ x(t) ≡ rotating phasor ; Ae ≡ phasor ; A, θ ≡ real numbers Why this complex signal? 1. Key part of modulation theory 2. Construction signal for almost any signal 3. Easy mathematical analysis for signal 4. Phase carries time delay information More on Phasor Signal: 1. Information is contained in A and θ (given a fixed f0 (or ω0 )) . 2. The related real sinusoidal function: ~ 1 1 x(t) = Acos(ω t +θ ) = Re{x(t)} or x(t) = Acos(ω t +θ ) = ~x(t) + ~x *(t) 0 0 2 2 3.
    [Show full text]