Are Retail Investors Less Aggressive on Small Price Stocks?
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Content Requirements Checklist for Information Document
CONTENT REQUIREMENTS CHECKLIST FOR INFORMATION DOCUMENT ADMISSION TO TRADING OF SHARES ON EURONEXT GROWTH OPERATED BY OSLO BØRS CONTENT REQUIREMENTS CHECKLIST FOR INFORMATION DOCUMENT No. Description of requirement Reference to section(s) in the information document 2.1 General information to be included in the Information Document1 The following disclaimer shall be put on the first page of the Information Document: “Euronext Growth is a market operated by Euronext. Companies on Euronext Growth, a multilateral trading facility (MTF), are not subject to the same rules as companies on a Regulated Market (a main market). Instead they are subject to a less extensive set of rules and regulations adjusted to small growth companies. The risk in investing in a company on Euronext Growth may therefore be higher than investing in a company on a Regulated Market. Investors should take this into account when making investment decisions.” The following statement shall be put on the first page of the Information Document: “The present Information Document does not constitute a prospectus within the meaning of Regulation (EU) 2017/1129 of the European Parliament and of the Council of 14 June 2017 on the prospectus to be published when securities are offered to the public or admitted to trading on a regulated market, and repealing Directive 2003/71. The present Information Document has been drawn up under the responsibility of the Issuer. It has been reviewed by the Euronext Growth Advisor and has been subject to an appropriate review of its completeness, consistency and comprehensibility by Euronext.” The following liability statement from the persons responsible 2for the Information Document shall be included in the Information Document: 1 Cf. -
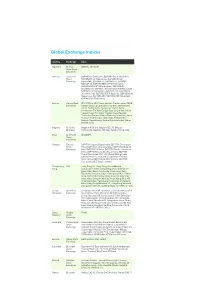
Global Exchange Indices
Global Exchange Indices Country Exchange Index Argentina Buenos MERVAL, BURCAP Aires Stock Exchange Australia Australian S&P/ASX All Ordinaries, S&P/ASX Small Ordinaries, Stock S&P/ASX Small Resources, S&P/ASX Small Exchange Industriials, S&P/ASX 20, S&P/ASX 50, S&P/ASX MIDCAP 50, S&P/ASX MIDCAP 50 Resources, S&P/ASX MIDCAP 50 Industrials, S&P/ASX All Australian 50, S&P/ASX 100, S&P/ASX 100 Resources, S&P/ASX 100 Industrials, S&P/ASX 200, S&P/ASX All Australian 200, S&P/ASX 200 Industrials, S&P/ASX 200 Resources, S&P/ASX 300, S&P/ASX 300 Industrials, S&P/ASX 300 Resources Austria Vienna Stock ATX, ATX Five, ATX Prime, Austrian Traded Index, CECE Exchange Overall Index, CECExt Index, Chinese Traded Index, Czech Traded Index, Hungarian Traded Index, Immobilien ATX, New Europe Blue Chip Index, Polish Traded Index, Romanian Traded Index, Russian Depository Extended Index, Russian Depository Index, Russian Traded Index, SE Europe Traded Index, Serbian Traded Index, Vienna Dynamic Index, Weiner Boerse Index Belgium Euronext Belgium All Share, Belgium BEL20, Belgium Brussels Continuous, Belgium Mid Cap, Belgium Small Cap Brazil Sao Paulo IBOVESPA Stock Exchange Canada Toronto S&P/TSX Capped Equity Index, S&P/TSX Completion Stock Index, S&P/TSX Composite Index, S&P/TSX Equity 60 Exchange Index S&P/TSX 60 Index, S&P/TSX Equity Completion Index, S&P/TSX Equity SmallCap Index, S&P/TSX Global Gold Index, S&P/TSX Global Mining Index, S&P/TSX Income Trust Index, S&P/TSX Preferred Share Index, S&P/TSX SmallCap Index, S&P/TSX Composite GICS Sector Indexes -

Execution Venues List
Execution Venues List This list should be read in conjunction with the Best Execution policy for Credit Suisse AG (excluding branches and subsidiaries), Credit Suisse (Switzerland) Ltd, Credit Suisse (Luxembourg) S.A, Credit Suisse (Luxembourg) S.A. Zweigniederlassung Österreichand, Neue Aargauer Bank AG published at www.credit-suisse.com/MiFID and https://www.credit-suisse.com/lu/en/private-banking/best-execution.html The Execution Venues1) shown enable the in scope legal entities to obtain on a consistent basis the best possible result for the execution of client orders. Accordingly, where the in scope legal entities may place significant reliance on these Execution Venues. Equity Cash & Exchange Traded Funds Country/Liquidity Pool Execution Venue1) Name MIC Code2) Regulated Markets & 3rd party exchanges Europe Austria Wiener Börse – Official Market WBAH Austria Wiener Börse – Securities Exchange XVIE Austria Wiener Börse XWBO Austria Wiener Börse Dritter Markt WBDM Belgium Euronext Brussels XBRU Belgium Euronext Growth Brussels ALXB Czech Republic Prague Stock Exchange XPRA Cyprus Cyprus Stock Exchange XCYS Denmark NASDAQ Copenhagen XCSE Estonia NASDAQ Tallinn XTAL Finland NASDAQ Helsinki XHEL France EURONEXT Paris XPAR France EURONEXT Growth Paris ALXP Germany Börse Berlin XBER Germany Börse Berlin – Equiduct Trading XEQT Germany Deutsche Börse XFRA Germany Börse Frankfurt Warrants XSCO Germany Börse Hamburg XHAM Germany Börse Düsseldorf XDUS Germany Börse München XMUN Germany Börse Stuttgart XSTU Germany Hannover Stock Exchange XHAN -

Press Release Paris – June 21St, 2021
Press Release Paris – June 21st, 2021 Europcar Mobility Group rejoins Euronext SBF 120 index Europcar Mobility Group, a major player in mobility markets, is pleased to announce that it has re-entered into the SBF 120 and CAC Mid 60 indices, in accordance with the decision taken by the Euronext Index Steering Committee. This re-entry, which took place after market close on Friday 18 June 2021, is effective from Monday 21 June 2021. The SBF 120 is one of the flagship indices of the Paris Stock Exchange. It includes the first 120 stocks listed on Euronext Paris in terms of liquidity and market capitalization. The CAC Mid 60 index includes 60 companies of national and European importance. It represents the 60 largest French equities beyond the CAC 40 and the CAC Next 20. It includes the 60 most liquid stocks listed in Paris among the 200 first French capitalizations. This total of 120 companies compose the SBF 120. Caroline Parot, CEO of Europcar Mobility Group, said: “Europcar Mobility Group welcomes the re-integration of the SBF 120 and CAC Mid 60. This follows the successful closing of the Group’s financial restructuring during Q1 2021, which allowed the Group to open a new chapter in its history. Europcar Mobility Group re-entry into the SBF 120 and CAC Mid 60 is an important step for our Group and recognizes the fact that we are clearly "back in the game”, in a good position to take full advantage of the progressive recovery of the Travel and Leisure market. In that perspective, our teams are fully mobilized for summer of 2021, in order to meet the demand and expectations of customers who are more than ever eager to travel”. -

Paris, Le 26 Mars 2001
PR/14/12 Eutelsat Communications joins CAC Large 60 index from 19 March 2012 Paris, March 2, 2012 - Eutelsat Communications (Euronext Paris: ETL) will join the CAC Next 20 and CAC Large 60 indices of NYSE Euronext Paris after the trading session of Monday 19 March 2012, at which point it will be withdrawn from the CAC Mid 60 and CAC Mid & Small indices. Following this, Eutelsat Communications will be part of the following indices of NYSE Euronext Paris: - CAC Next 20 - CAC Large 60 - SBF 120 - CAC All Shares - CAC All-Tradable - CAC Consumer Serv. - CAC Media The decision of the Scientific Board of Euronext Indices of 1 March 2012 enables Eutelsat to increase its visibility in the French and international financial community. Financial calendar The financial calendar below is provided for information purposes only. It is subject to change and will be regularly updated. - May 10, 2012: financial report for third quarter ended March 31, 2012 - July 30, 2012: earnings for full year ended June 30, 2012 - October 25, 2012: financial report for first quarter ended September 30, 2012 - November 8, 2012: Annual General Shareholders Meeting About Eutelsat Communications Eutelsat Communications (Euronext Paris: ETL, ISIN code: FR0010221234) is the holding company of Eutelsat S.A.. With capacity commercialised on 28 satellites that provide coverage over the entire European continent, as well as the Middle East, Africa, India and significant parts of Asia and the Americas, Eutelsat is one of the world's three leading satellite operators in terms of revenues. As of 31 December 2011, Eutelsat’s satellites were broadcasting more than 4,150 television channels. -

EURONEXT GROWTH MARKETS RULE BOOK Part II: Additional Rules for the Euronext Growth Market Operated by Euronext Dublin
EURONEXT GROWTH MARKETS RULE BOOK Part II: Additional rules for the Euronext Growth Market operated by Euronext Dublin ISSUE DATE: 9TH NOVEMBER 2020 EFFECTIVE DATE: 30 NOVEMBER 2020 TABLE OF CONTENTS Definitions ...................................................................................................................................................................... 3 1. Conditions for Admission to the Euronext Growth Market operated by Euronext Dublin .................................... 8 SPECIAL CONDITIONS FOR CERTAIN APPLICANTS .......................................................................................................... 8 2. Lock-ins for new businesses ................................................................................................................................... 8 3. Investing companies ............................................................................................................................................... 9 APPLICATION PROCEDURE ........................................................................................................................................... 10 4. Pre-admission announcement ............................................................................................................................. 10 5. Information document ......................................................................................................................................... 10 6. Further information documents ......................................................................................................................... -

Eurofins Fact Sheet March 2021
FACT SHEET Company Overview Our Vision: To be the Global Leader in Eurofins is Testing for Life. Eurofins is the global leader in food, environment, pharmaceutical and Testing for Life cosmetic product testing and in agroscience Contract Research services. Eurofins is also one of the market leaders in certain testing and laboratory services for genomics, discovery pharmacology, Our Mission: To contribute to a safer and forensics, advanced material sciences and in the support of clinical studies, as well as having an healthier world by providing our customers emerging global presence as a Contract Development and Manufacturing Organisation. The Group with innovative and high quality laboratory, also has a rapidly developing presence in highly specialised and molecular clinical diagnostic testing research and advisory services, whilst and in-vitro diagnostic products. creating opportunities for our employees and generating sustainable shareholder value History Eurofins Scientific was founded in 1987 with four employees to market the SNIF-NMR technology, Our Values: Customer Focus, Quality, a patented analytical method used to verify the origin and purity of several types of food and Competence & Team Spirit and Integrity beverages and identify sophisticated fraud not detectable by other methods. Today, the Eurofins Group is a leading provider of testing and analytical services with: • an international network of more than 800 laboratories in over 50 countries Revenues in EUR million • over 50,000 staff • a portfolio of over 200,000 analytical methods • more than 450 million tests performed each year Eurofins has been one of the fastest growing listed European companies. Since its IPO on the French stock exchange in 1997, Eurofins’ revenues have increased by 34% each year (in compound average) to over EUR 5.4 billion in 2020. -

Information Document Euronext Growth
INFORMATION DOCUMENT EURONEXT GROWTH FEBRUARY 21st, 2020 Facephi.com: EURONEXT Growth 3 FacePhi Facephi Biometría, S.A. C/ México, 20 Edificio Marsamar, 3ºC (03008) Alincante-SPAIN “Registro Mercantil de Alicante al número:” A- 54659313 Hereinafter “FacePhi” or “The Company” INFORMATION DOCUMENT EURONEXT GROWTH PARIS DIRECT ADMISSION TO NEGOTIATION ADVERTISSEMENT Euronext Growth is a market operated by Euronext. Companies on Euronext Growth are not subject to the same rules as companies on a Regulated Market (a main market). Instead they are subject to a less extensive set of rules and regulations adjusted to small growth companies. The risk in investing in a company on Euronext Growth may therefore be higher than investing in a company on a Regulated Market. The present Information Document does not constitute a prospectus within the meaning of Regulation (EU) 2017/1129 of the European Parliament abd of the Council of 14 of June 2017 on the prospectus to be published when securities are offered to the public or admitted to trading on a regulated market, and repealing Directive 2003/71. The present Information Document has been drawn up under the responsibility of FACEPHI. It has been reviewed by PMS, Asesores Registrados, S.L. and has been subject to an appropriate review of its completeness, consistency and comprehensibility by Euronext. We declare that, to the best of our knowledge, the information provided in this Information Document is accurate and that, to the best of our knowledge this Information Document is not subject to any (material) omissions, and that all relevant information is included in this Information Document. -

Financial Market Data for R/Rmetrics
Financial Market Data for R/Rmetrics Diethelm Würtz Andrew Ellis Yohan Chalabi Rmetrics Association & Finance Online R/Rmetrics eBook Series R/Rmetrics eBooks is a series of electronic books and user guides aimed at students and practitioner who use R/Rmetrics to analyze financial markets. A Discussion of Time Series Objects for R in Finance (2009) Diethelm Würtz, Yohan Chalabi, Andrew Ellis R/Rmetrics Meielisalp 2009 Proceedings of the Meielisalp Workshop 2011 Editor Diethelm Würtz Basic R for Finance (2010), Diethelm Würtz, Yohan Chalabi, Longhow Lam, Andrew Ellis Chronological Objects with Rmetrics (2010), Diethelm Würtz, Yohan Chalabi, Andrew Ellis Portfolio Optimization with R/Rmetrics (2010), Diethelm Würtz, William Chen, Yohan Chalabi, Andrew Ellis Financial Market Data for R/Rmetrics (2010) Diethelm W?rtz, Andrew Ellis, Yohan Chalabi Indian Financial Market Data for R/Rmetrics (2010) Diethelm Würtz, Mahendra Mehta, Andrew Ellis, Yohan Chalabi Asian Option Pricing with R/Rmetrics (2010) Diethelm Würtz R/Rmetrics Singapore 2010 Proceedings of the Singapore Workshop 2010 Editors Diethelm Würtz, Mahendra Mehta, David Scott, Juri Hinz R/Rmetrics Meielisalp 2011 Proceedings of the Meielisalp Summer School and Workshop 2011 Editor Diethelm Würtz III tinn-R Editor (2010) José Cláudio Faria, Philippe Grosjean, Enio Galinkin Jelihovschi and Ri- cardo Pietrobon R/Rmetrics Meielisalp 2011 Proceedings of the Meielisalp Summer Scholl and Workshop 2011 Editor Diethelm Würtz R/Rmetrics Meielisalp 2012 Proceedings of the Meielisalp Summer Scholl and Workshop 2012 Editor Diethelm Würtz Topics in Empirical Finance with R and Rmetrics (2013), Patrick Hénaff FINANCIAL MARKET DATA FOR R/RMETRICS DIETHELM WÜRTZ ANDREW ELLIS YOHAN CHALABI RMETRICS ASSOCIATION &FINANCE ONLINE Series Editors: Prof. -

Pixium Vision Announces a Financing Agreement for a Maximum Amount of €10 Million, Issuing a First Tranche of € 1.25 Million, for the Development of Its Prima System
PRESS RELEASE Pixium Vision announces a financing agreement for a maximum amount of €10 million, issuing a first tranche of € 1.25 million, for the development of its Prima system • Financing of the development of the Prima system on the back of its excellent clinical results • Subsequent drawdowns possible depending on financing needs • Subsequent drawdowns conditional to approval of needed resolutions at the AGM to be held on December 12, 2019 Paris, 6 November 2019 – 7.00 am CEST– Pixium Vision (FR0011950641 - PIX), a bioelectronics company that develops innovative bionic vision systems to enable patients who have lost their sight to live more independently, announces that it has concluded a financing agreement with the US-based investor, specialized in healthcare, European Select Growth Opportunities Fund (the “Investor”) for an issue of bonds repayable in cash and/or new shares (the “Bonds”) for a maximum nominal amount of €10 million, without interest, and without share warrants, over a period of no more than 30 months. ESGO supports Pixium Vision’s long-term development and has committed to take part in a capital increase in the event such a transaction is carried out. “We welcome this financing agreement and the trust ESGO has placed in us. Thanks to this flexible financial instrument, which significantly strengthens our financial outlook, we will actively pursue the development of our Prima system. We recently reached an important milestone now that the first patients implanted are equipped with second-generation glasses. These glasses combine residual natural vision and bionic vision. This is the first time such clinical success has been demonstrated and can be correlated with a potential improvement in quality of life. -

Final Report Amending ITS on Main Indices and Recognised Exchanges
Final Report Amendment to Commission Implementing Regulation (EU) 2016/1646 11 December 2019 | ESMA70-156-1535 Table of Contents 1 Executive Summary ....................................................................................................... 4 2 Introduction .................................................................................................................... 5 3 Main indices ................................................................................................................... 6 3.1 General approach ................................................................................................... 6 3.2 Analysis ................................................................................................................... 7 3.3 Conclusions............................................................................................................. 8 4 Recognised exchanges .................................................................................................. 9 4.1 General approach ................................................................................................... 9 4.2 Conclusions............................................................................................................. 9 4.2.1 Treatment of third-country exchanges .............................................................. 9 4.2.2 Impact of Brexit ...............................................................................................10 5 Annexes ........................................................................................................................12 -

Profil Financier Du CAC 40
Profil financier du CAC 40 Un CAC 40 agile et confiant en l’avenir 15e édition – Année 2020 15 ans, c’est l’âge de notre Profil financier du CAC 40. 15 ans d’une vie mouvementée pour un indice qui aura connu une belle croissance de son chiffre d’affaires et de ses résultats cumulés ainsi qu’un développement réel de ses fondamentaux, mais Nicolas Klapisz Associé, Responsable du également les affres de la crise financière de 2008 département Valuation, Modeling & Economics et, à présent, les conséquences d’une crise sanitaire sans précédent. Pour son quinzième anniversaire, nous Mais les conclusions de notre étude aurions souhaité offrir au Profil – et résident pour nous ailleurs : certes, surtout à ses lecteurs – une véritable les entreprises du CAC 40 ont connu envolée de la croissance et des records une contraction de leur activité et une en abondance. Las ! Les récents réduction de leurs marges inédites, le événements en ont décidé autrement et nier serait un non-sens. Cependant, sont venus contrarier nos ambitions. elles ont fait preuve, dans ce contexte, d’une agilité hors norme. Agilité Les chiffres sont têtus et l’on ne stratégique pour adapter leurs modèles pourra nier l’impact du Covid-19 : une économiques et développer leurs activité en chute de -15 %, un résultat activités digitales, agilité commerciale d’exploitation courant* en recul de -30 %, pour réduire l’impact de la pandémie sur un résultat net en baisse de près de le chiffre d’affaires au second semestre -60 % par rapport à l’an passé. L’ampleur 2020, agilité opérationnelle pour de ces évolutions est à l’image du maîtriser leurs coûts et agilité financière caractère inédit de cette pandémie pour piloter au mieux les résultats, les et des fermetures administratives dividendes et l’endettement.