DOCSLIB.ORG

Static Model of a Snowboard Undergoing a Carved Turn: Validation by Full‑Scale Test

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Static Model of a Snowboard Undergoing a Carved Turn: Validation by Full‑Scale Test Sports Engineering (2019) 22:15 https://doi.org/10.1007/s12283-019-0307-4 ORIGINAL ARTICLE Static model of a snowboard undergoing a carved turn: validation by full‑scale test Benoit Caillaud1 · Robert Winkler1 · Michael Oberguggenberger2 · Marc Luger3 · Johannes Gerstmayr1 Published online: 5 July 2019 © The Author(s) 2019 Abstract The purpose of this study was to defne a method for the validation of a numerical model representing a snowboard structure undergoing the conditions of a carved turn. A static load bench was developed to expose a snowboard to in-situ conditions. The deformed shape of the structure was measured with the use of retro-refective markers, whose positions in space were tracked by six cameras and determined by triangulation. The experimental set-up was idealized in a fnite element model, representing the composite structure and the loading environment. The model was validated by comparing the measured and computed displacement felds. The congruence between the two deformed surfaces was expressed by statistical means and constitutes the target function for optimization frameworks. Additionally, the contact pressure at the ground interface was experimentally assessed with the use of pressure measurement tape and compared with the numerical predictions. Keywords Snowboarding · Carving turn · FEM · Test validation · Contact pressure · Composite structure 1 Introduction Structural analysis applied to thin-walled structures has been widely used in the past, especially in the aerospace indus- * Benoit Caillaud try. Nonlinear investigation methods applied to composite [email protected] materials have been widely documented [1], and automa- http://www.uibk.ac.at/mechatronik/mekt/ tion techniques have made them afordable yet applicable Robert Winkler to other industrial sectors [2]. Regardless of the applica- [email protected] http://www.uibk.ac.at/mechatronik/mekt/ tion, the reliability of the numerical representations must be assessed through a stringent validation procedure, to control Michael Oberguggenberger [email protected] the quality of the engineering solutions. The development http://www.uibk.ac.at/techmath/ of sports equipment, and more particularly composite snow- Marc Luger board structures, is taken here as an illustration of how the [email protected] manufacturing environment can be numerically represented http://www.uibk.ac.at/mti/ by creating a ‘digital twin’ of the product. Johannes Gerstmayr Previous research on the behavior of snowboard struc- [email protected] tures have proposed models to represent the stifness at rest http://www.uibk.ac.at/mechatronik/mekt/ [3, 4]. In addition, analytical simulations of the dynamics of 1 Faculty of Engineering Sciences, Department a carved turn have been developed [5] and extensive knowl- of Mechatronics, University of Innsbruck, Technikerstraße edge is available to represent the on-snow conditions [6]. In 13, 6020 Innsbruck, Austria these aforementioned studies, the validation of the numerical 2 Faculty of Engineering Sciences, Unit of Engineering models consisted of comparing scalar values of the maxi- Mathematics, University of Innsbruck, Technikerstraße 13, mum displacements under bending and torsional loading 6020 Innsbruck, Austria independently. However, this approach is insufcient since it 3 Faculty of Engineering Sciences, Unit of Material does not guarantee the validity of the entire defected shape. Technology, University of Innsbruck, Technikerstraße 13, Furthermore, it does not account for combined problems 6020 Innsbruck, Austria Vol.:(0123456789) 15 Page 2 of 11 B. Caillaud et al. including contact formulations, as required in the present 2.2 Specimen investigated investigation. The conditions of a carved turn have been pre- viously investigated to qualify the interface loads [7] and the The prototype consisted of a simplifed snowboard structure behavior of a snowboard set on a carving angle [8]. Based manufactured according to the current industrial standards on this work, the present paper proposes a methodology to [9]. The structure featured a 5.55 mm constant thickness validate a mathematical model by comparing the global dis- wood core made out of ash ( 60 mm-wide strip along the placement felds. length of the snowboard, centered in the width) and poplar (remaining area), sandwiched between two composite skins made out of epoxy reinforced fberglass (each 0.665 mm 2 Experimental set‑up thick). The stacking sequence and corresponding fber ori- entations are shown in Sect. 3.2. The snowboard geometry To simulate the loading conditions occurring on a snow- was defned as symmetric twin-tip (two planes of symme- board during a carved turn, a static load bench was devel- try: xz-plane and yz-plane) and the sidecut had a constant oped and measurements of deformations were performed on radius of 7.05 m . The prototype’s geometrical parameters a simplifed snowboard structure. The experimental set-up are reported in Table 1 and illustrated in Fig. 1. is described within this section. 2.3 Static load bench 2.1 Local coordinate system and conventions The test bench developed in-house is represented in Fig. 2. The local coordinate system relative to the snowboard (O xyz ) It consisted of two independent structural profles (d) con- is defned as Cartesian (Fig. 1), such that the origin is posi- nected to the snowboard binding inserts via six screws each. tioned half-way between the centers of the binding loca- Each profle was equipped with a support beam (i) that could tions ( BR and BF ), and coincident with the horizontal plane be loaded with weight rings (j). The position of the weight (H), averaged from the four contact point locations ( Pi with rings was adjusted along the support beams to bring the ◦ ◦ i = 1, … ,4 ) on the bottom surface side of the snowboard. system to the desired tilt angle, ranging from 40 to 60 . The The lines P1P2 and P3P4 are referred to as ‘contact limits’. angular position was measured via the reference profles (e). The z-axis is normal to the plane (H), with the positive direc- The contact took place between the edge of the snowboard tion pointing towards the top surface of the snowboard. The and a rigid, fat contact plate (g) made out of 1.5 mm thick global x-axis runs along the length of the snowboard, defned aluminum. as the projection of BRBF onto (H). The y-axis runs across Once the weights were in position, the angular position the width according to the right-hand rule. As a convention, of the system was set with a threaded rod (c) and adjustment the front tip of the snowboard (referred to as ‘nose’) points screws (a) until static equilibrium was achieved. Thus, the towards the positive x, whereas the rear tip (referred to as threaded rod was no longer transmitting neither axial nor ‘tail’) points towards the negative x. The present conventions bending load. and reference systems are used throughout this paper unless A schematic representation of the forces and moments mentioned otherwise. applied to the snowboard is shown in Fig. 3. The application point of the input force P is represented at the center of the (a) ‘tail’ z ‘nose’ Table 1 Geometrical parameters of the specimen P O x P 1,2 2,3 (H) Parameter Abbreviation Value LC Total length L 1580 mm (b) L 1100 mm Contact length C y P2 P4 WN 291 mm BR BF Nose width W 248 mm O x Waist width W W 291 mm P1 P3 Tail width T hC 0 mm WW Camber height WT R WN h 34 mm Nose tip height F L h 28 mm Tail tip height R Sidecut radius R 7.05 m Fig. 1 t 6.88 mm Local coordinate system relative to the snowboard and conven- Total thickness T tions. a Front view. b Top view Page 3 of 11 15 Static model of a snowboard undergoing a carved turn: validation by full-scale test (a) adjustment screws interface, equal to the y-component of the input force P and (b) wall mounting proportional to the sine of the tilt angle : P = R = P () y y sin (1) This loading condition including the extra force component (c) threadedrod (j) weight rings is correspondingly regarded for the numerical representation of the experiment and throughout this paper. The impacts on (d) structural (i) support the validation procedure are discussed in Sect. 6. profiles beam 2.4 Measurement strategy (e)reference profile A motion tracking system (Vicon [10] and Vero v2.2 cam- eras) was used to capture the deformed shape of the struc- (f) snowboard ture. The measurement process consisted of positioning y spherical retro-refective markers on the top surface of the O x snowboard (such that they did not contribute to a stifen- ing of the structure) and measuring their position in space (h) connecting interfaces by triangulation, with the use of six cameras (see Fig. 4). (g) contactplate The absolute positioning error of the measurement system is reported to be 0.15 mm for static measurements [11]. Fig. 2 CAD model of the static load bench Due to the relatively small curvature of the deformed structure, the direct measurements of the marker positions were assumed to represent the deformation of the mid- −5 −1 z surface of the laminate ( max ≈ 5 × 10 mm leading to P ∼ 0.06 % positioning error). The angular positions of the y front and rear bindings with respect to the horizontal plane R were measured during the experiment via the reference pro- fles (see Fig. 2), on which extremities two Vicon markers were positioned. M Rz 2.5 Evaluation scheme θ Ry The reference stance (distance between both bindings) was set to s = 600 mm for the present measurements. Sym- Fig. 3 Schematic 2-D representation of the external forces and metrical loading conditions were defned: the total loading moments applied to the snowboard (side view).
Load more

Recommended publications
  • Dynamics of Carving Runs in Alpine Skiing. II.Centrifugal Pendulum with a Retractable Leg
    Dynamics of carving runs in alpine skiing. II.Centrifugal pendulum with a retractable leg. Serguei S. Komissarov Department of Applied Mathematics The University of Leeds Leeds, LS2 9JT, UK Abstract In this paper we present an advanced model of centrifugal pendulum where its length is allowed to vary during swinging. This modification accounts for flexion and extension of skier’s legs when turning. We focus entirely on the case where the pendulum leg shortens near the vertical position, which corresponds to the most popular technique for the transition between carving turns in ski racing, and study the effect of this action on the kinematics and dynamics of these turns. In partic- ular, we find that leg flexion on approach to the summit point is a very efficient way of preserving the contact between skis and snow. The up and down motion of the skier centre of mass can also have significant effect of the peak ground reaction force experienced by skiers, partic- ularly at high inclination angles. Minimisation of this motion allows a noticeable reduction of this force and hence of the risk of injury. We make a detailed comparison between the model and the results of a field study of slalom turns and find a very good agreement. This suggests that the pendulum model is a useful mathematical tool for analysing the dynamics of skiing. Keywords: alpine skiing, modelling, balance/stability, performance Introduction The skiing of expert skiers is characterised by smooth and rhythmic moves which are very reminiscent of a pendulum or metronome. This analogy invites mathematical modelling of skiing based on the pendulum action, which can be traced back to the pioneering work by Morawski (1973).
    [Show full text]
  • Section B (A Technical Understanding of Snowboarding)
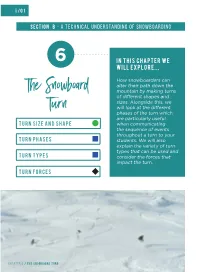
    B/01 Section b - A Technical Understanding of Snowboarding 6 In this chapter we will explore... How snowboarders can alter their path down the The Snowboard mountain by making turns of different shapes and sizes. Alongside this, we will look at the different Turn phases of the turn which are particularly useful Turn Size and Shape when communicating the sequence of events throughout a turn to your Turn phases students. We will also explain the variety of turn types that can be used and Turn types consider the forces that impact the turn. Turn forces CHAPTER 6 / THE SNOWBOARD TURN B/02 Turn Size and Shape Put simply, the longer the board spends in the fall line or the more gradually a rider applies movements, the larger the turn becomes. When we define the size of the turn we consider the length and radius of the arc: small, medium or large. The size of your turn will vary depending on terrain, snow conditions and the type of turn you choose to make. SMALL MEDIUM LARGE A rider’s rate of descent down the mountain is controlled mainly by the shape of their turns relative to the fall line. The shape of these turns can be described as open (unfinished) and closed (finished). A closed turn is where the rider completes the turn across the hill, steering the snowboard perpendicular to the fall line. This type of turn will easily allow the rider to control both their forward momentum and rate of descent. Closed turns are used on steeper pitches, or firmer snow conditions, to keep forward momentum down.
    [Show full text]
  • Instructor Guide
    INSTRUCTOR GUIDE Using the CASI Rider Improvement Program (RIP) The CASI Rider Improvement Program (RIP) has been developed with the goal of being a flexible, adaptable program that is suitable for group lessons, private lessons, or multi-week programs. Feel free to adapt the program to your specific needs regarding duration, number of sessions, etc. Each progress card in the program provides some standard Program Stages: information: Students will progress their skills through the following stages, Info: from 1 through 5. Following the completion of stage 5, they may Student name, date, resort info, instructor name and final com- choose either the Freestylin’ or Freeridin’ stage (or they may ments: choose to complete both!). • This area is useful in creating return lessons, as it ensures that your students have a record of your lesson with them. • Comments should be overall positive with suggestions for I. LITTLE RIPPERS A future practice and skills. II. LITTLE RIPPERS B Terrain: The areas of the mountain that students can expect to use in this III. LITTLE RIPPERS C stage. 1. BASICS Goals: • These are the technical outcomes that you will work 2. TURNING towards during your time in the particular stage of the program. 3. CRUISING • Note: Depending on your program format, each stage may range from 1 – 3 lessons. For some students it may be 4. SHREDDING realistic to accomplish all of the goals in one lesson, but this will not be the norm. 5. RIPPING Skills – Technical: 6a. FREESTYLIN’ - and/or - 6b. FREERIDIN’ • These represent the technical points of the lesson that the instructor will be introducing and practicing with the student.
    [Show full text]
  • The 4 Edges of the Snowboard
    2016 ISSUE 1 The Official Publication of the PSIA-AASI Central Division FLEXING ;) SNOWBOARD UPDATE | WHAT’S NEW IN EDUCATION | SNOWSPORTS DIRECTORS UPDATE | THE 4 EDGES OF A SNOWBOARD The “4 Edges” of a Snowboard By Chuck Roberts n the 1980’s, when snowboarding at most ski resorts was in its infancy, snowboards resembled stiff planks with little flexibility. Figure 1 is a photo of a 1987 Burton V-Tail, a stiff board with a running surface that resembled a V-bottom fishing boat. It also Ihad a location for a skeg (similar to a surf board) to aid when riding in powder. It appeared to work well in powder but had its limitations on groomed slopes. Turning the board involved unweighting and upper body rotation, resulting in skidded turns on groomed slopes. There was virtually no way to torsionally flex the board (torsional flex refers to the design features of a snowboard which allows it to twist along the longitudinal axis of the board), Figure 2). Fig. 1 Fig. 2 Fig. 3 Fig. 4 1987 Burton V-Tail “Cruiser” Torsional flex 1991 K2 TX “Gyrator” Modern twin tip snowboard Snowboards evolved into more flexible structures in the Likewise, the leading toe edge of the snowboard is engaged in early 1990’s as shown by the Gyrator in Figure 3. There was Figure 5C and the trailing toe edge is engaged in Figure 5D. some torsional flexibility but the narrow stance (rider’s feet close together) made it difficult to torsionally flex the board. The torsional flexing of the board when turning is performed Despite this, snowboarders discovered that torsionally flexing with the lower body and virtually no upper body influence, the board aided in turning.
    [Show full text]
  • Revival of the Steered Turn2
    Revival of the Steered Turn Take your skiing to a new dimension with this forgotten method of turning I've been wanting to write this article for the website for some time now, but have been overwhelmed with producing the DVDs. Well, I finally have a moment and it really needs to be done, so here goes. A terrible injustice has been perpetrated on one of our friends. The reputation of a very valuable turning technique has been viciously denigrated, and it's time we set things right. This article is meant to launch a campaign to do just that. Back in the mid 1990's a new type of ski burst on the scene, and the face of skiing changed forever. It was then that the parabolic ski, now known as the shape ski, made its debut. I remember when it happened. Bode Miller had just won the Junior Nationals on a pair of off-the-rack recreational skis that had a strange new shape. Parents of my racers were coming up to me in droves to ask if these new skis were for real. "Should we buy them for junior?" My answer was a resounding, 'yes, they are for real, and they're going to change the sport. Everyone is going to be skiing on these things, courses are going to be set differently, and teaching models are going to change. You need to buy these skis for junior or he'll be left in the dust!' We'll jump forward a dozen years. My predictions came true.
    [Show full text]
  • Special O Lym Pics C Oaching Q Uick Start G Uide
    Special Olympics Coaching Quick Start Guide ALPINE SKIING January 2008 Special Olympics Alpine Skiing Coaches Quick Start Guide Table of Contents Acknowledgements 3 Essential Components of Planning an Alpine Skiing Training Session 4 Principles of Effective Training Sessions 4 Tips for Conducting Safe Training Sessions 5 Alpine Skiing Attire 6 Under Layers 6 Outer Layers 7 Gloves or Mittens 8 Helmets 8 Hats 9 Goggles 9 Accessories 9 Alpine Skiing Equipment 10 Ski Boots 10 Skis 11 Bindings 11 Poles 12 Teaching Alpine Skiing Rules 13 Protest Procedures 13 Alpine Skiing Protocol & Etiquette 14 During Training 14 During Competition 15 Alpine Skiing Glossary 16 Appendix: Skill Development Tips 20 Beginner Skier 20 Skill Progression – Beginner Skier 20 Put on Equipment 21 Walk in Ski Boots 21 Walk on skis on snow 22 Side step 23 Straight run/ Straight wedge 24 Wedge turn to a stop or Flat ski turn to a stop 25 Riding a ski lift (ski lift awareness) 26 Controlled linked turns on easiest terrain 27 Novice Skier 28 Skill Progression – Novice Skier 28 Controlled linked turns on a novice course 29 Develop fundamental movement patterns through the turn 30 Alpine Skiing Quick Start Guide- January 2008 1 Special Olympics Alpine Skiing Coaches Quick Start Guide Ski the easiest terrain on the mountain under control 31 Vary turn size and shape 32 Perform a Christie-type turn (skidded turn) 33 Perform Christie-type linked turns (skidded turns) on an intermediate course 34 Intermediate Skier 35 Skill Progression – Intermediate Skier 35 Perform Christie-type
    [Show full text]
  • Finite Element Simulation of a Carving Alpine
    DISS. ETH NO. 16065 FINITE ELEMENT SIMULATION OF A CARVING SNOW SKI A dissertation submitted to the SWISS FEDERAL INSTITUTE OF TECHNOLOGY ZURICH for the degree of Doctor of Technical Sciences presented by PETER ANDREAS FEDEROLF diploma physicist, ETHZ born 18.01.1974 citizen of Federal Republic of GERMANY accepted on the recommendation of Prof. Jürg Dual, examiner Dr. Walter Ammann, co-examiner Dr. Anton Lüthi, co-examiner 2005 Abstract Winter sports have developed tremendously during the last century. This increased popularity has not only generated significant industrial activities, but has also boosted tourism in many mountainous regions. The design of new skiing equipment has to date always been the work of expert craftsmen, who improved the existing equipment in expensive and time-consuming prototyping and testing cycles. Nowadays, advanced numerical simulation tools offer new ways to assist ski manufacturers in the development of new equipment designs and shorten the required prototyping and testing cycles. Furthermore, numerical simulation methods offer new ways to analyse the interaction between skier, skiing equipment, and snow, and they offer the oportunity to analyse the impact of single parameters on the turn characteristics. The primary objective of this thesis is to develop a finite element simulation of the ski- binding system in the situation of a carved turn, specifically taking into account the ski-snow interaction. A quasi-static equilibrium of the external forces and moments is assumed, which allows to determine the boundary conditions on the model. These boundary conditions depend on the one hand on the forces and moments exerted by the skier onto the binding, on the other hand on the snow resistance pressure to the penetrating and sliding ski.
    [Show full text]
  • Giant Slalom by Georg Capaul
    Giant Slalom By Georg Capaul When ski technology evolves, skiing technique must follow suit. For that reason all skiers (not only racers) must be willing to alter their own skiing tactics to maximize the performance characteristics of the new gear. Racers get their cues from their coaches, but ski school client look to their instructors to inform them about the latest trends in equipment and how to get the best use from the new ski technology. If you'd like to use modern giant slalom technique as a springboard for improved all-around skiing ability, you need to focus on technical changes, basic movement patterns, phases of the turn, balance stance and weight distribution. Keeping your skis parallel, edge pressure, timing, and rhythm also warrant attention. Basics Most ski instructors and coaches share a basic philosophy about skiing. A solid understanding of the fundamentals is imperative. The main objective, whether the skier is trying to amass World Cup points or a typical day of free skiing they try to use the center of the skis in order to take full advantage of ski characteristics. For some people this translates into carving a perfect turn under all conditions in any terrain and at any speed. Others may be content to simply get more efficient use out of their skis design. Before the advent of shaped skis the technical focus of giant slalom skiers was to create angulation through significant separation of the lower and upper body (hip angulation) and to ski with pronounced counter- rotation. Another emphasis was to up-unweight the skis to initiate the turn.
    [Show full text]
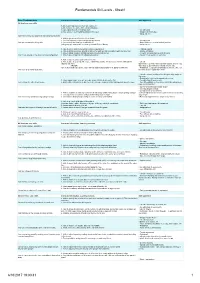
  • Instructors Information for Fundamentals Ski Levels
    Fundamentals Ski Levels - Sheet1 Core Fundamentals Instructor information, Learning outcome Skill aquisition Ski level one core skills 1.Able to pick up and carry their ski equipment 2.Able to name the parts of the ski and bindings 3.Can explain how their bindings work • Co-ordination 4.Have awareness of clothing and protective gear • Equipment knowledge • Independence I can safely carry my equipment and know how it works 1. Able to get snow off bottom of their boots 2. Can line up boots in the bindings and put skis on • Co-ordination I can put on and take off my skis 3. Can release the bindings to take skis off • Basic Balance – centred athletic position (using any age appropriate method eg. Hands/ Poles / Boots) • Independence 1. Able to say in basic terms what a balanced position is • Flatland mobility 2. Able to balance & move around on flat terrain with one ski on, pushing with the other foot • Stance & balance: 3. Able to stand & walk in a balanced position with both skis on - Fore/aft: Centred stance whilst moving I can move around on my skis in a balanced position 4. Able to do a straight run in a balanced position - Lateral: Even weight on each foot 1. Able to side step &/or duck walk on the flat 2. Able to side step up a gentle slope, maintaining parallel skis across the fall line without skis • Lateral – slipping sideways Duck walk: legs wider than hip width apart & skis on edge AND/OR Side Step: Legs inclined to hill and skis on edge Able to duck walk up a gentle slope without slipping backwards or stepping on own skis • Rotational – Legs turned outwards so skis are closer at I can side step and/or duck walk.
    [Show full text]
  • Asymmetries in the Technique and Ground Reaction Forces of Elite Alpine Skiers Influence Their Slalom Performance
    applied sciences Article Asymmetries in the Technique and Ground Reaction Forces of Elite Alpine Skiers Influence Their Slalom Performance Matej Supej 1,* , Jan Ogrin 1, Nejc Šarabon 2 and Hans-Christer Holmberg 3,4 1 Faculty of Sport, University of Ljubljana, 1000 Ljubljana, Slovenia; [email protected] 2 Faculty of Health Sciences, University of Primorska, Polje 42, 6310 Izola, Slovenia; [email protected] 3 Department of Physiology and Pharmacology, Biomedicum C5, Karolinska Institute, 171 77 Stockholm, Sweden; [email protected] 4 China Institute of Sport and Health Science, Beijing Sport University, Beijing 100084, China * Correspondence: [email protected]; +386-68-161-271 Received: 15 September 2020; Accepted: 15 October 2020; Published: 18 October 2020 Abstract: Background: Although many of the movements of skiers are asymmetric, little is presently known about how such asymmetry influences performance. Here, our aim was to examine whether asymmetries in technique and the ground reaction forces associated with left and right turns influence the asymmetries in the performance of elite slalom skiers. Methods: As nine elite skiers completed a 20-gate slalom course, their three-dimensional full-body kinematics and ground reaction forces (GRF) were monitored with a global navigation satellite and inertial motion capture systems, in combination with pressure insoles. For multivariable regression models, 26 predictor skiing techniques and GRF variables and 8 predicted skiing performance variables were assessed, all of them determining asymmetries in terms of symmetry and Jaccard indices. Results: Asymmetries in instantaneous and sectional performance were found to have the largest predictor coefficients associated with asymmetries in shank angle and hip flexion of the outside leg.
    [Show full text]
  • Eskimos Ski System Kids
    ESKIMOS SKI SYSTEM KIDS We have developed the unique ESKIMOS ski system to simplify the choice of courses for our guests. It is built like an igloo. The lessons Park, Penguin, Seal and Polar Bear are the igloo’s fundament. Beginners can learn in a quick and safe way how to ski controlled and intermediate beginners can optimise their skills.Those who want to fly high can look up to the roof of the igloo, to the four Allround lessons and the Your Choice! ski camp. Advanced skiers can bring the specific techniques to perfection in these lessons and reach for the stars. PARK Park Penguin Seal Polar Bear Walking and moving Snowplough turns First time change of direction Advanced parallel turn around on ski’s First runs on blue slopes in parallel on blue slopes First runs in the kids park Using the lift Introduction parallel turn First carved turns Speed control and stopping Crossing the slopes parallel on blue slopes Introduction parallel turn Introduction to turning Behaviour on the slopes (FIS Safe skiing on blue slopes on red slopes Introduction to the code) Introduction carving while Weight and unweight magic carpet crossing the slopes move ment Parallel stop Allround 1 Allround 2 Allround 3 Allround 4 Advanced parallel turn Introduction short turn Introduction carved turn Advanced mogul short turn on red slopes on red slopes on red slopes Advanced carved turn Introduction carved turn Advanced carved turn Advanced short turn on red slopes on blue slopes on blue slopes on red slopes Varying size of carved turns Introduction short turn Introdution parallel turn Introduction mogul short turn Safe skiing on varying terrain on blue slopes on black slopes Master easy moguls Performance in varying Introcution fakie skiing Advanced fakie skiing Advanced parallel turn terrain on blue slopes First slided 180°s on the slope on black slopes First jumped 180°s on the slopes Your Choice! Your Choice! is the ski camp You and your peers decide for all young skiers up to together with your coach 18 years who know what the content of this ski camp.
    [Show full text]
  • Physics of Skiing: the Ideal–Carving Equation and Its Applications
    Physics of Skiing: The Ideal–Carving Equation and Its Applications U. D. Jentschura and F. Fahrbach Universit¨at Freiburg, Physikalisches Institut, Hermann–Herder–Straße 3, 79104 Freiburg im Breisgau, Germany February 2, 2008 Abstract Ideal carving occurs when a snowboarder or skier, equipped with a snowboard or carving skis, describes a perfect carved turn in which the edges of the ski alone, not the ski surface, describe the trajectory followed by the skier, without any slipping or skidding. In this article, we derive the “ideal-carving” equation which describes the physics of a carved turn under ideal conditions. The laws of Newtonian classical mechanics are applied. The parameters of the ideal-carving equation are the inclination of the ski slope, the acceleration of gravity, and the sidecut radius of the ski. The variables of the ideal-carving equation are the velocity of the skier, the angle between the trajectory of the skier and the horizontal, and the instantaneous curvature radius of the skier’s trajectory. Relations between the slope inclination and the velocity range suited for nearly ideal carving are discussed, as well as implications for the design of carving skis and snowboards. Keywords: Physics of sports, Newtonian mechanics PACS numbers: 01.80.+b, 45.20.Dd 1 Introduction The physics of skiing has recently been described in a rather comprehensive book [1] which also contains further references of interest. The current article is devoted to a discussion of the forces acting on a skier or snowboarder, and to the derivation of an equation which describes “ideal carving”, including applications of this concept in practice and possible speculative implications for the design of technically advanced skis and snowboards.
    [Show full text]