The Shuffle Conjecture
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Last Name First Name Middle Name Reference No. Collection Site
PASSPORTS APPLIED IN PCG DUBAI/FSPsRCOsManila/VFS(PaRC) PASSPORTS READY FOR RELEASE AS OF 29 August 2021 RELEASING SECTION 8-12NN, 1-5PM, SUN-THU, EXCEPT HOLIDAYS TO SEARCH FOR YOUR NAME press "CONTROL F" OR "F3". If your name is already listed, please proceed to your designated Collection Site with your OLD PASSPORT AND OFFICIAL RECEIPT to claim your new e- passport. If the applicant cannot come personally to collect the passport, authorize someone to pick-up the passport. The following are the requirements: AUTHORIZATION LETTER, OLD PASSPORT, ORIGINAL RECEIPT, AND ORIGINAL AND COPY OF VALID IDENTIFICATION CARD OF AUTHORIZED REPRESENTATIVE. WRITE THE REFERENCE NUMBER AT THE TOP OF YOUR RECEIPT UPON CLAIMING YOUR PASSPORT Middle Collection Last name First name Reference No. name Site AARTS ESRA MAE R. 2000106100360 DubaiPCG ABABA ROLANDO JR. I. 2000134000360 DubaiPCG ABACAN RENELYN D. 2000122300360 DubaiPCG ABAD MARIA EMMA D. 2000120550360 DubaiPCG ABAD CRISALDO B. 2000121900360 DubaiPCG ABAD ARIANNE FAYE D. 2000016765000 PaRC ABAD MICHELLE JANE D. 2000135890360 DubaiPCG ABAD MA. LAVINIA R. 2000037215000 PaRC ABAD SARAH T. 2000037435000 PaRC ABAD GERALD E. 2000137190360 Dubai PCG ABAD PAOLO NOEL R. 2000038495000 PaRC ABADILLA JOJO A. 2000017505000 PaRC ABAGAT LILIA D. 2000037825000 PaRC ABALAYAN AUDREIL O. 2000017855000 PaRC ABALAYAN MILDRED O. 2000017865000 PaRC ABALLE JESIE FE S. 2000136280360 Dubai PCG ABALOS ARRA BELLA J. 2000019735000 PaRC ABALOS BLENS RADIEL S. 2000136930360 Dubai PCG ABALOS LIZA C. 2000037855000 PaRC ABALOS ALDRIN D. 2000038055000 PaRC ABALUS XYNE AUBRIELLE C. 2000124910360 DubaiPCG ABANICO DANILO JR. M. 2000106680360 DubaiPCG ABAO DANIEL V. 2000120610360 DubaiPCG ABAO MARY LYN A. -

The Old Maid and the Thief by Gian Carlo Menotti a Grotesque Opera in 14 Scenes
THE BELHAVEN UNIVERSITY DEPARTMENT OF MUSIC Dr. Stephen W. Sachs, Chair presents Two Hilarious American Operas: The Telephone by Gian Carlo Menotti An Opera Buffa in One Act The Old Maid and the Thief by Gian Carlo Menotti A Grotesque Opera in 14 Scenes Dr. Christopher Shelt, Artistic Director Friday, November 19, 2010 at 7:30pm & Saturday, November 20, 2010 at 2:30pm Belhaven University Center for the Arts Concert Hall BELHAVEN UNIVERSITY DEPARTMENT OF MUSIC MISSION STATEMENT The Music Department seeks to produce transformational leaders in the musical arts who will have profound influence in homes, churches, private studios, educational institutions, and on the concert stage. While developing the God-bestowed musical talents of music majors, minors, and elective students, we seek to provide an integrative understanding of the musical arts from a Christian world and life view in order to equip students to influence the world of ideas. The music major degree program is designed to prepare students for graduate study while equipping them for vocational roles in performance, church music, and education. The Belhaven University Music Department exists to multiply Christian leaders who demonstrate unquestionable excellence in the musical arts and apply timeless truths in every aspect of their artistic discipline. The Music Department would like to thank our many community partners for their support of Christian Arts Education at Belhaven University through their advertising in “Arts Ablaze 2010-2011” (should be published and available on or before September 30, 2010). Special thanks tonight to Bo-Kays Florist for our reception table flowers. It is through these and other wonderful relationships in the greater Jackson community that makes an afternoon like this possible at Belhaven. -

Curriculum Vitae
CURRICULUM VITAE Gian Carlo Di Renzo, MD, PhD Professional Address Gian Carlo Di Renzo Professor and Chairman Dept. of Ob/Gyn Director, Centre for Perinatal and Reproductive Medicine Santa Maria della Misericordia University Hospital 06132 San Sisto - Perugia - Italy tel. +39 075 5783829 tel. +39 075 5783231 fax +39 075 5783829 [email protected] Date of birth: 13 June 1951 Place of birth: Verona, Italy Citizenship: Italian 1 Director of Education and Communication & Past General Secretary of FIGO University of Perugia, Perugia, Italy. Prof. Gian Carlo Di Renzo is currently Professor and Chair at the University of Perugia (2004 - ), and Director of the Reproductive and Perinatal Medicine Center (1996 - ) , former Director of the Midwifery School (2004-2016), University of Perugia, in addition to being the Director of the Permanent International and European School of Perinatal and Reproductive Medicine (PREIS) in Florence (2012 - ) . After graduation cum laude at Medical School of the University of Padova (1975) , he was a research fellow at the Universities of Verona, Messina and Modena. After training at CHUV in Lausanne (Switzerland), at UCH in London (UK), at the University of Texas in Dallas (USA), and at the Catholic University in Nijmegen (NL) (1977-1982), he became a senior researcher at the University of Perugia. Since 2004 he is Professor and Chairman of the Department of Obstetrics and Gynecology at the University or Perugia., Chairman of the Midwifery School in the year 2004 to 2016, of the Ob Gyn Resident’s program since 2008 and of the PhD Program in Translational Medicine since 2012. He was general Secretary of the Italian Society of Perinatal Medicine, President of the Italian Society of Ultrasound in Obstetrics and Gynecology, Secretary-Treasurer of the European Association of Perinatal Medicine, President from 2000 to 2002, 2002-2008 Executive Director and Chairman of the Educational Committee, Vice President of the World Association of Perinatal Medicine ( 2007-2013) . -

Musical Influences Statistics
Composers Individuals’ Influence on Composer Composer’s Influence on Others Overall Name Sum+ Sum- n Mean1 Mean2 S. D. Sum- Sum+ n/n+ Sum Mean S. D. Rank Adam, Adolphe 0 0 4 1.90 0. .87 0 0 2/3 6.4 2.25 .35 277 Adams, John 0 9 13 3.07 -.69 1.54 - - - - - - 191 Adler, Samuel 0 0 6 2.58 0. .88 - - - - - - 312 Alain, Jehan 0 0 7 2.49 0. .98 - - - - - - 308 Albéniz, Isaac 3 6 11 3.39 -.27 1.30 0 0 8 19.9 2.49 .83 87 Albinoni, Tomaso 1 0 3 2.40 .33 .83 0 0 6 19.3 3.22 2.05 135 Alfvén, Hugo 0 2 8 3.36 -.25 1.35 - - - - - - 384 Alkan, (Charles-)Valentin 0 6 12 3.68 -.50 1.49 0 0 1 4.0 4.0 0. 317 Allegri, Gregorio 0 0 1 2.30 0. 0. 0 5 2 5.5 2.75 1.35 459 Alwyn, William 0 2 16 3.21 -.13 .79 - - - - - - 491 Amram, David 0 0 0 - - - - - - - - - 478 Anderson, Leroy 0 0 3 2.63 0. .66 - - - - - - 432 Andriessen, Louis 0 7 12 2.75 -.58 1.42 - - - - - - 360 Arensky, Anton 0 3 7 3.54 -.43 1.01 0 0 3 7.5 2.50 .73 323 Argento, Dominick 0 7 9 3.23 -.78 1.48 0 0 1 1.5 1.50 0. 296 Arne, Thomas 1 0 4 2.63 .25 1.20 - - - - - - 252 Arnold, Malcolm 0 2 10 2.83 -.20 .78 - - - - - - 155 Auber, Daniel-François-Esprit 2 0 5 3.12 .40 1.75 0 0 15 37.4 2.49 1.15 447 Auric, Georges 0 1 6 2.75 -.17 .71 0 0 1 1.4 1.40 0. -

FIRST NAME MI LAST NAME FELLOW DATE SECTION Theodore A
FIRST NAME MI LAST NAME FELLOW DATE SECTION Theodore A. Aanstoos 04/01/2001 Cent Texas Said I. Abdel-Khalik 06/01/1999 Atlanta Rohan C. Abeyaratne 03/01/1998 Boston H. Norman Abramson 01/01/1971 San Antonio Memis Acar 06/01/2007 United Kingd Salvador M. Aceves-Saborio 07/01/2001 Sumanta Acharya 08/05/2008 Baton Rouge Jan D. Achenbach 01/01/1979 Chicago Allan J. Acosta 01/01/1979 Orange Cnty Paul J. Adam 10/01/1997 Arizona John J. Adamczyk 02/01/2001 Cleveland Frank C. Adamek 05/01/1997 Nw Houston Douglas E. Adams 03/18/2011 Cent Indiana George G. Adams 05/01/1995 Boston John C. Adams 07/01/1995 Highland Rim William J. Adams 11/01/2000 Santa Clara Alva L. Addy 01/01/1984 Nebraska Kenneth L. Adler 01/01/1986 San Fernando Suresh G. Advani 06/01/1999 Delaware Abdollah Afjeh 04/02/2012 Nw Ohio Naval K. Agarwal 05/01/1996 Western Wash Ramesh K. Agarwal 02/01/1994 St Louis Avinash K. Agarwal 9/1/2013 India Mahesh Aggarwal 10/01/1995 Erie Suresh K. Aggarwal 06/01/2005 Chicago Alice M. Agogino 10/01/2005 San Francisc Ajay K. Agrawal 09/01/2004 Birmingham Giridhari L. Agrawal 04/01/2004 Hartford Sunil K. Agrawal 01/01/2004 Delaware John W. Ahlen 05/01/2003 Arkansas Arthur G. Ahlstone 12/01/1988 Channel Isl Goodarz Ahmadi 03/01/1997 Syracuse Mehdi Ahmadian 05/01/1998 Virginia A. K. W. Ahmed 10/02/2012 Quebec Xiaolan Ai 04/02/2012 Canton-All-M Adnan Akay 09/01/1989 Pittsburgh Hadi K. -

San Diego County Treasurer-Tax Collector 2019-2020 Returned Property Tax Bills
SAN DIEGO COUNTY TREASURER-TAX COLLECTOR 2019-2020 RETURNED PROPERTY TAX BILLS TO SEARCH, PRESS "CTRL + F" CLICK HERE TO CHANGE MAILING ADDRESS PARCEL/BILL OWNER NAME 8579002100 11-11 GIFT TRUST 04-01-96 8579002104 11-11 GIFT TRUST 04-01-96 8579002112 11-11 GIFT TRUST 04-01-96 8679002101 11-11 GIFT TRUST 04-01-96 8679002105 11-11 GIFT TRUST 04-01-96 8679002113 11-11 GIFT TRUST 04-01-96 8779002102 11-11 GIFT TRUST 04-01-96 8779002106 11-11 GIFT TRUST 04-01-96 8779002114 11-11 GIFT TRUST 04-01-96 8879002103 11-11 GIFT TRUST 04-01-96 8879002107 11-11 GIFT TRUST 04-01-96 8879002115 11-11 GIFT TRUST 04-01-96 5331250200 1141 LAGUNA AVE L L C 2224832400 1201 VIA RAFAEL LTD 3172710300 12150 FLINT PLACE LLC 2350405100 1282 PACIFIC OAKS LLC 4891237400 1360 E MADISON AVENUE L L C 1780235100 138 SUN VILLA CT LLC 8894504458 138 SUN VILLA CT LLC 2222400700 1488 SAN PABLO L L C 1300500500 15195 HWY 76 TRUST 04-084 1473500900 152 S MYERS LLC 4230941300 1550 GARNET LLC 2754610900 15632 POMERADO ROAD L L C 1678 COUNTRY CLUB DR ESCONDIDO CA 92029 TRUST 05-07- 2325114700 18 1678 COUNTRY CLUB DR ESCONDIDO CA 92029 TRUST 05-07- 8894616148 18 2542212300 1697A LA COSTA MEADOWS L L C 2542212400 1697A LA COSTA MEADOWS L L C 6461901900 1704 CACTUS ROAD LLC 5333021200 1750 FIFTH AVENUE L L C 2542304001 180 PHOEBE STREET LLC 5392130600 1815-19 GRANADA AVENUE LLC 5392130700 1815-19 GRANADA AVENUE LLC 2643515400 18503 CALLE LA SERRA L L C 2263601300 1991 TRUST 12-02-91 AND W J K FAMILY LTD PARTNERSHIP 5650321400 1998 ENG FAMILY L L C 5683522300 1998 ENG FAMILY L L -

Gian Carlo Menotti's the Unicorn, the Gorgon, and the Manticore
University of Richmond UR Scholarship Repository Music Department Concert Programs Music 4-6-2012 Gian Carlo Menotti's The nicorU n, the Gorgon, and the Manticore Department of Music, University of Richmond Follow this and additional works at: http://scholarship.richmond.edu/all-music-programs Part of the Dance Commons, and the Music Performance Commons Recommended Citation Department of Music, University of Richmond, "Gian Carlo Menotti's The nicU orn, the Gorgon, and the Manticore" (2012). Music Department Concert Programs. 36. http://scholarship.richmond.edu/all-music-programs/36 This Program is brought to you for free and open access by the Music at UR Scholarship Repository. It has been accepted for inclusion in Music Department Concert Programs by an authorized administrator of UR Scholarship Repository. For more information, please contact [email protected]. THE UNIVERSITY OF RICHMOND DEPARTMENT OF MUSIC UNIVERSITY OF RICHMOND LIBRARIES llllllllllllllllllllllllllllllllllllllllllllllllllllllllllllllll 3 3082 01 080 8292 SCHOLA CANTORUM UNIVERSITY DANCERS ENSEMBLE An Hoc Gian Carlo Menotti's 7he Unicorn, 7he (Jof'_Jon ani7!Je Manficore Joseph Flutn1nerfelt, guest conductor Jeffrey Riehl, artistic director Anne van Gelder and Darby Harris, choreography anlin concert WOMEN'S CHORALE David Pedersen, conductor Mary Beth Bennett, accompanist Friday, April6, 2012 7:30p.m. Camp Concert Hall Booker Hall of Music WOMEN'S CHORALE David Pedersen, conductor Mary Beth Bennett, accompanist Cantate Domino Guy Forbes Cantate Domino canticum novum, Sing to the Lord a new song, Cantate Domino omnis terra. Sing to the Lord all the earth. Cantate Domino et benedicite nomini ejus. Sing to the Lord and bless his name. -

Luigi Dallapiccola's Il Prigioniero and Gian Carlo
LUIGI DALLAPICCOLA'S IL PRIGIONIERO AND GIAN CARLO MENOTTI'S THE CONSUL: A COMPARATIVE STUDY by JENNIFER GRAHAM STEPHENSON PAUL H. HOUGHTALING, COMMITTEE CHAIR SUSAN CURTIS FLEMING NIKOS A. PAPPAS STEPHEN V. PELES JONATHAN WHITAKER ELIZABETH AVERSA A DOCUMENT Submitted in partial fulfillment of the requirements for the degree of Doctor of Musical Arts in the School of Music in the Graduate School of The University of Alabama TUSCALOOSA, ALABAMA 2016 Copyright Jennifer Graham Stephenson 2016 ALL RIGHTS RESERVED ABSTRACT As art reflects life, so too does it hold a mirror to the lives of the people who create it. The turbulent events of the first decades of the twentieth century, including two World Wars and the rise of Italian Fascism and German Nazism in the 1920s and 30s, affected millions of lives across several continents. This document explores the ways in which Luigi Dallapiccola (1904– 1973) and Gian Carlo Menotti (1911–2007) voice their reactions to these events in their operas, Il Prigioniero (1948) and The Consul (1950). Italian composer Luigi Dallapiccola spent twenty months in internment during the First World War, and would be forced on several occasions to go into hiding during the Second World War. His opposition to Mussolini and the Italian Fascists, coupled with his quasi–obsession with internment and freedom, led to his composition of three works of “protest music,” of which Il Prigioniero is the second. Il Prigioniero tells the story of a prisoner of the Inquisition, his attempt at escape and eventual capture. Italian-American composer Gian Carlo Menotti emigrated to the United States in 1928, at age seventeen, and spent a great much of his time traveling and working in various countries. -

Oss Personnel Files - Rg 226 Entry 224 12/23/2010
OSS PERSONNEL FILES - RG 226 ENTRY 224 12/23/2010 LAST NAME FIRST NAME M I RANK or SERIAL BOX NOTES LOCATION Aaberg Caf-3 E T-5 37541999 1 230/86/26/03 Aalbu Sigurd J S/Sgt 37091702 1 230/86/26/03 Aanonsen Olaf H Cpl 32440677 1 230/86/26/03 Abbenante Helen G Cpl A125357 1 230/86/26/03 Abbote Frank Pfc 32985690 1 230/86/26/03 Abbote John A T-3 42048684 1 230/86/26/03 Abbott Delbert H Pvt 35314960 1 230/86/26/03 Abbott Floyd H Pfc 39535381 1 230/86/26/03 Abbott Frederick K Caf-11 1 230/86/26/03 Abbott James E S/Sgt 12063651 1 230/86/26/03 Abbott James F T-5 11102233 1 230/86/26/03 Abbott Norman SP 2/c 5634486 1 230/86/26/03 Abbott Robert J Sgt 12140436 1 230/86/26/03 Abbott Victor J M/Sgt 32455694 1 230/86/26/03 Abee Robert V T-4 34437404 1 230/86/26/03 Abel Arthur A 1st Lt 1181596 1 230/86/26/03 Abel Calvin J T-5 16117938 1 230/86/26/03 Abel John C 1 230/86/26/03 Abele Charles R 1st Lt 462544 1 230/86/26/03 Abele Herbert, Jr. A 2nd Lt 1329784 1 230/86/26/03 Abendschein Norman W Sgt 33191772 1 230/86/26/03 Abernathy James D 1st Lt 343733 1 230/86/26/03 Abney James K 1 230/86/26/03 Abraham Michael K Capt 1010362 1 230/86/26/03 Abrahamovitz Moses T/Sgt 33751543 2 230/86/26/03 Abrahams Isaace L 39090318 1 230/86/26/03 Abrahamson Albert Pvt 32966288 1 230/86/26/03 Abrahamson John D P-4 1 230/86/26/03 Abrams Allen P-7 2 230/86/26/03 Abrams Leonard 2 230/86/26/03 Abrams Melville F T-4 32978088 2 230/86/26/03 Abrams Ruth B Caf-7 2 230/86/26/03 Abrignani Vincent A Maj 1297132 2 230/86/26/03 Abrogast Hazel E Caf-4 2 230/86/26/03 Abromaitis Alexander -
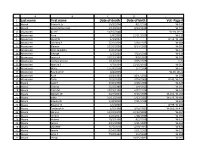
Last Name First Name Date of Death Date of Birth Vol.-Page
A B C D E 1 Last name First name Date of death Date of birth Vol.-Page # 2 Waack Edwin H Sr 10/3/2004 8/1/1916 W-136 3 Waack Helen M (Lantto) 1/14/2012 3/14/1919 W-712 4 Waananen Ailie E 10/16/2006 W-19, W-23 5 Waananen Arne 2/6/2005 12/11/1920 W-119 6 Waananen Daryl W 1/3/2007 W-14, W-704 7 Waananen Dorothy E 7/26/2009 5/30/1925 W-688 8 Waananen Eleanor 10/31/2006 8/14/1929 W-581 9 Waananen Ellen Jaakkola 1/20/2002 W-374 10 Waananen George 2/2/2001 7/24/1915 W-514 11 Waananen James A 10/21/1996 9/9/1952 W-245 12 Waananen Leona Caroline 1/14/2007 7/25/1925 Y-71 13 Waananen Martha S 4/7/1994 12/15/1916 W-262 14 Waananen Mary 12/24/2006 1/7/1914 W-575 15 Waananen Raymond P 9/4/2005 W-36, W-42 16 Waananen Ruth 1/19/1991 10/1/1921 W-299 17 Waananen Turie 1/25/2005 4/24/1909 W-43, W-123 18 Waara Aale R 3/30/1996 2/28/1908 W-325 19 Waara Charles 2/21/1980 2/4/1912 W-267 20 Waara Clara M 10/29/1996 4/12/1916 W-245 21 Waara Delbert W 3/24/2004 9/15/1939 W-151, W-160 22 Waara Edna 10/11/2006 1/13/1922 W-573, W-580 23 Waara Edward D 1/28/2010 7/21/1934 W-634 24 Waara Eleanor G 5/5/2005 W-99, W-102 25 Waara Frederick A 6/5/1990 3/10/1951 W-300, W-415 26 Waara Henry J 10/31/1978 12/13/1895 W-267 27 Waara Henry J 1/22/2011 5/28/1949 W-593 28 Waara Hubert 10/2/1999 8/2/1915 W-531 29 Waara James 4/15/2008 5/11/1937 W-652 30 Waara jeanette 1/27/2010 4/29/1927 W-644 31 Waara Jennie 5/14/1980 11/1/1911 W-275 32 Waara John C 7/22/1993 1/3/1912 W-268 33 Waara Lempi 10/25/1891 W-267 A B C D E 34 Waara Lillian 5/1/1980 9/1/1900 W-275 35 Waara Maria 7/10/2010 -

The Wild Side Catalina
FALL 2014 Catalina: The Wild Side ARTISTS CAPTURE ISLAND’S CONSERVATION PAGE 2 Message from the President e are by nature storytellers. We tell each plein air painters, who are capturing the Island’s other about our work, our families, our Conservancy-led restoration in their art, this issue Wdreams and our aspirations. tells some of their Catalina stories. We invite you to see how the artists tell their own stories through Most of us who know and love the Island have their paintings at Catalina: The Wild Side Art our own Catalina story. Like most, my Catalina Show & Sale on October 26 in Balboa. story starts with boarding a boat, where I begin to relax as my mind’s eye quickens. It is always the In this issue, we also describe how we are creating beginning of an adventure, the leaving behind of the future of the Conservancy with Imagine one world and the embracing of another. Catalina, a long-range strategic vision and master plan. Developed over several years of study and When I first came to the Island as a marine planning, Imagine Catalina serves as a blueprint ecology graduate student, Catalina provided life- for the future of the Conservancy. It aspires to changing experiences as I was both challenged use the good work, resources and success of the and rewarded in many ways: physically with a past 42 years to serve as a sustainable model for rigorous underwater field research program; conservation in a lived landscape. intellectually with my course work, research Conservancy Times is a and teaching responsibilities; and, perhaps most We’re also recounting our work over the past year biannual publication of the importantly, emotionally as I was lucky enough in a new and more engaging Annual Report. -

Genealogical Queries
Swedish American Genealogist Volume 14 Number 1 Article 5 3-1-1994 Genealogical Queries Follow this and additional works at: https://digitalcommons.augustana.edu/swensonsag Part of the Genealogy Commons, and the Scandinavian Studies Commons Recommended Citation (1994) "Genealogical Queries," Swedish American Genealogist: Vol. 14 : No. 1 , Article 5. Available at: https://digitalcommons.augustana.edu/swensonsag/vol14/iss1/5 This Article is brought to you for free and open access by the Swenson Swedish Immigration Research Center at Augustana Digital Commons. It has been accepted for inclusion in Swedish American Genealogist by an authorized editor of Augustana Digital Commons. For more information, please contact [email protected]. Genealogical Queries Genealogical queries from subscribers to Swedish American Genealogist will be listed here free of charge on a "space available" basis. The editor reserves the right to edit these queries to conform to a general format. The enquirer is responsible for the contents of the query. Svensson, Svensdotter I am trying to trace a group of six siblings who emigrated to America: 1. Anna Wilhelmina Svensdotter, b. in Gränna 12 Oct. 1857; emigr. from Gränna 8 May 1875. Probably deceased by the time the mother's estate inventory (bouppteckning) was held 1898. 2. Carl August Svensson, b. in Gränna 15 Sept. 1861; emigr. to New York 3 June 1881. 3. Emma Svensdotter, b. in Gränna 7 Dec. 1863; emigr. 5 May 1880. 4. Gustaf Svensson, b. in Gränna 8 June 1866; emigr. 22 Oct. 1889. 5. Alfred Svensson, b. in Gränna 31 Oct. 1870; emigr. from Adelöv Parish (Jön.) 29 Dec. 1890.