DOCSLIB.ORG

Ray Theory Transmission Theories of Optics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Ray Theory Transmission Theories of Optics Ray Theory Transmission Theories of Optics • Light is an electromagnetic phenomenon described by the same theoretical principles that govern all forms of electromagnetic radiation • Electromagnetic optics provides the most complete treatment of light phenomena in the context of classical optics. • quantum theory provides the successful explanation for light-matter interaction(emission & absorption) • Electromagnetic radiation propagates in the form of two mutually coupled vector waves, an electric field- wave & magnetic field wave(classical optics) • Many optical phenomena such as diffraction is described by a single scalar wave function(scalar wave optics or wave optics) • Ray optics is the limit of wave optics when the wavelength is very short. Quantum Optics Electromagnetic Optics Wave Optics Ray Optics Engineering Model • Depending on the structure, we may use ray optics or electromagnetic optics Electromagnetic Optics • Electromagnetic radiation propagates in the form of two mutually coupled vector waves, an electric field wave & a magnetic field wave. Both are vector functions of position & time. • In a source-free, linear, homogeneous, isotropic & non-dispersive media, such as free space, these electric & magnetic fields satisfy the following partial differential equations, known as Maxwell’ equations: E H [1] t H E [2] t E 0 [3] H 0 [4] • In Maxwell’s equations, E is the electric field expressed in [V/m], H is the magnetic field expressed in [A/m]. [F/m] : Electric permittivi ty [H/m] : Magnetic permeabili ty : is divergence operation : is curl operation • The solution of Maxwell’s equations in free space, through the wave equation, can be easily obtained for monochromatic electromagnetic wave. All electric & magnetic fields are harmonic functions of time of the same frequency. Electric & magnetic fields are perpendicular to each other & both perpendicular to the direction of propagation, k, known as transverse wave (TEM). E, H & k form a set of orthogonal vectors. Electromagnetic Plane wave in Free space Ex Direction of Propagation k x z z y By An electromagnetic wave is a travelling wave which has time varying electric and magnetic fields which are perpendicular to each other and the direction of propagation, . Linearly Polarized Electromagnetic Plane wave E e E cos(ωt - kz) [5] x 0x H e H cos(ωt kz) y 0 y [6] where : ω 2f : Angular frequency [rad/m] [7] k : Wavenumber or wave propagation constant [1/m] 2 :Wavelength [m] k E0x [] : intrinsic (wave) impedance [8] H 0 y 1 v [m/s] : velocity of wave propagation [9] E and B have constant phase in this xy plane; a wavefront z E E k Propagation B E x E = E sin(wt–kz) x o z , has the same A plane EM wave travelling alongz Ex (or By) at any point in a given xy plane. All electric field vectors in a givenxy plane are therefore in phase. The xy planes are of infinite extent in thex and y directions. Wavelength & free space • Wavelength is the distance over which the phase changes by 2 . v [10] f • In vacuum (free space): 9 10 7 0 [F/m] 0 410 [H/m] 36 [11] 8 v c 310 m/s 0 120 [] EM wave in Media • Refractive index of a medium is defined as: c velocity of light (EM wave) in vacuum n r r v velocity of light (EM wave) in medium 0 0 [12] r : Relative magnetic permeability r : Relative electric permittivity (r 1) • For non-magnetic media : [13] n r Intensity & power flow of TEM wave 1 • The poynting vector S E H for TEM wave is parallel to the 2 wavevector k so that the power flows along in a direction normal to the wavefront or parallel to k. The magnitude of the poynting vector is the intensity of TEM wave as follows: E 2 I 0 [W/m 2 ] [14] 2 Connection between em wave optics & ray optics • The EM waves radiated by a small optical source can be represented by a train of spherical wave fronts with the source at the center • A wave front is the locus of all points in the wave train which exhibit the same phase • Large scale optical effects such as reflection & refraction can be analyzed by simple geometrical process called ray tracing(geometrical optics) Wave fronts (constant phase surfaces) Wave fronts Wave fronts k P E r rays k P O z A perfect plane wave A perfect spherical wave A divergent beam (a) (b) (c) Examples of possible EM waves Modes in an optical fiber Meridional and Skew rays • Meridional rays: The rays which always pass through the axis of fiber giving high optical intensity at the center of the core of the fiber. • Skew Rays : The rays which never intersect the axis of the fiber, giving low optical intensity at the center and high intensity Meridional and Skew rays Number of fiber modes vs. the V number Limitations of the Ray-model • (1) The ray model gives an impression that during total internal reflection the energy is confined to the core only. However, it is not so. In reality the optical energy spreads in cladding also. • (2) The ray model does not speak of the discrete field patterns for propagation inside a fiber. • (3) The ray model breaks down when the core size becomes comparable to the wavelength of light. The ray model therefore is not quite justified for a SM fiber. • The limitations of the Ray model are overcome in the wave model General form of linearly polarized plane waves Any two orthogonal plane waves Can be combined into a linearly Polarized wave. Conversely, any arbitrary linearly polarized wave can be resolved into two independent Orthogonal plane waves that are in phase. E e x E0x cos(ωt kz) e y E0 y cos(ωt kz) E E E 2 E 2 0x 0 y [15] E tan 1 ( 0 y ) E0x Elliptically Polarized plane waves E e x Ex e y E y e x E0x cos(ωt kz) e y cos(ωt kz ) 2 2 E E E E x y 2 x y cos sin 2 E0x E0 y E0x E0 y [16] 2E0x E0 y cos tan(2) 2 2 E0x E0 y Circularly polarized waves Circular polarizati on : E E E & [17] 0x 0 y 0 2 : right circularly polarized, - : left circularly polarized Laws of Reflection & Refraction Reflection law: angle of incidence=angle of reflection Snell’s law of refraction: n1 sin 1 n2 sin 2 [18] Total internal reflection, Critical angle Transmitted (refracted) light k t 2 90 2 n 2 Evanescent wave n 1 > n2 k k 1 i r 1 c Critical angle 1 c TIR Incident Reflected light light n2 (a) sin c (b) (c) n1 Light wave travelling in a more dense medium strikes a less dense medium. Depending on the incidence anglewrt to c , which is determined by the ratio of the refractive indices, the wave may be transmitted (refracted) or reflected. (a) 1 c and total internal reflection (TIR). (c) (b) 1 c 1 c n2 [19] sin c n1 Phase shift due to TIR • The totally reflected wave experiences a phase shift however which is given by: n 2 cos 2 1 n n2 cos 2 1 tan N 1 ; tan p 1 [20] 2 nsin 1 2 sin 1 n n 1 n2 • Where (p,N) refer to the electric field components parallel or normal to the plane of incidence respectively. Optical wave guiding by TIR: Dielectric Slab Waveguide Propagation mechanism in an ideal step-index optical waveguide. Launching optical rays to slab waveguide n2 sin min ; minimum angle that supports TIR n1 [21] Maximum entrance angle, 0 max is found from the Snell’s relation written at the fiber end face. 2 2 [22] nsin 0max n1 sin c n1 n2 Numerical aperture: 2 2 NA nsin 0 max n1 n2 n1 2 [23] n1 n2 [24] n1 Optical rays transmission through dielectric slab waveguide n n ; 1 2 c 2 c O For TE-case, when electric waves are normal to the plane of incidence must be satisfied with following relationship: 2 2 n d sin m n cos 2 n tan 1 1 2 [25] 2 n sin 1 EM analysis of Slab waveguide • For each particular angle, in which light ray can be faithfully transmitted along slab waveguide, we can obtain one possible propagating wave solution from a Maxwell’s equations or mode. • The modes with electric field perpendicular to the plane of incidence (page) are called TE (Transverse Electric) and numbered as: TE 0 ,TE 1,TE 2 ,... Electric field distribution of these modes for 2D slab waveguide can be expressed as: Em (x, y, z,t) e x f m (y)cos(ωt m z) [26] m 0,1,2,3 (mode number) wave transmission along slab waveguides, fibers & other type of optical waveguides can be fully described by time & z dependency of the mode: j(wtm z) cos(ωt m z) or e TE modes in slab waveguide y z Em (x, y, z,t) e x f m (y)cos(ωt m z) m 0,1,2,3 (mode number) Modes in slab waveguide • The order of the mode is equal to the # of field zeros across the guide. The order of the mode is also related to the angle in which the ray congruence corresponding to this mode makes with the plane of the waveguide (or axis of the fiber). The steeper the angle, the higher the order of the mode. • For higher order modes the fields are distributed more toward the edges of the guide and penetrate further into the cladding region.
Load more

Recommended publications
  • Glossary Physics (I-Introduction)
    1 Glossary Physics (I-introduction) - Efficiency: The percent of the work put into a machine that is converted into useful work output; = work done / energy used [-]. = eta In machines: The work output of any machine cannot exceed the work input (<=100%); in an ideal machine, where no energy is transformed into heat: work(input) = work(output), =100%. Energy: The property of a system that enables it to do work. Conservation o. E.: Energy cannot be created or destroyed; it may be transformed from one form into another, but the total amount of energy never changes. Equilibrium: The state of an object when not acted upon by a net force or net torque; an object in equilibrium may be at rest or moving at uniform velocity - not accelerating. Mechanical E.: The state of an object or system of objects for which any impressed forces cancels to zero and no acceleration occurs. Dynamic E.: Object is moving without experiencing acceleration. Static E.: Object is at rest.F Force: The influence that can cause an object to be accelerated or retarded; is always in the direction of the net force, hence a vector quantity; the four elementary forces are: Electromagnetic F.: Is an attraction or repulsion G, gravit. const.6.672E-11[Nm2/kg2] between electric charges: d, distance [m] 2 2 2 2 F = 1/(40) (q1q2/d ) [(CC/m )(Nm /C )] = [N] m,M, mass [kg] Gravitational F.: Is a mutual attraction between all masses: q, charge [As] [C] 2 2 2 2 F = GmM/d [Nm /kg kg 1/m ] = [N] 0, dielectric constant Strong F.: (nuclear force) Acts within the nuclei of atoms: 8.854E-12 [C2/Nm2] [F/m] 2 2 2 2 2 F = 1/(40) (e /d ) [(CC/m )(Nm /C )] = [N] , 3.14 [-] Weak F.: Manifests itself in special reactions among elementary e, 1.60210 E-19 [As] [C] particles, such as the reaction that occur in radioactive decay.
    [Show full text]
  • 25 Geometric Optics
    CHAPTER 25 | GEOMETRIC OPTICS 887 25 GEOMETRIC OPTICS Figure 25.1 Image seen as a result of reflection of light on a plane smooth surface. (credit: NASA Goddard Photo and Video, via Flickr) Learning Objectives 25.1. The Ray Aspect of Light • List the ways by which light travels from a source to another location. 25.2. The Law of Reflection • Explain reflection of light from polished and rough surfaces. 25.3. The Law of Refraction • Determine the index of refraction, given the speed of light in a medium. 25.4. Total Internal Reflection • Explain the phenomenon of total internal reflection. • Describe the workings and uses of fiber optics. • Analyze the reason for the sparkle of diamonds. 25.5. Dispersion: The Rainbow and Prisms • Explain the phenomenon of dispersion and discuss its advantages and disadvantages. 25.6. Image Formation by Lenses • List the rules for ray tracking for thin lenses. • Illustrate the formation of images using the technique of ray tracking. • Determine power of a lens given the focal length. 25.7. Image Formation by Mirrors • Illustrate image formation in a flat mirror. • Explain with ray diagrams the formation of an image using spherical mirrors. • Determine focal length and magnification given radius of curvature, distance of object and image. Introduction to Geometric Optics Geometric Optics Light from this page or screen is formed into an image by the lens of your eye, much as the lens of the camera that made this photograph. Mirrors, like lenses, can also form images that in turn are captured by your eye. 888 CHAPTER 25 | GEOMETRIC OPTICS Our lives are filled with light.
    [Show full text]
  • Multidisciplinary Design Project Engineering Dictionary Version 0.0.2
    Multidisciplinary Design Project Engineering Dictionary Version 0.0.2 February 15, 2006 . DRAFT Cambridge-MIT Institute Multidisciplinary Design Project This Dictionary/Glossary of Engineering terms has been compiled to compliment the work developed as part of the Multi-disciplinary Design Project (MDP), which is a programme to develop teaching material and kits to aid the running of mechtronics projects in Universities and Schools. The project is being carried out with support from the Cambridge-MIT Institute undergraduate teaching programe. For more information about the project please visit the MDP website at http://www-mdp.eng.cam.ac.uk or contact Dr. Peter Long Prof. Alex Slocum Cambridge University Engineering Department Massachusetts Institute of Technology Trumpington Street, 77 Massachusetts Ave. Cambridge. Cambridge MA 02139-4307 CB2 1PZ. USA e-mail: [email protected] e-mail: [email protected] tel: +44 (0) 1223 332779 tel: +1 617 253 0012 For information about the CMI initiative please see Cambridge-MIT Institute website :- http://www.cambridge-mit.org CMI CMI, University of Cambridge Massachusetts Institute of Technology 10 Miller’s Yard, 77 Massachusetts Ave. Mill Lane, Cambridge MA 02139-4307 Cambridge. CB2 1RQ. USA tel: +44 (0) 1223 327207 tel. +1 617 253 7732 fax: +44 (0) 1223 765891 fax. +1 617 258 8539 . DRAFT 2 CMI-MDP Programme 1 Introduction This dictionary/glossary has not been developed as a definative work but as a useful reference book for engi- neering students to search when looking for the meaning of a word/phrase. It has been compiled from a number of existing glossaries together with a number of local additions.
    [Show full text]
  • 9.2 Refraction and Total Internal Reflection
    9.2 refraction and total internal reflection When a light wave strikes a transparent material such as glass or water, some of the light is reflected from the surface (as described in Section 9.1). The rest of the light passes through (transmits) the material. Figure 1 shows a ray that has entered a glass block that has two parallel sides. The part of the original ray that travels into the glass is called the refracted ray, and the part of the original ray that is reflected is called the reflected ray. normal incident ray reflected ray ␪ ␪i r ␪r ϭ ␪i air glass ␪2 refracted ray Figure 1 A light ray that strikes a glass surface is both reflected and refracted. Refracted and reflected rays of light account for many things that we encounter in our everyday lives. For example, the water in a pool can look shallower than it really is. A stick can look as if it bends at the point where it enters the water. On a hot day, the road ahead can appear to have a puddle of water, which turns out to be a mirage. These effects are all caused by the refraction and reflection of light. refraction The direction of the refracted ray is different from the direction of the incident refraction the bending of light as it ray, an effect called refraction. As with reflection, you can measure the direction of travels at an angle from one medium the refracted ray using the angle that it makes with the normal. In Figure 1, this to another angle is labelled θ2.
    [Show full text]
  • Light Bending and X-Ray Echoes from Behind a Supermassive Black Hole D.R
    Light bending and X-ray echoes from behind a supermassive black hole D.R. Wilkins1*, L.C. Gallo2, E. Costantini3,4, W.N. Brandt5,6,7 and R.D. Blandford1 1Kavli Institute for Particle Astrophysics and Cosmology, Stanford University, 452 Lomita Mall, Stanford, CA 94305, USA 2Department of Astronomy & Physics, Saint Mary’s University, Halifax, NS. B3H 3C3, Canada 3SRON, Netherlands Institute for Space Research, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands 4Anton Pannekoeck Institute for Astronomy, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands 5Department of Astronomy and Astrophysics, 525 Davey Lab, The Pennsylvania State University, University Park, PA 16802, USA 6Institute for Gravitation and the Cosmos, The Pennsylvania State University, University Park, PA 16802, USA 7Department of Physics, 104 Davey Lab, The Pennsylvania State University, University Park, PA 16802, USA *Corresponding author. E-mail: [email protected] Preprint version. Submitted to Nature 14 August 2020, accepted 24 May 2021 The innermost regions of accretion disks around black holes are strongly irradiated by X-rays that are emitted from a highly variable, compact corona, in the immediate vicinity of the black hole [1, 2, 3]. The X-rays that are seen reflected from the disk [4] and the time delays, as variations in the X-ray emission echo or ‘reverberate’ off the disk [5, 6] provide a view of the environment just outside the event horizon. I Zwicky 1 (I Zw 1), is a nearby narrow line Seyfert 1 galaxy [7, 8]. Previous studies of the reverberation of X-rays from its accretion disk revealed that the corona is composed of two components; an extended, slowly varying component over the surface of the inner accretion disk, and a collimated core, with luminosity fluctuations propagating upwards from its base, which dominates the more rapid variability [9, 10].
    [Show full text]
  • Reflections and Refractions in Ray Tracing
    Reflections and Refractions in Ray Tracing Bram de Greve ([email protected]) November 13, 2006 Abstract materials could be air (η ≈ 1), water (20◦C: η ≈ 1.33), glass (crown glass: η ≈ 1.5), ... It does not matter which refractive index is the greatest. All that counts is that η is the refractive When writing a ray tracer, sooner or later you’ll stumble 1 index of the material you come from, and η of the material on the problem of reflection and transmission. To visualize 2 you go to. This (very important) concept is sometimes misun- mirror-like objects, you need to reflect your viewing rays. To derstood. simulate a lens, you need refraction. While most people have heard of the law of reflection and Snell’s law, they often have The direction vector of the incident ray (= incoming ray) is i, difficulties with actually calculating the direction vectors of and we assume this vector is normalized. The direction vec- the reflected and refracted rays. In the following pages, ex- tors of the reflected and transmitted rays are r and t and will actly this problem will be addressed. As a bonus, some Fres- be calculated. These vectors are (or will be) normalized as nel equations will be added to the mix, so you can actually well. We also have the normal vector n, orthogonal to the in- calculate how much light is reflected or transmitted (yes, it’s terface and pointing towards the first material η1. Again, n is possible). At the end, you’ll have some usable formulas to use normalized.
    [Show full text]
  • 4.4 Total Internal Reflection
    n 1:33 sin θ = water sin θ = sin 35◦ ; air n water 1:00 air i.e. ◦ θair = 49:7 : Thus, the height above the horizon is ◦ ◦ θ = 90 θair = 40:3 : (4.7) − Because the sun is far away from the fisherman and the diver, the fisherman will see the sun at the same angle above the horizon. 4.4 Total Internal Reflection Suppose that a light ray moves from a medium of refractive index n1 to one in which n1 > n2, e.g. glass-to-air, where n1 = 1:50 and n2 = 1:0003. ◦ If the angle of incidence θ1 = 10 , then by Snell's law, • n 1:50 θ = sin−1 1 sin θ = sin−1 sin 10◦ 2 n 1 1:0003 2 = sin−1 (0:2604) = 15:1◦ : ◦ If the angle of incidence is θ1 = 50 , then by Snell's law, • n 1:50 θ = sin−1 1 sin θ = sin−1 sin 50◦ 2 n 1 1:0003 2 = sin−1 (1:1487) =??? : ◦ So when θ1 = 50 , we have a problem: Mathematically: the angle θ2 cannot be computed since sin θ2 > 1. • 142 Physically: the ray is unable to refract through the boundary. Instead, • 100% of the light reflects from the boundary back into the prism. This process is known as total internal reflection (TIR). Figure 8672 shows several rays leaving a point source in a medium with re- fractive index n1. Figure 86: The refraction and reflection of light rays with increasing angle of incidence. The medium on the other side of the boundary has n2 < n1.
    [Show full text]
  • GLAST Science Glossary (PDF)
    GLAST SCIENCE GLOSSARY Source: http://glast.sonoma.edu/science/gru/glossary.html Accretion — The process whereby a compact object such as a black hole or neutron star captures matter from a normal star or diffuse cloud. Active galactic nuclei (AGN) — The central region of some galaxies that appears as an extremely luminous point-like source of radiation. They are powered by supermassive black holes accreting nearby matter. Annihilation — The process whereby a particle and its antimatter counterpart interact, converting their mass into energy according to Einstein’s famous formula E = mc2. For example, the annihilation of an electron and positron results in the emission of two gamma-ray photons, each with an energy of 511 keV. Anticoincidence Detector — A system on a gamma-ray observatory that triggers when it detects an incoming charged particle (cosmic ray) so that the telescope will not mistake it for a gamma ray. Antimatter — A form of matter identical to atomic matter, but with the opposite electric charge. Arcminute — One-sixtieth of a degree on the sky. Like latitude and longitude on Earth's surface, we measure positions on the sky in angles. A semicircle that extends up across the sky from the eastern horizon to the western horizon is 180 degrees. One degree, therefore, is not a very big angle. An arcminute is an even smaller angle, 1/60 as large as a degree. The Moon and Sun are each about half a degree across, or about 30 arcminutes. If you take a sharp pencil and hold it at arm's length, then the point of that pencil as seen from your eye is about 3 arcminutes across.
    [Show full text]
  • Refraction • When a Light Ray Moves from One Medium to Another, the Ray Bends
    Refraction • When a light ray moves from one medium to another, the ray bends. – If the second medium has a higher index of refraction than the first, the refracted ray is bent towards the normal relative to the incident ray. Figure 32.21a Snell’s Law nn1sin 1 2 sin 2 Figure 32.21a Consequences of Snell’s Law • When light travels into a medium of higher index of refraction, there is a maximum angle for the refracted ray < 90°. – The incident light from the first medium (e.g. air) is compressed into a cone in the second medium (e.g. water). Figure 32.32a Figure 32.32b Consequences of Snell’s Law • When light travels towards a medium of lower index of refraction, no refracted ray will emerge for incident rays with i > c. – Total Internal Reflection: When this condition is fulfilled, the light ray is completely reflected back into the original medium. Figure 32.31 An air prism is immersed in water. A ray of monochromatic light strikes one face as shown. Which arrow shows the emerging ray? Law of Reflection • When a ray of light hits a reflective surface (e.g. mirror), the incident and reflected rays make the same angle with respect to the normal to the surface. Figure 32.2b Spherical Mirrors • A reflective “portion of a sphere”. • If the mirror is a small enough portion, all light rays parallel to the principal axis (which passes through center C and the middle of the mirror A), will converge on a single focal point F. • The focal length f (distance from mirror to F) is half the radius of the sphere r.
    [Show full text]
  • 23-1 the Ray Model of Light
    23-1 The Ray Model of Light We will start our investigation of geometrical optics (optics based on the geometry of similar triangles) by learning the basics of the ray model of light. We will then apply this model to understand reflection and mirrors, in this chapter, and refraction and lenses, in chapter 24. Using the triangles that result from applying the ray model, we will derive equations we can apply to predict where the image created by a mirror or lens will be formed. A ray is as a narrow beam of light that tends to travel in a straight line. An example of a ray is the beam of light from a laser or laser pointer. In the ray model of light, a ray travels in a straight line until it hits something, like a mirror, or an interface Figure 23.1: The photograph shows rays of light between two different materials. The passing through openings in clouds above the interaction between the light ray and the Washington Monument. Each ray follows a straight mirror or interface generally causes the ray to line. (Photo credit: public-domain photo from change direction, at which point the ray again Wikimedia Commons) travels in a straight line until it encounters something else that causes a change in direction. An example in which the ray model of light applies is shown in Figure 23.1, in which the beams of sunlight travel in straight lines. A laser emits a single ray of light, but we can also apply the ray model in situations in which a light source sends out many rays, in many directions.
    [Show full text]
  • English for Physics Chap.1. Glassary
    English for Physics 1/5 Chap.1. Glassary (Part 1) General and Math 0 Category 単語 Words Definitions/descriptions 1 General 電磁気学 electricity and magnetism 2 General 量子力学 quantum mechanics 3 General 統計力学 statistical mechanics 4 General 卒業論文 senior thesis 5 General 大学院生 graduate student 6 General 学部生 undergraduate student 7 General 理学研究科 Graduate School of Science 8 General 理学部 Faculty of Science 9 General 前期/後期 first semester/ second semester 10 General 経験則 empirical rule A rule derived from experiments or observations rather than theory. The smallest unit into which any substance is divided into without 11 Matter 分子 molecule losing its chemical nature, usually consisting of a group of atoms. The smallest part of an element that can exist, consisting of a small 12 Matter 原子 atom dense nucleus of protons and neutrons surrounded by orbiting electrons. 13 Matter 原子核 nucleus (pl. nuclei) The most massive part of an atom, consisting of protons and neutrons. A collective term for a proton or neutron, i.e. for a constituent of an 14 Matter 核子 nucleon atomic nucleus. 15 Matter 陽子 proton A positively charged nucleon. An elementary particle with zero charge and with rest mass nearly 16 Matter 中性子 neutron equal to that of a proton. A charge-neutral nucleon. A stable elementary particle whose negative charge -e defines an 17 Matter 電子 electron elementary unit of charge. 18 Matter 光子 photon A quantized particle of electromagnetic radiation (light). 19 Matter 水素 hydrogen An element whose atom consists of one proton and one electron. A table of chemical elements arranged in order of their atomic 20 Matter 元素の周期表 periodic table of the elements numbers.
    [Show full text]
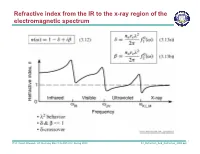
  • Refractive Index from the IR to the X-Ray Region of the Electromagnetic Spectrum
    Refractive index from the IR to the x-ray region of the electromagnetic spectrum 1 Prof. David Attwood / UC Berkeley EE213 & AST210 / Spring 2009 04_Reflection_And_Refraction_2009.ppt Reflection and refraction of EUV/soft x-ray radiation 2 Prof. David Attwood / UC Berkeley EE213 & AST210 / Spring 2009 04_Reflection_And_Refraction_2009.ppt Atomic scattering factors for Carbon (Z = 6) 3 Prof. David Attwood / UC Berkeley EE213 & AST210 / Spring 2009 04_Reflection_And_Refraction_2009.ppt Atomic scattering factors for Silicon (Z = 14) 4 Prof. David Attwood / UC Berkeley EE213 & AST210 / Spring 2009 04_Reflection_And_Refraction_2009.ppt Atomic scattering factors for Molybdenum (Z = 42) 5 Prof. David Attwood / UC Berkeley EE213 & AST210 / Spring 2009 04_Reflection_And_Refraction_2009.ppt Phase velocity and refractive index 6 Prof. David Attwood / UC Berkeley EE213 & AST210 / Spring 2009 04_Reflection_And_Refraction_2009.ppt Phase velocity and refractive index (continued) 7 Prof. David Attwood / UC Berkeley EE213 & AST210 / Spring 2009 04_Reflection_And_Refraction_2009.ppt Phase variation and absorption of propagating waves 8 Prof. David Attwood / UC Berkeley EE213 & AST210 / Spring 2009 04_Reflection_And_Refraction_2009.ppt Intensity and absorption in a material of complex refractive index 9 Prof. David Attwood / UC Berkeley EE213 & AST210 / Spring 2009 04_Reflection_And_Refraction_2009.ppt Phase shift relative to vacuum propagation 10 Prof. David Attwood / UC Berkeley EE213 & AST210 / Spring 2009 04_Reflection_And_Refraction_2009.ppt Reflection and refraction at an interface 11 Prof. David Attwood / UC Berkeley EE213 & AST210 / Spring 2009 04_Reflection_And_Refraction_2009.ppt Boundary conditions at an interface 12 Prof. David Attwood / UC Berkeley EE213 & AST210 / Spring 2009 04_Reflection_And_Refraction_2009.ppt Spatial continuity along the interface 13 Prof. David Attwood / UC Berkeley EE213 & AST210 / Spring 2009 04_Reflection_And_Refraction_2009.ppt Total external reflection of soft x-ray and EUV radiation 14 Prof.
    [Show full text]