A Formal System for Euclid's Elements
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Ethnomathematics and Education in Africa
Copyright ©2014 by Paulus Gerdes www.lulu.com http://www.lulu.com/spotlight/pgerdes 2 Paulus Gerdes Second edition: ISTEG Belo Horizonte Boane Mozambique 2014 3 First Edition (January 1995): Institutionen för Internationell Pedagogik (Institute of International Education) Stockholms Universitet (University of Stockholm) Report 97 Second Edition (January 2014): Instituto Superior de Tecnologias e Gestão (ISTEG) (Higher Institute for Technology and Management) Av. de Namaacha 188, Belo Horizonte, Boane, Mozambique Distributed by: www.lulu.com http://www.lulu.com/spotlight/pgerdes Author: Paulus Gerdes African Academy of Sciences & ISTEG, Mozambique C.P. 915, Maputo, Mozambique ([email protected]) Photograph on the front cover: Detail of a Tonga basket acquired, in January 2014, by the author in Inhambane, Mozambique 4 CONTENTS page Preface (2014) 11 Chapter 1: Introduction 13 Chapter 2: Ethnomathematical research: preparing a 19 response to a major challenge to mathematics education in Africa Societal and educational background 19 A major challenge to mathematics education 21 Ethnomathematics Research Project in Mozambique 23 Chapter 3: On the concept of ethnomathematics 29 Ethnographers on ethnoscience 29 Genesis of the concept of ethnomathematics among 31 mathematicians and mathematics teachers Concept, accent or movement? 34 Bibliography 39 Chapter 4: How to recognize hidden geometrical thinking: 45 a contribution to the development of an anthropology of mathematics Confrontation 45 Introduction 46 First example 47 Second example -

Theon of Alexandria and Hypatia
CREATIVE MATH. 12 (2003), 111 - 115 Theon of Alexandria and Hypatia Michael Lambrou Abstract. In this paper we present the story of the most famous ancient female math- ematician, Hypatia, and her father Theon of Alexandria. The mathematician and philosopher Hypatia flourished in Alexandria from the second part of the 4th century until her violent death incurred by a mob in 415. She was the daughter of Theon of Alexandria, a math- ematician and astronomer, who flourished in Alexandria during the second part of the fourth century. Information on Theon’s life is only brief, coming mainly from a note in the Suda (Suida’s Lexicon, written about 1000 AD) stating that he lived in Alexandria in the times of Theodosius I (who reigned AD 379-395) and taught at the Museum. He is, in fact, the Museum’s last attested member. Descriptions of two eclipses he observed in Alexandria included in his commentary to Ptolemy’s Mathematical Syntaxis (Almagest) and elsewhere have been dated as the eclipses that occurred in AD 364, which is consistent with Suda. Although originality in Theon’s works cannot be claimed, he was certainly immensely influential in the preservation, dissemination and editing of clas- sic texts of previous generations. Indeed, with the exception of Vaticanus Graecus 190 all surviving Greek manuscripts of Euclid’s Elements stem from Theon’s edition. A comparison to Vaticanus Graecus 190 reveals that Theon did not actually change the mathematical content of the Elements except in minor points, but rather re-wrote it in Koini and in a form more suitable for the students he taught (some manuscripts refer to Theon’s sinousiai). -

A Conceptual Framework for Investigating Organizational Control and Resistance in Crowd-Based Platforms
Proceedings of the 50th Hawaii International Conference on System Sciences | 2017 A Conceptual Framework for Investigating Organizational Control and Resistance in Crowd-Based Platforms David A. Askay California Polytechnic State University [email protected] Abstract Crowd-based platforms coordinate action through This paper presents a research agenda for crowd decomposing tasks and encouraging individuals to behavior research by drawing from the participate by providing intrinsic (e.g., fun, organizational control literature. It addresses the enjoyment) and/or extrinsic (e.g., status, money, need for research into the organizational and social social interaction, etc.) motivators [3]. Three recent structures that guide user behavior and contributions Information Systems (IS) reviews of crowdsourcing in crowd-based platforms. Crowd behavior is research [6, 4, 7] emphasize the importance of situated within a conceptual framework of designing effective incentive systems. However, organizational control. This framework helps research on motivation is somewhat disparate, with scholars more fully articulate the full range of various categorizations and often inconsistent control mechanisms operating in crowd-based findings as to which incentives are the most effective platforms, contextualizes these mechanisms into the [4]. Moreover, this approach can be limited by its context of crowd-based platforms, challenges existing often deterministic and rational assumptions of user rational assumptions about incentive systems, and behavior and motivation, which overlooks normative clarifies theoretical constructs of organizational and social aspects of human behavior [8]. To more control to foster stronger integration between fully understand the dynamics of crowd behavior and information systems research and organizational and governance of crowd-based projects, IS researchers management science. -
Golden Ratio: a Subtle Regulator in Our Body and Cardiovascular System?
See discussions, stats, and author profiles for this publication at: https://www.researchgate.net/publication/306051060 Golden Ratio: A subtle regulator in our body and cardiovascular system? Article in International journal of cardiology · August 2016 DOI: 10.1016/j.ijcard.2016.08.147 CITATIONS READS 8 266 3 authors, including: Selcuk Ozturk Ertan Yetkin Ankara University Istinye University, LIV Hospital 56 PUBLICATIONS 121 CITATIONS 227 PUBLICATIONS 3,259 CITATIONS SEE PROFILE SEE PROFILE Some of the authors of this publication are also working on these related projects: microbiology View project golden ratio View project All content following this page was uploaded by Ertan Yetkin on 23 August 2019. The user has requested enhancement of the downloaded file. International Journal of Cardiology 223 (2016) 143–145 Contents lists available at ScienceDirect International Journal of Cardiology journal homepage: www.elsevier.com/locate/ijcard Review Golden ratio: A subtle regulator in our body and cardiovascular system? Selcuk Ozturk a, Kenan Yalta b, Ertan Yetkin c,⁎ a Abant Izzet Baysal University, Faculty of Medicine, Department of Cardiology, Bolu, Turkey b Trakya University, Faculty of Medicine, Department of Cardiology, Edirne, Turkey c Yenisehir Hospital, Division of Cardiology, Mersin, Turkey article info abstract Article history: Golden ratio, which is an irrational number and also named as the Greek letter Phi (φ), is defined as the ratio be- Received 13 July 2016 tween two lines of unequal length, where the ratio of the lengths of the shorter to the longer is the same as the Accepted 7 August 2016 ratio between the lengths of the longer and the sum of the lengths. -

Alexandrea Ad Aegyptvm the Legacy of Multiculturalism in Antiquity
Alexandrea ad aegyptvm the legacy of multiculturalism in antiquity editors rogério sousa maria do céu fialho mona haggag nuno simões rodrigues Título: Alexandrea ad Aegyptum – The Legacy of Multiculturalism in Antiquity Coord.: Rogério Sousa, Maria do Céu Fialho, Mona Haggag e Nuno Simões Rodrigues Design gráfico: Helena Lobo Design | www.hldesign.pt Revisão: Paula Montes Leal Inês Nemésio Obra sujeita a revisão científica Comissão científica: Alberto Bernabé, Universidade Complutense de Madrid; André Chevitarese, Universidade Federal, Rio de Janeiro; Aurélio Pérez Jiménez, Universidade de Málaga; Carmen Leal Soares, Universidade de Coimbra; Fábio Souza Lessa, Universidade Federal, Rio de Janeiro; José Augusto Ramos, Universidade de Lisboa; José Luís Brandão, Universidade de Coimbra; Natália Bebiano Providência e Costa, Universidade de Coimbra; Richard McKirahan, Pomona College, Claremont Co-edição: CITCEM – Centro de Investigação Transdisciplinar «Cultura, Espaço e Memória» Via Panorâmica, s/n | 4150-564 Porto | www.citcem.org | [email protected] CECH – Centro de Estudos Clássicos e Humanísticos | Largo da Porta Férrea, Universidade de Coimbra Alexandria University | Cornice Avenue, Shabty, Alexandria Edições Afrontamento , Lda. | Rua Costa Cabral, 859 | 4200-225 Porto www.edicoesafrontamento.pt | [email protected] N.º edição: 1152 ISBN: 978-972-36-1336-0 (Edições Afrontamento) ISBN: 978-989-8351-25-8 (CITCEM) ISBN: 978-989-721-53-2 (CECH) Depósito legal: 366115/13 Impressão e acabamento: Rainho & Neves Lda. | Santa Maria da Feira [email protected] Distribuição: Companhia das Artes – Livros e Distribuição, Lda. [email protected] Este trabalho é financiado por Fundos Nacionais através da FCT – Fundação para a Ciência e Tecnologia no âmbito do projecto PEst-OE/HIS/UI4059/2011 HYPATIA AND THE IDIOSCYNCRASIES OF CHRISTIANITY IN EGYPT – A STUDY OF THE EVENTS OCCURRED AT EASTER 415 A.D. -

On Mathematics As Sense- Making: an Informalattack on the Unfortunate Divorce of Formal and Informal Mathematics
On Mathematics as Sense Making: An InformalAttack On the Unfortunate Divorce of Formal and Informal 16 Mathematics Alan H. Schoenfeld The University of California-Berkeley This chapter explores the ways that mathematics is understood and used in our culture and the role that schooling plays in shaping those mathematical under standings. One of its goals is to blur the boundaries between forma] and informal mathematics: to indicate that, in real mathematical thinking, formal and informal reasoning are deeply intertwined. I begin, however, by briefly putting on the formalist's hat and defining formal reasoning. As any formalist will tell you, it helps to know what the boundaries are before you try to blur them. PROLOGUE: ON THE LIMITS AND PURITY OF FORMAL REASONING QUA FORMAL REASONING To get to the heart of the matter, formal systems do not denote; that is, formal systems in mathematics are not about anything. Formal systems consist of sets of symbols and rules for manipulating them. As long as you play by the rules, the results are valid within the system. But if you try to apply these systems to something from the real world (or something else), you no longer engage in formal reasoning. You are applying the mathematics at that point. Caveat emp tor: the end result is only as good as the application process. Perhaps the clearest example is geometry. Insofar as most people are con cerned, the plane or solid (Euclidean) geometry studied in secondary school provides a mathematical description of the world they live in and of the way the world must be. -

Mathematics in Informal Learning Environments: a Summary of the Literature
MATHEMATICS IN INFORMAL LEARNING ENVIRONMENTS: A SUMMARY OF THE LITERATURE Scott Pattison, Andee Rubin, Tracey Wright Updated March 2017 Research on mathematical reasoning and learning has long been a central part of the classroom and formal education literature (e.g., National Research Council, 2001, 2005). However, much less attention has been paid to how children and adults engage with and learn about math outside of school, including everyday settings and designed informal learning environments, such as interactive math exhibits in science centers. With the growing recognition of the importance of informal STEM education (National Research Council, 2009, 2015), researchers, educators, and policymakers are paying more attention to how these experiences might support mathematical thinking and learning and contribute to the broader goal of ensuring healthy, sustainable, economically vibrant communities in this increasingly STEM-rich world. To support these efforts, we conducted a literature review of research on mathematical thinking and learning outside the classroom, in everyday settings and designed informal learning environments. This work was part of the NSF-funded Math in the Making project, led by TERC and the Institute for Learning Innovation and designed to advance researchers’ and educators’ understanding of how to highlight and enhance the mathematics in making experiences.1 Recognizing that the successful integration of mathematics and making requires an understanding of how individuals engage with math in these informal learning environments, we gathered and synthesized the informal mathematics education literature, with the hope that findings would support the Math in the Making project and inform the work of mathematics researchers and educators more broadly. -

Effective Strategies for Promoting Informal Mathematics Learning
Access Algebra: Effective Strategies for Promoting Informal Mathematics Learning Prepared for by Lynn Dierking Michael Dalton Jennifer Bachman Oregon State University 2008 with the generous support of This material is based upon work supported by the National Science Foundation under grant Number DRL-0714634. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation or the Oregon Museum of Science and Industry. © OREGON MUSEUM OF SCIENCE AND INDUSTRY, September 2011 Access Algebra: Effective Strategies for Promoting Informal Mathematics Learning Prepared for the Oregon Museum of Science and Industry Oregon State University Lynn Dierking * Michael Dalton * Jennifer Bachman Executive Summary The Oregon Museum of Science and Industry (OMSI) received a five- year grant from the National Science Foundation (NSF) to develop the Access Algebra: Effective Strategies for Promoting Informal Mathematics Learning project. Access Algebra will include a traveling exhibition and a comprehensive professional development program for educational staff at host museums. Access Algebra will target middle- school age youth and engage visitors in design activities that promote creativity and innovation and build mathematics literacy by taking a non-traditional, experiential approach to mathematics learning. Oregon State University (OSU) faculty from the College of Education and the College of Science with expertise in mathematics teaching, administrative experience at K–20 levels and within the Oregon Department of Education, and in free-choice learning settings and research are collaborating on research and development for the exhibit prototypes and professional development components of the project. -

Thales of Miletus Sources and Interpretations Miletli Thales Kaynaklar Ve Yorumlar
Thales of Miletus Sources and Interpretations Miletli Thales Kaynaklar ve Yorumlar David Pierce October , Matematics Department Mimar Sinan Fine Arts University Istanbul http://mat.msgsu.edu.tr/~dpierce/ Preface Here are notes of what I have been able to find or figure out about Thales of Miletus. They may be useful for anybody interested in Thales. They are not an essay, though they may lead to one. I focus mainly on the ancient sources that we have, and on the mathematics of Thales. I began this work in preparation to give one of several - minute talks at the Thales Meeting (Thales Buluşması) at the ruins of Miletus, now Milet, September , . The talks were in Turkish; the audience were from the general popu- lation. I chose for my title “Thales as the originator of the concept of proof” (Kanıt kavramının öncüsü olarak Thales). An English draft is in an appendix. The Thales Meeting was arranged by the Tourism Research Society (Turizm Araştırmaları Derneği, TURAD) and the office of the mayor of Didim. Part of Aydın province, the district of Didim encompasses the ancient cities of Priene and Miletus, along with the temple of Didyma. The temple was linked to Miletus, and Herodotus refers to it under the name of the family of priests, the Branchidae. I first visited Priene, Didyma, and Miletus in , when teaching at the Nesin Mathematics Village in Şirince, Selçuk, İzmir. The district of Selçuk contains also the ruins of Eph- esus, home town of Heraclitus. In , I drafted my Miletus talk in the Math Village. Since then, I have edited and added to these notes. -

The Holy Spirit and the Physical Uníverse: the Impact of Scjentific Paradigm Shifts on Contemporary Pneumatology
Theological Studies 70 (2009) . THE HOLY SPIRIT AND THE PHYSICAL UNÍVERSE: THE IMPACT OF SCJENTIFIC PARADIGM SHIFTS ON CONTEMPORARY PNEUMATOLOGY WOLFGANG VONDEY A methodological shift occurred in the sciences in the 20th century that has irreversible repercussions for a contemporary theology of the Holy Spirit. Newton and Einstein followed fundamentally different trajectories that provide radically dissimilar frame- works for the pneumatological endeavor. Pneumatology after Einstein is located in a different cosmological framework constituted by the notions of order, rationality, relationality, symmetry, and movement. These notions provide the immediate challenges to a contemporary understanding of the Spirit in the physical universe. HPHE PARADIGM SHIFT IN SCIENCE from Ptolemaic to Copernican cosmo- Â logy is clearly reflected in post-Enlightenment theology. The wide- ranging implications of placing the sun instead of the earth at the center of the universe marked the beginnings of both the scientific and religious revolutions of the 16th century. A century later, Isaac Newton provided for the first time a comprehensive system of physical causality that heralded space and time as the absolute constituents of experiential reality from the perspective of both natural philosophy and theology.^ Despite the echoes WOLFGANG VONDEY received his Ph.D. in systematic theology and ethics at Marquette University and is currently associate professor of systematic theology in the School of Divinity, Regent University, Virginia. A prolific writer on Pneu- matology, ecclesiology, and the dialogue of science and theology, he has most recently published: People of Bread: Rediscovering Ecclesiology (2008); "Pentecos- tal Perspectives on The Nature and Mission of the Church" in "The Nature and Mission of the Church": Ecclesial Reality and Ecumenical Horizons for the Twenty- First Century, ed. -

The Philosophy of Mathematics Education
The Philosophy of Mathematics Education The Philosophy of Mathematics Education Paul Ernest © Paul Ernest 1991 All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without permission in writing from the copyright holder and the Publisher. First published 1991 This edition published in the Taylor & Francis e-Library, 2004. RoutledgeFalmer is an imprint of the Taylor & Francis Group British Library Cataloguing in Publication Data Ernest, Paul The philosophy of mathematics education. 1. Education. Curriculum subjects: Mathematics. Teaching. I. Title 510.7 ISBN 0-203-49701-5 Master e-book ISBN ISBN 0-203-55790-5 (Adobe eReader Format) ISBN 1-85000-666-0 (Print Edition) ISBN 1-85000-667-9 pbk Library of Congress Cataloging-in-Publication Data is available on request Contents List of Tables and Figures viii Acknowledgments ix Introduction xi Rationale xi The Philosophy of Mathematics Education xii This Book xiv Part 1 The Philosophy of Mathematics 1 1 A Critique of Absolutist Philosophies of Mathematics 3 Introduction 3 The Philosophy of Mathematics 3 The Nature of Mathematical Knowledge 4 The Absolutist View of Mathematical Knowledge 7 The Fallacy of Absolutism 13 The Fallibilist Critique of Absolutism 15 The Fallibilist View 18 Conclusion 20 2 The Philosophy of Mathematics Reconceptualized 23 The Scope of the Philosophy of Mathematics 23 A Further Examination of Philosophical Schools 27 Quasi-empiricism -
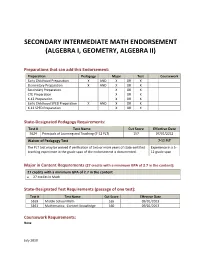
Secondary Intermediate Math Endorsement (Algebra I, Geometry, Algebra Ii)
SECONDARY INTERMEDIATE MATH ENDORSEMENT (ALGEBRA I, GEOMETRY, ALGEBRA II) Preparations that can add this Endorsement: Preparation Pedagogy Major Test Coursework Early Childhood Preparation X AND X OR X Elementary Preparation X AND X OR X Secondary Preparation X OR X CTE Preparation X OR X K-12 Preparation X OR X Early Childhood SPED Preparation X AND X OR X K-12 SPED Preparation X OR X State-Designated Pedagogy Requirements: Test # Test Name Cut Score Effective Date 5624 Principals of Learning and Teaching (7-12 PLT) 157 07/01/2012 Waiver of Pedagogy Test 7-12 PLT The PLT test may be waived if verification of two or more years of state-certified Experience in a 5- teaching experience in the grade span of the endorsement is documented. 12 grade span Major in Content Requirements (27 credits with a minimum GPA of 2.7 in the content): 27 credits with a minimum GPA of 2.7 in the content • 27 credits in Math State-Designated Test Requirements (passage of one test): Test # Test Name Cut Score Effective Date 5169 Middle School Math 165 09/01/2013 5161 Mathematics: Content Knowledge 160 09/01/2013 Coursework Requirements: None July 2019 Intermediate Math Endorsement Page 2 Assignment Codes: Code Assignment Description 02001 Informal Mathematics 02002 General Math 02035 Math, Grade 5 02036 Math, Grade 6 02037 Math, Grade 7 02038 Math, Grade 8 02039 Grades 5-8 Math 02040 Grades 5-8 Pre-Algebra 02051 Pre-Algebra I 02052 Algebra I 02053 Algebra I - Part 1 02054 Algebra I - Part 2 02055 Transition Algebra 02056 Algebra II 02062 Integrated Mathematics