The Philosophy of Mathematics Education
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Case Study Exploring the Nature of How Prekindergarten Teachers’ Mathematics Instruction Decisions Relate to Their Mathematics Pedagogical Content Knowledge
Old Dominion University ODU Digital Commons Teaching & Learning Theses & Dissertations Teaching & Learning Spring 2020 A Case Study Exploring the Nature of How Prekindergarten Teachers’ Mathematics Instruction Decisions Relate to Their Mathematics Pedagogical Content Knowledge Raleta Summers Dawkins Old Dominion University, [email protected] Follow this and additional works at: https://digitalcommons.odu.edu/teachinglearning_etds Part of the Early Childhood Education Commons, Science and Mathematics Education Commons, and the Teacher Education and Professional Development Commons Recommended Citation Dawkins, Raleta S.. "A Case Study Exploring the Nature of How Prekindergarten Teachers’ Mathematics Instruction Decisions Relate to Their Mathematics Pedagogical Content Knowledge" (2020). Doctor of Philosophy (PhD), Dissertation, Teaching & Learning, Old Dominion University, DOI: 10.25777/63kg-gz86 https://digitalcommons.odu.edu/teachinglearning_etds/61 This Dissertation is brought to you for free and open access by the Teaching & Learning at ODU Digital Commons. It has been accepted for inclusion in Teaching & Learning Theses & Dissertations by an authorized administrator of ODU Digital Commons. For more information, please contact [email protected]. A CASE STUDY EXPLORING THE NATURE OF HOW PREKINDERGARTEN TEACHERS’ MATHEMATICS INSTRUCTION DECISIONS RELATE TO THEIR MATHEMATICS PEDAGOGICAL CONTENT KNOWLEDGE by Raleta Summers Dawkins B.S. December 2004, North Carolina Agricultural & Technical State University M.A. Ed. December 2008, -

Ethnomathematics and Education in Africa
Copyright ©2014 by Paulus Gerdes www.lulu.com http://www.lulu.com/spotlight/pgerdes 2 Paulus Gerdes Second edition: ISTEG Belo Horizonte Boane Mozambique 2014 3 First Edition (January 1995): Institutionen för Internationell Pedagogik (Institute of International Education) Stockholms Universitet (University of Stockholm) Report 97 Second Edition (January 2014): Instituto Superior de Tecnologias e Gestão (ISTEG) (Higher Institute for Technology and Management) Av. de Namaacha 188, Belo Horizonte, Boane, Mozambique Distributed by: www.lulu.com http://www.lulu.com/spotlight/pgerdes Author: Paulus Gerdes African Academy of Sciences & ISTEG, Mozambique C.P. 915, Maputo, Mozambique ([email protected]) Photograph on the front cover: Detail of a Tonga basket acquired, in January 2014, by the author in Inhambane, Mozambique 4 CONTENTS page Preface (2014) 11 Chapter 1: Introduction 13 Chapter 2: Ethnomathematical research: preparing a 19 response to a major challenge to mathematics education in Africa Societal and educational background 19 A major challenge to mathematics education 21 Ethnomathematics Research Project in Mozambique 23 Chapter 3: On the concept of ethnomathematics 29 Ethnographers on ethnoscience 29 Genesis of the concept of ethnomathematics among 31 mathematicians and mathematics teachers Concept, accent or movement? 34 Bibliography 39 Chapter 4: How to recognize hidden geometrical thinking: 45 a contribution to the development of an anthropology of mathematics Confrontation 45 Introduction 46 First example 47 Second example -

Extended Instruction in Business Courses to Enhance Student Achievement in Math Lessie Mcnabb Houseworth Walden University
Walden University ScholarWorks Walden Dissertations and Doctoral Studies Walden Dissertations and Doctoral Studies Collection 2015 Extended Instruction in Business Courses to Enhance Student Achievement in Math Lessie McNabb Houseworth Walden University Follow this and additional works at: https://scholarworks.waldenu.edu/dissertations Part of the Other Education Commons, and the Science and Mathematics Education Commons This Dissertation is brought to you for free and open access by the Walden Dissertations and Doctoral Studies Collection at ScholarWorks. It has been accepted for inclusion in Walden Dissertations and Doctoral Studies by an authorized administrator of ScholarWorks. For more information, please contact [email protected]. Walden University COLLEGE OF EDUCATION This is to certify that the doctoral study by Lessie Houseworth has been found to be complete and satisfactory in all respects, and that any and all revisions required by the review committee have been made. Review Committee Dr. Calvin Lathan, Committee Chairperson, Education Faculty Dr. Jennifer Brown, Committee Member, Education Faculty Dr. Amy Hanson, University Reviewer, Education Faculty Chief Academic Officer Eric Riedel, Ph.D. Walden University 2015 Abstract Extended Instruction in Business Courses to Enhance Student Achievement in Math by Lessie M. Houseworth EdS, Walden University, 2010 MS, Indiana University, 1989 BS, Indiana University, 1976 Doctoral Study Submitted in Partial Fulfillment of the Requirements for the Degree of Doctor of Education Walden University March 2015 Abstract Poor achievement on standardized math tests negatively impacts high school graduation rates. The purpose of this quantitative study was to investigate if math instruction in business classes could improve student achievement in math. As supported by constructivist theory, the students in this study were encouraged to use prior knowledge and experiences to make new connections between math concepts and business applications. -

Mathematics Education
MTHE—Mathematics Education 899 Master's Thesis Research MATHEMATICS MTHE Fall, Spring, Summer. 1 to 8 credits. A stu- EDUCATION dent may earn a maximum of 36 credits in all enrollments for this course. R: Open to masters students in the Mathematics Edu- Program in Mathematics Education cation Major. Approval of department. College of Natural Science Master's thesis research. 430 History of Mathematics 926 Proseminar in Mathematics Education I Spring. 3(3-0) P: MTH 133 and MTH 301 Fall of odd years. 3(3-0) Interdepartmental SA: SME 430 with Counseling, Educational Psychology Development of mathematical thought from ancient and Special Education and Mathematics times to the present, selected from Egyptian, Baby- and Teacher Education. Administered by lonian, Mayan, Greek, Indian, and Arab contribu- Mathematics Education. SA: SME 926 tions to mathematics and to the context of today's Research on the learning and teaching of mathe- school mathematics curriculum. matics. Focus on curriculum, discourse, equity and teacher education. 800 Problems in Mathematics for Teachers Fall, Spring, Summer. 1 to 5 credits. A stu- 927 Proseminar in Mathematics Education II dent may earn a maximum of 15 credits in Fall of even years. 3(3-0) Interdepartmental all enrollments for this course. RB: Elemen- with Counseling, Educational Psychology tary Certification or Secondary Certification and Special Education and Mathematics in Mathematics Education R: Open to grad- and Teacher Education. Administered by uate students in the Mathematics Education Mathematics Education. SA: SME 927 Major. Approval of department. Research on the learning and teaching of mathe- Supervised study of problems or issues in mathe- matics. -

History and Pedagogy of Mathematics in Mathematics Education: History of the Field, the Potential of Current Examples, and Directions for the Future Kathleen Clark
History and pedagogy of mathematics in mathematics education: History of the field, the potential of current examples, and directions for the future Kathleen Clark To cite this version: Kathleen Clark. History and pedagogy of mathematics in mathematics education: History of the field, the potential of current examples, and directions for the future. Eleventh Congress of the European Society for Research in Mathematics Education, Utrecht University, Feb 2019, Utrecht, Netherlands. hal-02436281 HAL Id: hal-02436281 https://hal.archives-ouvertes.fr/hal-02436281 Submitted on 12 Jan 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. History and pedagogy of mathematics in mathematics education: History of the field, the potential of current examples, and directions for the future Kathleen M. Clark Florida State University, School of Teacher Education, Tallahassee, Florida USA; [email protected] The field of history of mathematics in mathematics education—often referred to as the history and pedagogy of mathematics domain (or, HPM domain)—can be characterized by an interesting and rich past and a vibrant and promising future. In this plenary, I describe highlights from the development of the field, and in doing so, I focus on several ways in which research in the field of history of mathematics in mathematics education offers important connections to frameworks and areas of long-standing interest within mathematics education research, with a particular emphasis on student learning. -

On Mathematics As Sense- Making: an Informalattack on the Unfortunate Divorce of Formal and Informal Mathematics
On Mathematics as Sense Making: An InformalAttack On the Unfortunate Divorce of Formal and Informal 16 Mathematics Alan H. Schoenfeld The University of California-Berkeley This chapter explores the ways that mathematics is understood and used in our culture and the role that schooling plays in shaping those mathematical under standings. One of its goals is to blur the boundaries between forma] and informal mathematics: to indicate that, in real mathematical thinking, formal and informal reasoning are deeply intertwined. I begin, however, by briefly putting on the formalist's hat and defining formal reasoning. As any formalist will tell you, it helps to know what the boundaries are before you try to blur them. PROLOGUE: ON THE LIMITS AND PURITY OF FORMAL REASONING QUA FORMAL REASONING To get to the heart of the matter, formal systems do not denote; that is, formal systems in mathematics are not about anything. Formal systems consist of sets of symbols and rules for manipulating them. As long as you play by the rules, the results are valid within the system. But if you try to apply these systems to something from the real world (or something else), you no longer engage in formal reasoning. You are applying the mathematics at that point. Caveat emp tor: the end result is only as good as the application process. Perhaps the clearest example is geometry. Insofar as most people are con cerned, the plane or solid (Euclidean) geometry studied in secondary school provides a mathematical description of the world they live in and of the way the world must be. -

Problematizing the Philosophy of Mathematics in a Time of Curriculum Reform Kimberly White-Fredette
The Mathematics Educator 2009/2010, Vol. 19, No. 2, 21–31 Why Not Philosophy? Problematizing the Philosophy of Mathematics in a Time of Curriculum Reform Kimberly White-Fredette This article argues that, as teachers struggle to implement curriculum reform in mathematics, an explicit discussion of philosophy of mathematics is missing from the conversation. Building on the work of Ernest (1988, 1991, 1994, 1998, 1999, 2004), Lerman (1990, 1998, 1999), the National Council of Teachers of Mathematics (1989, 1991, 2000), Davis and Hersh (1981), Hersh (1997), Lakatos (1945/1976), Kitcher (1984), and others, the author draws parallels between social constructivism and a humanism philosophy of mathematics. While practicing mathematicians may be entrenched in a traditional, Platonic philosophy of mathematics, and mathematics education researchers have embraced the fallibilist, humanist philosophy of mathematics (Sfard, 1998), the teachers of school mathematics are caught somewhere in the middle. Mathematics teachers too often hold true to the traditional view of mathematics as an absolute truth independent of human subjectivity. At the same time, they are pushed to teach mathematics as a social construction, an activity that makes sense only through its usefulness. Given these dichotomous views of mathematics, without an explicit conversation about and exploration of the philosophy of mathematics, reform in the teaching and learning of mathematics may be certain to fail. The teaching and learning of mathematics is without a radical change in instructional practices going through tremendous changes. The National and an equally radical change in teachers’ views of Council of Teachers of Mathematics’ (NCTM, 2000) mathematics teaching and learning, as well as the Principles and Standards for School Mathematics discipline of mathematics itself. -

Mathematics in Informal Learning Environments: a Summary of the Literature
MATHEMATICS IN INFORMAL LEARNING ENVIRONMENTS: A SUMMARY OF THE LITERATURE Scott Pattison, Andee Rubin, Tracey Wright Updated March 2017 Research on mathematical reasoning and learning has long been a central part of the classroom and formal education literature (e.g., National Research Council, 2001, 2005). However, much less attention has been paid to how children and adults engage with and learn about math outside of school, including everyday settings and designed informal learning environments, such as interactive math exhibits in science centers. With the growing recognition of the importance of informal STEM education (National Research Council, 2009, 2015), researchers, educators, and policymakers are paying more attention to how these experiences might support mathematical thinking and learning and contribute to the broader goal of ensuring healthy, sustainable, economically vibrant communities in this increasingly STEM-rich world. To support these efforts, we conducted a literature review of research on mathematical thinking and learning outside the classroom, in everyday settings and designed informal learning environments. This work was part of the NSF-funded Math in the Making project, led by TERC and the Institute for Learning Innovation and designed to advance researchers’ and educators’ understanding of how to highlight and enhance the mathematics in making experiences.1 Recognizing that the successful integration of mathematics and making requires an understanding of how individuals engage with math in these informal learning environments, we gathered and synthesized the informal mathematics education literature, with the hope that findings would support the Math in the Making project and inform the work of mathematics researchers and educators more broadly. -

Effective Strategies for Promoting Informal Mathematics Learning
Access Algebra: Effective Strategies for Promoting Informal Mathematics Learning Prepared for by Lynn Dierking Michael Dalton Jennifer Bachman Oregon State University 2008 with the generous support of This material is based upon work supported by the National Science Foundation under grant Number DRL-0714634. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation or the Oregon Museum of Science and Industry. © OREGON MUSEUM OF SCIENCE AND INDUSTRY, September 2011 Access Algebra: Effective Strategies for Promoting Informal Mathematics Learning Prepared for the Oregon Museum of Science and Industry Oregon State University Lynn Dierking * Michael Dalton * Jennifer Bachman Executive Summary The Oregon Museum of Science and Industry (OMSI) received a five- year grant from the National Science Foundation (NSF) to develop the Access Algebra: Effective Strategies for Promoting Informal Mathematics Learning project. Access Algebra will include a traveling exhibition and a comprehensive professional development program for educational staff at host museums. Access Algebra will target middle- school age youth and engage visitors in design activities that promote creativity and innovation and build mathematics literacy by taking a non-traditional, experiential approach to mathematics learning. Oregon State University (OSU) faculty from the College of Education and the College of Science with expertise in mathematics teaching, administrative experience at K–20 levels and within the Oregon Department of Education, and in free-choice learning settings and research are collaborating on research and development for the exhibit prototypes and professional development components of the project. -

Technology and Math
The Effectiveness of Educational Technology Applications for Enhancing Mathematics Achievement in K-12 Classrooms: A Meta-Analysis Alan C. K. Cheung Johns Hopkins University Robert E. Slavin Johns Hopkins University and University of York July, 2011 1 The Best Evidence Encyclopedia is a free web site created by the Johns Hopkins University School of Education’s Center for Data-Driven Reform in Education (CDDRE) under funding from the Institute of Education Sciences, U.S. Department of Education. Introduction According to a recently released report by the U.S. Department of Education (SETDA, 2010), American teenagers are still trailing behind their counterparts in other industrialized countries in their academic performance, especially in mathematics. In the most recent PISA assessments, U.S. 15-year-olds had an average mathematics score below the average of countries in the Organization for Economic Cooperation and Development (OECD). Among the 33 other OECD countries, over half had higher average scores than the U.S., 5 had lower average scores, and 11 had average scores that were not substantially different than the U.S. Similar patterns were found in tests given in 2003 and 2006. Importantly, the problem of students’ performance in mathematics is not equally distributed. While many middle class schools in the U.S. do perform at world class standards, poor and minority students are much less likely to do so. On the 2009 National Assessment of Educational Progress (NAEP, 2009), only 17% of eighth graders eligible for free lunch scored at proficient or better, while 45% of middle class students scored this well. Among African American students, only 12% scored proficient or better, and the percentages were 17% for Hispanics and 18% for American Indians, compared to 44% for Whites and 54% for Asian- Americans. -

Emily Peterek Bonner, Ph.D
Emily P. Bonner Emily Peterek Bonner, Ph.D. The University of Texas at San Antonio College of Education and Human Development Department of Interdisciplinary Learning and Teaching One UTSA Circle San Antonio, TX 78249 Phone: (210) 458-5402 Fax: (210) 458-7281 Office: MB 2.226 [email protected] EDUCATIONAL BACKGROUND 2009: Ph.D., Curriculum and Instruction (Mathematics Education) School of Teaching and Learning, College of Education University of Florida, Gainesville, FL 2002: M.A.T., Secondary Education/Special Education Trinity University, San Antonio, TX 2001: B.A., Mathematics Trinity University, San Antonio, TX PROFESSIONAL EMPLOYMENT HISTORY 2019 – Present: The University of Texas at San Antonio, San Antonio, TX Assistant Dean of Research College of Education and Human Development 2015 – Present: The University of Texas at San Antonio, San Antonio, TX Associate Professor Curriculum and Instruction, Mathematics Education Department of Interdisciplinary Learning and Teaching 2009 – 2015: The University of Texas at San Antonio, San Antonio, TX Assistant Professor Curriculum and Instruction, Mathematics Education Department of Interdisciplinary Learning and Teaching 2005 – 2006: The University of Florida, Gainesville, FL Research Assistant, Project TALL Math: Teachers as Learners Learning Mathematics (PI: Thomasenia Lott Adams, Ph.D.) 1 Emily P. Bonner 2005 – 2009: The University of Florida, Gainesville, FL Graduate Research Assistant and Teaching Assistant College of Education, School of Teaching and Learning 2002 – 2005: Westside High School, Houston, TX Mathematics Teacher AWARDS AND HONORS • Nominee, Richard S. Howe Outstanding Undergraduate Teaching Award, 2020 • Leadership UTSA Cohort, 2016-2017 • Nominated for Regents’ Outstanding Teaching Award (Tenured), 2016, System Level • Nominated for DOCUmation cash award, 2014 • University of Florida Alumni Fellow, 2005-2009 • University of Florida (university-wide) Graduate Student Teaching Award, 2008 • Elizabeth & William F. -
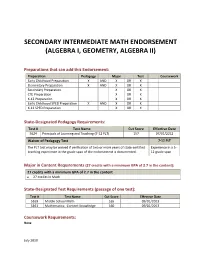
Secondary Intermediate Math Endorsement (Algebra I, Geometry, Algebra Ii)
SECONDARY INTERMEDIATE MATH ENDORSEMENT (ALGEBRA I, GEOMETRY, ALGEBRA II) Preparations that can add this Endorsement: Preparation Pedagogy Major Test Coursework Early Childhood Preparation X AND X OR X Elementary Preparation X AND X OR X Secondary Preparation X OR X CTE Preparation X OR X K-12 Preparation X OR X Early Childhood SPED Preparation X AND X OR X K-12 SPED Preparation X OR X State-Designated Pedagogy Requirements: Test # Test Name Cut Score Effective Date 5624 Principals of Learning and Teaching (7-12 PLT) 157 07/01/2012 Waiver of Pedagogy Test 7-12 PLT The PLT test may be waived if verification of two or more years of state-certified Experience in a 5- teaching experience in the grade span of the endorsement is documented. 12 grade span Major in Content Requirements (27 credits with a minimum GPA of 2.7 in the content): 27 credits with a minimum GPA of 2.7 in the content • 27 credits in Math State-Designated Test Requirements (passage of one test): Test # Test Name Cut Score Effective Date 5169 Middle School Math 165 09/01/2013 5161 Mathematics: Content Knowledge 160 09/01/2013 Coursework Requirements: None July 2019 Intermediate Math Endorsement Page 2 Assignment Codes: Code Assignment Description 02001 Informal Mathematics 02002 General Math 02035 Math, Grade 5 02036 Math, Grade 6 02037 Math, Grade 7 02038 Math, Grade 8 02039 Grades 5-8 Math 02040 Grades 5-8 Pre-Algebra 02051 Pre-Algebra I 02052 Algebra I 02053 Algebra I - Part 1 02054 Algebra I - Part 2 02055 Transition Algebra 02056 Algebra II 02062 Integrated Mathematics