DOCSLIB.ORG

Technique for Estimating Magnitude and Frequency of Peak Flows in Maryland

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Technique for Estimating Magnitude and Frequency of Peak Flows in Maryland TECHNIQUEFORESTIMATINGMAGNITUDEAND FREQUENCYOFPEAKFLOWSINMARYLAND U.S.GEOLOGICALSURVEY Water-ResourcesInvestigationsReport95-4154 Preparedincooperationwiththe MARYLANDSTATEHIGHWAYADMINISTRATION CONVERSION FACTORS, VERTICAL DATUM, AND ABBREVIATIONS _____________________________________________________________________________________________________________________________________ Multiply By To obtain _____________________________________________________________________________________________________________________________________ foot (ft) 0.3048 meter mile (mi) 1.609 kilometer square mile (mi2) 2.590 square kilometer cubic foot per second (ft3/s) 0.02832 cubic meter per second cubic foot per second per square mile [(ft3/s)/mi2] 0.01093 cubic meter per second per square kilometer _____________________________________________________________________________________________________________________________________ Sea level: In this report, "sea level" refers to the National Geodetic Vertical Datum of 1929--a geodetic datum derived from a general adjustment of the first-order level nets of the United States and Canada, formerly called Sea Level Datum of 1929. TECHNIQUE FOR ESTIMATING MAGNITUDE AND FREQUENCY OF PEAK FLOWS IN MARYLAND By Jonathan J. A. Dillow _____________________________________________________________________________________________ U.S. GEOLOGICAL SURVEY Water-Resources Investigations Report 95-4154 Prepared in cooperation with the MARYLAND STATE HIGHWAY ADMINISTRATION Towson, Maryland 1996 U.S. DEPARTMENT OF THE INTERIOR BRUCE BABBITT, Secretary U.S. GEOLOGICAL SURVEY Gordon P. Eaton, Director _____________________________________________________________________________________________ For additional information write to: Copies of this report can be purchased from: U.S. Geological Survey District Chief Earth Science Information Center U.S. Geological Survey Open-File Reports Section 208 Carroll Building Box 25286, MS 517 8600 La Salle Road Denver Federal Center Towson, MD 21286 Denver, CO 80225 CONTENTS Abstract...............................................................................................................................................................1 Introduction ........................................................................................................................................................2 Background...........................................................................................................................................2 Purpose and scope.................................................................................................................................2 Description of study area ......................................................................................................................2 Physiographic setting ..............................................................................................................3 Geologic setting ......................................................................................................................4 Acknowledgments ................................................................................................................................5 Data collection and analysis ...............................................................................................................................5 Criteria for station selection..................................................................................................................5 Station flood-frequency analysis ..........................................................................................................8 Explanatory variable identification.......................................................................................................9 Methods for estimating magnitude and frequency of floods............................................................................12 Magnitude estimation method for ungaged streams...........................................................................13 Demonstration of the estimation method for ungaged streams.............................................13 Sensitivity analysis of explanatory variables ........................................................................13 Accuracy and limitations ......................................................................................................15 Magnitude estimation method for gaged streams...............................................................................16 Estimation method for a site at a gaged location ..................................................................16 Estimation method for a site near a gaged location ..............................................................19 Estimation method for a site between gaged locations.........................................................19 Summary and conclusions................................................................................................................................21 Selected references ...........................................................................................................................................22 Glossary ............................................................................................................................................................23 Appendix. .........................................................................................................................................................37 Analysis of the streamflow-gaging-station network...........................................................................38 FIGURES 0 1-3. Maps showing: 1. Study area and physiographic provinces in Maryland ...............................................................3 2. Location of streamflow-gaging stations and hydrologic study regions in Maryland and surrounding States. ........................................................................................6 3. Distribution of underlying limestone/dolomite in the Blue Ridge and Great Valley region in Maryland and surrounding States. .................................................11 04-04. Graph showing relation of observed to estimated 100-year peak discharges for the Appalachian Plateaus and Allegheny Ridges hydrologic region in Maryland and surrounding States........................................................................................................................16 Technique for estimating magnitude and frequency of peak flows in Maryland iii FIGURES--Continued 5a-5e. Graphs showing relation of maximum known unit discharge to drainage area for hydrologic regions: (a) Appalachian Plateaus and Allegheny Ridges, (b) Blue Ridge and Great Valley, (c) Piedmont, (d) Western Coastal Plain, and (e) Eastern Coastal Plain in Maryland and surrounding States...................................................17 05-06. Graph showing flood magnitudes and frequencies for the Potomac River. ......................................20 06-77. Map showing location of potential gaging station sites in Maryland................................................40 TABLES 01. Number of streamflow-gaging stations by hydrologic study region in Maryland and surrounding States ..................................................................................................8 02. Summary of drainage area, number of streamflow-gaging stations, and average years of record used in regression analyses for Maryland. .....................................................................8 03. Summary of statistics for variables associated with gaged basins in Maryland in regression analyses for hydrologic study regions in Maryland ...................................................10 04. Runoff-curve numbers defined by land use and hydrologic soil type................................................10 05. Standard errors of estimate and standards errors of prediction for estimation equations, by hydrologic study region in Maryland ....................................................................15 06. Equivalent years of record for estimation equations, by hydrologic study region in Maryland ..................................................................................................................................16 07. Basin characteristics and observed flood-frequency characteristics for selected drainage basins in Maryland and surrounding States ..................................................................24 8. Basin characteristics for potential gaging-station sites in Maryland. .................................................42 09. Maximum discharges at selected streamflow-gaging stations. ..........................................................43 iv Technique for estimating magnitude and frequency of peak flows in Maryland TECHNIQUE FOR ESTIMATING MAGNITUDE AND FREQUENCY OF PEAK FLOWS IN MARYLAND By Jonathan J.A. Dillow ABSTRACT A convenient and reliable technique for estimating flood magnitudes is required for effective flood-plain management and for the efficient design of bridges, culverts, embankments, and flood-protection structures. Methods are presented for estimating peak-flow magnitudes of selected frequencies, ranging from 2 to 500 years, for all nontidal drainage basins in Maryland. The methods were developed by generalized least-squares regression techniques using data from 219 gaged basins in and near Maryland. The State is divided into five hydrologic regions: the Appalachian
Load more

Recommended publications
  • NON-TIDAL BENTHIC MONITORING DATABASE: Version 3.5
    NON-TIDAL BENTHIC MONITORING DATABASE: Version 3.5 DATABASE DESIGN DOCUMENTATION AND DATA DICTIONARY 1 June 2013 Prepared for: United States Environmental Protection Agency Chesapeake Bay Program 410 Severn Avenue Annapolis, Maryland 21403 Prepared By: Interstate Commission on the Potomac River Basin 51 Monroe Street, PE-08 Rockville, Maryland 20850 Prepared for United States Environmental Protection Agency Chesapeake Bay Program 410 Severn Avenue Annapolis, MD 21403 By Jacqueline Johnson Interstate Commission on the Potomac River Basin To receive additional copies of the report please call or write: The Interstate Commission on the Potomac River Basin 51 Monroe Street, PE-08 Rockville, Maryland 20850 301-984-1908 Funds to support the document The Non-Tidal Benthic Monitoring Database: Version 3.0; Database Design Documentation And Data Dictionary was supported by the US Environmental Protection Agency Grant CB- CBxxxxxxxxxx-x Disclaimer The opinion expressed are those of the authors and should not be construed as representing the U.S. Government, the US Environmental Protection Agency, the several states or the signatories or Commissioners to the Interstate Commission on the Potomac River Basin: Maryland, Pennsylvania, Virginia, West Virginia or the District of Columbia. ii The Non-Tidal Benthic Monitoring Database: Version 3.5 TABLE OF CONTENTS BACKGROUND ................................................................................................................................................. 3 INTRODUCTION ..............................................................................................................................................
    [Show full text]
  • Jjjn'iwi'li Jmliipii Ill ^ANGLER
    JJJn'IWi'li jMlIipii ill ^ANGLER/ Ran a Looks A Bulltrog SEPTEMBER 1936 7 OFFICIAL STATE September, 1936 PUBLICATION ^ANGLER Vol.5 No. 9 C'^IP-^ '" . : - ==«rs> PUBLISHED MONTHLY COMMONWEALTH OF PENNSYLVANIA by the BOARD OF FISH COMMISSIONERS PENNSYLVANIA BOARD OF FISH COMMISSIONERS HI Five cents a copy — 50 cents a year OLIVER M. DEIBLER Commissioner of Fisheries C. R. BULLER 1 1 f Chief Fish Culturist, Bellefonte ALEX P. SWEIGART, Editor 111 South Office Bldg., Harrisburg, Pa. MEMBERS OF BOARD OLIVER M. DEIBLER, Chairman Greensburg iii MILTON L. PEEK Devon NOTE CHARLES A. FRENCH Subscriptions to the PENNSYLVANIA ANGLER Elwood City should be addressed to the Editor. Submit fee either HARRY E. WEBER by check or money order payable to the Common­ Philipsburg wealth of Pennsylvania. Stamps not acceptable. SAMUEL J. TRUSCOTT Individuals sending cash do so at their own risk. Dalton DAN R. SCHNABEL 111 Johnstown EDGAR W. NICHOLSON PENNSYLVANIA ANGLER welcomes contribu­ Philadelphia tions and photos of catches from its readers. Pro­ KENNETH A. REID per credit will be given to contributors. Connellsville All contributors returned if accompanied by first H. R. STACKHOUSE class postage. Secretary to Board =*KT> IMPORTANT—The Editor should be notified immediately of change in subscriber's address Please give both old and new addresses Permission to reprint will be granted provided proper credit notice is given Vol. 5 No. 9 SEPTEMBER, 1936 *ANGLER7 WHAT IS BEING DONE ABOUT STREAM POLLUTION By GROVER C. LADNER Deputy Attorney General and President, Pennsylvania Federation of Sportsmen PORTSMEN need not be told that stream pollution is a long uphill fight.
    [Show full text]
  • Road Log of the Geology of Frederick County, Virginia W
    Vol. 17 MAY, 1971 No. 2 ROAD LOG OF THE GEOLOGY OF FREDERICK COUNTY, VIRGINIA W. E. Nunan The following road log is a guide to geologic The user of this road log should keep in mind features along or near main roads in Frederick that automobile odometers vary in accuracy. Dis- County, Virginia. Distances and cumulative mile- tances between stops and road intersections ages between places where interesting and repre- should be checked frequently, especially at junc- sentative-lithologies, formational contacts, struc- tions or stream crossings immediately preceding tural features, fossils, and geomorphic features stops. The Frederick County road map of the occur are noted. At least one exposure for nearly Virginia Department of Highways, and the U. S. each formation is included in the log. Brief dis- Geological Survey 7.5-minute topographic maps cussions of the geological features observable at are recommended for use with this road log. the various stops is included in the text. Topographic maps covering Frederick County include Boyce, Capon Bridge, Capon Springs, A comprehensive report of the geology of the Glengary, Gore, Hayfield, Inwood, Middletown, Mountain Falls, Ridge, Stephens City, Stephen- County is presented in "Geology and Mineral Re- son, Wardensville, White Hall, and Winchester. sources of Frederick County" by Charles Butts The route of the road log (Figure 1) shows U. S. and R. S. Edmundson, Bulletin 80 of the Virginia and State Highways and those State Roads trav- Division of Mineral Resources. The publication eled or needed for reference at intersections. has a 1:62,500 scale geologic map in color, which Pertinent place names, streams, and railroad is available from the Division for $4.00 plus sales crossings are indicated.
    [Show full text]
  • Wills Creek Preassessment
    Wills Creek Preassessment Eric Null Len Lichvar Produced by Somerset Conservation District, 6024 Glades Pike Road Suite 103, Somerset, PA 1 2 Wills Creek Preassessment Eric Null Len Lichvar March 2010 Somerset Conservation District Funding for this project provided by the Foundation for Pennsylvania Watersheds With special assistance from the Pennsylvania Fish and Boat Commission Photos by Len Lichvar, Eric Null, and Amanda Deal Copies of this report may be obtained by contacting the Somerset Conservation District 6024 Glades Pike Road, Suite 103 Somerset, PA 15501 Phone (814) 445-4652 ext.5 Fax (814) 445-2044 E-mail [email protected] Report text may be accessed on the Somerset Conservation District Website http://www.somersetcd.org/ 3 Table of Contents Forward/Acknowledgements………...……………………………………………….7 Introduction………………………………………………………..………………….8 Methods………………………………………………………………………………10 Results…………………………………………………..…………………………....14 Discussion…………………………………………..………………………………..29 Recommendations …………………………………….…………………………….30 Literature Cited……………………………………….……………………………...31 Appendix 1— Macroinvertebrates collected at each site Appendix 2—Fishes collected at each site Wills Creek Sampling Station 5 4 List of Figures Figure 1. The Wills Creek watershed………………………………………………………....8 Figure 2. Wills Creek Preassessment sampling points…………………………………...….11 Figure 3. Macroinvertebrate species richness of the Wills Creek Watershed……………….15 Figure 4. Shannon-Weaver Diversity Index for the macroinvertebrates communities of the Wills Creek Watershed……………………………………………………..16 Figure 5. HBI scores for the Wills Creek watershed………………………………………....17 Figure 6. Percent EPT taxa in the Wills Creek watershed…………………………………....18 Figure 7. Percent Dominant taxa in the Wills Creek watershed……………………………...18 Figure 8. Percent acid tolerant taxa in the Wills Creek watershed…………………………...19 Figure 9. Fish species richness in the Wills Creek watershed ………………………………..21 Figure 10. Shannon-Weaver diversity index for fish communities in the Wills Creek Watershed…………………………………………………………………...22 Figure 11.
    [Show full text]
  • Adams County Conservation District
    Highlights of Conservation District Activities 2017 Presented by PACD Adams County Conservation District 2017 Feature Accomplishments Other Accomplishments Dirt, Gravel & Low Volume Road Maintenance Program Contact Information • Performed 265 E & S inspections with Resource Challenge 85% compliance Sediment is the largest pollutant by volume to the waters of the • Re-assessed 10 streams to upgrade Sherri Clayton-Williams Commonwealth of Pennsylvania. Unpaved roads not only Interim District Manager stream designation and protective uses. generate sediment, but also act as collectors for runoff and • Sponsored the Adams County sediment from adjacent land uses resulting in increased flood Envirothon programs involving 104 Charles Bennett flows in streams, and transport of sediment and other pollutant Board Chairman middle school students and 60 high into local waterways. school students • Installed 3 acres of riparian buffers Project Summary and Results 670 Old Harrisburg Road, Suite 201 through community volunteer projects. Technical assistance and funding to install driving surface Gettysburg, PA 17325 • Installed agricultural BMPs including 21 aggregate, new culverts, underdrains, ditching, and stormwater (717) 334-0636 waterways, 2 diversions and 3 terraces management to address problems on local roads that www.adamscounty.us • Provided technical assistance on EQIP adversely affect water quality. • Six project sites completed in 2017- $229,703.48 projects that brought an additional More Work to Do $232,767.00 into Adams County • Three
    [Show full text]
  • Brook Trout Outcome Management Strategy
    Brook Trout Outcome Management Strategy Introduction Brook Trout symbolize healthy waters because they rely on clean, cold stream habitat and are sensitive to rising stream temperatures, thereby serving as an aquatic version of a “canary in a coal mine”. Brook Trout are also highly prized by recreational anglers and have been designated as the state fish in many eastern states. They are an essential part of the headwater stream ecosystem, an important part of the upper watershed’s natural heritage and a valuable recreational resource. Land trusts in West Virginia, New York and Virginia have found that the possibility of restoring Brook Trout to local streams can act as a motivator for private landowners to take conservation actions, whether it is installing a fence that will exclude livestock from a waterway or putting their land under a conservation easement. The decline of Brook Trout serves as a warning about the health of local waterways and the lands draining to them. More than a century of declining Brook Trout populations has led to lost economic revenue and recreational fishing opportunities in the Bay’s headwaters. Chesapeake Bay Management Strategy: Brook Trout March 16, 2015 - DRAFT I. Goal, Outcome and Baseline This management strategy identifies approaches for achieving the following goal and outcome: Vital Habitats Goal: Restore, enhance and protect a network of land and water habitats to support fish and wildlife, and to afford other public benefits, including water quality, recreational uses and scenic value across the watershed. Brook Trout Outcome: Restore and sustain naturally reproducing Brook Trout populations in Chesapeake Bay headwater streams, with an eight percent increase in occupied habitat by 2025.
    [Show full text]
  • Occurrences of Laurel Run Fish Species
    LAUREL RUN Watershed Coldwater Conservation Plan August 2007 Prepared by Western Pennsylvania Conservancy Assistance provided by Somerset Conservation District Funded by a grant from The Coldwater Heritage Partnership TABLE of CONTENTS EXECUTIVE SUMMARY ............................................................................................................... 2 INTRODUCTION ........................................................................................................................ 3 Conservation Plan Objectives 3 Background 3 Geology and Topography 7 METHODS ................................................................................................................................. 10 Visual Assessment 10 Electrofishing 10 Macroinvertebrates 14 Water Chemistry 14 Public Participation 15 RESULTS .................................................................................................................................. 16 Visual Assessment 16 Electrofishing Results 17 Macroinvertebrate Results 22 Water Chemistry Results 27 Public Input 28 CONCLUSIONS .......................................................................................................................... 31 POSSIBLE FUNDING SOURCES ................................................................................................... 33 RECOMMENDATIONS ................................................................................................................. 34 WORKS CITED .........................................................................................................................
    [Show full text]
  • Wild Trout Waters (Natural Reproduction) - September 2021
    Pennsylvania Wild Trout Waters (Natural Reproduction) - September 2021 Length County of Mouth Water Trib To Wild Trout Limits Lower Limit Lat Lower Limit Lon (miles) Adams Birch Run Long Pine Run Reservoir Headwaters to Mouth 39.950279 -77.444443 3.82 Adams Hayes Run East Branch Antietam Creek Headwaters to Mouth 39.815808 -77.458243 2.18 Adams Hosack Run Conococheague Creek Headwaters to Mouth 39.914780 -77.467522 2.90 Adams Knob Run Birch Run Headwaters to Mouth 39.950970 -77.444183 1.82 Adams Latimore Creek Bermudian Creek Headwaters to Mouth 40.003613 -77.061386 7.00 Adams Little Marsh Creek Marsh Creek Headwaters dnst to T-315 39.842220 -77.372780 3.80 Adams Long Pine Run Conococheague Creek Headwaters to Long Pine Run Reservoir 39.942501 -77.455559 2.13 Adams Marsh Creek Out of State Headwaters dnst to SR0030 39.853802 -77.288300 11.12 Adams McDowells Run Carbaugh Run Headwaters to Mouth 39.876610 -77.448990 1.03 Adams Opossum Creek Conewago Creek Headwaters to Mouth 39.931667 -77.185555 12.10 Adams Stillhouse Run Conococheague Creek Headwaters to Mouth 39.915470 -77.467575 1.28 Adams Toms Creek Out of State Headwaters to Miney Branch 39.736532 -77.369041 8.95 Adams UNT to Little Marsh Creek (RM 4.86) Little Marsh Creek Headwaters to Orchard Road 39.876125 -77.384117 1.31 Allegheny Allegheny River Ohio River Headwater dnst to conf Reed Run 41.751389 -78.107498 21.80 Allegheny Kilbuck Run Ohio River Headwaters to UNT at RM 1.25 40.516388 -80.131668 5.17 Allegheny Little Sewickley Creek Ohio River Headwaters to Mouth 40.554253 -80.206802
    [Show full text]
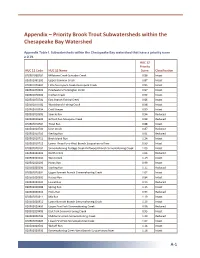
  • Appendix – Priority Brook Trout Subwatersheds Within the Chesapeake Bay Watershed
    Appendix – Priority Brook Trout Subwatersheds within the Chesapeake Bay Watershed Appendix Table I. Subwatersheds within the Chesapeake Bay watershed that have a priority score ≥ 0.79. HUC 12 Priority HUC 12 Code HUC 12 Name Score Classification 020501060202 Millstone Creek-Schrader Creek 0.86 Intact 020501061302 Upper Bowman Creek 0.87 Intact 020501070401 Little Nescopeck Creek-Nescopeck Creek 0.83 Intact 020501070501 Headwaters Huntington Creek 0.97 Intact 020501070502 Kitchen Creek 0.92 Intact 020501070701 East Branch Fishing Creek 0.86 Intact 020501070702 West Branch Fishing Creek 0.98 Intact 020502010504 Cold Stream 0.89 Intact 020502010505 Sixmile Run 0.94 Reduced 020502010602 Gifford Run-Mosquito Creek 0.88 Reduced 020502010702 Trout Run 0.88 Intact 020502010704 Deer Creek 0.87 Reduced 020502010710 Sterling Run 0.91 Reduced 020502010711 Birch Island Run 1.24 Intact 020502010712 Lower Three Runs-West Branch Susquehanna River 0.99 Intact 020502020102 Sinnemahoning Portage Creek-Driftwood Branch Sinnemahoning Creek 1.03 Intact 020502020203 North Creek 1.06 Reduced 020502020204 West Creek 1.19 Intact 020502020205 Hunts Run 0.99 Intact 020502020206 Sterling Run 1.15 Reduced 020502020301 Upper Bennett Branch Sinnemahoning Creek 1.07 Intact 020502020302 Kersey Run 0.84 Intact 020502020303 Laurel Run 0.93 Reduced 020502020306 Spring Run 1.13 Intact 020502020310 Hicks Run 0.94 Reduced 020502020311 Mix Run 1.19 Intact 020502020312 Lower Bennett Branch Sinnemahoning Creek 1.13 Intact 020502020403 Upper First Fork Sinnemahoning Creek 0.96
    [Show full text]
  • Estimating Mean Long-Term Hydrologic Budget Components For
    urren : C t R gy e o s l e o r a r d c Sanford et al., Hydrol Current Res 2015, 6:1 y h H Hydrology DOI: 10.4172/2157-7587.1000191 Current Research ISSN: 2157-7587 Research Article Open Access Estimating Mean Long-term Hydrologic Budget Components for Watersheds and Counties: An Application to the Commonwealth of Virginia, USA Ward E Sanford1*, David L Nelms2, Jason P Pope2 and David L Selnick3 1Mail Stop 431, U.S. Geological Survey, Reston, Virginia, 20171, USA 2U.S. Geological Survey, Richmond, Virginia, USA 3U.S. Geological Survey, Reston, Virginia, USA Abstract Mean long-term hydrologic budget components, such as recharge and base flow, are often difficult to estimate because they can vary substantially in space and time. Mean long-term fluxes were calculated in this study for precipitation, surface runoff, infiltration, total evapotranspiration (ET), riparian ET, recharge, base flow (or groundwater discharge) and net total outflow using long-term estimates of mean ET and precipitation and the assumption that the relative change in storage over that 30-year period is small compared to the total ET or precipitation. Fluxes of these components were first estimated on a number of real-time-gaged watersheds across Virginia. Specific conductance was used to distinguish and separate surface runoff from base flow. Specific-conductance (SC) data were collected every 15 minutes at 75 real-time gages for approximately 18 months between March 2007 and August 2008. Precipitation was estimated for 1971-2000 using PRISM climate data. Precipitation and temperature from the PRISM data were used to develop a regression-based relation to estimate total ET.
    [Show full text]
  • 2015 MS4 Permit Year 2 Annual Report
    GENERAL PERMIT FOR SMALL MUNICIPAL SEPARATE STORM SEWER SYSTEMS PERMIT NUMBER: VAR040053 Permit Year 2 Annual Report Reporting Period: July 1, 2014 - June 30, 2015 City of Winchester, Virginia Rouss City Hall Public Services Department 15 North Cameron Street Winchester, VA 22601 October 1, 2015 City of Winchester, Virginia Permit Year 2 Annual Report Table of Contents Section Page 1.0 Background Information ......................................................................................................... 1 2.0 Status of Permit Condition Compliance .................................................................................. 2 2.1. Assessment of BMP Appropriateness .................................................................................... 2 2.2. Required MS4 Program Plan Updates ................................................................................... 2 2.3. Measureable Goals Progress ................................................................................................. 3 3.0 Results of Collected Data ..................................................................................................... 18 4.0 Future Stormwater Activities ................................................................................................ 18 5.0 Changes in BMPs and Measurable Goals ............................................................................ 18 5.1. Changes in BMPs/Program Elements .................................................................................. 19 5.2. Changes in Measureable
    [Show full text]
  • GAME FISH STREAMS and RECORDS of FISHES from the POTOMAC-SHENANDOAH RIVER SYSTEM of VIRGINIA
    ) • GAME FISH STREAMS AND RECORDS OF FISHES FROM THE POTOMAC-SHENANDOAH RIVER SYSTEM Of VIRGINIA Robert D. Ross Associate Professor of Biology Technical Bulletin 140 April 1959 Virginia Agricultural Experiment Station Virginia Polytechnic Institute Blacksburg, Virginia ACKNOWLEDGMENTS The writer is grateful to Eugene S. Surber, Robert G. Martin and Jack M. Hoffman who directed the survey and gave their help and encouragement. A great deal of credit for the success of the Survey is due to all game wardens who rendered invaluable assistance. Special thanks are due to many sportsmen and assistant game wardens who helped the field crew. Personnel of the Commission of Game and Inland Fisheries, who helped in the work from time to time were William Fadley, William Hawley, Max Carpenter and Dixie L. Shumate. The Virginia Academy of Science gener- ously donated funds for the purchase of alcohol in which the fish collection was preserved. GAME FISH STREAMS AND RECORDS OF FISHES FROM THE SHENANDOAH-POTOMAC RIVER SYSTEMS OF VIRGINIA Robert D. Ross Associate Professor of Biology Virginia Polytechnic Institute INTRODUCTION From June 15 to September 15, 1956, the Commission of Game and Inland Fisheries, Division of Fisheries, Richmond, Virginia, undertook a survey of a major part of the Shenandoah-Potomac River watershed in Virginia. This work was done as Federal Aid Project No. F-8-R-3, in cooperation with Vir- ginia Cooperative Wildlife Research Unit, under the direction of Robert G. Martin, Dingell-Johnson Coordinator, and Jack M. Hoffman, Leader. Robert D. Ross, Crew Leader, and David W. Robinson and Charles H. Hanson worked in the field.
    [Show full text]