DOCSLIB.ORG

CHAPTER 8 Analytic Geometry 64

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
CHAPTER 8 Analytic Geometry 64 64 CHAPTER 8 Analytic Geometry 8.13. Find an equation for the perpendicular bisector of the line segment joining A(7,Ϫ8) and B(Ϫ2, 5). The perpendicular bisector of a segment consists of all points that are equidistant from its endpoints. Thus if PA ϭ PB, then P lies on the perpendicular bisector of AB. Let P have the unknown coordinates (x,y). Then, from the distance formula, PA ϭ PB if PA ϭ 2(x Ϫ 7)2 ϩ [y Ϫ (Ϫ8)]2 ϭ 2[x Ϫ (Ϫ2)]2 ϩ (y Ϫ 5)2 ϭ PB Squaring both sides and simplifying yields (x Ϫ 7)2 ϩ [y Ϫ (Ϫ8)]2 ϭ [x Ϫ (Ϫ2)]2 ϩ (y Ϫ 5)2 x2 Ϫ 14x ϩ 49 ϩ y2 ϩ 16y ϩ 64 ϭ x2 ϩ 4x ϩ 4 ϩ y2 Ϫ 10y ϩ 25 18x Ϫ 26y ϭ 84 9x Ϫ 13y ϭ 42 This is the equation satisfied by all points equidistant from A and B. Hence, it is the equation of the perpendicular bisector of AB. SUPPLEMENTARY PROBLEMS 8.14. Describe the set of points that satisfy the relations: (a) x ϭ 0; (b) x > 0; (c) xy < 0; (d) y > 1. Ans. (a) All points on the y-axis; (b) all points to the right of the y-axis; (c) all points in the second and fourth quadrants; (d) all points above the line y ϭ 1. 8.15. Find the distance between the following pairs of points: (a) (0,Ϫ7) and (7,0); (b) (Ϫ3 23,Ϫ3) and (3 23, 3), Ans. (a)7 22; (b) 12 8.16. Find the length and the midpoint of the line segment with the given endpoints: (a) A(1,8), B(Ϫ3,4); (b) A(3,Ϫ7), B(0,8); (c) A(1, 22), B(Ϫ1,5 22) 3 1 Ans.(a)length 4 22, midpoint (Ϫ1,6); (b)length 3 226, midpoint 2, 2 ; (c)length 6, midpoint (0,3 22) A B 8.17. Analyze the following for symmetry. Do not sketch graphs: (a) xy2 ϭ 4; (b) x3y ϭ 4; (c) ZxyZ ϭ 4; (d) x2 ϩ xy ϭ 4; (e) x2 ϩ y ϩ y2 ϭ 4; (f) x2 ϩ xy ϩ y2 ϭ 4 Ans. (a) x-axis symmetry; (b) origin symmetry; (c) x-axis, y-axis, origin symmetry; (d) origin symmetry; (e) y-axis symmetry; (f) origin symmetry 8.18. Analyze symmetry and intercepts, then sketch graphs of the following: (a) 3x ϩ 4y ϩ 12 ϭ 0(b)y2 ϭ 10 ϩ x (c) y2 Ϫ x2 ϭ 9(d) |y| Ϫ |x| ϭ 3 Ans. (a) Fig. 8-16: x-intercept Ϫ4, y-intercept Ϫ3, no symmetry Figure 8-16 CHAPTER 8 Analytic Geometry 65 (b) Fig. 8-17: x-intercept Ϫ10, y-intercepts Ϯ 210, x-axis symmetry Figure 8-17 (c) Fig. 8-18: no x-intercept, y-intercept Ϯ3, x-axis, y-axis, origin symmetry Figure 8-18 (d) Fig. 8-19: no x-intercept, y-intercepts Ϯ3, x-axis, y-axis, origin symmetry Figure 8-19 8.19. Analyze symmetry and intercepts, then sketch graphs of the following: y (a)x ϩ y ϭ 0 ; (b) y ϩ ZxZ ϭ 4; (c)x2 ϭ 4ZyZ ; 4 (d) ZyZ ϩ x2 ϭ 4; (e)ZxZ ϭ 4y2 ; (f) Ϫxy2 ϭ 4 2 Ans. (a) Fig. 8-20: x-intercepts 0, y-intercept 0, origin symmetry x –4 –2 2 4 –2 –4 Figure 8-20 66 CHAPTER 8 Analytic Geometry (b) Fig. 8-21: x-intercepts Ϯ4, y-intercept 4, y y-axis symmetry 4 3 2 1 x –6 –4 –2 2 4 6 –1 –2 Figure 8-21 (c) Fig. 8-22: x-intercept 0, y-intercept 0, x-axis, y y-axis, origin symmetry 2 1 x –6 –4 –2 2 4 6 –1 –2 Figure 8-22 (d) Fig. 8-23: x-intercepts Ϯ2, y-intercepts Ϯ4, x-axis, y y-axis, origin symmetry 15 10 5 x –6 –4 –2 2 4 6 –5 –10 –15 Figure 8-23 (e) Fig. 8-24: x-intercept 0, y-intercept 0, x-axis, y y-axis, origin symmetry 1.5 1 0.5 x –10 –5 5 10 –0.5 –1 –1.5 Figure 8-24 CHAPTER 8 Analytic Geometry 67 (f) Fig. 8-25: no intercepts, x-axis symmetry y 4 3 2 1 x –4 –3 –2 –1 1 2 3 4 –1 –2 –3 –4 Figure 8-25 1 5 4 8.20. Find the equations of the following circles: (a) center (5,Ϫ2), radius 210; (b) center 2,Ϫ2 , diameter 3; (c) center (3,8), passing through the origin; (d) center (Ϫ3,Ϫ4), tangent to the y-axis. A B 2 2 1 2 5 2 9 Ans. (a) (x Ϫ 5) ϩ (y ϩ 2) ϭ 210; (b) x Ϫ 2 ϩ y ϩ 2 ϭ 4; 2 2 2 2 (c) (x Ϫ 3) ϩ (y Ϫ 8) ϭ 73; (d) (x ϩA 3) ϩB (y ϩA 4) ϭB9 8.21. Find the equations of the following circles: (a) center (5,2), (3,Ϫ1) is a point on the circle; (b)(5,Ϫ5) and (Ϫ3,Ϫ9) are end points of a diameter. Ans.(a)(x Ϫ 5)2 ϩ (y Ϫ 2)2 ϭ 13; (b) (x Ϫ 1)2 ϩ (y ϩ 7)2 ϭ 20 8.22. For the following equations, determine whether they represent circles, and if so, find the center and radius: (a) x2 ϩ y2 ϩ 8x ϩ 2y ϭ 5; (b) x2 ϩ y2 Ϫ 4x Ϫ 8y ϩ 20 ϭ 0; (c) 2x2 ϩ 2y2 Ϫ 6x ϩ 14y ϭ 3; (d) x2 ϩ y2 ϩ 12x ϩ 20y ϩ 200 ϭ 0 Ans. (a) circle; center (Ϫ4, Ϫ1), radius 222; (b) this is not a circle; the graph consists only of the point (2,4); 3 7 (c) circle, center (2,Ϫ2), radius 4; (d) this is not a circle; there are no points on the graph. 8.23. Show that the triangle with vertices (Ϫ10,7), (Ϫ6,Ϫ2), and (3,2) is isosceles. 8.24. Show that the triangle with vertices (4, 23), (5,0), and (6, 23) is equilateral. 8.25. Show that the triangle with vertices , (1,1)(6,9) , and (9,Ϫ4) is an isosceles right triangle. 8.26. Show that the quadrilateral with vertices (Ϫ3,Ϫ3), (5,Ϫ1), (7,7), and (Ϫ1,5) is a rhombus. 8.27. Show that the quadrilateral with vertices (7,2), (10,0), (8,Ϫ3), and (5,Ϫ1) is a square. 8.28. (a) Find the equation of the perpendicular bisector of the line segment with endpoints (Ϫ2,Ϫ5) and (7,Ϫ1). (b) Show that the equation of the perpendicular bisector of the line segment with endpoints (x1,y1) and (x2,y2) x Ϫ x y Ϫ y can be written ϩ ϭ 0, where (x,y) are the coordinates of the midpoint of the segment. y2 Ϫ y1 x2 Ϫ x1 Ans. (a) 18x ϩ 8y ϭ 21.
Load more

Recommended publications
  • Analytic Geometry
    Guide Study Georgia End-Of-Course Tests Georgia ANALYTIC GEOMETRY TABLE OF CONTENTS INTRODUCTION ...........................................................................................................5 HOW TO USE THE STUDY GUIDE ................................................................................6 OVERVIEW OF THE EOCT .........................................................................................8 PREPARING FOR THE EOCT ......................................................................................9 Study Skills ........................................................................................................9 Time Management .....................................................................................10 Organization ...............................................................................................10 Active Participation ...................................................................................11 Test-Taking Strategies .....................................................................................11 Suggested Strategies to Prepare for the EOCT ..........................................12 Suggested Strategies the Day before the EOCT ........................................13 Suggested Strategies the Morning of the EOCT ........................................13 Top 10 Suggested Strategies during the EOCT .........................................14 TEST CONTENT ........................................................................................................15
    [Show full text]
  • Chapter 11. Three Dimensional Analytic Geometry and Vectors
    Chapter 11. Three dimensional analytic geometry and vectors. Section 11.5 Quadric surfaces. Curves in R2 : x2 y2 ellipse + =1 a2 b2 x2 y2 hyperbola − =1 a2 b2 parabola y = ax2 or x = by2 A quadric surface is the graph of a second degree equation in three variables. The most general such equation is Ax2 + By2 + Cz2 + Dxy + Exz + F yz + Gx + Hy + Iz + J =0, where A, B, C, ..., J are constants. By translation and rotation the equation can be brought into one of two standard forms Ax2 + By2 + Cz2 + J =0 or Ax2 + By2 + Iz =0 In order to sketch the graph of a quadric surface, it is useful to determine the curves of intersection of the surface with planes parallel to the coordinate planes. These curves are called traces of the surface. Ellipsoids The quadric surface with equation x2 y2 z2 + + =1 a2 b2 c2 is called an ellipsoid because all of its traces are ellipses. 2 1 x y 3 2 1 z ±1 ±2 ±3 ±1 ±2 The six intercepts of the ellipsoid are (±a, 0, 0), (0, ±b, 0), and (0, 0, ±c) and the ellipsoid lies in the box |x| ≤ a, |y| ≤ b, |z| ≤ c Since the ellipsoid involves only even powers of x, y, and z, the ellipsoid is symmetric with respect to each coordinate plane. Example 1. Find the traces of the surface 4x2 +9y2 + 36z2 = 36 1 in the planes x = k, y = k, and z = k. Identify the surface and sketch it. Hyperboloids Hyperboloid of one sheet. The quadric surface with equations x2 y2 z2 1.
    [Show full text]
  • Lesson 3: Rectangles Inscribed in Circles
    NYS COMMON CORE MATHEMATICS CURRICULUM Lesson 3 M5 GEOMETRY Lesson 3: Rectangles Inscribed in Circles Student Outcomes . Inscribe a rectangle in a circle. Understand the symmetries of inscribed rectangles across a diameter. Lesson Notes Have students use a compass and straightedge to locate the center of the circle provided. If necessary, remind students of their work in Module 1 on constructing a perpendicular to a segment and of their work in Lesson 1 in this module on Thales’ theorem. Standards addressed with this lesson are G-C.A.2 and G-C.A.3. Students should be made aware that figures are not drawn to scale. Classwork Scaffolding: Opening Exercise (9 minutes) Display steps to construct a perpendicular line at a point. Students follow the steps provided and use a compass and straightedge to find the center of a circle. This exercise reminds students about constructions previously . Draw a segment through the studied that are needed in this lesson and later in this module. point, and, using a compass, mark a point equidistant on Opening Exercise each side of the point. Using only a compass and straightedge, find the location of the center of the circle below. Label the endpoints of the Follow the steps provided. segment 퐴 and 퐵. Draw chord 푨푩̅̅̅̅. Draw circle 퐴 with center 퐴 . Construct a chord perpendicular to 푨푩̅̅̅̅ at and radius ̅퐴퐵̅̅̅. endpoint 푩. Draw circle 퐵 with center 퐵 . Mark the point of intersection of the perpendicular chord and the circle as point and radius ̅퐵퐴̅̅̅. 푪. Label the points of intersection .
    [Show full text]
  • Squaring the Circle a Case Study in the History of Mathematics the Problem
    Squaring the Circle A Case Study in the History of Mathematics The Problem Using only a compass and straightedge, construct for any given circle, a square with the same area as the circle. The general problem of constructing a square with the same area as a given figure is known as the Quadrature of that figure. So, we seek a quadrature of the circle. The Answer It has been known since 1822 that the quadrature of a circle with straightedge and compass is impossible. Notes: First of all we are not saying that a square of equal area does not exist. If the circle has area A, then a square with side √A clearly has the same area. Secondly, we are not saying that a quadrature of a circle is impossible, since it is possible, but not under the restriction of using only a straightedge and compass. Precursors It has been written, in many places, that the quadrature problem appears in one of the earliest extant mathematical sources, the Rhind Papyrus (~ 1650 B.C.). This is not really an accurate statement. If one means by the “quadrature of the circle” simply a quadrature by any means, then one is just asking for the determination of the area of a circle. This problem does appear in the Rhind Papyrus, but I consider it as just a precursor to the construction problem we are examining. The Rhind Papyrus The papyrus was found in Thebes (Luxor) in the ruins of a small building near the Ramesseum.1 It was purchased in 1858 in Egypt by the Scottish Egyptologist A.
    [Show full text]
  • ANALYTIC GEOMETRY Revision Log
    Guide Study Georgia End-Of-Course Tests Georgia ANALYTIC GEOMETRYJanuary 2014 Revision Log August 2013: Unit 7 (Applications of Probability) page 200; Key Idea #7 – text and equation were updated to denote intersection rather than union page 203; Review Example #2 Solution – union symbol has been corrected to intersection symbol in lines 3 and 4 of the solution text January 2014: Unit 1 (Similarity, Congruence, and Proofs) page 33; Review Example #2 – “Segment Addition Property” has been updated to “Segment Addition Postulate” in step 13 of the solution page 46; Practice Item #2 – text has been specified to indicate that point V lies on segment SU page 59; Practice Item #1 – art has been updated to show points on YX and YZ Unit 3 (Circles and Volume) page 74; Key Idea #17 – the reference to Key Idea #15 has been updated to Key Idea #16 page 84; Key Idea #3 – the degree symbol (°) has been removed from 360, and central angle is noted by θ instead of x in the formula and the graphic page 84; Important Tip – the word “formulas” has been corrected to “formula”, and x has been replaced by θ in the formula for arc length page 85; Key Idea #4 – the degree symbol (°) has been added to the conversion factor page 85; Key Idea #5 – text has been specified to indicate a central angle, and central angle is noted by θ instead of x page 85; Key Idea #6 – the degree symbol (°) has been removed from 360, and central angle is noted by θ instead of x in the formula and the graphic page 87; Solution Step i – the degree symbol (°) has been added to the conversion
    [Show full text]
  • Analytic Geometry
    STATISTIC ANALYTIC GEOMETRY SESSION 3 STATISTIC SESSION 3 Session 3 Analytic Geometry Geometry is all about shapes and their properties. If you like playing with objects, or like drawing, then geometry is for you! Geometry can be divided into: Plane Geometry is about flat shapes like lines, circles and triangles ... shapes that can be drawn on a piece of paper Solid Geometry is about three dimensional objects like cubes, prisms, cylinders and spheres Point, Line, Plane and Solid A Point has no dimensions, only position A Line is one-dimensional A Plane is two dimensional (2D) A Solid is three-dimensional (3D) Plane Geometry Plane Geometry is all about shapes on a flat surface (like on an endless piece of paper). 2D Shapes Activity: Sorting Shapes Triangles Right Angled Triangles Interactive Triangles Quadrilaterals (Rhombus, Parallelogram, etc) Rectangle, Rhombus, Square, Parallelogram, Trapezoid and Kite Interactive Quadrilaterals Shapes Freeplay Perimeter Area Area of Plane Shapes Area Calculation Tool Area of Polygon by Drawing Activity: Garden Area General Drawing Tool Polygons A Polygon is a 2-dimensional shape made of straight lines. Triangles and Rectangles are polygons. Here are some more: Pentagon Pentagra m Hexagon Properties of Regular Polygons Diagonals of Polygons Interactive Polygons The Circle Circle Pi Circle Sector and Segment Circle Area by Sectors Annulus Activity: Dropping a Coin onto a Grid Circle Theorems (Advanced Topic) Symbols There are many special symbols used in Geometry. Here is a short reference for you:
    [Show full text]
  • Topics in Complex Analytic Geometry
    version: February 24, 2012 (revised and corrected) Topics in Complex Analytic Geometry by Janusz Adamus Lecture Notes PART II Department of Mathematics The University of Western Ontario c Copyright by Janusz Adamus (2007-2012) 2 Janusz Adamus Contents 1 Analytic tensor product and fibre product of analytic spaces 5 2 Rank and fibre dimension of analytic mappings 8 3 Vertical components and effective openness criterion 17 4 Flatness in complex analytic geometry 24 5 Auslander-type effective flatness criterion 31 This document was typeset using AMS-LATEX. Topics in Complex Analytic Geometry - Math 9607/9608 3 References [I] J. Adamus, Complex analytic geometry, Lecture notes Part I (2008). [A1] J. Adamus, Natural bound in Kwieci´nski'scriterion for flatness, Proc. Amer. Math. Soc. 130, No.11 (2002), 3165{3170. [A2] J. Adamus, Vertical components in fibre powers of analytic spaces, J. Algebra 272 (2004), no. 1, 394{403. [A3] J. Adamus, Vertical components and flatness of Nash mappings, J. Pure Appl. Algebra 193 (2004), 1{9. [A4] J. Adamus, Flatness testing and torsion freeness of analytic tensor powers, J. Algebra 289 (2005), no. 1, 148{160. [ABM1] J. Adamus, E. Bierstone, P. D. Milman, Uniform linear bound in Chevalley's lemma, Canad. J. Math. 60 (2008), no.4, 721{733. [ABM2] J. Adamus, E. Bierstone, P. D. Milman, Geometric Auslander criterion for flatness, to appear in Amer. J. Math. [ABM3] J. Adamus, E. Bierstone, P. D. Milman, Geometric Auslander criterion for openness of an algebraic morphism, preprint (arXiv:1006.1872v1). [Au] M. Auslander, Modules over unramified regular local rings, Illinois J.
    [Show full text]
  • Geometry Course Outline
    GEOMETRY COURSE OUTLINE Content Area Formative Assessment # of Lessons Days G0 INTRO AND CONSTRUCTION 12 G-CO Congruence 12, 13 G1 BASIC DEFINITIONS AND RIGID MOTION Representing and 20 G-CO Congruence 1, 2, 3, 4, 5, 6, 7, 8 Combining Transformations Analyzing Congruency Proofs G2 GEOMETRIC RELATIONSHIPS AND PROPERTIES Evaluating Statements 15 G-CO Congruence 9, 10, 11 About Length and Area G-C Circles 3 Inscribing and Circumscribing Right Triangles G3 SIMILARITY Geometry Problems: 20 G-SRT Similarity, Right Triangles, and Trigonometry 1, 2, 3, Circles and Triangles 4, 5 Proofs of the Pythagorean Theorem M1 GEOMETRIC MODELING 1 Solving Geometry 7 G-MG Modeling with Geometry 1, 2, 3 Problems: Floodlights G4 COORDINATE GEOMETRY Finding Equations of 15 G-GPE Expressing Geometric Properties with Equations 4, 5, Parallel and 6, 7 Perpendicular Lines G5 CIRCLES AND CONICS Equations of Circles 1 15 G-C Circles 1, 2, 5 Equations of Circles 2 G-GPE Expressing Geometric Properties with Equations 1, 2 Sectors of Circles G6 GEOMETRIC MEASUREMENTS AND DIMENSIONS Evaluating Statements 15 G-GMD 1, 3, 4 About Enlargements (2D & 3D) 2D Representations of 3D Objects G7 TRIONOMETRIC RATIOS Calculating Volumes of 15 G-SRT Similarity, Right Triangles, and Trigonometry 6, 7, 8 Compound Objects M2 GEOMETRIC MODELING 2 Modeling: Rolling Cups 10 G-MG Modeling with Geometry 1, 2, 3 TOTAL: 144 HIGH SCHOOL OVERVIEW Algebra 1 Geometry Algebra 2 A0 Introduction G0 Introduction and A0 Introduction Construction A1 Modeling With Functions G1 Basic Definitions and Rigid
    [Show full text]
  • Chapter 1: Analytic Geometry
    1 Analytic Geometry Much of the mathematics in this chapter will be review for you. However, the examples will be oriented toward applications and so will take some thought. In the (x,y) coordinate system we normally write the x-axis horizontally, with positive numbers to the right of the origin, and the y-axis vertically, with positive numbers above the origin. That is, unless stated otherwise, we take “rightward” to be the positive x- direction and “upward” to be the positive y-direction. In a purely mathematical situation, we normally choose the same scale for the x- and y-axes. For example, the line joining the origin to the point (a,a) makes an angle of 45◦ with the x-axis (and also with the y-axis). In applications, often letters other than x and y are used, and often different scales are chosen in the horizontal and vertical directions. For example, suppose you drop something from a window, and you want to study how its height above the ground changes from second to second. It is natural to let the letter t denote the time (the number of seconds since the object was released) and to let the letter h denote the height. For each t (say, at one-second intervals) you have a corresponding height h. This information can be tabulated, and then plotted on the (t, h) coordinate plane, as shown in figure 1.0.1. We use the word “quadrant” for each of the four regions into which the plane is divided by the axes: the first quadrant is where points have both coordinates positive, or the “northeast” portion of the plot, and the second, third, and fourth quadrants are counted off counterclockwise, so the second quadrant is the northwest, the third is the southwest, and the fourth is the southeast.
    [Show full text]
  • Find the Radius Or Diameter of the Circle with the Given Dimensions. 2
    8-1 Circumference Find the radius or diameter of the circle with the given dimensions. 2. d = 24 ft SOLUTION: The radius is 12 feet. ANSWER: 12 ft Find the circumference of the circle. Use 3.14 or for π. Round to the nearest tenth if necessary. 4. SOLUTION: The circumference of the circle is about 25.1 feet. ANSWER: 3.14 × 8 = 25.1 ft eSolutions Manual - Powered by Cognero Page 1 8-1 Circumference 6. SOLUTION: The circumference of the circle is about 22 miles. ANSWER: 8. The Belknap shield volcano is located in the Cascade Range in Oregon. The volcano is circular and has a diameter of 5 miles. What is the circumference of this volcano to the nearest tenth? SOLUTION: The circumference of the volcano is about 15.7 miles. ANSWER: 15.7 mi eSolutions Manual - Powered by Cognero Page 2 8-1 Circumference Copy and Solve Show your work on a separate piece of paper. Find the diameter given the circumference of the object. Use 3.14 for π. 10. a satellite dish with a circumference of 957.7 meters SOLUTION: The diameter of the satellite dish is 305 meters. ANSWER: 305 m 12. a nickel with a circumference of about 65.94 millimeters SOLUTION: The diameter of the nickel is 21 millimeters. ANSWER: 21 mm eSolutions Manual - Powered by Cognero Page 3 8-1 Circumference Find the distance around the figure. Use 3.14 for π. 14. SOLUTION: The distance around the figure is 5 + 5 or 10 feet plus of the circumference of a circle with a radius of 5 feet.
    [Show full text]
  • Hyperbolic Geometry
    Flavors of Geometry MSRI Publications Volume 31,1997 Hyperbolic Geometry JAMES W. CANNON, WILLIAM J. FLOYD, RICHARD KENYON, AND WALTER R. PARRY Contents 1. Introduction 59 2. The Origins of Hyperbolic Geometry 60 3. Why Call it Hyperbolic Geometry? 63 4. Understanding the One-Dimensional Case 65 5. Generalizing to Higher Dimensions 67 6. Rudiments of Riemannian Geometry 68 7. Five Models of Hyperbolic Space 69 8. Stereographic Projection 72 9. Geodesics 77 10. Isometries and Distances in the Hyperboloid Model 80 11. The Space at Infinity 84 12. The Geometric Classification of Isometries 84 13. Curious Facts about Hyperbolic Space 86 14. The Sixth Model 95 15. Why Study Hyperbolic Geometry? 98 16. When Does a Manifold Have a Hyperbolic Structure? 103 17. How to Get Analytic Coordinates at Infinity? 106 References 108 Index 110 1. Introduction Hyperbolic geometry was created in the first half of the nineteenth century in the midst of attempts to understand Euclid’s axiomatic basis for geometry. It is one type of non-Euclidean geometry, that is, a geometry that discards one of Euclid’s axioms. Einstein and Minkowski found in non-Euclidean geometry a This work was supported in part by The Geometry Center, University of Minnesota, an STC funded by NSF, DOE, and Minnesota Technology, Inc., by the Mathematical Sciences Research Institute, and by NSF research grants. 59 60 J. W. CANNON, W. J. FLOYD, R. KENYON, AND W. R. PARRY geometric basis for the understanding of physical time and space. In the early part of the twentieth century every serious student of mathematics and physics studied non-Euclidean geometry.
    [Show full text]
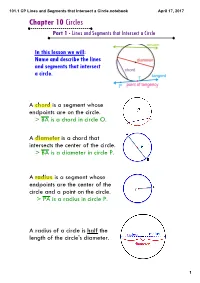
  • 101.1 CP Lines and Segments That Intersect a Circle.Notebook April 17, 2017 Chapter 10 Circles Part 1 - Lines and Segments That Intersect a Circle
    101.1 CP Lines and Segments that Intersect a Circle.notebook April 17, 2017 Chapter 10 Circles Part 1 - Lines and Segments that Intersect a Circle In this lesson we will: Name and describe the lines and segments that intersect a circle. A chord is a segment whose endpoints are on the circle. > BA is a chord in circle O. A diameter is a chord that intersects the center of the circle. > BA is a diameter in circle P. A radius is a segment whose endpoints are the center of the circle and a point on the circle. > PA is a radius in circle P. A radius of a circle is half the length of the circle's diameter. 1 101.1 CP Lines and Segments that Intersect a Circle.notebook April 17, 2017 A tangent is a line or segment that intersects a circle at one point. The point of tangency is the point where the line or segment intersects the circle > line t is a tangent line to circle O and P is the point of tangency A common tangent is a line that is tangent to two circles. A secant is a line that intersects a circle at two points. The segment part of a secant contained inside the circle is a chord. > line AB is a secant in circle O > segment AB is a chord in circle O 2 101.1 CP Lines and Segments that Intersect a Circle.notebook April 17, 2017 Examples: Naming Lines and Segments that Intersect Circles Name each line or segment that intersects 8L.
    [Show full text]