DOCSLIB.ORG

Corequisite Mathematics Education at Missouri Community

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Corequisite Mathematics Education at Missouri Community COREQUISITE MATHEMATICS EDUCATION AT MISSOURI COMMUNITY COLLEGES ________________________________________________________________________ A Dissertation presented to the Faculty of the Graduate School at the University of Missouri-Columbia ________________________________________________________________________ In Partial Fulfillment of the Requirements for the Degree Doctor of Education ________________________________________________________________________ By TRISHA WHITE Dr. Cynthia MacGregor, Dissertation Supervisor DECEMBER 2020 © Copyright by Trisha White 2020 All Rights Reserved The undersigned, appointed by the dean of the Graduate School, have examined the Dissertation entitled COREQUISITE MATHEMATICS EDUCATION AT MISSOURI COMMUNITY COLLEGES presented by Trisha White, a candidate for the degree of Doctorate of Educational Leadership and Policy Analysis, and hereby certify that, in their opinion, it is worthy of acceptance. ______________________________________________________________ Dr. Cynthia MacGregor, Chair ______________________________________________________________ Dr. Ximena Uribe-Zarain ______________________________________________________________ Dr. Tracey Glaessgen ______________________________________________________________ Dr. William Agnew DEDICATION This dissertation is dedicated to my precious family, friends, and colleagues who have encouraged and supported me throughout my doctoral work. If I have learned anything, it is that we truly need each other. ACKNOWLEDGEMENTS I would like to thank my dissertation supervisor, Dr. Cynthia MacGregor, who provided expertise and support. She kept me on track and pushed me to jump into intimidating tasks. I would also like to thank Dr. Ximena Uribe-Zarain who helped me learn to manage a massive data set and provided statistical expertise. In addition, I would like to thank the other members of my dissertation committee, Dr. Tracey Glaessgen and Dr. William Agnew. Thank you for the time spent reading and responding to my writing. I am grateful for your knowledge and support. Finally, I would like to thank my friend and fellow math teacher, Rima Freeman. She reminded me to celebrate the small victories and listened with interest (for months and months) to my thoughts and troubles surrounding my research. Thank you for your friendship. ii TABLE OF CONTENTS ACKNOWLEDGEMENTS ................................................................................................ ii LIST OF FIGURES .......................................................................................................... ix LIST OF TABLES ...............................................................................................................x ABSTRACT ....................................................................................................................... xi Contents SECTION ONE: INTRODUCTION TO THE DISSERTATION ..................................... 1 Background of the Study ................................................................................................ 2 Statement of the Problem ................................................................................................ 3 Purpose ............................................................................................................................ 4 Research Questions ......................................................................................................... 5 Theoretical Framework ................................................................................................... 6 Design of the Study ......................................................................................................... 8 Setting ......................................................................................................................... 8 Participants ................................................................................................................ 10 Role of the Researcher .............................................................................................. 11 Data Collection Tools ............................................................................................... 11 Data Analysis ............................................................................................................ 13 Integration of the Qualitative and Quantitative Data ................................................ 16 Limitations .................................................................................................................... 16 iii Definitions of Key Terminology ................................................................................... 17 Significance of the Study .............................................................................................. 19 Summary ....................................................................................................................... 20 SECTION TWO: PRACTITIONER SETTING OF STUDY .......................................... 21 Community Colleges in Missouri ................................................................................. 22 Local Context of Community Colleges in Missouri ................................................. 22 Comparisons of Missouri Community Colleges ....................................................... 26 History and Background of Policies Influencing Missouri Public Institutions ............ 28 Organizational Analysis ................................................................................................ 31 The Structural Frame ................................................................................................ 31 The Political Frame ................................................................................................... 33 Leadership Analysis ...................................................................................................... 36 Implications for Research in the Practitioner Setting ................................................... 37 Summary ....................................................................................................................... 38 SECTION THREE: SCHOLARLY REVIEW FOR THE STUDY ................................. 39 Theories of Retention and Persistence .......................................................................... 42 Social and Cultural Reproduction ............................................................................. 42 Tinto’s Theory of Student Retention ........................................................................ 43 Academic Momentum ............................................................................................... 46 Summary of Theories of Retention and Persistence ................................................. 50 iv Effectiveness of Developmental Education of College Completion ............................ 50 Alternatives to Traditional Developmental Education Approaches ............................. 55 Emporium Model ...................................................................................................... 55 Corequisite Remediation ........................................................................................... 56 Technology Use in Developmental Education ......................................................... 58 Summary ................................................................................................................... 59 Issues Driving Developmental Education Reform ....................................................... 59 Conclusion .................................................................................................................... 62 SECTION FOUR: CONTRIBUTION TO PRACTICE ................................................... 63 EXECUTIVE SUMMARY Transforming Mathematics Education at Missouri Community Colleges .................................................................................................... 65 Power Point Presentation .............................................................................................. 67 Appendix A ................................................................................................................... 77 Crowder College ....................................................................................................... 77 East Central College ................................................................................................. 79 Jefferson College ...................................................................................................... 81 Metropolitan Community College ............................................................................ 83 Mineral Area College ................................................................................................ 85 Moberly Area Community College .......................................................................... 87 North Central Missouri College ................................................................................ 89 v Ozarks Technical Community College ..................................................................... 91 Saint Charles Community College............................................................................ 93 Saint Louis Community College ............................................................................... 95 State Fair Community College.................................................................................. 97 Three Rivers College ...............................................................................................
Load more

Recommended publications
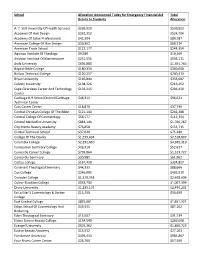
  • School Allocation Announced Today for Emergency Financial Aid Grants to Students Total Allocation A. T. Still University of Heal
    School Allocation Announced Today for Emergency Financial Aid Total Grants to Students Allocation A. T. Still University Of Health Sciences $269,910 $539,820 Academy Of Hair Design $262,352 $524,704 Academy Of Salon Professionals $42,394 $84,787 American College Of Hair Design $29,362 $58,724 American Trade School $122,177 $244,354 Aquinas Institute Of Theology $9,580 $19,160 Aviation Institute Of Maintenance $251,556 $503,111 Avila University $695,880 $1,391,760 Baptist Bible College $180,334 $360,668 Bolivar Technical College $120,237 $240,473 Bryan University $166,844 $333,687 Calvary University $108,226 $216,452 Cape Girardeau Career And Technology $103,215 $206,430 Center Carthage R-9 School District/Carthage $48,311 $96,621 Technical Center Cass Career Center $18,870 $37,739 Central Christian College Of The Bible $121,144 $242,288 Central College Of Cosmetology $56,177 $112,354 Central Methodist University $883,144 $1,766,287 City Pointe Beauty Academy $76,858 $153,715 Clinton Technical School $37,640 $75,280 College Of The Ozarks $1,259,404 $2,518,807 Columbia College $2,192,660 $4,385,319 Conception Seminary College $26,314 $52,627 Concorde Career College $759,864 $1,519,727 Concordia Seminary $30,981 $61,962 Cottey College $167,429 $334,857 Covenant Theological Seminary $44,333 $88,666 Cox College $246,005 $492,010 Crowder College $1,319,348 $2,638,696 Culver-Stockton College $533,700 $1,067,399 Drury University $1,235,101 $2,470,201 Ea La Mar'S Cosmetology & Barber $15,250 $30,499 College East Central College $825,661 $1,651,321
    [Show full text]
  • Medical Laboratory Technician Degree Plan
    Revised Core 8/10/2020 lmj Effective Fall 2020 Mineral Area College Associate of Applied Science MEDICAL LABORATORY TECHNICIAN (Major Code: MT-AP) CIP 51.1004 Student Name: __________________________________________ ID#: _______________________ The NAACLS Accredited Missouri Health Professions Consortium (MHPC) MLT Program curriculum includes virtual classroom instruction, on-campus laboratory instruction, and an off-campus clinical rotation component encompassing the areas of Hematology and Coagulation, Clinical Microbiology, Parasitology, Mycology and Virology, Immunohematology, Clinical Chemistry and Urinalysis, Immunology and Phlebotomy. The classroom lecture component is taught by MACC faculty and is recorded for the MLT students located at East Central College, Mineral Area College, MACC, North Central Missouri College, Three Rivers College, and State Fair Community College campuses using online learning management system technology. In addition, all MLT students will be required to travel to the MACC Mexico Campus at designated times during the fall and spring semesters to participate in “centralized lab” sessions that bring the students from all campuses together for group lab activities and testing. Any required lodging will be at the student’s expense. Pre-Professional Coursework Spring: Professional Coursework BIO2600 Human Anatomy..…….……….…..….5 _____ _____ MLT2700 Immunohematology……………5 _____ BIO2620 Human Physiology..….……….…..…..5 _____ _____ MLT2800 Clinical Microbiology.………...4 _____ HIS1230 American History I OR _____
    [Show full text]
  • Mineral Area College 2010-12 Catalog Please Note
    MINERAL AREA COLLEGE 2010-12 CATALOG PLEASE NOTE ACT and COMPASS placement scores changed April 4, 2011 for the following courses: ENG0960 – Basic Writing Skills I Learning Center Modules ENG0210, 0220, 0230 ENG0970 – Basic Writing Skills II Learning Center Modules ENG0240, 0250, 0260 Learning Center Modules ENG0010, 0020 Reading Improvement/Vocabulary Improvement ENG0990 – Reading & Study Skills Learning Center Modules ENG0070, 0080, 0090 ENG1330 – English Composition I MAT0900 – Arithmetic Learning Center Modules MAT0020, 0030, 0040 MAT0950 – Elementary Algebra Learning Center Modules MAT0110, 0120, 0130 MAT1130 – Intermediate Algebra MAT1230 - College Algebra MAT1330 - Trigonometry MAT1530 – Foundations of Math MAT1600 – Calculus for Business and the Social Sciences MAT1650 – Analytical Geometry & Calculus I TEC1900 – Technical Mathematics I Please see Addendum on the last page of the catalog for specific placement score information. 2010-2012 Mineral Area College Catalog — Table of Contents — Telephone Numbers............2 Student Consumer Rights Business Management .............. 68 Information ............................... 32 Business Management Greetings .............................3 —Accounting ........................... 68 Trustees ...............................4 Student Activities..............33 Business Management Student Organizations ............... 33 Academic Calendar.............5 —Microcomputers.................... 69 Departmental Activities .............. 35 Computer Networking ................ 69 About Mineral
    [Show full text]
  • School Deadline Washington University of St
    Priority FAFSA School Deadline Washington University of St. Louis 1-Feb College of the Ozarks 15-Feb Westminster College 15-Feb Columbia College 1-Mar Cottey College 1-Mar Culver-Stockton College 1-Mar East Central College 1-Mar Evangel University 1-Mar Missouri University of Science and Technology 1-Mar Missouri Western State University 1-Mar Rockhurst University 1-Mar Saint Louis University 1-Mar Southeast Missouri State University 1-Mar Stephens College 1-Mar University of Central Missouri 1-Mar University of Missouri 1-Mar University of Missouri- Kansas City 1-Mar University of Missouri- St. Louis 1-Mar Webster University 1-Mar To be sure, call the Student Financial Services (SFS) Office at 573-592-1793 to confirm your deadline for processing. William Woods University 1-Mar William Jewell College 10-Mar Drury University 15-Mar Lindenwood University 15-Mar Park University 15-Mar Southwest Baptist University 15-Mar Missouri State University - West Plains 31-Mar St. Louis College of Pharmacy 31-Mar Avila University 1-Apr Baptist Bible College 1-Apr Calvary Bible College 1-Apr Central Bible College 1-Apr Central Christian College of the Bible 1-Apr Crowder College 1-Apr Fontbonne University 1-Apr Gateway College of Evangelism 1-Apr Hannibal-LaGrange College 1-Apr Harris-Stowe State University 1-Apr Jefferson College 1-Apr Lincoln University 1-Apr Logan College of Chiropractic 1-Apr Maryville University 1-Apr Messenger College 1-Apr Metropolitan Community College 1-Apr Mineral Area College 1-Apr Missouri Baptist University 1-Apr Missouri Southern State University 1-Apr Missouri State University 1-Apr Missouri Valley College 1-Apr Moberly Area Community College 1-Apr North Central Missouri College 1-Apr Northwest Missouri State University 1-Apr Ozark Christian College 1-Apr Ozarks Technical Community College 1-Apr Ranken Technical College 1-Apr Rolla Technical Institute/Center 1-Apr Saint Louis Christian College 1-Apr St.
    [Show full text]
  • Missouri College Transfer Guide 2016-2017 Missouri College Transfer Guide
    Missouri College Transfer Guide 2016-2017 Missouri College Transfer Guide For many different reasons, community college students choose to transfer to a university to complete a bachelor’s degree. Choosing to start your education by completing a degree at a community college is a smart choice for several different reasons which include: Ability to stay at home (or closer to home) Save money – tuition and fees at a community college are much less than those at a four-year university General education requirements – You have the time to consider where you would like to transfer (and possibly major in) while completing general education courses at a community college Smaller class sizes (compared to a university) As you have probably noticed, there is a lot of value to completing attending a community college before transferring to a university. In 2012, research found that 71 percent of transfer students (from two-year institutions) earned a bachelor degree within four years of transferring. It is recommended students work with their academic advisor to create a transfer plan and identify courses to take before transferring; this can save you time and money! This handbook will help you as you prepare to transfer to a four year college or university. Source: National Student Clearinghouse Research Center, Transfer Outcomes 2 Missouri College Transfer Guide Your Resource in Planning for YOUR Future Student Rights and Responsibilities ……………………………………………… 4 Missouri Colleges and Universities ………………………………………….……. 5 Finding the Right Career ………………………………………………..…....………. 7 Picking a Major ………………………………………………...…………..…....………. 8 Establishing a Budget …………………………………………………………..…...…. 9 Choosing a Transfer School ………………………………………………....…….. 11 Utilizing Financial Aid & Scholarships………………………...…….....….….. 13 Applying to a University ………………………………………………..….………….
    [Show full text]
  • 2016-2018 Catalog
    2016-2018 CATALOG ► 2016-2018 CATALOG Greetings Contact Info Academic Calendar About Mineral Area College Admissions & Records Support Services Tuition, Financial Assistance Student Life Academic & General College Policies Arts & Sciences Division Career & Technical Education Division Course Descriptions Administration, Faculty Greetings > From the President Greetings CATALOG Greetings From the President Contact Info Hello! Welcome to Mineral Area College’s 2016-18 Catalog. This publication Academic Calendar is an important part of your educational career-- it’s your map, guidebook and passport to the college, all in one. About Mineral Use it to help: Area College ■ Figure out financial aid, Admissions & ■ Find services that aid your journey to completion, Records ■ Choose a major or field of study, Support ■ Register for the right classes, Services ■ Connect with services that help you succeed (counseling, tutoring, etc.), Tuition, ■ Track your progress, Financial Assistance ■ Understand your college’s policies and procedures, ■ Become acquainted with MAC faculty, staff and administration. Student Life Most everything you need to know can be found in this catalog, although Dr. Steven J. Kurtz Academic & President some things do change over time. If you need any clarification or more General College information, please call or e-mail us. We’re here to help you achieve your goals. Policies On behalf of the Board of Trustees, faculty and staff, thank you for Arts & Sciences considering Mineral Area College. Division Very truly yours, Career & Dr. Steven Kurtz Technical Ed. President, Mineral Area College Division Course Descriptions Administration, Faculty DISCLAIMERS AND CONDITIONS is responsible for compliance with the information, regulations implementing Title VI, Title IX, or Section This publication is for information only and does rules, regulations and policies appearing in the general 504, or the Americans with Disabilities Act.
    [Show full text]
  • Missouri's Community Colleges
    Missouri’s Community Colleges School Locations North Central Moberly Area St. Charles MCC St. Louis State Fair Jefferson Co. East Central Mineral Area Ozarks Technical Three Rivers Crowder Crowder College Crowder • Over 2,900 students enrolled at Crowder College in the fall of 2006. Crowder enrollment has increased by 65% since 2000, making them one of the fastest growing state-assisted colleges in Missouri. • With all of this growth, Crowder has maintained an average class size of 17students. An excellent faculty/student ratio helps make instructors more accessible, and Crowder has a tradition of providing students with the type of friendly atmosphere described as the “Crowder Family.” • Crowder students enjoy the personal attention that small class sizes and caring instructors provide. At Crowder College your instructors will know you by name. Crowder College Housing Up to 180 students can live in 14 individual houses with 6 suites in each. Each of the houses have a community area with a sink, microwave, table and four chairs, couch, and lounge chair. Crowder also provides a color television with cable andld a loca l use tlhtelephone ithin the commons area. Each carpeted suite has two bunkable beds, two closets with individual locks, five drawers for storage, and two desks with a chair. It is possible to hook up both phone and cable service in the individual suites if students wish to pay for these services. In addition there are two com ports for access to the internet provided by Crowder College. Stu den ts res iding on campus get a f ree semest er membership at the Freeman Family YMCA located on the Crowder College campus.
    [Show full text]
  • MOACAC Member Colleges for 2020-21 School Year Arkansas
    MOACAC Member Colleges for 2020-21 School Year Arkansas State University Avila University Baker University Ball State University Baylor University Bellarmine University Belmont University Beloit College Benedictine College Blessing-Rieman College of Nursing and Health Sciences Bradley University Brescia University Butler University Central Christian College of the Bible Central Methodist University Centre College Cleveland University-Kansas City Coe College College of the Ozarks Columbia College Columbia College Chicago Cottey College Creighton University Crowder College Culver-Stockton College DePaul University DePauw University Dominican University Donnelly College Drake University Drury University Earlham College East Central College Eastern Illinois University Embry-Riddle Aeronautical University Emporia State University Evangel University Florida Southern College Fontbonne University Franklin College Gettysburg College Goldfarb School of Nursing at Barnes Jewish College Graceland University Grand Canyon University Hannibal-LaGrange Univesity Hanover College Harris-Stowe State University Illinois College Illinois Institute of Technology Illinois State University Illinois Wesleyan University Indian Hills Community College Indiana State University Indiana University Bloomington Indian Hills Community College Iowa State University Iowa Wesleyan University Jefferson College Johnson & Wales University Johnson County Community College Kansas City Art Institute Kansas State University Knox College Lake Forest College Lewis University Lincoln
    [Show full text]
  • MINERAL AREA COLLEGE Baseball Players Signed to Four-Year Colleges
    MINERAL AREA COLLEGE Baseball Players Signed to Four-Year Colleges MAC has a strong tradition of producing quality players at the next level as shown below. 2018 Sophomore Signees Mitch Barrow Indiana State NCAA DI Kollin Stone Arkansas State NCAA DI Trent Pobst SEMO NCAA DI Brian Chandler SIUE NCAA DI Trynt Tompkins Central Baptist College NAIA Andrew Hayden UMSL NCAA DII Stephen Carter UMSL NCAA DII Hayden Helvey Williams Baptist NAIA Travis Turnbough Missouri Baptist NAIA Brendan Anderson University of Illinois-Springfield NCAA DII 2017 Sophomore Signees Jay Blake Webster NCAA DIII Jacob Clark Central Baptist College NAIA Kenton Crawford Southern Illinois Carbondale NCAA DI Hunter Draffen Lindenwood-Belleville NAIA Colby Eckhoff Fontbonne University NCAA DIII Conner Forsythe Missouri S&T NCAA DII Alex Hanft Missouri Baptist NAIA Ethan Reando Lindenwood-Belleville NAIA Cullen Stockley Lindenwood-Belleville NAIA Kollin Stone Central Baptist College NAIA Layton Tenkhoff Central Baptist College NAIA Christian Thrasher University of Missouri St. Louis NCAA DII Chase Urhahn Southeast Missouri State NCAA DI Garrett West Northwest Missouri State NCAA DII Tanner Wetrich University of Iowa NCAA DI Brennan White Williams Baptist College NAIA Devon Wilson Southeast Missouri State NCAA DI Logan Winder Southeast Missouri State NCAA DI 2016 Sophomore Signees Logan Bax University of Arkansas-Pine Bluff NCAA DI Josh Haggerty SEMO NCAA DI Tanner Kulpa Lindenwood NCAA DII Brad Freed Missouri S&T NCAA DII Hayden Strobel Oklahoma Christian NCAA DII Chase
    [Show full text]
  • 1818-Transfer-Report.Pdf
    Transferability Report Updated 2020 REPORT DISCLAIMER The 1818 program does not verify the accuracy or authenticity of the responses from the survey. The report is meant to be a helpful tool, but is not a guarantee how or if the courses taken will be accepted at another institution. The 1818 Program claims no responsibility and provides no guarantee regarding transferring of credits to another institution. It is the student’s responsibility to declare and communicate with prospective institutions regarding the transferability of SLU credit before enrolling as a full time student. It should be noted that if an institution is not listed on this report, it does not mean the institution does not accept SLU credit, rather we have not had alumni either attend or report back the success of their transfer. HOW TO TRANSFER CREDITS Saint Louis University provides transcripts free of charge if printed. Students may request up to five transcripts per day. To request a transcript: 1. Log into mySLU.slu.edu with your SLUnet ID and password. 2. Click on the “Tools” tab 3. Click on “Banner Self-Service” 4. Click on “Student” 5. Click on “Student Records” 6. Click on “Request a Transcript” 7. Select from address Options 1 or 2, and click “Continue” 8. Enter or modify the address information and click “Continue” 9. Enter the number of copies desired and click “Continue” 10. Review the information and click “Submit Request” TRANSFER DECISION APPEAL HELP If an institution denies an 1818 course to be counted for credit, a student should follow the following process to seek help from the 1818 Office to appeal the decision.
    [Show full text]
  • Table of Contents
    Table of Contents Greetings .................. 2 Library .......................... 13 Veterans ....................... 22 Attendance ................... 33 Trustees & Learning Center ............ 14 Vocational Credit Transfer from/to ACCESS Office ............ 14 Rehabilitation ................ 22 Other Colleges .............. 33 Administration ...... 3 Career Planning Center 14 College Funded Transcripts ................... 33 Calendar................... 4 New Traditions ............. 14 Scholarships ................ 23 Release of Transcripts 34 Telephone Numbers 4 Service Learning .......... 14 Outside Aid Reporting Records on Hold ........... 34 About the College .... 5 Summer Session .......... 14 Requirement ................. 23 Student Information Missouri Customized Verification ................... 23 System .......................... 34 History ............................ 5 Training Program .......... 15 Selective Service Enrollment Verification . 34 Philosophy ...................... 5 New Jobs Training Requirement ................. 23 Student Conduct ........... 35 Mission ............................ 6 Program ...................... 15 Financial Aid Student Due Process ... 35 Objectives....................... 6 RTEC ............................. 15 Confidentiality Policy ..... 23 Right to Privacy ............ 35 Accreditation .................. 6 Evening and Student Consumer Right to Know, Security 36 Admissions ............... 7 Weekend Classes ........ 15 Rights Information ......... 23 Civil Rights ...................
    [Show full text]
  • Career Programs of Study
    Houston High School Information Technology Career Cluster Program of Study Template www.houston.k12.mo.us SUGGESTED COURSE OF HIGH SCHOOL STUDY Minimum Graduation Requirements It is suggested that students consider dual credit, articulation, or advanced placement opportunities for postsecondary credit. Required Courses, Elective Houston High School Career Additional Grade English Math Science Social Studies Options Ed Programs Learning Opportunities 9 English I Pre-Alg OR Integrated Science American PE / Health Computer Apps School-Based: Algebra I Fundamentals Fine Arts Career Research Cooperative Education Additional Electives: Internship Intro to Business Job Shadowing Business Law Service Learning Project Other: _____________________________ 10 English II Algebra I OR Biology American History Multimedia Community Based: Algebra II Web Design Mentorship Volunteer Part-time Employment Other: Additional Electives: _____________________________ Accounting I Assessments/Certifications: Technical Skills Attainment (TSA) Other: _ ____________________________ 11 English III Geometry OR Chemistry I OR Government Personal Finance Algebra II Earth Science OR Placement Assessments: Anat. & Phys. OR Compass Test Secondary Additional Electives: PLAN Business Management ACT Accounting II PSAT SAT ASVAB WorkKeys Other: _____________________________ Choice of: Trig OR Dual Credit Bio Psychology Students as Tutors Business Technology 12 College Prep Eng Dual Credit Algebra Chemistry II Sociology Student Organizations: Dual Credit English Advanced Algebra Zoology WWII DECA English 4 Calculus Physics Holocaust FBLA Dual Credit History Additional Electives: FFA Entrepreneurship FCCLA Business Ecnomics SkillsUSA Other: _____________________________ Articulated Credit Dual Credit Revised 8/2/2011 Postsecondary Offerings – For A Complete Listing, go to www.missouriconnections.org Community College Technical School/Training Institution In State Out of State/Other Crowder College Davis Hart Career Center A.T.
    [Show full text]