1 Neutron Scattering and Its Application to Strongly Correlated Systems
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Resolution Neutron Scattering Technique Using Triple-Axis
1 High -resolution neutron scattering technique using triple-axis spectrometers ¢ ¡ ¡ GUANGYONG XU, ¡ * P. M. GEHRING, V. J. GHOSH AND G. SHIRANE ¢ ¡ Physics Department, Brookhaven National Laboratory, Upton, NY 11973, and NCNR, National Institute of Standards and Technology, Gaithersburg, Maryland, 20899. E-mail: [email protected] (Received 0 XXXXXXX 0000; accepted 0 XXXXXXX 0000) Abstract We present a new technique which brings a substantial increase of the wave-vector £ - resolution of triple-axis-spectrometers by matching the measurement wave-vector £ to the ¥§¦©¨ reflection ¤ of a perfect crystal analyzer. A relative Bragg width of can be ¡ achieved with reasonable collimation settings. This technique is very useful in measuring small structural changes and line broadenings that can not be accurately measured with con- ventional set-ups, while still keeping all the strengths of a triple-axis-spectrometer. 1. Introduction Triple-axis-spectrometers (TAS) are widely used in both elastic and inelastic neutron scat- tering measurements to study the structures and dynamics in condensed matter. It has the £ flexibility to allow one to probe nearly all coordinates in energy ( ) and momentum ( ) space in a controlled manner, and the data can be easily interpreted (Bacon, 1975; Shirane et al., 2002). The resolution of a triple-axis-spectrometer is determined by many factors, including the ¨ incident (E ) and final (E ) neutron energies, the wave-vector transfer , the monochromator PREPRINT: Acta Crystallographica Section A A Journal of the International Union of Crystallography 2 and analyzer mosaic, and the beam collimations, etc. This has been studied in detail by Cooper & Nathans (1967), Werner & Pynn (1971) and Chesser & Axe (1973). -

Neutron Scattering
Neutron Scattering John R.D. Copley Summer School on Methods and Applications of High Resolution Neutron Spectroscopy and Small Angle Neutron Scattering NIST Center for NeutronNCNR Summer Research, School 2011 June 12-16, 2011 Acknowledgements National Science Foundation NIST Center for Neutron (grant # DMR-0944772) Research (NCNR) Center for High Resolution Neutron Scattering (CHRNS) 2 NCNR Summer School 2011 (Slow) neutron interactions Scattering plus Absorption Total =+Elastic Inelastic scattering scattering scattering (diffraction) (spectroscopy) includes “Quasielastic neutron Structure Dynamics scattering” (QENS) NCNR Summer School 2011 3 Total, elastic, and inelastic scattering Incident energy Ei E= Ei -Ef Scattered energy Ef (“energy transfer”) Total scattering: Elastic scattering: E = E (i.e., E = 0) all Ef (i.e., all E) f i Inelastic scattering: E ≠ E (i.e., E ≠ 0) D f i A M M Ef Ei S Ei D S Diffractometer Spectrometer (Some write E = Ef –Ei) NCNR Summer School 2011 4 Kinematics mv= = k 1 222 Emvk2m==2 = Scattered wave (m is neutron’s mass) vector k , energy E 2θ f f Incident wave vector ki, energy Ei N.B. The symbol for scattering angle in Q is wave vector transfer, SANS experiments is or “scattering vector” Q =Q is momentum transfer θ, not 2θ. Q = ki - kf (For x-rays, Eck = = ) (“wave vector transfer”) NCNR Summer School 2011 5 Elastic scattering Q = ki - kf G In real space k In reciprocal space f G G G kf Q ki 2θ 2θ G G k Q i E== 0 kif k Q =θ 2k i sin NCNR Summer School 2011 6 Total scattering, inelastic scattering Q = ki - kf G kf G Q Qkk2kkcos2222= +− θ 2θ G if if ki At fixed scattering angle 2θ, the magnitude (and the direction) of Q varies with the energy transfer E. -

Neutron Scattering
Neutron Scattering Basic properties of neutron and electron neutron electron −27 −31 mass mkn =×1.675 10 g mke =×9.109 10 g charge 0 e spin s = ½ s = ½ −e= −e= magnetic dipole moment µnn= gs with gn = 3.826 µee= gs with ge = 2.0 2mn 2me =22k 2π =22k Ek== E = 2m λ 2m energy n e 81.81 150.26 Em[]eV = 2 Ee[]V = 2 λ ⎣⎡Å⎦⎤ λ ⎣⎦⎡⎤Å interaction with matter: Coulomb interaction — 9 strong-force interaction 9 — magnetic dipole-dipole 9 9 interaction Several salient features are apparent from this table: – electrons are charged and experience strong, long-range Coulomb interactions in a solid. They therefore typically only penetrate a few atomic layers into the solid. Electron scattering is therefore a surface-sensitive probe. Neutrons are uncharged and do not experience Coulomb interaction. The strong-force interaction is naturally strong but very short-range, and the magnetic interaction is long-range but weak. Neutrons therefore penetrate deeply into most materials, so that neutron scattering is a bulk probe. – Electrons with wavelengths comparable to interatomic distances (λ ~2Å ) have energies of several tens of electron volts, comparable to energies of plasmons and interband transitions in solids. Electron scattering is therefore well suited as a probe of these high-energy excitations. Neutrons with λ ~2Å have energies of several tens of meV , comparable to the thermal energies kTB at room temperature. These so-called “thermal neutrons” are excellent probes of low-energy excitations such as lattice vibrations and spin waves with energies in the meV range. -

Spallation Neutron Sources for Science and Technology
Proceedings of the 8th Conference on Nuclear and Particle Physics, 20-24 Nov. 2011, Hurghada, Egypt SPALLATION NEUTRON SOURCES FOR SCIENCE AND TECHNOLOGY M.N.H. Comsan Nuclear Research Center, Atomic Energy Authority, Egypt Spallation Neutron Facilities Increasing interest has been noticed in spallation neutron sources (SNS) during the past 20 years. The system includes high current proton accelerator in the GeV region and spallation heavy metal target in the Hg-Bi region. Among high flux currently operating SNSs are: ISIS in UK (1985), SINQ in Switzerland (1996), JSNS in Japan (2008), and SNS in USA (2010). Under construction is the European spallation source (ESS) in Sweden (to be operational in 2020). The intense neutron beams provided by SNSs have the advantage of being of non-reactor origin, are of continuous (SINQ) or pulsed nature. Combined with state-of-the-art neutron instrumentation, they have a diverse potential for both scientific research and diverse applications. Why Neutrons? Neutrons have wavelengths comparable to interatomic spacings (1-5 Å) Neutrons have energies comparable to structural and magnetic excitations (1-100 meV) Neutrons are deeply penetrating (bulk samples can be studied) Neutrons are scattered with a strength that varies from element to element (and isotope to isotope) Neutrons have a magnetic moment (study of magnetic materials) Neutrons interact only weakly with matter (theory is easy) Neutron scattering is therefore an ideal probe of magnetic and atomic structures and excitations Neutron Producing Reactions -

Single Crystal Diffuse Neutron Scattering
Review Single Crystal Diffuse Neutron Scattering Richard Welberry 1,* ID and Ross Whitfield 2 ID 1 Research School of Chemistry, Australian National University, Canberra, ACT 2601, Australia 2 Neutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA; whitfi[email protected] * Correspondence: [email protected]; Tel.: +61-2-6125-4122 Received: 30 November 2017; Accepted: 8 January 2018; Published: 11 January 2018 Abstract: Diffuse neutron scattering has become a valuable tool for investigating local structure in materials ranging from organic molecular crystals containing only light atoms to piezo-ceramics that frequently contain heavy elements. Although neutron sources will never be able to compete with X-rays in terms of the available flux the special properties of neutrons, viz. the ability to explore inelastic scattering events, the fact that scattering lengths do not vary systematically with atomic number and their ability to scatter from magnetic moments, provides strong motivation for developing neutron diffuse scattering methods. In this paper, we compare three different instruments that have been used by us to collect neutron diffuse scattering data. Two of these are on a spallation source and one on a reactor source. Keywords: single crystal; diffuse scattering; neutrons; spallation source; time-of-flight 1. Introduction Bragg scattering, which is used in conventional crystallography, gives only information about the average crystal structure. Diffuse scattering from single crystals, on the other hand, is a prime source of local structural information. There is now a wealth of evidence to show that the more local structure is investigated the more we are obliged to reassess our understanding of crystalline structure and behaviour [1]. -

Basics of Neutron Scattering
Part I Basics of neutron scattering 13 Chapter 1 Introduction to neutron scattering Neutron scattering is one of the most powerful and versatile experimental meth- ods to study the structure and dynamics of materials on the atomic and nanome- ter scale. Quoting the Nobel committee, when awarding the prize to C. Shull and B. Brockhouse in 1994, these pioneers have “helped answer the question of where atoms are and ... the question of what atoms do” [4]. Neutron scattering is presently used by more than 5000 researchers world- wide, and the scope of the method is continuously broadening. In the 1950’ies and 1960’ies, neutron scattering was an exotic tool in Solid State Physics and Chemical Crystallography, but today it serves communities as diverse as Biol- ogy, Earth Sciences, Planetary Science, Engineering, Polymer Chemistry, and Cultural Heritage. In brief, neutrons are used in all scientific fields that deal with hard, soft, or biological materials. It is, however, appropriate to issue a warning already here. Although neu- tron scattering is a great technique, it is also time-consuming and expensive. Neutron scattering experiments last from hours to days and are performed at large international facilities. Here, the running costs correspond to several thou- sand Euros per instrument day. Hence, neutron scattering should be used only where other methods are inadequate. For the study of atomic and nanometer-scale structure in materials, X-ray scattering is the technique of choice. X-ray sources are by far more abundant and are, especially for synchrotron X-ray sources, much stronger than neutron sources. Hence, the rule of thumb goes: “If an experiment can be performed with X-rays, use X-rays”. -

Opportunities and Challenges in Neutron Crystallography
EPJ Web of Conferences 236, 02001 (2020) https://doi.org/10.1051/epjconf/202023602001 JDN 24 Opportunities and challenges in neutron crystallography Nathan Richard Zaccai1,*, and Nicolas Coquelle2,† 1CIMR, University of Cambridge, Cambridge CB2 0XY, United Kingdom 2Institut Laue Langevin, 38042 Grenoble Cedex 9, France Abstract. Neutron and X-ray crystallography are complementary to each other. While X-ray scattering is directly proportional to the number of electrons of an atom, neutrons interact with the atomic nuclei themselves. Neutron crystallography therefore provides an excellent alternative in determining the positions of hydrogens in a biological molecule. In particular, since highly polarized hydrogen atoms (H+) do not have electrons, they cannot be observed by X-rays. Neutron crystallography has its own limitations, mainly due to inherent low flux of neutrons sources, and as a consequence, the need for much larger crystals and for different data collection and analysis strategies. These technical challenges can however be overcome to yield crucial structural insights about protonation states in enzyme catalysis, ligand recognition, as well as the presence of unusual hydrogen bonds in proteins. 1 Introduction Although X-ray crystallography has become the workhorse of structural biology, Neutron crystallography has several advantages to offer in the structural analysis of biological molecules. X-rays and neutrons interact differently with matter in general, and with biological macromolecules in particular. These two crystallography approaches are therefore complementary to each other [1]. While X-ray scattering is directly proportional to the number of electrons of an atom, neutrons interact with the atomic nuclei themselves. In this perspective, hydrogen atoms, which represent ~50% of the atomistic composition of proteins and DNA, are hardly visible using X-ray crystallography, while they can be observed in nuclear density maps derived from neutron diffraction data even at moderate resolution (2.5Å and higher). -
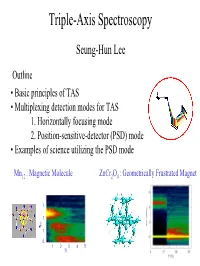
Triple-Axis Spectroscopy
Triple-Axis Spectroscopy Seung-Hun Lee Outline • Basic principles of TAS • Multiplexing detection modes for TAS 1. Horizontally focusing mode 2. Position-sensitive-detector (PSD) mode • Examples of science utilizing the PSD mode Mn12 : Magnetic Molecule ZnCr2O4 : Geometrically Frustrated Magnet 1. 1. ω h 1. 0. 12345 T( Neutron Scattering Sample ? Incident neutrons Scattered neutrons measures scattering cross section as a function of Q and ω 2 d σ (Q,ω) dΩdω Neutron Scattering Correlation Function Cross Section 2 Fourier Transform d σ < S (t) S (0) > dΩdω R R Ordered moment Fluctuating moment 0 Γ ~ h/τ 0 Time ω Long range order Short range order κ ~ 1/ξ Q R-R Γ : relaxation time τ : lifetime κ : intrinsic linewidth ξ : correlation length How can we determine Q and ω ? Scattering triangle : Energy and momentum are conserved in the scattering process Now, how to determine ki, kf, and 2θ ? • Triple-axis spectroscopy (TAS) • Time-of-flight spectroscopy (TOF) Conventional Triple-Axis Spectroscopy (TAS) A single point at a time Sample Single Detector Neutron Source Analyzer Monochromator TAS is ideally suited for probing small regions of phase space Shortcoming: Low data collection rate Improvement Multicrystal analyzer and position-sensitive detector Horizontally Focusing (HF) Analyzer Mode Sample Relaxed Q-resolution Monochromator Single Detector ∆2θ Multicrystal Analyzer L = distance from sample to HF analyzer wa = total width of HF analyzer ∆2θ =wa sinθa/L ~ 9 degree for Ef=5 meV at SPINS Useful for studying systems with short-range correlations -

Dynamics and Neutron Scattering
Introduction to Neutron Spectroscopy John R.D. Copley Summer School on the Fundamentals of Neutron Scattering NIST Center for Neutron Research, June 8-12, 2015 NCNR Summer School, 2015 Neutron scattering Neutron scattering is an experimental technique that is used to reveal information about the structure and dynamics of materials. When a neutron strikes a material object and leaves in a new direction it is said to have been scattered. Its momentum is changed and there may also be a change in its kinetic energy. In a neutron scattering experiment a sample is placed in a beam from a neutron source, and some of the scattered neutrons are counted. NCNR Summer School, 2015 Neutron scattering There are two main types of neutron scattering experiments. (1) Neutron diffraction experiments, Ei is incident energy which give structural information, Ef is scattered energy e.g. D M (2) Neutron spectroscopy experiments, which give dynamical information, e.g. Ei A S Ef M: monochromator M S: sample D: detector Ei D S A: analyzer NCNR Summer School, 2015 Recognition Clifford G. Shull Bertram N. Brockhouse (Neutron Diffraction) (Neutron Spectroscopy) The importance of these techniques was recognized by the Royal Swedish Academy of Sciences who in 1994 awarded the Nobel Prize in Physics to two scientists “for pioneering contributions to the development of neutron scattering techniques for studies of condensed matter”. The Prize was shared between Professor Clifford G. Shull of MIT, “for the development of the neutron diffraction technique”, and Professor Bertram N. Brockhouse of McMaster University (Canada), “for the development of neutron spectroscopy”. -

Neutron Spin Echo Spectroscopy
Neutron Spin Echo Spectroscopy Peter Fouquet [email protected] Institut Laue-Langevin Grenoble, France September 2014 Hercules Specialized Course 17 - Grenoble What you are supposed to learn in this lecture 1. The length and time scales that can be studied using NSE spectroscopy 2. The measurement principle of NSE spectroscopy 3. Discrimination techniques for coherent, incoherent and magnetic dynamics 4. To which scientific problems can I apply NSE spectroscopy? The measurement principle of neutron spin echo spectroscopy (quantum mechanical model) The neutron wave function is split by magnetic fields magnetic coil 1 magnetic coil 2 polarised sample The 2 wave packets arrive at neutron the sample with a time difference t If the molecules move between the arrival of the first and second wave packet then coherence is lost t λ3 Bdl The intermediate ∝ scattering function I(Q,t) reflects this loss in coherence strong wavelength field integral dependence The measurement principle of neutron spin echo spectroscopy Dynamic Scattering NSE spectra for diffusive motion Function S(Q,ω) G(R,ω) I(Q,t) = e-t/τ Fourier Transforms temperature up ⇒ τ down Intermediate VanHove Correlation Scattering Function Function I(Q,t) G(R,t) Measured with Neutron Spin Echo (NSE) Spectroscopy Neutron spin echo spectroscopy in the time/space landscape NSE is the neutron spectroscopy with the highest energy resolution The time range covered is 1 ps < t < 1 µs (equivalent to neV energy resolution) The momentum transfer range is 0.01 < Q < 4 Å-1 Spin Echo The measurement principle -

Neutron Scattering with a Triple-Axis Spectrometer Basic Techniques
Neutron Scattering with a Triple-Axis Spectrometer Basic Techniques Gen Shirane, Stephen M. Shapiro, and John M. Tranquada Brookhaven National Laboratory published by the press syndicate of the university of cambridge The Pitt Building, Trumpington Street, Cambridge, United Kingdom cambridge university press The Edinburgh Building, Cambridge, CB2 2RU, UK 40 West 20th Street, New York, NY 10011–4211, USA 477 Williamstown Road, Port Melbourne, VIC 3207, Australia Ruizde Alarc on´ 13, 28014 Madrid, Spain Dock House, The Waterfront, Cape Town 8001, South Africa http://www.cambridge.org c Cambridge University Press 2002 This book is in copyright. Subject to statutory exception and to the provisions of relevant collective licensing agreements, no reproduction of any part may take place without the written permission of Cambridge University Press. First published 2002 Printed in the United Kingdom at the University Press, Cambridge Typeface Times 10/13pt System LATEX [UPH] A catalogue record of this book is available from the British Library Library of Congress Cataloguing in Publication data Shirane, G. Neutron scattering with a triple-axis spectrometer / Gen Shirane, Stephen M. Shapiro, and John M. Tranquada. p. cm. ISBN 0 521 41126 2 1. Neutrons–Scattering. I. Shapiro, S. M. (Stephen M.), 1941– II. Tranquada, John M., 1955– III. Title. QC793.5.N4628 S47 2002 539.7’213–dc21 2001035050 ISBN 0 521 41126 2 hardback Contents Preface page ix 1 Introduction 1 1.1 Properties of thermal neutrons 1 1.2 Neutron sources 4 1.3 Reciprocal space and scattering diagram 11 1.3.1 Elastic scattering 12 1.3.2 Inelastic scattering 14 1.4 Neutron scattering instruments 15 1.4.1 Three-axis instrument 15 1.4.2 Time-of-flight (TOF) instrument 16 1.4.3 Backscattering and neutron spin echo (NSE) 17 References 18 2 Scattering formulas 20 2.1 Introduction 20 2.2 Fermi’s Golden Rule and the Born approximation 21 2.3 Coherent vs. -

The Basics of Neutron Spin Echo Bela Farago ILL - Grenoble
The basics of Neutron Spin Echo Bela Farago ILL - Grenoble Introduction Until 1974 inelastic neutron scattering consisted of producing by some means a neutron beam of known speed and measuring the final speed of the neutrons after the scattering event. The smaller the energy change was, the better the neutron speed had to be defined. As the neutrons come form a reactor with an approximately Maxwell distribution, an infinitely good energy resolution can be achieved only at the expense of infinitely low count rate. This introduces a practical resolution limit around 0.1|jeV on back- scattering instuments. In 1972 F. Mezei discovered the method of Neutron Spin Echo. this method decouples the energy resolution from intensity loss. Basics It can be shown [1] that an ensemble of polarized particle with a magnetic moment and 1/2 spin behaves exactly like a classical magnetic moment. Entering a region with a magnetic field perpendicular to its magnetic moment it will undergo Larmor precession. In the case of neutrons: (o-yB where B is the magnetic field, CD is the frequency of rotation and ^=2.916kHz/Oe is the gyromagnetic ratio of the neutron. When the magnetic field changes its direction relative to the neutron trajectory two limiting cases have to be distinguished: 1) Adiabatic change, when the change of the magnetic field direction (as seen by the neutron) is slow compared to the Larmor precession. In this case the component of the beam polarization which was parallel to the magnetic field will be maintained and it will follow the field direction.