Program Design by Calculation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Mathematics Calculation Policy ÷
Mathematics Calculation Policy ÷ Commissioned by The PiXL Club Ltd. June 2016 This resource is strictly for the use of member schools for as long as they remain members of The PiXL Club. It may not be copied, sold nor transferred to a third party or used by the school after membership ceases. Until such time it may be freely used within the member school. All opinions and contributions are those of the authors. The contents of this resource are not connected with nor endorsed by any other company, organisation or institution. © Copyright The PiXL Club Ltd, 2015 About PiXL’s Calculation Policy • The following calculation policy has been devised to meet requirements of the National Curriculum 2014 for the teaching and learning of mathematics, and is also designed to give pupils a consistent and smooth progression of learning in calculations across the school. • Age stage expectations: The calculation policy is organised according to age stage expectations as set out in the National Curriculum 2014 and the method(s) shown for each year group should be modelled to the vast majority of pupils. However, it is vital that pupils are taught according to the pathway that they are currently working at and are showing to have ‘mastered’ a pathway before moving on to the next one. Of course, pupils who are showing to be secure in a skill can be challenged to the next pathway as necessary. • Choosing a calculation method: Before pupils opt for a written method they should first consider these steps: Should I use a formal Can I do it in my Could I use -

Program #6: Word Count
CSc 227 — Program Design and Development Spring 2014 (McCann) http://www.cs.arizona.edu/classes/cs227/spring14/ Program #6: Word Count Due Date: March 11 th, 2014, at 9:00 p.m. MST Overview: The UNIX operating system (and its variants, of which Linux is one) includes quite a few useful utility programs. One of those is wc, which is short for Word Count. The purpose of wc is to give users an easy way to determine the size of a text file in terms of the number of lines, words, and bytes it contains. (It can do a bit more, but that’s all of the functionality that we are concerned with for this assignment.) Counting lines is done by looking for “end of line” characters (\n (ASCII 10) for UNIX text files, or the pair \r\n (ASCII 13 and 10) for Windows/DOS text files). Counting words is also straight–forward: Any sequence of characters not interrupted by “whitespace” (spaces, tabs, end–of–line characters) is a word. Of course, whitespace characters are characters, and need to be counted as such. A problem with wc is that it generates a very minimal output format. Here’s an example of what wc produces on a Linux system when asked to count the content of a pair of files; we can do better! $ wc prog6a.dat prog6b.dat 2 6 38 prog6a.dat 32 321 1883 prog6b.dat 34 327 1921 total Assignment: Write a Java program (completely documented according to the class documentation guidelines, of course) that counts lines, words, and bytes (characters) of text files. -
Administering Unidata on UNIX Platforms
C:\Program Files\Adobe\FrameMaker8\UniData 7.2\7.2rebranded\ADMINUNIX\ADMINUNIXTITLE.fm March 5, 2010 1:34 pm Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta UniData Administering UniData on UNIX Platforms UDT-720-ADMU-1 C:\Program Files\Adobe\FrameMaker8\UniData 7.2\7.2rebranded\ADMINUNIX\ADMINUNIXTITLE.fm March 5, 2010 1:34 pm Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Beta Notices Edition Publication date: July, 2008 Book number: UDT-720-ADMU-1 Product version: UniData 7.2 Copyright © Rocket Software, Inc. 1988-2010. All Rights Reserved. Trademarks The following trademarks appear in this publication: Trademark Trademark Owner Rocket Software™ Rocket Software, Inc. Dynamic Connect® Rocket Software, Inc. RedBack® Rocket Software, Inc. SystemBuilder™ Rocket Software, Inc. UniData® Rocket Software, Inc. UniVerse™ Rocket Software, Inc. U2™ Rocket Software, Inc. U2.NET™ Rocket Software, Inc. U2 Web Development Environment™ Rocket Software, Inc. wIntegrate® Rocket Software, Inc. Microsoft® .NET Microsoft Corporation Microsoft® Office Excel®, Outlook®, Word Microsoft Corporation Windows® Microsoft Corporation Windows® 7 Microsoft Corporation Windows Vista® Microsoft Corporation Java™ and all Java-based trademarks and logos Sun Microsystems, Inc. UNIX® X/Open Company Limited ii SB/XA Getting Started The above trademarks are property of the specified companies in the United States, other countries, or both. All other products or services mentioned in this document may be covered by the trademarks, service marks, or product names as designated by the companies who own or market them. License agreement This software and the associated documentation are proprietary and confidential to Rocket Software, Inc., are furnished under license, and may be used and copied only in accordance with the terms of such license and with the inclusion of the copyright notice. -

Thomas Ströhlein's Endgame Tables: a 50Th Anniversary
Thomas Ströhlein's Endgame Tables: a 50th Anniversary Article Supplemental Material The Festschrift on the 40th Anniversary of the Munich Faculty of Informatics Haworth, G. (2020) Thomas Ströhlein's Endgame Tables: a 50th Anniversary. ICGA Journal, 42 (2-3). pp. 165-170. ISSN 1389-6911 doi: https://doi.org/10.3233/ICG-200151 Available at http://centaur.reading.ac.uk/90000/ It is advisable to refer to the publisher’s version if you intend to cite from the work. See Guidance on citing . Published version at: https://content.iospress.com/articles/icga-journal/icg200151 To link to this article DOI: http://dx.doi.org/10.3233/ICG-200151 Publisher: The International Computer Games Association All outputs in CentAUR are protected by Intellectual Property Rights law, including copyright law. Copyright and IPR is retained by the creators or other copyright holders. Terms and conditions for use of this material are defined in the End User Agreement . www.reading.ac.uk/centaur CentAUR Central Archive at the University of Reading Reading’s research outputs online 40 Jahre Informatik in Munchen:¨ 1967 – 2007 Festschrift Herausgegeben von Friedrich L. Bauer unter Mitwirkung von Helmut Angstl, Uwe Baumgarten, Rudolf Bayer, Hedwig Berghofer, Arndt Bode, Wilfried Brauer, Stephan Braun, Manfred Broy, Roland Bulirsch, Hans-Joachim Bungartz, Herbert Ehler, Jurgen¨ Eickel, Ursula Eschbach, Anton Gerold, Rupert Gnatz, Ulrich Guntzer,¨ Hellmuth Haag, Winfried Hahn (†), Heinz-Gerd Hegering, Ursula Hill-Samelson, Peter Hubwieser, Eike Jessen, Fred Kroger,¨ Hans Kuß, Klaus Lagally, Hans Langmaack, Heinrich Mayer, Ernst Mayr, Gerhard Muller,¨ Heinrich Noth,¨ Manfred Paul, Ulrich Peters, Hartmut Petzold, Walter Proebster, Bernd Radig, Angelika Reiser, Werner Rub,¨ Gerd Sapper, Gunther Schmidt, Fred B. -
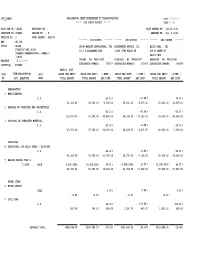
Bid Check Report * * * Time: 14:04
DOT_RGGB01 WASHINGTON STATE DEPARTMENT OF TRANSPORTATION DATE: 05/28/2013 * * * BID CHECK REPORT * * * TIME: 14:04 PS &E JOB NO : 11W101 REVISION NO : BIDS OPENED ON : Jun 26 2013 CONTRACT NO : 008498 REGION NO : 9 AWARDED ON : Jul 1 2013 VERSION NO : 2 WORK ORDER# : XL4078 ------- LOW BIDDER ------- ------- 2ND BIDDER ------- ------- 3RD BIDDER ------- HWY : SR 104 TITLE : SR104 ORION MARINE CONTRACTORS, INC. BLACKWATER MARINE, LLC QUIGG BROS., INC. KINGSTON TML SLIPS 1112 E ALEXANDER AVE 12019 76TH PLACE NE 819 W STATE ST DOLPHIN PRESERVATION - PHASE 4 98520-5934 11W101 PROJECT : NH-2013(079) TACOMA WA 984214102 KIRKLAND WA 980342437 ABERDEEN WA 985200281 COUNTY(S) : KITSAP CONTRACTOR NUMBER : 100767 CONTRACTOR NUMBER : 100874 CONTRACTOR NUMBER : 680000 ENGR'S. EST. ITEM ITEM DESCRIPTION UNIT PRICE PER UNIT/ PRICE PER UNIT/ % DIFF./ PRICE PER UNIT/ % DIFF./ PRICE PER UNIT/ % DIFF./ NO. EST. QUANTITY MEAS TOTAL AMOUNT TOTAL AMOUNT AMT.DIFF. TOTAL AMOUNT AMT.DIFF. TOTAL AMOUNT AMT.DIFF. PREPARATION 1 MOBILIZATION L.S. -25.20 % -25.48 % 40.00 % 25,000.00 18,700.00 -6,300.00 18,630.00 -6,370.00 35,000.00 10,000.00 2 REMOVAL OF STRUCTURE AND OBSTRUCTION L.S. -56.10 % -65.08 % -56.71 % 115,500.00 50,700.00 -64,800.00 40,338.00 -75,162.00 50,000.00 -65,500.00 3 DISPOSAL OF CREOSOTED MATERIAL L.S. -21.05 % -8.99 % -15.79 % 47,500.00 37,500.00 -10,000.00 43,228.35 -4,271.65 40,000.00 -7,500.00 STRUCTURE 4 STRUCTURAL LOW ALLOY STEEL - DOLPHINS L.S. -

HEP Computing Part I Intro to UNIX/LINUX Adrian Bevan
HEP Computing Part I Intro to UNIX/LINUX Adrian Bevan Lectures 1,2,3 [email protected] 1 Lecture 1 • Files and directories. • Introduce a number of simple UNIX commands for manipulation of files and directories. • communicating with remote machines [email protected] 2 What is LINUX • LINUX is the operating system (OS) kernel. • Sitting on top of the LINUX OS are a lot of utilities that help you do stuff. • You get a ‘LINUX distribution’ installed on your desktop/laptop. This is a sloppy way of saying you get the OS bundled with lots of useful utilities/applications. • Use LINUX to mean anything from the OS to the distribution we are using. • UNIX is an operating system that is very similar to LINUX (same command names, sometimes slightly different functionalities of commands etc). – There are usually enough subtle differences between LINUX and UNIX versions to keep you on your toes (e.g. Solaris and LINUX) when running applications on multiple platforms …be mindful of this if you use other UNIX flavours. – Mac OS X is based on a UNIX distribution. [email protected] 3 Accessing a machine • You need a user account you should all have one by now • can then log in at the terminal (i.e. sit in front of a machine and type in your user name and password to log in to it). • you can also log in remotely to a machine somewhere else RAL SLAC CERN London FNAL in2p3 [email protected] 4 The command line • A user interfaces with Linux by typing commands into a shell. -

Humidity Definitions
ROTRONIC TECHNICAL NOTE Humidity Definitions 1 Relative humidity Table of Contents Relative humidity is the ratio of two pressures: %RH = 100 x p/ps where p is 1 Relative humidity the actual partial pressure of the water vapor present in the ambient and ps 2 Dew point / Frost the saturation pressure of water at the temperature of the ambient. point temperature Relative humidity sensors are usually calibrated at normal room temper - 3 Wet bulb ature (above freezing). Consequently, it generally accepted that this type of sensor indicates relative humidity with respect to water at all temperatures temperature (including below freezing). 4 Vapor concentration Ice produces a lower vapor pressure than liquid water. Therefore, when 5 Specific humidity ice is present, saturation occurs at a relative humidity of less than 100 %. 6 Enthalpy For instance, a humidity reading of 75 %RH at a temperature of -30°C corre - 7 Mixing ratio sponds to saturation above ice. by weight 2 Dew point / Frost point temperature The dew point temperature of moist air at the temperature T, pressure P b and mixing ratio r is the temperature to which air must be cooled in order to be saturated with respect to water (liquid). The frost point temperature of moist air at temperature T, pressure P b and mixing ratio r is the temperature to which air must be cooled in order to be saturated with respect to ice. Magnus Formula for dew point (over water): Td = (243.12 x ln (pw/611.2)) / (17.62 - ln (pw/611.2)) Frost point (over ice): Tf = (272.62 x ln (pi/611.2)) / (22.46 - -

An Arbitrary Precision Computation Package David H
ARPREC: An Arbitrary Precision Computation Package David H. Bailey, Yozo Hida, Xiaoye S. Li and Brandon Thompson1 Lawrence Berkeley National Laboratory, Berkeley, CA 94720 Draft Date: 2002-10-14 Abstract This paper describes a new software package for performing arithmetic with an arbitrarily high level of numeric precision. It is based on the earlier MPFUN package [2], enhanced with special IEEE floating-point numerical techniques and several new functions. This package is written in C++ code for high performance and broad portability and includes both C++ and Fortran-90 translation modules, so that conventional C++ and Fortran-90 programs can utilize the package with only very minor changes. This paper includes a survey of some of the interesting applications of this package and its predecessors. 1. Introduction For a small but growing sector of the scientific computing world, the 64-bit and 80-bit IEEE floating-point arithmetic formats currently provided in most computer systems are not sufficient. As a single example, the field of climate modeling has been plagued with non-reproducibility, in that climate simulation programs give different results on different computer systems (or even on different numbers of processors), making it very difficult to diagnose bugs. Researchers in the climate modeling community have assumed that this non-reproducibility was an inevitable conse- quence of the chaotic nature of climate simulations. Recently, however, it has been demonstrated that for at least one of the widely used climate modeling programs, much of this variability is due to numerical inaccuracy in a certain inner loop. When some double-double arithmetic rou- tines, developed by the present authors, were incorporated into this program, almost all of this variability disappeared [12]. -

Neural Correlates of Arithmetic Calculation Strategies
Cognitive, Affective, & Behavioral Neuroscience 2009, 9 (3), 270-285 doi:10.3758/CABN.9.3.270 Neural correlates of arithmetic calculation strategies MIRIA M ROSENBERG -LEE Stanford University, Palo Alto, California AND MARSHA C. LOVETT AND JOHN R. ANDERSON Carnegie Mellon University, Pittsburgh, Pennsylvania Recent research into math cognition has identified areas of the brain that are involved in number processing (Dehaene, Piazza, Pinel, & Cohen, 2003) and complex problem solving (Anderson, 2007). Much of this research assumes that participants use a single strategy; yet, behavioral research finds that people use a variety of strate- gies (LeFevre et al., 1996; Siegler, 1987; Siegler & Lemaire, 1997). In the present study, we examined cortical activation as a function of two different calculation strategies for mentally solving multidigit multiplication problems. The school strategy, equivalent to long multiplication, involves working from right to left. The expert strategy, used by “lightning” mental calculators (Staszewski, 1988), proceeds from left to right. The two strate- gies require essentially the same calculations, but have different working memory demands (the school strategy incurs greater demands). The school strategy produced significantly greater early activity in areas involved in attentional aspects of number processing (posterior superior parietal lobule, PSPL) and mental representation (posterior parietal cortex, PPC), but not in a numerical magnitude area (horizontal intraparietal sulcus, HIPS) or a semantic memory retrieval area (lateral inferior prefrontal cortex, LIPFC). An ACT–R model of the task successfully predicted BOLD responses in PPC and LIPFC, as well as in PSPL and HIPS. A central feature of human cognition is the ability to strategy use) and theoretical (parceling out the effects of perform complex tasks that go beyond direct stimulus– strategy-specific activity). -

Useful Tai Ls Dino
SCIENCE & NATURE Useful Tails Materials Pictures of a possum, horse, lizard, rattlesnake, peacock, fish, bird, and beaver What to do 1. Display the animal pictures so the children can see them. 2. Say the following sentences. Ask the children to guess the animal by the usefulness of its tail. I use my tail for hanging upside down. (possum) I use my tail as a fly swatter. (horse) When my tail breaks off, I grow a new one. (lizard) I shake my noisy tail when I am about to strike. (rattlesnake) My tail opens like a beautiful fan. (peacock) I use my tail as a propeller. I cannot swim without it. (fish) I can’t fly without my tail. (bird) I use my powerful tail for building. (beaver) More to do Ask the children if they can name other animals that have tails. Ask them how these animals’Downloaded tails might by [email protected] useful. from Games: Cut out the tailsProFilePlanner.com of each of the animals. Encourage the children to pin the tails on the pictures (like “Pin the Tail on the Donkey”). Dotti Enderle, Richmond, TX Dino Dig Materials Plastic or rubber dinosaurs or bones Sand Wide-tip, medium-sized paintbrushes Plastic sand shovels Small plastic buckets Clipboards Paper Pencil or pens 508 The GIANT Encyclopedia of Preschool Activities for Four-Year-Olds Downloaded by [email protected] from ProFilePlanner.com SCIENCE & NATURE What to do 1. Beforehand, hide plastic or rubber dinosaurs or bones in the sand. 2. Give each child a paintbrush, shovel, and bucket. 3. -

Georgia Department of Revenue
Form MV-9W (Rev. 6-2015) Web and MV Manual Georgia Department of Revenue - Motor Vehicle Division Request for Manufacture of a Special Veteran License Plate ______________________________________________________________________________________ Purpose of this Form: This form is to be used to apply for a military license plate/tag. This form should not be used to record a change of ownership, change of address, or change of license plate classification. Required documentation: You must provide a legible copy of your service discharge (DD-214, DD-215, or for World War II veterans, a WD form) indicating your branch and term of service. If you are an active duty member, a copy of the approved documentation supporting your current membership in the respective reserve or National Guard unit is required. In the case of a retired reserve member from that unit, you must furnish approved documentation supporting the current retired membership status from that reserve unit. OWNER INFORMATION First Name Middle Initial Last Name Suffix Owners’ Full Legal Name: Mailing Address: City: State: Zip: Telephone Number: Owner(s)’ Full Legal Name: First Name Middle Initial Last Name Suffix If secondary Owner(s) are listed Mailing Address: City: State: Zip: Telephone Number: VEHICLE INFORMATION Passenger Vehicle Motorcycle Private Truck Vehicle Identification Number (VIN): Year: Make: Model: CAMPAIGN/TOUR of DUTY Branch of Service: SERVICE AWARD Branch of Service: LICENSE PLATES ______________________ LICENSE PLATES ______________________ World War I World -

The Linux Command Line
The Linux Command Line Fifth Internet Edition William Shotts A LinuxCommand.org Book Copyright ©2008-2019, William E. Shotts, Jr. This work is licensed under the Creative Commons Attribution-Noncommercial-No De- rivative Works 3.0 United States License. To view a copy of this license, visit the link above or send a letter to Creative Commons, PO Box 1866, Mountain View, CA 94042. A version of this book is also available in printed form, published by No Starch Press. Copies may be purchased wherever fine books are sold. No Starch Press also offers elec- tronic formats for popular e-readers. They can be reached at: https://www.nostarch.com. Linux® is the registered trademark of Linus Torvalds. All other trademarks belong to their respective owners. This book is part of the LinuxCommand.org project, a site for Linux education and advo- cacy devoted to helping users of legacy operating systems migrate into the future. You may contact the LinuxCommand.org project at http://linuxcommand.org. Release History Version Date Description 19.01A January 28, 2019 Fifth Internet Edition (Corrected TOC) 19.01 January 17, 2019 Fifth Internet Edition. 17.10 October 19, 2017 Fourth Internet Edition. 16.07 July 28, 2016 Third Internet Edition. 13.07 July 6, 2013 Second Internet Edition. 09.12 December 14, 2009 First Internet Edition. Table of Contents Introduction....................................................................................................xvi Why Use the Command Line?......................................................................................xvi