The Numerics of Phase Retrieval
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Introduction to Phasing Crystallography ISSN 0907-4449
research papers Acta Crystallographica Section D Biological Introduction to phasing Crystallography ISSN 0907-4449 Garry L. Taylor When collecting X-ray diffraction data from a crystal, we Received 30 August 2009 measure the intensities of the diffracted waves scattered from Accepted 22 February 2010 a series of planes that we can imagine slicing through the Centre for Biomolecular Sciences, University of St Andrews, St Andrews, Fife KY16 9ST, crystal in all directions. From these intensities we derive the Scotland amplitudes of the scattered waves, but in the experiment we lose the phase information; that is, how we offset these waves when we add them together to reconstruct an image of our Correspondence e-mail: [email protected] molecule. This is generally known as the ‘phase problem’. We can only derive the phases from some knowledge of the molecular structure. In small-molecule crystallography, some basic assumptions about atomicity give rise to relationships between the amplitudes from which phase information can be extracted. In protein crystallography, these ab initio methods can only be used in the rare cases in which there are data to at least 1.2 A˚ resolution. For the majority of cases in protein crystallography phases are derived either by using the atomic coordinates of a structurally similar protein (molecular replacement) or by finding the positions of heavy atoms that are intrinsic to the protein or that have been added (methods such as MIR, MIRAS, SIR, SIRAS, MAD, SAD or com- binations of these). The pioneering work of Perutz, Kendrew, Blow, Crick and others developed the methods of isomor- phous replacement: adding electron-dense atoms to the protein without disturbing the protein structure. -

System Design and Verification of the Precession Electron Diffraction Technique
NORTHWESTERN UNIVERSITY System Design and Verification of the Precession Electron Diffraction Technique A DISSERTATION SUBMITTED TO THE GRADUATE SCHOOL IN PARTIAL FULFILLMENT OF THE REQUIREMENTS for the degree DOCTOR OF PHILOSOPHY Field of Materials Science and Engineering By Christopher Su-Yan Own EVANSTON, ILLINOIS First published on the WWW 01, August 2005 Build 05.12.07. PDF available for download at: http://www.numis.northwestern.edu/Research/Current/precession.shtml c Copyright by Christopher Su-Yan Own 2005 All Rights Reserved ii ABSTRACT System Design and Verification of the Precession Electron Diffraction Technique Christopher Su-Yan Own Bulk structural crystallography is generally a two-part process wherein a rough starting structure model is first derived, then later refined to give an accurate model of the structure. The critical step is the deter- mination of the initial model. As materials problems decrease in length scale, the electron microscope has proven to be a versatile and effective tool for studying many problems. However, study of complex bulk structures by electron diffraction has been hindered by the problem of dynamical diffraction. This phenomenon makes bulk electron diffraction very sensitive to specimen thickness, and expensive equip- ment such as aberration-corrected scanning transmission microscopes or elaborate methodology such as high resolution imaging combined with diffraction and simulation are often required to generate good starting structures. The precession electron diffraction technique (PED), which has the ability to significantly reduce dynamical effects in diffraction patterns, has shown promise as being a “philosopher’s stone” for bulk electron diffraction. However, a comprehensive understanding of its abilities and limitations is necessary before it can be put into widespread use as a standalone technique. -

Optical Ptychographic Phase Tomography
University College London Final year project Optical Ptychographic Phase Tomography Supervisors: Author: Prof. Ian Robinson Qiaoen Luo Dr. Fucai Zhang March 20, 2013 Abstract The possibility of combining ptychographic iterative phase retrieval and computerised tomography using optical waves was investigated in this report. The theoretical background and historic developments of ptychographic phase retrieval was reviewed in the first part of the report. A simple review of the principles behind computerised tomography was given with 2D and 3D simulations in the following chapters. The sample used in the experiment is a glass tube with its outer wall glued with glass microspheres. The tube has a diameter of approx- imately 1 mm and the microspheres have a diameter of 30 µm. The experiment demonstrated the successful recovery of features of the sam- ple with limited resolution. The results could be improved in future attempts. In addition, phase unwrapping techniques were compared and evaluated in the report. This technique could retrieve the three dimensional refractive index distribution of an optical component (ideally a cylindrical object) such as an opitcal fibre. As it is relatively an inexpensive and readily available set-up compared to X-ray phase tomography, the technique can have a promising future for application at large scale. Contents List of Figures i 1 Introduction 1 2 Theory 3 2.1 Phase Retrieval . .3 2.1.1 Phase Problem . .3 2.1.2 The Importance of Phase . .5 2.1.3 Phase Retrieval Iterative Algorithms . .7 2.2 Ptychography . .9 2.2.1 Ptychography Principle . .9 2.2.2 Ptychographic Iterative Engine . -

X-Ray Crystallography
X-ray Crystallography Prof. Leonardo Scapozza Pharmceutical Biochemistry School of Pharmaceutical Sciences University of Geneva, University of Lausanne E-mail: [email protected] Aim • Introduce the students to X-ray crystallography • Give the students the tools to “evaluate” a X-ray structure based scientific paper 1 Outline • The History of X-ray • The Principle of X-ray • The Steps towards the 3D structure – Crystallization – X-ray diffraction and data collection – From Pattern of Diffraction to Electron Density – X-ray structure quality assessment An extract of a structure paper 2.1. Crystallization • The hTK1 was cloned as N-terminal thrombin-cleavable His6–tagged fusion protein missing 14 amino acids of the N-terminus and 40 amino acids of the C–terminus of the wild type hTK1 sequence of 234 amino acids (this construct is further on called hTK1). The purified hTK1, consisting of residues 15-194 of the wild type sequence plus an N–terminal extension of 15 residues containing a His6–tag, was eluted from gel filtration column at a concentration of approximate 7 mg/ml with a buffer containing 5 mM Tris at pH 7.2, 10 mM NaCl and 10 mM DTT. For protein crystallization we used the hanging drop method at 23°C. Initial conditions for crystallization were found using Crystal screen Cryo no. 40 (Hampton Research). The protein solution was mixed in a 1:1 ratio with crystallization buffer (0.095 mM tri–sodium citrate pH 5.5, 12% PEG 4000, 10% isopropanol) to set up drops of 6 μl. The reservoir contained 500 μl of crystallization buffer. -
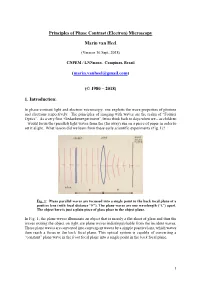
Principles of the Phase Contrast (Electron) Microscopy
Principles of Phase Contrast (Electron) Microscopy Marin van Heel (Version 16 Sept. 2018) CNPEM / LNNnano, Campinas, Brazil ([email protected]) (© 1980 – 2018) 1. Introduction: In phase-contrast light and electron microscopy, one exploits the wave properties of photons and electrons respectively. The principles of imaging with waves are the realm of “Fourier Optics”. As a very first “Gedankenexperiment”, let us think back to days when we – as children – would focus the (parallel) light waves from the (far away) sun on a piece of paper in order to set it alight. What lesson did we learn from these early scientific experiments (Fig. 1)? Fig. 1: Plane parallel waves are focussed into a single point in the back focal plane of a positive lens (with focal distance “F”). The plane waves are one wavelength (“λ”) apart. The object here is just a plain piece of glass place in the object plane. In Fig. 1, the plane waves illuminate an object that is merely a flat sheet of glass and thus the waves exiting the object on right are plane waves indistinguishable from the incident waves. These plane waves are converted into convergent waves by a simple positive lens, which waves then reach a focus in the back focal plane. This optical system is capable of converting a “constant” plane wave in the front focal plane into a single point in the back focal plane. 1 Fig. 2: A single point scatterer in the object plane leads to secondary (“scattered”) concentric waves emerging from that point in the object. Since the object is placed in the front focal plane, these scattered or “diffracted” secondary waves become plane waves hitting the back focal plane of the system. -

The Geometry of the Phase Retrieval Problem Charles L
The Geometry of the Phase Retrieval Problem Charles L. Epstein The Geometry of the Phase Retrieval Problem Introduction Operator Splitting Methods in Data Analysis Workshop Discrete Problem Torus Geometry Reconstruction Charles L. Epstein Algorithms Numerical Examples CCM at the Flatiron Institute University of Pennsylvania Other Conditions History of CDI March 20, 2019 Bibliography Acknowledgment The Geometry of the Phase Retrieval Problem Charles L. Epstein I want to thank Christian and Patrick for inviting me to speak. Introduction What I will discuss today is somewhat unconventional, ongoing Discrete Problem work, at the intersection of pure mathematics, numerical analysis Torus Geometry and mathematical physics. Reconstruction Algorithms This work was done jointly with Alex Barnett, Leslie Greengard, Numerical and Jeremy Magland and supported by the Centers for Examples Computational Biology and Mathematics at the Flatiron Institute Other Conditions of the Simons Foundation, New York, NY. History of CDI Bibliography Outline The Geometry of the Phase Retrieval Problem 1 Introduction Charles L. Epstein 2 The Discrete Phase Retrieval Problem Introduction 3 Geometry of the Torus Discrete Problem Torus Geometry 4 Reconstruction Algorithms Reconstruction Algorithms 5 Numerical Examples in Phase Retrieval Numerical Examples 6 Other Auxiliary Conditions Other Conditions History of CDI 7 Short History of CDI Bibliography 8 Bibliography High Resolution Imaging The Geometry of the Phase Retrieval Problem Charles L. Epstein Introduction Today I will speak about inverse problems that arise in Coherent Discrete Problem Diffraction Imaging. This is a technique that uses very high Torus Geometry energy, monochromatic light, either electrons or x-rays, to form Reconstruction high resolution images of animate and inanimate materials. -
Phase Problem in X-Ray Crystallography, and Its Solution Reciprocal Directions and Spacings from the Real Lattice
Phase Problem in X-ray Secondary article Crystallography, and Its Article Contents . The Phase Problem in X-ray Crystallography Solution . Patterson Methods . Direct Methods Kevin Cowtan, University of York, UK . Multiple Isomorphous Replacement . Multiwavelength Anomalous Dispersion (MAD) X-ray crystallography can provide detailed information about the structure of biological . Molecular Replacement molecules if the ‘phase problem’ can be solved for the molecule under study. The . Phase Improvement phase problem arises because it is only possible to measure the amplitude of diffraction . Summary spots: information on the phase of the diffracted radiation is missing. Techniques are available to reconstruct this information. The Phase Problem in X-ray called the unit cell. It is convenient to define crystal axes a, b Crystallography and c defining the unit cell in three dimensions. Scattering along directions reflecting the lattice repeat will be X-ray diffraction provides one of the most important tools reinforced by every repeat of the unit cell, and will be for examining the three-dimensional (3D) structure of strong; scattering along all other directions will be weak. biological macromolecules. The physics of diffraction As a result, the full diffraction pattern of the crystal is a requires that in order to resolve features of atomic pattern of spots, forming a three-dimensional lattice with structure it is necessary to employ radiation with a wavelength of the order of atomic spacing or smaller. X- rays have suitable wavelength, and interact with the Scattered waves are electrons of the atoms. However, the interaction between out of phase X-rays and electrons is weak, and such energetic radiation causes ionization of the constituent atoms of the molecule, damaging the molecule under study. -

Aspects of Phase Retrieval in X-Ray Crystallography
Aspects of Phase Retrieval in X-ray Crystallography Romain Arnal A thesis presented for the degree of Doctor of Philosophy in Electrical and Computer Engineering at the University of Canterbury, Christchurch, New Zealand. June 2019 Deputy Vice-Chancellor’s Office Postgraduate Office Co-Authorship Form This form is to accompany the submission of any thesis that contains research reported in co- authored work that has been published, accepted for publication, or submitted for publication. A copy of this form should be included for each co-authored work that is included in the thesis. Completed forms should be included at the front (after the thesis abstract) of each copy of the thesis submitted for examination and library deposit. Please indicate the chapter/section/pages of this thesis that are extracted from co-authored work and provide details of the publication or submission from the extract comes: Chapter 2 describes work by the candidate that is reported in “Millane and Arnal, Uniqueness of the macromolecular crystallographic phase problem, Acta Cryst., A71, 592-598, 2015.” Please detail the nature and extent (%) of contribution by the candidate: This publication describes joint work by the candidate and Millane. The theory was derived jointly by the candidate and Millane. The simulations, the required software development, and presentation of the results were conducted by the candidate. Writing was a joint effort. Certification by Co-authors: If there is more than one co-author then a single co-author can sign on behalf of all The -

Measurements of Phase Changes in Crystals Using Ptychographic X-Ray
Measurements of phase changes in crystals using Ptychographic X-ray imaging Maria Civita October 2016 Declaration I, Maria Civita, confirm that the work presented in this Thesis is my own. Where information has been derived from other sources, I confirm that this has been indicated in the Thesis. Abstract In a typical X-ray diffraction experiment we are only able to directly retrieve part of the information which characterizes the propagating wave transmitted through the sample: while its intensity can be recorded with the use of appropriate detectors, the phase is lost. Because the phase term which is accumulated when an X-ray beam is transmitted through a slab of material is due to refraction [1, 2], and hence it contains relevant information about the structure of the sample, finding a solution to the “phase problem” has been a central theme over the years. Many authors successfully developed a number of techniques which were able to solve the problem in the past [3, 4, 5, 6], but the interest around this subject also continues nowadays [7, 8]. With this Thesis work, we aim to give a valid contribution to the phase problem solution by illustrating the first application of the ptychographic imaging technique [9, 10, 11, 12, 13, 14] to measure the effect of Bragg diffraction on the transmitted phase, collected in the forward direction. In particular, we will discuss the experimental methodology which allowed to detect the small phase variations in the transmitted wave when changing the X-ray’s incidence angle around the Bragg condition. Furthermore, we will provide an overview of the theoretical frameworks which can allow to interpret the experimental results obtained. -

This Is a Repository Copy of Ptychography. White Rose
This is a repository copy of Ptychography. White Rose Research Online URL for this paper: http://eprints.whiterose.ac.uk/127795/ Version: Accepted Version Book Section: Rodenburg, J.M. orcid.org/0000-0002-1059-8179 and Maiden, A.M. (2019) Ptychography. In: Hawkes, P.W. and Spence, J.C.H., (eds.) Springer Handbook of Microscopy. Springer Handbooks . Springer . ISBN 9783030000684 https://doi.org/10.1007/978-3-030-00069-1_17 This is a post-peer-review, pre-copyedit version of a chapter published in Hawkes P.W., Spence J.C.H. (eds) Springer Handbook of Microscopy. The final authenticated version is available online at: https://doi.org/10.1007/978-3-030-00069-1_17. Reuse Items deposited in White Rose Research Online are protected by copyright, with all rights reserved unless indicated otherwise. They may be downloaded and/or printed for private study, or other acts as permitted by national copyright laws. The publisher or other rights holders may allow further reproduction and re-use of the full text version. This is indicated by the licence information on the White Rose Research Online record for the item. Takedown If you consider content in White Rose Research Online to be in breach of UK law, please notify us by emailing [email protected] including the URL of the record and the reason for the withdrawal request. [email protected] https://eprints.whiterose.ac.uk/ Ptychography John Rodenburg and Andy Maiden Abstract: Ptychography is a computational imaging technique. A detector records an extensive data set consisting of many inference patterns obtained as an object is displaced to various positions relative to an illumination field. -

Iterative Phase Retrieval in Coherent Diffractive Imaging: Practical Issues
Iterative phase retrieval in coherent diffractive imaging: practical issues Tatiana Latychevskaia, [email protected] ABSTRACT In this work, issues in phase retrieval in the coherent diffractive imaging (CDI) technique, from discussion on parameters for setting up a CDI experiment to evaluation of the goodness of the final reconstruction, are discussed. The distribution of objects under study by CDI often cannot be cross- validated by another imaging technique. It is therefore important to make sure that the developed CDI procedure delivers an artifact-free object reconstruction. Critical issues that can lead to artifacts are presented and recipes on how to avoid them are provided. Contents Iterative phase retrieval in coherent diffractive imaging: practical issues ............................................. 1 1. Introduction ......................................................................................................................................... 3 2. Basics of CDI experiment ..................................................................................................................... 3 2.1. Diffraction pattern formation ...................................................................................................... 3 2.2 Oversampling ................................................................................................................................. 6 2.3 Iterative phase-retrieval algorithms .............................................................................................. 7 2.3.1 -

Low-Rank Fourier Ptychography
LOW RANK FOURIER PTYCHOGRAPHY Zhengyu Chen, Gauri Jagatap, Seyedehsara Nayer, Chinmay Hegde, Namrata Vaswani Iowa State University ABSTRACT reconstruction problem is nascent, and several important questions remain unanswered. Rigorous guarantees of correctness of the meth- In this paper, we introduce a principled algorithmic approach for ods proposed in [8, 10] are not yet available. More worrisome is the Fourier ptychographic imaging of dynamic, time-varying targets. To issue of sample complexity of image reconstruction, since a basic the best of our knowledge, this setting has not been explicitly ad- requirement in all existing methods is that the number of measure- dressed in the ptychography literature. We argue that such a setting ments must exceed the resolution of the image. However, this re- is very natural, and that our methods provide an important first step quirement can be particularly challenging when imaging a dynamic towards helping reduce the sample complexity (and hence acquisi- scene involving a moving target; for a video sequence with q images tion time) of imaging dynamic scenes to managaeble levels. With each with resolution n, without using any structural prior assump- significantly reduced acquisition times per image, it is conceivable tions, the number of observations must be at least Ω(nq), which can that dynamic ptychographic imaging of fast changing scenes indeeed quickly become prohibitive. becomes practical in the near future. Index Terms— Phase retrieval, ptychography, low rank 1.2. Our Contributions 1. INTRODUCTION In this paper, we introduce a principled algorithmic approach for Fourier ptychographic imaging of dynamic, time-varying targets. To 1.1. Motivation the best of our knowledge, this setting has not been explicitly ad- dressed in the ptychography literature.