On the Numerical Performance of Derivative-Free Optimization Methods Based on Finite-Difference Approximations
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

University of California, San Diego
UNIVERSITY OF CALIFORNIA, SAN DIEGO Computational Methods for Parameter Estimation in Nonlinear Models A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Physics with a Specialization in Computational Physics by Bryan Andrew Toth Committee in charge: Professor Henry D. I. Abarbanel, Chair Professor Philip Gill Professor Julius Kuti Professor Gabriel Silva Professor Frank Wuerthwein 2011 Copyright Bryan Andrew Toth, 2011 All rights reserved. The dissertation of Bryan Andrew Toth is approved, and it is acceptable in quality and form for publication on microfilm and electronically: Chair University of California, San Diego 2011 iii DEDICATION To my grandparents, August and Virginia Toth and Willem and Jane Keur, who helped put me on a lifelong path of learning. iv EPIGRAPH An Expert: One who knows more and more about less and less, until eventually he knows everything about nothing. |Source Unknown v TABLE OF CONTENTS Signature Page . iii Dedication . iv Epigraph . v Table of Contents . vi List of Figures . ix List of Tables . x Acknowledgements . xi Vita and Publications . xii Abstract of the Dissertation . xiii Chapter 1 Introduction . 1 1.1 Dynamical Systems . 1 1.1.1 Linear and Nonlinear Dynamics . 2 1.1.2 Chaos . 4 1.1.3 Synchronization . 6 1.2 Parameter Estimation . 8 1.2.1 Kalman Filters . 8 1.2.2 Variational Methods . 9 1.2.3 Parameter Estimation in Nonlinear Systems . 9 1.3 Dissertation Preview . 10 Chapter 2 Dynamical State and Parameter Estimation . 11 2.1 Introduction . 11 2.2 DSPE Overview . 11 2.3 Formulation . 12 2.3.1 Least Squares Minimization . -

Click to Edit Master Title Style
Click to edit Master title style MINLP with Combined Interior Point and Active Set Methods Jose L. Mojica Adam D. Lewis John D. Hedengren Brigham Young University INFORM 2013, Minneapolis, MN Presentation Overview NLP Benchmarking Hock-Schittkowski Dynamic optimization Biological models Combining Interior Point and Active Set MINLP Benchmarking MacMINLP MINLP Model Predictive Control Chiller Thermal Energy Storage Unmanned Aerial Systems Future Developments Oct 9, 2013 APMonitor.com APOPT.com Brigham Young University Overview of Benchmark Testing NLP Benchmark Testing 1 1 2 3 3 min J (x, y,u) APOPT , BPOPT , IPOPT , SNOPT , MINOS x Problem characteristics: s.t. 0 f , x, y,u t Hock Schittkowski, Dynamic Opt, SBML 0 g(x, y,u) Nonlinear Programming (NLP) Differential Algebraic Equations (DAEs) 0 h(x, y,u) n m APMonitor Modeling Language x, y u MINLP Benchmark Testing min J (x, y,u, z) 1 1 2 APOPT , BPOPT , BONMIN x s.t. 0 f , x, y,u, z Problem characteristics: t MacMINLP, Industrial Test Set 0 g(x, y,u, z) Mixed Integer Nonlinear Programming (MINLP) 0 h(x, y,u, z) Mixed Integer Differential Algebraic Equations (MIDAEs) x, y n u m z m APMonitor & AMPL Modeling Language 1–APS, LLC 2–EPL, 3–SBS, Inc. Oct 9, 2013 APMonitor.com APOPT.com Brigham Young University NLP Benchmark – Summary (494) 100 90 80 APOPT+BPOPT APOPT 70 1.0 BPOPT 1.0 60 IPOPT 3.10 IPOPT 50 2.3 SNOPT Percentage (%) 6.1 40 Benchmark Results MINOS 494 Problems 5.5 30 20 10 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 5 Not worse than 2 times slower than -

Specifying “Logical” Conditions in AMPL Optimization Models
Specifying “Logical” Conditions in AMPL Optimization Models Robert Fourer AMPL Optimization www.ampl.com — 773-336-AMPL INFORMS Annual Meeting Phoenix, Arizona — 14-17 October 2012 Session SA15, Software Demonstrations Robert Fourer, Logical Conditions in AMPL INFORMS Annual Meeting — 14-17 Oct 2012 — Session SA15, Software Demonstrations 1 New and Forthcoming Developments in the AMPL Modeling Language and System Optimization modelers are often stymied by the complications of converting problem logic into algebraic constraints suitable for solvers. The AMPL modeling language thus allows various logical conditions to be described directly. Additionally a new interface to the ILOG CP solver handles logic in a natural way not requiring conventional transformations. Robert Fourer, Logical Conditions in AMPL INFORMS Annual Meeting — 14-17 Oct 2012 — Session SA15, Software Demonstrations 2 AMPL News Free AMPL book chapters AMPL for Courses Extended function library Extended support for “logical” conditions AMPL driver for CPLEX Opt Studio “Concert” C++ interface Support for ILOG CP constraint programming solver Support for “logical” constraints in CPLEX INFORMS Impact Prize to . Originators of AIMMS, AMPL, GAMS, LINDO, MPL Awards presented Sunday 8:30-9:45, Conv Ctr West 101 Doors close 8:45! Robert Fourer, Logical Conditions in AMPL INFORMS Annual Meeting — 14-17 Oct 2012 — Session SA15, Software Demonstrations 3 AMPL Book Chapters now free for download www.ampl.com/BOOK/download.html Bound copies remain available purchase from usual -
Standard Price List
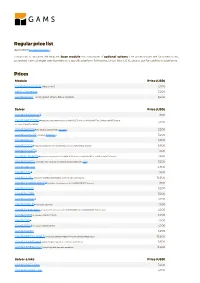
Regular price list April 2021 (Download PDF ) This price list includes the required base module and a number of optional solvers. The prices shown are for unrestricted, perpetual named single user licenses on a specific platform (Windows, Linux, Mac OS X), please ask for additional platforms. Prices Module Price (USD) GAMS/Base Module (required) 3,200 MIRO Connector 3,200 GAMS/Secure - encrypted Work Files Option 3,200 Solver Price (USD) GAMS/ALPHAECP 1 1,600 GAMS/ANTIGONE 1 (requires the presence of a GAMS/CPLEX and a GAMS/SNOPT or GAMS/CONOPT license, 3,200 includes GAMS/GLOMIQO) GAMS/BARON 1 (for details please follow this link ) 3,200 GAMS/CONOPT (includes CONOPT 4 ) 3,200 GAMS/CPLEX 9,600 GAMS/DECIS 1 (requires presence of a GAMS/CPLEX or a GAMS/MINOS license) 9,600 GAMS/DICOPT 1 1,600 GAMS/GLOMIQO 1 (requires presence of a GAMS/CPLEX and a GAMS/SNOPT or GAMS/CONOPT license) 1,600 GAMS/IPOPTH (includes HSL-routines, for details please follow this link ) 3,200 GAMS/KNITRO 4,800 GAMS/LGO 2 1,600 GAMS/LINDO (includes GAMS/LINDOGLOBAL with no size restrictions) 12,800 GAMS/LINDOGLOBAL 2 (requires the presence of a GAMS/CONOPT license) 1,600 GAMS/MINOS 3,200 GAMS/MOSEK 3,200 GAMS/MPSGE 1 3,200 GAMS/MSNLP 1 (includes LSGRG2) 1,600 GAMS/ODHeuristic (requires the presence of a GAMS/CPLEX or a GAMS/CPLEX-link license) 3,200 GAMS/PATH (includes GAMS/PATHNLP) 3,200 GAMS/SBB 1 1,600 GAMS/SCIP 1 (includes GAMS/SOPLEX) 3,200 GAMS/SNOPT 3,200 GAMS/XPRESS-MINLP (includes GAMS/XPRESS-MIP and GAMS/XPRESS-NLP) 12,800 GAMS/XPRESS-MIP (everything but general nonlinear equations) 9,600 GAMS/XPRESS-NLP (everything but discrete variables) 6,400 Solver-Links Price (USD) GAMS/CPLEX Link 3,200 GAMS/GUROBI Link 3,200 Solver-Links Price (USD) GAMS/MOSEK Link 1,600 GAMS/XPRESS Link 3,200 General information The GAMS Base Module includes the GAMS Language Compiler, GAMS-APIs, and many utilities . -

Julia: a Modern Language for Modern ML
Julia: A modern language for modern ML Dr. Viral Shah and Dr. Simon Byrne www.juliacomputing.com What we do: Modernize Technical Computing Today’s technical computing landscape: • Develop new learning algorithms • Run them in parallel on large datasets • Leverage accelerators like GPUs, Xeon Phis • Embed into intelligent products “Business as usual” will simply not do! General Micro-benchmarks: Julia performs almost as fast as C • 10X faster than Python • 100X faster than R & MATLAB Performance benchmark relative to C. A value of 1 means as fast as C. Lower values are better. A real application: Gillespie simulations in systems biology 745x faster than R • Gillespie simulations are used in the field of drug discovery. • Also used for simulations of epidemiological models to study disease propagation • Julia package (Gillespie.jl) is the state of the art in Gillespie simulations • https://github.com/openjournals/joss- papers/blob/master/joss.00042/10.21105.joss.00042.pdf Implementation Time per simulation (ms) R (GillespieSSA) 894.25 R (handcoded) 1087.94 Rcpp (handcoded) 1.31 Julia (Gillespie.jl) 3.99 Julia (Gillespie.jl, passing object) 1.78 Julia (handcoded) 1.2 Those who convert ideas to products fastest will win Computer Quants develop Scientists prepare algorithms The last 25 years for production (Python, R, SAS, DEPLOY (C++, C#, Java) Matlab) Quants and Computer Compress the Scientists DEPLOY innovation cycle collaborate on one platform - JULIA with Julia Julia offers competitive advantages to its users Julia is poised to become one of the Thank you for Julia. Yo u ' v e k i n d l ed leading tools deployed by developers serious excitement. -

Treball (1.484Mb)
Treball Final de Màster MÀSTER EN ENGINYERIA INFORMÀTICA Escola Politècnica Superior Universitat de Lleida Mòdul d’Optimització per a Recursos del Transport Adrià Vall-llaura Salas Tutors: Antonio Llubes, Josep Lluís Lérida Data: Juny 2017 Pròleg Aquest projecte s’ha desenvolupat per donar solució a un problema de l’ordre del dia d’una empresa de transports. Es basa en el disseny i implementació d’un model matemàtic que ha de permetre optimitzar i automatitzar el sistema de planificació de viatges de l’empresa. Per tal de poder implementar l’algoritme s’han hagut de crear diversos mòduls que extreuen les dades del sistema ERP, les tracten, les envien a un servei web (REST) i aquest retorna un emparellament òptim entre els vehicles de l’empresa i les ordres dels clients. La primera fase del projecte, la teòrica, ha estat llarga en comparació amb les altres. En aquesta fase s’ha estudiat l’estat de l’art en la matèria i s’han repassat molts dels models més importants relacionats amb el transport per comprendre’n les seves particularitats. Amb els conceptes ben estudiats, s’ha procedit a desenvolupar un nou model matemàtic adaptat a les necessitats de la lògica de negoci de l’empresa de transports objecte d’aquest treball. Posteriorment s’ha passat a la fase d’implementació dels mòduls. En aquesta fase m’he trobat amb diferents limitacions tecnològiques degudes a l’antiguitat de l’ERP i a l’ús del sistema operatiu Windows. També han sorgit diferents problemes de rendiment que m’han fet redissenyar l’extracció de dades de l’ERP, el càlcul de distàncies i el mòdul d’optimització. -

GEKKO Documentation Release 1.0.1
GEKKO Documentation Release 1.0.1 Logan Beal, John Hedengren Aug 31, 2021 Contents 1 Overview 1 2 Installation 3 3 Project Support 5 4 Citing GEKKO 7 5 Contents 9 6 Overview of GEKKO 89 Index 91 i ii CHAPTER 1 Overview GEKKO is a Python package for machine learning and optimization of mixed-integer and differential algebraic equa- tions. It is coupled with large-scale solvers for linear, quadratic, nonlinear, and mixed integer programming (LP, QP, NLP, MILP, MINLP). Modes of operation include parameter regression, data reconciliation, real-time optimization, dynamic simulation, and nonlinear predictive control. GEKKO is an object-oriented Python library to facilitate local execution of APMonitor. More of the backend details are available at What does GEKKO do? and in the GEKKO Journal Article. Example applications are available to get started with GEKKO. 1 GEKKO Documentation, Release 1.0.1 2 Chapter 1. Overview CHAPTER 2 Installation A pip package is available: pip install gekko Use the —-user option to install if there is a permission error because Python is installed for all users and the account lacks administrative priviledge. The most recent version is 0.2. You can upgrade from the command line with the upgrade flag: pip install--upgrade gekko Another method is to install in a Jupyter notebook with !pip install gekko or with Python code, although this is not the preferred method: try: from pip import main as pipmain except: from pip._internal import main as pipmain pipmain(['install','gekko']) 3 GEKKO Documentation, Release 1.0.1 4 Chapter 2. Installation CHAPTER 3 Project Support There are GEKKO tutorials and documentation in: • GitHub Repository (examples folder) • Dynamic Optimization Course • APMonitor Documentation • GEKKO Documentation • 18 Example Applications with Videos For project specific help, search in the GEKKO topic tags on StackOverflow. -

Largest Small N-Polygons: Numerical Results and Conjectured Optima
Largest Small n-Polygons: Numerical Results and Conjectured Optima János D. Pintér Department of Industrial and Systems Engineering Lehigh University, Bethlehem, PA, USA [email protected] Abstract LSP(n), the largest small polygon with n vertices, is defined as the polygon of unit diameter that has maximal area A(n). Finding the configuration LSP(n) and the corresponding A(n) for even values n 6 is a long-standing challenge that leads to an interesting class of nonlinear optimization problems. We present numerical solution estimates for all even values 6 n 80, using the AMPL model development environment with the LGO nonlinear solver engine option. Our results compare favorably to the results obtained by other researchers who solved the problem using exact approaches (for 6 n 16), or general purpose numerical optimization software (for selected values from the range 6 n 100) using various local nonlinear solvers. Based on the results obtained, we also provide a regression model based estimate of the optimal area sequence {A(n)} for n 6. Key words Largest Small Polygons Mathematical Model Analytical and Numerical Solution Approaches AMPL Modeling Environment LGO Solver Suite For Nonlinear Optimization AMPL-LGO Numerical Results Comparison to Earlier Results Regression Model Based Optimum Estimates 1 Introduction The diameter of a (convex planar) polygon is defined as the maximal distance among the distances measured between all vertex pairs. In other words, the diameter of the polygon is the length of its longest diagonal. The largest small polygon with n vertices is the polygon of unit diameter that has maximal area. For any given integer n 3, we will refer to this polygon as LSP(n) with area A(n). -

AMPL Academic Price List These Prices Apply to Purchases by Degree-Awarding Institutions for Use in Noncommercial Teaching and Research Activities
AMPL Optimization Inc. 211 Hope Street #339 Mountain View, CA 94041, U.S.A. [email protected] — www.ampl.com +1 773-336-AMPL (-2675) AMPL Academic Price List These prices apply to purchases by degree-awarding institutions for use in noncommercial teaching and research activities. Products covered by academic prices are full-featured and have no arbitrary limits on problem size. Single Floating AMPL $400 $600 Linear/quadratic solvers: CPLEX free 1-year licenses available: see below Gurobi free 1-year licenses available: see below Xpress free 1-year licenses available: see below Nonlinear solvers: Artelys Knitro $400 $600 CONOPT $400 $600 LOQO $300 $450 MINOS $300 $450 SNOPT $320 $480 Alternative solvers: BARON $400 $600 LGO $200 $300 LINDO Global $700 $950 . Basic $400 $600 (limited to 3200 nonlinear variables) Web-based collaborative environment: QuanDec $1400 $2100 AMPL prices are for the AMPL modeling language and system, including the AMPL command-line and IDE development tools and the AMPL API programming libraries. To make use of AMPL it is necessary to also obtain at least one solver having an AMPL interface. Solvers may be obtained from us or from another source. As listed above, we offer many popular solvers for direct purchase; refer to www.ampl.com/products/solvers/solvers-we-sell/ to learn more, including problem types supported and methods used. Our prices for these solvers apply to the versions that incorporate an AMPL interface; a previously or concurrently purchased copy of the AMPL software is needed to use these versions. Programming libraries and other forms of these solvers are not included. -

Users Guide for Snadiopt: a Package Adding Automatic Differentiation to Snopt∗
USERS GUIDE FOR SNADIOPT: A PACKAGE ADDING AUTOMATIC DIFFERENTIATION TO SNOPT∗ E. Michael GERTZ Mathematics and Computer Science Division Argonne National Laboratory Argonne, Illinois 60439 Philip E. GILL and Julia MUETHERIG Department of Mathematics University of California, San Diego La Jolla, California 92093-0112 January 2001 Abstract SnadiOpt is a package that supports the use of the automatic differentiation package ADIFOR with the optimization package Snopt. Snopt is a general-purpose system for solving optimization problems with many variables and constraints. It minimizes a linear or nonlinear function subject to bounds on the variables and sparse linear or nonlinear constraints. It is suitable for large-scale linear and quadratic programming and for linearly constrained optimization, as well as for general nonlinear programs. The method used by Snopt requires the first derivatives of the objective and con- straint functions to be available. The SnadiOpt package allows users to avoid the time- consuming and error-prone process of evaluating and coding these derivatives. Given Fortran code for evaluating only the values of the objective and constraints, SnadiOpt automatically generates the code for evaluating the derivatives and builds the relevant Snopt input files and sparse data structures. Keywords: Large-scale nonlinear programming, constrained optimization, SQP methods, automatic differentiation, Fortran software. [email protected] [email protected] [email protected] http://www.mcs.anl.gov/ gertz/ http://www.scicomp.ucsd.edu/ peg/ http://www.scicomp.ucsd.edu/ julia/ ∼ ∼ ∼ ∗Partially supported by National Science Foundation grant CCR-95-27151. Contents 1. Introduction 3 1.1 Problem Types . 3 1.2 Why Automatic Differentiation? . 3 1.3 ADIFOR ...................................... -

MP-Opt-Model User's Manual, Version
MP-Opt-Model User's Manual Version 2.1 Ray D. Zimmerman August 25, 2020 © 2020 Power Systems Engineering Research Center (PSerc) All Rights Reserved Contents 1 Introduction6 1.1 Background................................6 1.2 License and Terms of Use........................7 1.3 Citing MP-Opt-Model..........................8 1.4 MP-Opt-Model Development.......................8 2 Getting Started9 2.1 System Requirements...........................9 2.2 Installation................................9 2.3 Sample Usage............................... 10 2.4 Documentation.............................. 14 3 MP-Opt-Model { Overview 15 4 Solver Interface Functions 16 4.1 LP/QP Solvers { qps master ...................... 16 4.1.1 QP Example............................ 19 4.2 MILP/MIQP Solvers { miqps master .................. 20 4.2.1 MILP Example.......................... 22 4.3 NLP Solvers { nlps master ....................... 22 4.3.1 NLP Example 1.......................... 25 4.3.2 NLP Example 2.......................... 26 4.4 Nonlinear Equation Solvers { nleqs master .............. 29 4.4.1 NLEQ Example 1......................... 31 4.4.2 NLEQ Example 2......................... 34 5 Optimization Model Class { opt model 38 5.1 Adding Variables............................. 38 5.1.1 Variable Subsets......................... 39 5.2 Adding Constraints............................ 40 5.2.1 Linear Constraints........................ 40 5.2.2 General Nonlinear Constraints.................. 41 5.3 Adding Costs............................... 42 5.3.1 Quadratic -

The Optimization Module User's Guide
Optimization Module User’s Guide Optimization Module User’s Guide © 1998–2018 COMSOL Protected by patents listed on www.comsol.com/patents, and U.S. Patents 7,519,518; 7,596,474; 7,623,991; 8,457,932; 8,954,302; 9,098,106; 9,146,652; 9,323,503; 9,372,673; and 9,454,625. Patents pending. This Documentation and the Programs described herein are furnished under the COMSOL Software License Agreement (www.comsol.com/comsol-license-agreement) and may be used or copied only under the terms of the license agreement. COMSOL, the COMSOL logo, COMSOL Multiphysics, COMSOL Desktop, COMSOL Server, and LiveLink are either registered trademarks or trademarks of COMSOL AB. All other trademarks are the property of their respective owners, and COMSOL AB and its subsidiaries and products are not affiliated with, endorsed by, sponsored by, or supported by those trademark owners. For a list of such trademark owners, see www.comsol.com/trademarks. Version: COMSOL 5.4 Contact Information Visit the Contact COMSOL page at www.comsol.com/contact to submit general inquiries, contact Technical Support, or search for an address and phone number. You can also visit the Worldwide Sales Offices page at www.comsol.com/contact/offices for address and contact information. If you need to contact Support, an online request form is located at the COMSOL Access page at www.comsol.com/support/case. Other useful links include: • Support Center: www.comsol.com/support • Product Download: www.comsol.com/product-download • Product Updates: www.comsol.com/support/updates • COMSOL Blog: www.comsol.com/blogs • Discussion Forum: www.comsol.com/community • Events: www.comsol.com/events • COMSOL Video Gallery: www.comsol.com/video • Support Knowledge Base: www.comsol.com/support/knowledgebase Part number: CM021701 Contents Chapter 1: Introduction Optimization Module Overview 8 What Can the Optimization Module Do?.