DOCSLIB.ORG

13.3 Digital Elliptic Filter Design

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
13.3 Digital Elliptic Filter Design CHAPTER 13 IIR FILTER DESIGN 13.3 Digital Elliptic Filter Design This document carries out design of a discrete-time elliptic lowpass filter. The user specifies the following parameters: passband edge, passband and stopband ripple, and filter order. T, the sampling rate fp, the passband edge frequency fs, the stopband edge frequency , the maximum ripple Mathcad then calculates the remaining parameters and finds the zeros, poles, and coefficients for the filter transfer function. This procedure begins by computing the transfer function for a corresponding analog filter and then transforms the poles and roots of this function to produce the digital filter transfer function required. For more information on the bilinear transformation used in this application, see Section 13.1: Analog/Digital Lowpass Butterworth Filter. Background Elliptic filters, so called because they employ elliptic functions to generate the filter function, are useful because they have equiripple characteristics in the pass and stopband regions. This ensures that the lowest order filter can be used to meet design constraints. Elliptic filters, like all other lowpass filters, are feedback systems. All of the usual stability rules for feedback systems in the z-domain apply. Elliptic filters have all their zeros on the unit circle, and all their poles within the unit circle. For information on how to transform a continuous-time IIR filter to a discrete-time IIR filter, see Section 13.1: Analog/Digital Lowpass Butterworth Filter. For information on analog elliptical filter design, see Section 13.2: Analog Elliptic Filter Design. Mathcad Implementation This document implements a digital elliptic lowpass filter design. The definitions below of elliptic functions are used throughout the document to calculate filter characteristics. Elliptic Function Definitions TOL ≡10−4 Im (ϕ) Re (ϕ) ⌠ 1 ⌠ 1 U(ϕ,k)≡1i⋅ ⎮――――――dy+ ⎮―――――――――dy ‾‾‾‾‾‾‾‾‾‾‾‾2‾ ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾2‾ ⎮ 2 ⎮ 2 ⌡ 1−k ⋅sin(1j⋅y) ⌡ 1−k ⋅sin(1j⋅ Im(ϕ)+y) 0 0 ϕ≡11i+ sn(uk, )≡sin(root(U(ϕ,k)−u,ϕ)) π ― 2 ⌠ 1 L(k)≡⎮――――――dy ‾‾‾‾‾‾‾‾‾‾2‾ ⎮ 2 ⌡ 1−k ⋅sin(y) 0 ⎛⎛ ⎞⎞ 2 1− ‾1‾−‾k‾2‾ V(k)≡――――⋅L⎜⎜――――⎟⎟ 1+ ‾1‾−‾k‾2‾ ⎝⎜⎝⎜ 1+ ‾1‾−‾k‾2‾⎠⎟⎠⎟ K(k)≡if(k<.9999,L(k),V(k)) Design Specifications Sampling interval in seconds: T≔.001 1 implies a bandlimit (Hz) of: f ≔――=500 max 2⋅T Pass band edge in Hz: fp ≔100 Stop band edge in Hz: fs ≔105 Pass band ripple: δ1 ≔.05 Stop band ripple: δ2 ≔.05 Pass band edge is normalized to one: ωpp ≔1 2 ―⋅tan⎝⎛π⋅f ⋅T⎠⎞ For digital design, prewarp the stopband T s ωs ≔―――――=1.0537 edge to the corresponding analog value. s 2 ―⋅tan⎝⎛π⋅f ⋅T⎠⎞ T p Calculation of Filter Order Definitions of moduli: ‾‾2‾⋅‾δ‾−‾‾δ‾2‾‾‾ ε≔ ――1 ―1―― 2 1−2⋅δ1 +δ1 ε ‾‾‾‾2‾ k1 ≔――― k'1 ≔ 1−k1 ‾‾1‾‾‾‾ ――−1 2 δ2 ωp k≔―p― k'≔ ‾1‾−‾k‾2‾ ωss For correct calculations, check to see that k and k' are not too close to 1. For accuracy, they should be less than 1 - 10-9. −9 −9 check≔k<110− =1 check1 ≔k'1 <110− =1 ⎛ K(k)⋅K⎝⎛k'1⎠⎞ ⎞ N≔ceil⎜――――⎟ ⎝ K(k')⋅K⎝⎛k1⎠⎞ ⎠ The minimum filter order is: N=6 Finding the Zeros and Poles of the Transfer Function Zeros and poles of the transfer function are calculated using the elliptic functions. If the filter order is odd, there will be one real pole of order 1, in addition to several complex conjugate poles. KK≔K(k)=2.581 odd≔mod(N,2) I≔if(odd,21, ) ⎛ m ⎞ m≔0‥NI− c ≔I+2⋅ floor ― m ⎝⎜ 2 ⎠⎟ m ⎝⎛−1⎠⎞ ⋅1j sr ≔――――― m ⎛ KK ⎞ ksn⋅ c ⋅――,k ⎝⎜ m N ⎠⎟ l≔0‥N−1 conj(zl, )≔if⎝⎛mod(l,2)＝0,z,‾z⎠⎞ ⎛ l+mod(N,2) ⎞ KK ⎛ ⎛ 1 ⎞ ⎞ d ≔1mod− (N,2)+2⋅ floor ――――― v≔―――⋅U atan ―,k'1 =0.5015 l ⎜ ⎟ ⎜ ⎜ ⎟ ⎟ ⎝ 2 ⎠ NK⋅ ⎝⎛k1⎠⎞ ⎝ ⎝ ε ⎠ ⎠ ⎛ ⎛ d ⋅KK ⎞ ⎞ l sp ≔conj⎜1j⋅sn⎜――+1j⋅vk, ⎟,l⎟ l ⎝ ⎝ N ⎠ ⎠ Analog Transfer Function Use the poles and zeros of the system to construct the transfer function. It will be written as a factored expression of each pole and zero in the form (s - p1)(s - p2)(...), etc.. ∏sp l l A≔if⎝⎛mod(N,2)＝0,1−δ1 ,1⎠⎞⋅―― ∏sr m m The transfer function, H, normalized so that max H(j ) = 1: ∏⎛ssr− ⎞ m m ⎝ ⎠ Hs (s)≔A⋅―――― ∏⎛ssp− ⎞ l l ⎝ ⎠ Digital Transfer Function When you have calculated the roots and poles of the analog transfer function, the corresponding digital transfer function is given by 1 ⎛ z−1 ⎞ ( ) q≔―――― H(z)≔Hs ⎜q⋅――⎟ tan⎝⎛π⋅fp ⋅T⎠⎞ ⎝ z+1 ⎠ 1 f≔0‥―― 2⋅T 1.1 1 0.9 0.8 0.7 0.6 |H(exp(2j⋅π⋅fT⋅ ))| 0.5 0.4 0.3 0.2 0.1 0 02040 60 80 100 120 140 160 180 200 f Fig. 13.3.1 Frequency response of the digital transfer function Check magnitude at passband and stopband edges: |H⎝⎛exp⎝⎛2j⋅π⋅fp ⋅T⎠⎞⎠⎞|=0.95 |H⎝⎛exp⎝⎛2j⋅π⋅fs ⋅T⎠⎞⎠⎞|=0.0337 The zeros are qsr+ ⎛ qsr+ ⎞ m N − 1 a ≔――― a ≔if⎜odd,−1,―――⎟ m qsr− N − 1 ⎜ qsr− ⎟ m ⎝ N − 1 ⎠ The poles are qsp+ l b ≔―― l qsp− l 1.25 1 0.75 0.5 Im⎛b ⎞ 0.25 ⎝ l⎠ 0 Im⎛a ⎞ ⎝ l⎠ -0.25 Im⎝⎛e1j⋅ 4 ⋅ π ⋅ fT⋅ ⎠⎞ -0.5 -0.75 -1 -1.25 -1.25 -1 -0.75 -0.5 -0.25 0 0.25 0.5 0.75 1 1.25 Re⎛b ⎞ Re⎛a ⎞ Re⎝⎛e1j⋅ 4 ⋅ π ⋅ fT⋅ ⎠⎞ ⎝ l⎠ ⎝ l⎠ Fig. 13.3.2 Poles and zeros of the filter in the z-plane Polynomial Expansion To expand the transfer function into an Nth order polynomial, find the transfer function coefficients for numerator and denominator, and integrate according to Cauchy's theorem: HNUM(s)≔ ∏⎛sa− ⎞ l l ⎝ ⎠ HDEN(s)≔ ∏⎛sb− ⎞ l l ⎝ ⎠ Multiplying numerator coefficients by B will normalize H so that at frequency zero the response is 1 for N odd or 1 - for N even. HDEN(1) B≔――――⋅if⎝⎛odd,1,1−δ ⎠⎞ w≔0‥N HNUM(1) 1 1 ⌠ ⌡HNUM((exp(2j⋅π⋅x)))⋅cos(w⋅2⋅π⋅x) dx hnum ≔B⋅―0 ―――――――――――― w if(w＝01.5, , ) 1 ⌠ ⌡HDEN((exp(2j⋅π⋅x)))⋅cos(w⋅2⋅π⋅x) dx hden ≔―0 ―――――――――――― w if(w＝01.5, , ) Numerator Denominator coefficients: coefficients: ⎡ −12 ⎤ −16 0.043+9.775i⋅ 10 ⎡ + ⋅ ⎤ ⎡ ⎤ 0.48 8.882i 10 0 ⎢ −11 ⎥ ⎢ −16 ⎥ −0.144−4.98i⋅ 10 −2.849−8.882i⋅ 10 ⎢1⎥ ⎢ ⎥ ⎢ ⎥ −10 −16 ⎢2⎥ ⎢ 0.27+1.132i⋅ 10 ⎥ ⎢ 7.421−8.882i⋅ 10 ⎥ −10 w=⎢3⎥ hnum =⎢−0.321−1.464i⋅ 10 ⎥ hden =⎢−10.83 ⎥ w w ⎢ ⎥ ⎢ −10 ⎥ −16 4 0.27+1.132i⋅ 10 ⎢ 9.365−4.441i⋅ 10 ⎥ ⎢ ⎥ 5 ⎢ −11 ⎥ ⎢ −15 ⎥ −0.144−4.98i⋅ 10 −4.571−3.851i⋅ 10 ⎣⎢6⎦⎥ ⎢ ⎥ ⎢ ⎥ ⎣ 0.043+9.775i⋅ 10−12 ⎦ ⎣ 1+1.069i⋅ 10−15 ⎦.
Load more

Recommended publications
  • IIR Filterdesign
    UNIVERSITY OF OSLO IIR filterdesign Sverre Holm INF34700 Digital signalbehandling DEPARTMENT OF INFORMATICS UNIVERSITY OF OSLO Filterdesign 1. Spesifikasjon • Kjenne anven de lsen • Kjenne designmetoder (hva som er mulig, FIR/IIR) 2. Apppproksimas jon • Fokus her 3. Analyse • Filtre er som rege l spes ifiser t i fre kvens domene t • Også analysere i tid (fase, forsinkelse, ...) 4. Realisering • DSP, FPGA, PC: Matlab, C, Java ... DEPARTMENT OF INFORMATICS 2 UNIVERSITY OF OSLO Sources • The slides about Digital Filter Specifications have been a dap te d from s lides by S. Mitra, 2001 • Butterworth, Chebychev, etc filters are based on Wikipedia • Builds on Oppenheim & Schafer with Buck: Discrete-Time Signal Processing, 1999. DEPARTMENT OF INFORMATICS 3 UNIVERSITY OF OSLO IIR kontra FIR • IIR filtre er mer effektive enn FIR – færre koe ffisi en ter f or samme magnitu de- spesifikasjon • Men bare FIR kan gi eksakt lineær fase – Lineær fase symmetrisk h[n] ⇒ Nullpunkter symmetrisk om |z|=1 – Lineær fase IIR? ⇒ Poler utenfor enhetssirkelen ⇒ ustabilt • IIR kan også bli ustabile pga avrunding i aritme tikken, de t kan ikke FIR DEPARTMENT OF INFORMATICS 4 UNIVERSITY OF OSLO Ideal filters • Lavpass, høypass, båndpass, båndstopp j j HLP(e ) HHP(e ) 1 1 – 0 c c – c 0 c j j HBS(e ) HBP (e ) –1 1 – –c1 – – c2 c2 c1 c2 c2 c1 c1 DEPARTMENT OF INFORMATICS 5 UNIVERSITY OF OSLO Prototype low-pass filter • All filter design methods are specificed for low-pass only • It can be transformed into a high-pass filter • OiOr it can be p lace
    [Show full text]
  • 13.2 Analog Elliptic Filter Design
    CHAPTER 13 IIR FILTER DESIGN 13.2 Analog Elliptic Filter Design This document carries out design of an elliptic IIR lowpass analog filter. You define the following parameters: fp, the passband edge fs, the stopband edge frequency , the maximum ripple Mathcad then calculates the filter order and finds the zeros, poles, and coefficients for the filter transfer function. Background Elliptic filters, so called because they employ elliptic functions to generate the filter function, are useful because they have equiripple characteristics in the pass and stopband regions. This ensures that the lowest order filter can be used to meet design constraints. For information on how to transform a continuous-time IIR filter to a discrete-time IIR filter, see Section 13.1: Analog/Digital Lowpass Butterworth Filter. For information on the lowest order polynomial (as opposed to elliptic) filters, see Section 14: Chebyshev Polynomials. Mathcad Implementation This document implements an analog elliptic lowpass filter design. The definitions below of elliptic functions are used throughout the document to calculate filter characteristics. Elliptic Function Definitions TOL ≡10−5 Im (ϕ) Re (ϕ) ⌠ 1 ⌠ 1 U(ϕ,k)≡1i⋅ ⎮――――――dy+ ⎮―――――――――dy ‾‾‾‾‾‾‾‾‾‾‾‾2‾ ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾2‾ ⎮ 2 ⎮ 2 ⌡ 1−k ⋅sin(1j⋅y) ⌡ 1−k ⋅sin(1j⋅ Im(ϕ)+y) 0 0 ϕ≡1i sn(uk, )≡sin(root(U(ϕ,k)−u,ϕ)) π ― 2 ⌠ 1 L(k)≡⎮――――――dy ‾‾‾‾‾‾‾‾‾‾2‾ ⎮ 2 ⌡ 1−k ⋅sin(y) 0 ⎛⎛ ⎞⎞ 2 1− ‾1‾−‾k‾2‾ V(k)≡――――⋅L⎜⎜――――⎟⎟ 1+ ‾1‾−‾k‾2‾ ⎝⎜⎝⎜ 1+ ‾1‾−‾k‾2‾⎠⎟⎠⎟ K(k)≡if(k<.9999,L(k),V(k)) Design Specifications First, the passband edge is normalized to 1 and the maximum passband response is set at one.
    [Show full text]
  • Classic Filters There Are 4 Classic Analogue Filter Types: Butterworth, Chebyshev, Elliptic and Bessel. There Is No Ideal Filter
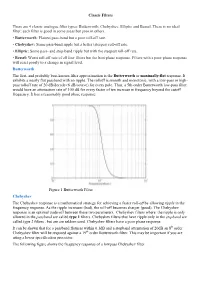
    Classic Filters There are 4 classic analogue filter types: Butterworth, Chebyshev, Elliptic and Bessel. There is no ideal filter; each filter is good in some areas but poor in others. • Butterworth: Flattest pass-band but a poor roll-off rate. • Chebyshev: Some pass-band ripple but a better (steeper) roll-off rate. • Elliptic: Some pass- and stop-band ripple but with the steepest roll-off rate. • Bessel: Worst roll-off rate of all four filters but the best phase response. Filters with a poor phase response will react poorly to a change in signal level. Butterworth The first, and probably best-known filter approximation is the Butterworth or maximally-flat response. It exhibits a nearly flat passband with no ripple. The rolloff is smooth and monotonic, with a low-pass or high- pass rolloff rate of 20 dB/decade (6 dB/octave) for every pole. Thus, a 5th-order Butterworth low-pass filter would have an attenuation rate of 100 dB for every factor of ten increase in frequency beyond the cutoff frequency. It has a reasonably good phase response. Figure 1 Butterworth Filter Chebyshev The Chebyshev response is a mathematical strategy for achieving a faster roll-off by allowing ripple in the frequency response. As the ripple increases (bad), the roll-off becomes sharper (good). The Chebyshev response is an optimal trade-off between these two parameters. Chebyshev filters where the ripple is only allowed in the passband are called type 1 filters. Chebyshev filters that have ripple only in the stopband are called type 2 filters , but are are seldom used.
    [Show full text]
  • Electronic Filters Design Tutorial - 3
    Electronic filters design tutorial - 3 High pass, low pass and notch passive filters In the first and second part of this tutorial we visited the band pass filters, with lumped and distributed elements. In this third part we will discuss about low-pass, high-pass and notch filters. The approach will be without mathematics, the goal will be to introduce readers to a physical knowledge of filters. People interested in a mathematical analysis will find in the appendix some books on the topic. Fig.2 ∗ The constant K low-pass filter: it was invented in 1922 by George Campbell and the Running the simulation we can see the response meaning of constant K is the expression: of the filter in fig.3 2 ZL* ZC = K = R ZL and ZC are the impedances of inductors and capacitors in the filter, while R is the terminating impedance. A look at fig.1 will be clarifying. Fig.3 It is clear that the sharpness of the response increase as the order of the filter increase. The ripple near the edge of the cutoff moves from Fig 1 monotonic in 3 rd order to ringing of about 1.7 dB for the 9 th order. This due to the mismatch of the The two filter configurations, at T and π are various sections that are connected to a 50 Ω displayed, all the reactance are 50 Ω and the impedance at the edges of the filter and filter cells are all equal. In practice the two series connected to reactive impedances between cells.
    [Show full text]
  • Performance Analysis of Analog Butterworth Low Pass Filter As Compared to Chebyshev Type-I Filter, Chebyshev Type-II Filter and Elliptical Filter
    Circuits and Systems, 2014, 5, 209-216 Published Online September 2014 in SciRes. http://www.scirp.org/journal/cs http://dx.doi.org/10.4236/cs.2014.59023 Performance Analysis of Analog Butterworth Low Pass Filter as Compared to Chebyshev Type-I Filter, Chebyshev Type-II Filter and Elliptical Filter Wazir Muhammad Laghari1, Mohammad Usman Baloch1, Muhammad Abid Mengal1, Syed Jalal Shah2 1Electrical Engineering Department, BUET, Khuzdar, Pakistan 2Computer Systems Engineering Department, BUET, Khuzdar, Pakistan Email: [email protected], [email protected], [email protected], [email protected] Received 29 June 2014; revised 31 July 2014; accepted 11 August 2014 Copyright © 2014 by authors and Scientific Research Publishing Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). http://creativecommons.org/licenses/by/4.0/ Abstract A signal is the entity that carries information. In the field of communication signal is the time varying quantity or functions of time and they are interrelated by a set of different equations, but some times processing of signal is corrupted due to adding some noise in the information signal and the information signal become noisy. It is very important to get the information from cor- rupted signal as we use filters. In this paper, Butterworth filter is designed for the signal analysis and also compared with other filters. It has maximally flat response in the pass band otherwise no ripples in the pass band. To meet the specification, 6th order Butterworth filter was chosen be- cause it is flat in the pass band and has no amount of ripples in the stop band.
    [Show full text]
  • Filters Matthew Spencer Harvey Mudd College E157 – Radio Frequency Circuit Design
    Department of Engineering Lecture 09: Filters Matthew Spencer Harvey Mudd College E157 – Radio Frequency Circuit Design 1 1 Department of Engineering Filter Specifications and the Filter Prototype Function Matthew Spencer Harvey Mudd College E157 – Radio Frequency Circuit Design 2 In this video we’re going to start talking about filters by defining a language that we use to describe them. 2 Department of Engineering Filters are Like Extended Matching Networks Vout Vout Vout + + + Vin Vin Vin - - - Absorbs power Absorbs power at one Absorbs power at one ω ω, but can pick Q in a range of ω 푉 푗휔 퐻 푗휔 = 푉 푗휔 ω ω ω 3 Filters are a natural follow on after talking about matching networks because you can think of them as an extension of the same idea. We showed that an L-match lets us absorb energy at one frequency (which is resonance) and reflect it at every other frequency, so we could think of an L match as a type of filter. That’s particularly obvious if we define a transfer function across an L match network from Vin to Vout, which would look like a narrow resonant peak. Adding more components in a pi match allowed us to control the shape of that peak and smear it out over more frequencies. So it stands to reason that by adding even more components to our matching network, we could control whether a signal is passed or reflected over a wider frequency. That turns out to be true, and the type of circuit that achieves this frequency response is referred to as an LC ladder filter.
    [Show full text]
  • And Elliptic Filter for Speech Signal Analysis Design And
    Design and Implementation of Butterworth, Chebyshev-I and Elliptic Filter for Speech Signal Analysis Prajoy Podder Md. Mehedi Hasan Md.Rafiqul Islam Department of ECE Department of ECE Department of EEE Khulna University of Khulna University of Khulna University of Engineering & Technology Engineering & Technology Engineering & Technology Khulna-9203, Bangladesh Khulna-9203, Bangladesh Khulna-9203, Bangladesh Mursalin Sayeed Department of EEE Khulna University of Engineering & Technology Khulna-9203, Bangladesh ABSTRACT and IIR filter. Analog electronic filters consisted of resistors, In the field of digital signal processing, the function of a filter capacitors and inductors are normally IIR filters [2]. On the is to remove unwanted parts of the signal such as random other hand, discrete-time filters (usually digital filters) based noise that is also undesirable. To remove noise from the on a tapped delay line that employs no feedback are speech signal transmission or to extract useful parts of the essentially FIR filters. The capacitors (or inductors) in the signal such as the components lying within a certain analog filter have a "memory" and their internal state never frequency range. Filters are broadly used in signal processing completely relaxes following an impulse. But after an impulse and communication systems in applications such as channel response has reached the end of the tapped delay line, the equalization, noise reduction, radar, audio processing, speech system has no further memory of that impulse. As a result, it signal processing, video processing, biomedical signal has returned to its initial state. Its impulse response beyond processing that is noisy ECG, EEG, EMG signal filtering, that point is exactly zero.
    [Show full text]
  • Design, Implementation, Comparison, and Performance Analysis Between Analog Butterworth and Chebyshev-I Low Pass Filter Using Approximation, Python and Proteus
    Design, Implementation, Comparison, and Performance analysis between Analog Butterworth and Chebyshev-I Low Pass Filter Using Approximation, Python and Proteus Navid Fazle Rabbi ( [email protected] ) Islamic University of Technology https://orcid.org/0000-0001-5085-2488 Research Article Keywords: Filter Design, Butterworth Filter, Chebyshev-I Filter Posted Date: February 16th, 2021 DOI: https://doi.org/10.21203/rs.3.rs-220218/v1 License: This work is licensed under a Creative Commons Attribution 4.0 International License. Read Full License Journal of Signal Processing Systems manuscript No. (will be inserted by the editor) Design, Implementation, Comparison, and Performance analysis between Analog Butterworth and Chebyshev-I Low Pass Filter Using Approximation, Python and Proteus Navid Fazle Rabbi Received: 24 January, 2021 / Accepted: date Abstract Filters are broadly used in signal processing and communication systems in noise reduction. Butterworth, Chebyshev-I Analog Low Pass Filters are developed and implemented in this paper. The filters are manually calculated using approximations and verified using Python Programming Language. Filters are also simulated in Proteus 8 Professional and implemented in the Hardware Lab using the necessary components. This paper also denotes the comparison and performance analysis of filters using Manual Computations, Hardware, and Software. Keywords Filter Design · Butterworth Filter · Chebyshev-I Filter 1 Introduction Filters play a crucial role in the field of digital and analog signal processing and communication networks. The standard analog filter architecture consists of two main components: the problem of approximation and the problem of synthesis. The primary purpose is to limit the signal to the specified frequency band or channel, or to model the input-output relationship of a specific device.[20][12] This paper revolves around the following two analog filters: – Butterworth Low Pass Filter – Chebyshev-I Low Pass Filter These filters play an essential role in alleviating unwanted signal parts.
    [Show full text]
  • Filter Approximation Concepts
    622 (ESS) 1 Filter Approximation Concepts How do you translate filter specifications into a mathematical expression which can be synthesized ? • Approximation Techniques Why an ideal Brick Wall Filter can not be implemented ? • Causality: Ideal filter is non-causal • Rationality: No rational transfer function of finite degree (n) can have such abrupt transition |H(jω)| h(t) Passband Stopband ω t -ωc ωc -Tc Tc 2 Filter Approximation Concepts Practical Implementations are given via window specs. |H(jω)| 1 Amax Amin ω ωc ωs Amax = Ap is the maximum attenuation in the passband Amin = As is the minimum attenuation in the stopband ωs-ωc is the Transition Width 3 Approximation Types of Lowpass Filter 1 Definitions Ap As Ripple = 1-Ap wc ws Stopband attenuation =As Filter specs Maximally flat (Butterworth) Passband (cutoff frequency) = wc Stopband frequency = ws Equal-ripple (Chebyshev) Elliptic 4 Approximation of the Ideal Lowpass Filter Since the ideal LPF is unrealizable, we will accept a small error in the passband, a non-zero transition band, and a finite stopband attenuation 1 퐻 푗휔 2 = 1 + 퐾 푗휔 2 |H(jω)| • 퐻 푗휔 : filter’s transfer function • 퐾 푗휔 : Characteristic function (deviation of 푇 푗휔 from unity) For 0 ≤ 휔 ≤ 휔푐 → 0 ≤ 퐾 푗휔 ≤ 1 For 휔 > 휔푐 → 퐾 푗휔 increases very fast Passband Stopband ω ωc 5 Maximally Flat Approximation (Butterworth) Stephen Butterworth showed in 1930 that the gain of an nth order maximally flat magnitude filter is given by 1 퐻 푗휔 2 = 퐻 푗휔 퐻 −푗휔 = 1 + 휀2휔2푛 퐾 푗휔 ≅ 0 in the passband in a maximally flat sense 푑푘 퐾 푗휔
    [Show full text]
  • Synthesis of Filters for Digital Wireless Communications
    Synthesis of Filters for Digital Wireless Communications Evaristo Musonda Submitted in accordance with the requirements for the degree of Doctor of Philosophy The University of Leeds Institute of Microwave and Photonics School of Electronic and Electrical Engineering December, 2015 i The candidate confirms that the work submitted is his own, except where work which has formed part of jointly-authored publications has been included. The contribution of the candidate and the other authors to this work has been explicitly indicated below. The candidate confirms that appropriate credit has been given within the report where reference has been made to the work of others. Chapter 2 to Chapter 6 are partly based on the following two papers: Musonda, E. and Hunter, I.C., Synthesis of general Chebyshev characteristic function for dual (single) bandpass filters. In Microwave Symposium (IMS), 2015 IEEE MTT-S International. 2015. Snyder, R.V., et al., Present and Future Trends in Filters and Multiplexers. Microwave Theory and Techniques, IEEE Transactions on, 2015. 63(10): p. 3324- 3360 E. Musonda developed the synthesis technique and wrote the first paper and section IV of the second invited paper. Professor Ian Hunter provided useful editorial comments, suggestions and corrections to the work. Chapter 3 is based on the following two papers: Musonda, E. and Hunter I.C., Design of generalised Chebyshev lowpass filters using coupled line/stub sections. In Microwave Symposium (IMS), 2015 IEEE MTT- S International. 2015. Musonda, E. and I.C. Hunter, Exact Design of a New Class of Generalised Chebyshev Low-Pass Filters Using Coupled Line/Stub Sections.
    [Show full text]
  • A Study of the Synthesis of 3-Port Electrical Filters with Chebyshev Or Elliptic Response Characteristics Bruce Vaughn Smith Iowa State University
    Iowa State University Capstones, Theses and Retrospective Theses and Dissertations Dissertations 1991 A study of the synthesis of 3-port electrical filters with Chebyshev or elliptic response characteristics Bruce Vaughn Smith Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/rtd Part of the Electrical and Electronics Commons Recommended Citation Smith, Bruce Vaughn, "A study of the synthesis of 3-port electrical filters with Chebyshev or elliptic response characteristics " (1991). Retrospective Theses and Dissertations. 9582. https://lib.dr.iastate.edu/rtd/9582 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Retrospective Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. INFORMATION TO USERS This manuscript has been reproduced from the microfilm master. UMI films the text directly from the original or copy submitted. Thus, some thesis and dissertation copies are in typewriter face, while others may be from any type of computer printer. The quality of this reproduction is dependent upon the quality of the copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs, print bleedthrough, substandard margins, and improper alignment can adversely affect reproduction. In the unlikely event that the author did not send UMI a complete manuscript and there are missing pages, these will be noted. Also, if unauthorized copyright material had to be removed, a note will indicate the deletion. Oversize materials (e.g., maps, drawings, charts) are reproduced by sectioning the original, beginning at the upper left-hand corner and continuing from left to right in equal sections with small overlaps.
    [Show full text]
  • Lecture Notes on Elliptic Filter Design
    Lecture Notes on Elliptic Filter Design Sophocles J. Orfanidis Department of Electrical & Computer Engineering Rutgers University, 94 Brett Road, Piscataway, NJ 08854-8058 Tel: 732-445-5017, e-mail: [email protected] November 20, 2006 Contents 1 Introduction 2 2 Jacobian Elliptic Functions 4 3 Elliptic Rational Function and the Degree Equation 11 4 Landen Transformations 14 5 Analog Elliptic Filter Design 16 6 Design Example 17 7 Butterworth and Chebyshev Designs 19 8 Highpass, Bandpass, and Bandstop Analog Filters 22 9 Digital Filter Design 26 10 Pole and Zero Transformations 26 11 Transformation of the Frequency Specifications 30 12 MATLAB Implementation and Examples 31 13 Frequency-Shifted Realizations 34 14 High-Order Parametric Equalizer Design 40 These notes and related MATLAB functions are available from the web page: www.ece.rutgers.edu/~orfanidi/ece521 1 1. Introduction Elliptic filters [1–11], also known as Cauer or Zolotarev filters, achieve the smallest filter order for the same specifications, or, the narrowest transition width for the same filter order, as compared to other filter types. On the negative side, they have the most nonlinear phase response over their passband. The following table compares the basic filter types with regard to filter order and phase response: In these notes, we are primarily concerned with elliptic filters. But we will also discuss briefly the design of Butterworth, Chebyshev-1, and Chebyshev-2 filters and present a unified method of designing all cases. We also discuss the design of digital IIR filters using the bilinear transformation method. The typical “brick wall” specifications for an analog lowpass filter are shown in Fig.
    [Show full text]