DOCSLIB.ORG

Synthesis of Filters for Digital Wireless Communications

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Synthesis of Filters for Digital Wireless Communications Synthesis of Filters for Digital Wireless Communications Evaristo Musonda Submitted in accordance with the requirements for the degree of Doctor of Philosophy The University of Leeds Institute of Microwave and Photonics School of Electronic and Electrical Engineering December, 2015 i The candidate confirms that the work submitted is his own, except where work which has formed part of jointly-authored publications has been included. The contribution of the candidate and the other authors to this work has been explicitly indicated below. The candidate confirms that appropriate credit has been given within the report where reference has been made to the work of others. Chapter 2 to Chapter 6 are partly based on the following two papers: Musonda, E. and Hunter, I.C., Synthesis of general Chebyshev characteristic function for dual (single) bandpass filters. In Microwave Symposium (IMS), 2015 IEEE MTT-S International. 2015. Snyder, R.V., et al., Present and Future Trends in Filters and Multiplexers. Microwave Theory and Techniques, IEEE Transactions on, 2015. 63(10): p. 3324- 3360 E. Musonda developed the synthesis technique and wrote the first paper and section IV of the second invited paper. Professor Ian Hunter provided useful editorial comments, suggestions and corrections to the work. Chapter 3 is based on the following two papers: Musonda, E. and Hunter I.C., Design of generalised Chebyshev lowpass filters using coupled line/stub sections. In Microwave Symposium (IMS), 2015 IEEE MTT- S International. 2015. Musonda, E. and I.C. Hunter, Exact Design of a New Class of Generalised Chebyshev Low-Pass Filters Using Coupled Line/Stub Sections. Microwave Theory and Techniques, IEEE Transactions on, 2015. PP(99): p. 1-11. Supervisor (Professor Ian Hunter) proposed the initial physical realisation of a basic section and reviewed the final papers. E. Musonda developed the initial idea, developed the complete synthesis technique including the required transfer functions and circuit transformations, and wrote the papers. Chapter 4 is based on the following paper: ii Musonda, E. and Hunter I.C., Microwave Bandpass Filters Using Re-Entrant Resonators. Microwave Theory and Techniques, IEEE Transactions on, 2015. 63(3): p. 954-964. Supervisor (Professor Ian Hunter) proposed the idea of integrated resonance and transmission zero using the re-entrant transmission line and reviewed the final paper. E. Musonda developed the equivalent circuits, synthesis and design theory and wrote the paper. This copy has been supplied on the understanding that it is copyright material and that no quotation from the report may be published without proper acknowledgement. © 2015 The University of Leeds and Evaristo Musonda iii Acknowledgements My utmost gratitude goes to Professor Ian Hunter, my supervisor and research chair of Royal Academy of Engineering/Radio Design Ltd - Microwave Signal Processing, for his exemplary role and encouragement during my PhD research work. I am grateful to Radio Design Limited for their technical support toward our research group at the University of Leeds. I am grateful to various individual supports from within School of Electronic and Electrical at Leeds University and my colleagues. I also incessantly thank my PhD sponsors namely the University of Leeds under the oversight of Professor Ian Hunter, the Beit Trust for part funding towards my PhD and RS Microwave for providing equipment funding. Lastly, I thank my family, my wife Caroline, my son Crescens, and daughters Whitney and Charlotte, for their endurance, emotional support and comfort rendered to me during the course of my research. I am forever indebted to my sister Mable, who has been like my mother and always been there for me whenever I needed someone to lean on. iv Abstract Firstly, a new synthesis method for the generation of the generalized Chebyshev characteristic polynomials has been presented. The general characteristic function is generated by a linear combination of Chebyshev basis characteristic functions. The basis functions for different filtering functions may easily be determined based on the number and position of reflection and transmission zeros. These basis functions enable direct synthesis of both lumped and distributed filter networks. Different filter functions including but not limited to low-pass, bandpass and dual bandpass filters, have been synthesised to demonstrate the general application of the synthesis method. Secondly, a new method for the design of a new class of distributed low-pass filter has been presented that enables exact realisation of the series short circuited transmission lines which are normally approximated via unit elements in other filter realisations. The filters are based on parallel coupled high impedance transmission lines which are terminated at one end in open-circuited stubs. The approach enables realisation of both finite and quarter-wave frequency transmission zeros hence giving improved stopband performance. A complete design is presented and the fabricated low-pass filter demonstrates excellent performance in good agreement with theory. Finally, design techniques for microwave bandpass filters using re-entrant resonators are presented. The key feature is that each re-entrant resonator in the filter generates a passband resonance and a finite frequency transmission zero, above the passband. Thus an Nth degree filter can have N finite frequency transmission zeros with a simple physical realization. A new synthesis technique for pseudo-elliptic low-pass filters suitable for designing re-entrant bandpass filter has also been show-cased. A physically symmetrical 5 pole re-entrant bandpass prototype filter with 5 transmission zeros above the passband was designed and fabricated. Measured results showed good correspondence with theories. v Table of Contents Acknowledgements .................................................................................... iv Abstract ........................................................................................................ v Table of Contents ........................................................................................ vi List of Tables ................................................................................................ x List of Figures ............................................................................................ xv Motivation .................................................................................................. xxi Thesis Organisation ................................................................................ xxv Chapter 1 Microwave Filters – Fundamentals ........................................... 1 1.1 Microwave Filter Networks – Analysis and Synthesis .................... 1 1.1.1 Filter Transfer Function, Characteristic Function and Characteristic Polynomials ..................................................... 2 1.1.2 S-Parameters, ABCD Matrix and Y Admittance Matrix .......... 8 1.1.3 Coupling Matrix Synthesis Method ...................................... 13 1.1.4 Cascaded Synthesis Method ............................................... 30 1.2 Design of Microwave Filters ......................................................... 38 1.2.1 Lumped Lowpass Prototype Filters ...................................... 38 1.2.2 Frequency Transformation and Impedance Scaling ............ 39 1.2.3 Distributed Elements Filters ................................................. 39 1.2.4 Numerical EM Techniques ................................................... 40 1.2.5 Other Design Considerations ............................................... 52 1.3 Conclusion ................................................................................... 53 Chapter 2 Method for Generating Generalised Chebyshev Polynomials ............................................................................................................. 54 2.1 Introduction .................................................................................. 54 2.2 Generalised Chebyshev Characteristic Function ......................... 54 2.3 General Recursive Technique - Determining the characteristic polynomials .................................................................................. 57 2.4 Basis Characteristic Functions ..................................................... 58 2.4.1 Lumped Generalised Chebyshev Low-pass Filters .............. 60 2.4.2 Distributed Generalised Chebyshev Low-pass Filters ......... 65 2.4.3 Lumped Generalised Chebyshev Bandpass Filters ............. 66 vi 2.4.4 Lumped Chebyshev Low-pass Prototype Filter for Interdigital Bandpass Filter .................................................................... 78 2.4.5 Distributed Generalised Chebyshev Bandpass Filters ......... 83 2.4.6 Lumped Chebyshev Narrow Dual Bandpass Filters ............ 86 2.4.7 Lumped Generalised Chebyshev Dual Bandpass Filters ..... 89 2.5 Procedure for Generating the Filter Characteristic Polynomials 101 2.6 Examples ................................................................................... 101 2.6.1 Direct Synthesis of Generalised Distributed Chebyshev Low- pass Filter .......................................................................... 102 2.6.2 Direct Synthesis of Generalised Distributed Bandpass Filter 104 2.7 Conclusion ................................................................................. 106 Chapter 3 Synthesis and Realisation of a New Class of Distributed Low- pass Filters ......................................................................................
Load more

Recommended publications
  • Theory and Techniques of Network Sensitivity Applied to Electrical Device Modelling and Circuit Design
    r THEORY AND TECHNIQUES OF NETWORK SENSITIVITY APPLIED TO ELECTRICAL DEVICE MODELLING AND CIRCUIT DESIGN • A thesis submitted for the degree of Doctor of Philosophy, in the Faculty of Engineering, University of London by Pedro Antonio Villalaz Communications Section, Department of Electrical Engineering Imperial College of Science and Technology, University of London September 1972 SUMMARY Chapter 1 is meant to provide a review of modelling as used in computer aided circuit design. Different types of model are distinguished according to their form or their application, and different levels of modelling are compared. Finally a scheme is described whereby models are considered as both isolated objects, and as objects embedded in their circuit environment. Chapter 2 deals with the optimization of linear equivalent circuit models. After some general considerations on the nature of the field of optimization, providing a limited survey, one particular optimization algorithm, the 'steepest descent method' is explained. A computer program has been written (in Fortran IV), using this method in an iterative process which allows to optimize the element values as well as (within certain limits) the topology of the models. Two different methods for the computation of the gradi- ent, which are employed in the program, are discussed in connection with their application. To terminate Chapter 2 some further details relevant to the optimization procedure are pointed out, and some computed examples illustrate the performance of the program. The next chapter can be regarded as a preparation for Chapters 4 and 5. An efficient method for the computation of large, change network sensitivity is described. A change in a network or equivalent circuit model element is simulated by means of an addi- tional current source introduced across that element.
    [Show full text]
  • Lecture 3: Transfer Function and Dynamic Response Analysis
    Transfer function approach Dynamic response Summary Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis Paweł Malczyk Division of Theory of Machines and Robots Institute of Aeronautics and Applied Mechanics Faculty of Power and Aeronautical Engineering Warsaw University of Technology October 17, 2019 © Paweł Malczyk. Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis 1 / 31 Transfer function approach Dynamic response Summary Outline 1 Transfer function approach 2 Dynamic response 3 Summary © Paweł Malczyk. Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis 2 / 31 Transfer function approach Dynamic response Summary Transfer function approach 1 Transfer function approach SISO system Definition Poles and zeros Transfer function for multivariable system Properties 2 Dynamic response 3 Summary © Paweł Malczyk. Basics of Automation and Control I Lecture 3: Transfer function and dynamic response analysis 3 / 31 Transfer function approach Dynamic response Summary SISO system Fig. 1: Block diagram of a single input single output (SISO) system Consider the continuous, linear time-invariant (LTI) system defined by linear constant coefficient ordinary differential equation (LCCODE): dny dn−1y + − + ··· + _ + = an n an 1 n−1 a1y a0y dt dt (1) dmu dm−1u = b + b − + ··· + b u_ + b u m dtm m 1 dtm−1 1 0 initial conditions y(0), y_(0),..., y(n−1)(0), and u(0),..., u(m−1)(0) given, u(t) – input signal, y(t) – output signal, ai – real constants for i = 1, ··· , n, and bj – real constants for j = 1, ··· , m. How do I find the LCCODE (1)? .
    [Show full text]
  • IIR Filterdesign
    UNIVERSITY OF OSLO IIR filterdesign Sverre Holm INF34700 Digital signalbehandling DEPARTMENT OF INFORMATICS UNIVERSITY OF OSLO Filterdesign 1. Spesifikasjon • Kjenne anven de lsen • Kjenne designmetoder (hva som er mulig, FIR/IIR) 2. Apppproksimas jon • Fokus her 3. Analyse • Filtre er som rege l spes ifiser t i fre kvens domene t • Også analysere i tid (fase, forsinkelse, ...) 4. Realisering • DSP, FPGA, PC: Matlab, C, Java ... DEPARTMENT OF INFORMATICS 2 UNIVERSITY OF OSLO Sources • The slides about Digital Filter Specifications have been a dap te d from s lides by S. Mitra, 2001 • Butterworth, Chebychev, etc filters are based on Wikipedia • Builds on Oppenheim & Schafer with Buck: Discrete-Time Signal Processing, 1999. DEPARTMENT OF INFORMATICS 3 UNIVERSITY OF OSLO IIR kontra FIR • IIR filtre er mer effektive enn FIR – færre koe ffisi en ter f or samme magnitu de- spesifikasjon • Men bare FIR kan gi eksakt lineær fase – Lineær fase symmetrisk h[n] ⇒ Nullpunkter symmetrisk om |z|=1 – Lineær fase IIR? ⇒ Poler utenfor enhetssirkelen ⇒ ustabilt • IIR kan også bli ustabile pga avrunding i aritme tikken, de t kan ikke FIR DEPARTMENT OF INFORMATICS 4 UNIVERSITY OF OSLO Ideal filters • Lavpass, høypass, båndpass, båndstopp j j HLP(e ) HHP(e ) 1 1 – 0 c c – c 0 c j j HBS(e ) HBP (e ) –1 1 – –c1 – – c2 c2 c1 c2 c2 c1 c1 DEPARTMENT OF INFORMATICS 5 UNIVERSITY OF OSLO Prototype low-pass filter • All filter design methods are specificed for low-pass only • It can be transformed into a high-pass filter • OiOr it can be p lace
    [Show full text]
  • Control Theory
    Control theory S. Simrock DESY, Hamburg, Germany Abstract In engineering and mathematics, control theory deals with the behaviour of dynamical systems. The desired output of a system is called the reference. When one or more output variables of a system need to follow a certain ref- erence over time, a controller manipulates the inputs to a system to obtain the desired effect on the output of the system. Rapid advances in digital system technology have radically altered the control design options. It has become routinely practicable to design very complicated digital controllers and to carry out the extensive calculations required for their design. These advances in im- plementation and design capability can be obtained at low cost because of the widespread availability of inexpensive and powerful digital processing plat- forms and high-speed analog IO devices. 1 Introduction The emphasis of this tutorial on control theory is on the design of digital controls to achieve good dy- namic response and small errors while using signals that are sampled in time and quantized in amplitude. Both transform (classical control) and state-space (modern control) methods are described and applied to illustrative examples. The transform methods emphasized are the root-locus method of Evans and fre- quency response. The state-space methods developed are the technique of pole assignment augmented by an estimator (observer) and optimal quadratic-loss control. The optimal control problems use the steady-state constant gain solution. Other topics covered are system identification and non-linear control. System identification is a general term to describe mathematical tools and algorithms that build dynamical models from measured data.
    [Show full text]
  • 13.2 Analog Elliptic Filter Design
    CHAPTER 13 IIR FILTER DESIGN 13.2 Analog Elliptic Filter Design This document carries out design of an elliptic IIR lowpass analog filter. You define the following parameters: fp, the passband edge fs, the stopband edge frequency , the maximum ripple Mathcad then calculates the filter order and finds the zeros, poles, and coefficients for the filter transfer function. Background Elliptic filters, so called because they employ elliptic functions to generate the filter function, are useful because they have equiripple characteristics in the pass and stopband regions. This ensures that the lowest order filter can be used to meet design constraints. For information on how to transform a continuous-time IIR filter to a discrete-time IIR filter, see Section 13.1: Analog/Digital Lowpass Butterworth Filter. For information on the lowest order polynomial (as opposed to elliptic) filters, see Section 14: Chebyshev Polynomials. Mathcad Implementation This document implements an analog elliptic lowpass filter design. The definitions below of elliptic functions are used throughout the document to calculate filter characteristics. Elliptic Function Definitions TOL ≡10−5 Im (ϕ) Re (ϕ) ⌠ 1 ⌠ 1 U(ϕ,k)≡1i⋅ ⎮――――――dy+ ⎮―――――――――dy ‾‾‾‾‾‾‾‾‾‾‾‾2‾ ‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾2‾ ⎮ 2 ⎮ 2 ⌡ 1−k ⋅sin(1j⋅y) ⌡ 1−k ⋅sin(1j⋅ Im(ϕ)+y) 0 0 ϕ≡1i sn(uk, )≡sin(root(U(ϕ,k)−u,ϕ)) π ― 2 ⌠ 1 L(k)≡⎮――――――dy ‾‾‾‾‾‾‾‾‾‾2‾ ⎮ 2 ⌡ 1−k ⋅sin(y) 0 ⎛⎛ ⎞⎞ 2 1− ‾1‾−‾k‾2‾ V(k)≡――――⋅L⎜⎜――――⎟⎟ 1+ ‾1‾−‾k‾2‾ ⎝⎜⎝⎜ 1+ ‾1‾−‾k‾2‾⎠⎟⎠⎟ K(k)≡if(k<.9999,L(k),V(k)) Design Specifications First, the passband edge is normalized to 1 and the maximum passband response is set at one.
    [Show full text]
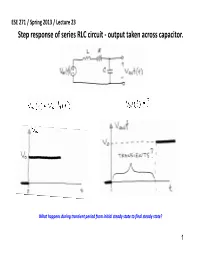
  • Step Response of Series RLC Circuit ‐ Output Taken Across Capacitor
    ESE 271 / Spring 2013 / Lecture 23 Step response of series RLC circuit ‐ output taken across capacitor. What happens during transient period from initial steady state to final steady state? 1 ESE 271 / Spring 2013 / Lecture 23 Transfer function of series RLC ‐ output taken across capacitor. Poles: Case 1: ‐‐two differen t real poles Case 2: ‐ two identical real poles ‐ complex conjugate poles Case 3: 2 ESE 271 / Spring 2013 / Lecture 23 Case 1: two different real poles. Step response of series RLC ‐ output taken across capacitor. Overdamped case –the circuit demonstrates relatively slow transient response. 3 ESE 271 / Spring 2013 / Lecture 23 Case 1: two different real poles. Freqqyuency response of series RLC ‐ output taken across capacitor. Uncorrected Bode Gain Plot Overdamped case –the circuit demonstrates relatively limited bandwidth 4 ESE 271 / Spring 2013 / Lecture 23 Case 2: two identical real poles. Step response of series RLC ‐ output taken across capacitor. Critically damped case –the circuit demonstrates the shortest possible rise time without overshoot. 5 ESE 271 / Spring 2013 / Lecture 23 Case 2: two identical real poles. Freqqyuency response of series RLC ‐ output taken across capacitor. Critically damped case –the circuit demonstrates the widest bandwidth without apparent resonance. Uncorrected Bode Gain Plot 6 ESE 271 / Spring 2013 / Lecture 23 Case 3: two complex poles. Step response of series RLC ‐ output taken across capacitor. Underdamped case – the circuit oscillates. 7 ESE 271 / Spring 2013 / Lecture 23 Case 3: two complex poles. Freqqyuency response of series RLC ‐ output taken across capacitor. Corrected Bode GiGain Plot Underdamped case –the circuit can demonstrate apparent resonant behavior.
    [Show full text]
  • Advanced Electronic Systems Damien Prêle
    Advanced Electronic Systems Damien Prêle To cite this version: Damien Prêle. Advanced Electronic Systems . Master. Advanced Electronic Systems, Hanoi, Vietnam. 2016, pp.140. cel-00843641v5 HAL Id: cel-00843641 https://cel.archives-ouvertes.fr/cel-00843641v5 Submitted on 18 Nov 2016 (v5), last revised 26 May 2021 (v8) HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. advanced electronic systems ST 11.7 - Master SPACE & AERONAUTICS University of Science and Technology of Hanoi Paris Diderot University Lectures, tutorials and labs 2016-2017 Damien PRÊLE [email protected] Contents I Filters 7 1 Filters 9 1.1 Introduction . .9 1.2 Filter parameters . .9 1.2.1 Voltage transfer function . .9 1.2.2 S plane (Laplace domain) . 11 1.2.3 Bode plot (Fourier domain) . 12 1.3 Cascading filter stages . 16 1.3.1 Polynomial equations . 17 1.3.2 Filter Tables . 20 1.3.3 The use of filter tables . 22 1.3.4 Conversion from low-pass filter . 23 1.4 Filter synthesis . 25 1.4.1 Sallen-Key topology . 25 1.5 Amplitude responses . 28 1.5.1 Filter specifications . 28 1.5.2 Amplitude response curves .
    [Show full text]
  • Frequency Response and Bode Plots
    1 Frequency Response and Bode Plots 1.1 Preliminaries The steady-state sinusoidal frequency-response of a circuit is described by the phasor transfer function Hj( ) . A Bode plot is a graph of the magnitude (in dB) or phase of the transfer function versus frequency. Of course we can easily program the transfer function into a computer to make such plots, and for very complicated transfer functions this may be our only recourse. But in many cases the key features of the plot can be quickly sketched by hand using some simple rules that identify the impact of the poles and zeroes in shaping the frequency response. The advantage of this approach is the insight it provides on how the circuit elements influence the frequency response. This is especially important in the design of frequency-selective circuits. We will first consider how to generate Bode plots for simple poles, and then discuss how to handle the general second-order response. Before doing this, however, it may be helpful to review some properties of transfer functions, the decibel scale, and properties of the log function. Poles, Zeroes, and Stability The s-domain transfer function is always a rational polynomial function of the form Ns() smm as12 a s m asa Hs() K K mm12 10 (1.1) nn12 n Ds() s bsnn12 b s bsb 10 As we have seen already, the polynomials in the numerator and denominator are factored to find the poles and zeroes; these are the values of s that make the numerator or denominator zero. If we write the zeroes as zz123,, zetc., and similarly write the poles as pp123,, p , then Hs( ) can be written in factored form as ()()()s zsz sz Hs() K 12 m (1.2) ()()()s psp12 sp n 1 © Bob York 2009 2 Frequency Response and Bode Plots The pole and zero locations can be real or complex.
    [Show full text]
  • Synthesis of Multiterminal RC Networks with the Aid of a Matrix
    SNTHES IS OF MULT ITER? INAL R C ETWO RKS WITH TIIF OF A I'.'ATRIX TRANSFOiATIO by 1-CHENG CHAG A THESIS submitted to OREGO STATF COLLEOEt in partial fulfillment of the requirements for the degree of !1ASTER OF SCIENCE Jurie 1961 APPROVED: Redacted for privacy Associate Professor of' Electrical Erigineerthg In Charge of Major Re6acted for privacy Head of the Department of Electrical Engineering Redacted for privacy Chairman of School Graduate Committee / Redacted for_privacy________ Dean of Graduate School Date thesis is presented August 9, 1960 Tyred by J nette Crane A CKNOWLEDGMENT This the3ls was accomplished under the supervision cf Associate professor, Hendrick Oorthuys. The author wishos to exnress his heartfelt thanks to Professor )orthuys for his ardent help and constant encourap;oment. TABL1 OF CONTENTS page Introductior , . i E. A &eneral ranfrnat1on Theory for Network Synthesis . 3 II. Synthesis of Multitermin.. al RC etworks from a rescribec Oren- Circuit Iì'ipedance atrix . 9 A. Open-Circuit Impedance latrix . 10 B. Node-Admittance 1atries . 11 C, Synthesis Procedure ....... 16 III. RC Ladder Synthesis . 23 Iv. Conclusion ....... 32 V. ii11io;raphy ...... * . 35 Apoendices ....... 37 LIST OF FIGURES Fig. Page 1. fetwork ytheszing Zm(s). Eq. (2.13) . 22 2 Alternato Realization of Z,"'). 22 Eq. (2.13) .......... ietwor1?. , A Ladder ........ 31 4. RC Ladder Realization of Z(s). r' L) .Lq. \*)...J.......... s s . s s S1TTHES I S OF ULT ITERM INAL R C NETWORKS WITH THE AID OF A MATRIX TRANSFOMATIO11 L'TRODUCT ION in the synthesis of passive networks, one of the most Imoortant problems is to determine realizability concU- tions.
    [Show full text]
  • Classic Filters There Are 4 Classic Analogue Filter Types: Butterworth, Chebyshev, Elliptic and Bessel. There Is No Ideal Filter
    Classic Filters There are 4 classic analogue filter types: Butterworth, Chebyshev, Elliptic and Bessel. There is no ideal filter; each filter is good in some areas but poor in others. • Butterworth: Flattest pass-band but a poor roll-off rate. • Chebyshev: Some pass-band ripple but a better (steeper) roll-off rate. • Elliptic: Some pass- and stop-band ripple but with the steepest roll-off rate. • Bessel: Worst roll-off rate of all four filters but the best phase response. Filters with a poor phase response will react poorly to a change in signal level. Butterworth The first, and probably best-known filter approximation is the Butterworth or maximally-flat response. It exhibits a nearly flat passband with no ripple. The rolloff is smooth and monotonic, with a low-pass or high- pass rolloff rate of 20 dB/decade (6 dB/octave) for every pole. Thus, a 5th-order Butterworth low-pass filter would have an attenuation rate of 100 dB for every factor of ten increase in frequency beyond the cutoff frequency. It has a reasonably good phase response. Figure 1 Butterworth Filter Chebyshev The Chebyshev response is a mathematical strategy for achieving a faster roll-off by allowing ripple in the frequency response. As the ripple increases (bad), the roll-off becomes sharper (good). The Chebyshev response is an optimal trade-off between these two parameters. Chebyshev filters where the ripple is only allowed in the passband are called type 1 filters. Chebyshev filters that have ripple only in the stopband are called type 2 filters , but are are seldom used.
    [Show full text]
  • Electronic Filters Design Tutorial - 3
    Electronic filters design tutorial - 3 High pass, low pass and notch passive filters In the first and second part of this tutorial we visited the band pass filters, with lumped and distributed elements. In this third part we will discuss about low-pass, high-pass and notch filters. The approach will be without mathematics, the goal will be to introduce readers to a physical knowledge of filters. People interested in a mathematical analysis will find in the appendix some books on the topic. Fig.2 ∗ The constant K low-pass filter: it was invented in 1922 by George Campbell and the Running the simulation we can see the response meaning of constant K is the expression: of the filter in fig.3 2 ZL* ZC = K = R ZL and ZC are the impedances of inductors and capacitors in the filter, while R is the terminating impedance. A look at fig.1 will be clarifying. Fig.3 It is clear that the sharpness of the response increase as the order of the filter increase. The ripple near the edge of the cutoff moves from Fig 1 monotonic in 3 rd order to ringing of about 1.7 dB for the 9 th order. This due to the mismatch of the The two filter configurations, at T and π are various sections that are connected to a 50 Ω displayed, all the reactance are 50 Ω and the impedance at the edges of the filter and filter cells are all equal. In practice the two series connected to reactive impedances between cells.
    [Show full text]
  • Performance Analysis of Analog Butterworth Low Pass Filter As Compared to Chebyshev Type-I Filter, Chebyshev Type-II Filter and Elliptical Filter
    Circuits and Systems, 2014, 5, 209-216 Published Online September 2014 in SciRes. http://www.scirp.org/journal/cs http://dx.doi.org/10.4236/cs.2014.59023 Performance Analysis of Analog Butterworth Low Pass Filter as Compared to Chebyshev Type-I Filter, Chebyshev Type-II Filter and Elliptical Filter Wazir Muhammad Laghari1, Mohammad Usman Baloch1, Muhammad Abid Mengal1, Syed Jalal Shah2 1Electrical Engineering Department, BUET, Khuzdar, Pakistan 2Computer Systems Engineering Department, BUET, Khuzdar, Pakistan Email: [email protected], [email protected], [email protected], [email protected] Received 29 June 2014; revised 31 July 2014; accepted 11 August 2014 Copyright © 2014 by authors and Scientific Research Publishing Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). http://creativecommons.org/licenses/by/4.0/ Abstract A signal is the entity that carries information. In the field of communication signal is the time varying quantity or functions of time and they are interrelated by a set of different equations, but some times processing of signal is corrupted due to adding some noise in the information signal and the information signal become noisy. It is very important to get the information from cor- rupted signal as we use filters. In this paper, Butterworth filter is designed for the signal analysis and also compared with other filters. It has maximally flat response in the pass band otherwise no ripples in the pass band. To meet the specification, 6th order Butterworth filter was chosen be- cause it is flat in the pass band and has no amount of ripples in the stop band.
    [Show full text]