Ordinary Muon Capture As a Probe of Virtual Transitions of $\Beta\Beta
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Discovery of the Isotopes with Z<= 10
Discovery of the Isotopes with Z ≤ 10 M. Thoennessen∗ National Superconducting Cyclotron Laboratory and Department of Physics and Astronomy, Michigan State University, East Lansing, MI 48824, USA Abstract A total of 126 isotopes with Z ≤ 10 have been identified to date. The discovery of these isotopes which includes the observation of unbound nuclei, is discussed. For each isotope a brief summary of the first refereed publication, including the production and identification method, is presented. arXiv:1009.2737v1 [nucl-ex] 14 Sep 2010 ∗Corresponding author. Email address: [email protected] (M. Thoennessen) Preprint submitted to Atomic Data and Nuclear Data Tables May 29, 2018 Contents 1. Introduction . 2 2. Discovery of Isotopes with Z ≤ 10........................................................................ 2 2.1. Z=0 ........................................................................................... 3 2.2. Hydrogen . 5 2.3. Helium .......................................................................................... 7 2.4. Lithium ......................................................................................... 9 2.5. Beryllium . 11 2.6. Boron ........................................................................................... 13 2.7. Carbon.......................................................................................... 15 2.8. Nitrogen . 18 2.9. Oxygen.......................................................................................... 21 2.10. Fluorine . 24 2.11. Neon........................................................................................... -

Photofission Cross Sections of 238U and 235U from 5.0 Mev to 8.0 Mev Robert Andrew Anderl Iowa State University
Iowa State University Capstones, Theses and Retrospective Theses and Dissertations Dissertations 1972 Photofission cross sections of 238U and 235U from 5.0 MeV to 8.0 MeV Robert Andrew Anderl Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/rtd Part of the Nuclear Commons, and the Oil, Gas, and Energy Commons Recommended Citation Anderl, Robert Andrew, "Photofission cross sections of 238U and 235U from 5.0 MeV to 8.0 MeV " (1972). Retrospective Theses and Dissertations. 4715. https://lib.dr.iastate.edu/rtd/4715 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Retrospective Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. INFORMATION TO USERS This dissertation was produced from a microfilm copy of the original document. While the most advanced technological means to photograph and reproduce this document have been used, the quality is heavily dependent upon the quality of the original submitted. The following explanation of techniques is provided to help you understand markings or patterns which may appear on this reproduction, 1. The sign or "target" for pages apparently lacking from the document photographed is "Missing Page(s)". If it was possible to obtain the missing page(s) or section, they are spliced into the film along with adjacent pages. This may have necessitated cutting thru an image and duplicating adjacent pages to insure you complete continuity, 2. -
R-Process: Observations, Theory, Experiment
r-process: observations, theory, experiment H. Schatz Michigan State University National Superconducting Cyclotron Laboratory Joint Institute for Nuclear Astrophysics 1. Observations: do we need s,r,p-process and LEPP? 2. r-process (and LEPP?) models 3. r-process experiments SNR 0103-72.6 Credit: NASA/CXC/PSU/S.Park et al. Origin of the heavy elements in the solar system s-process: secondary • nuclei can be studied Æ reliable calculations • site identified • understood? Not quite … r-process: primary • most nuclei out of reach • site unknown p-process: secondary (except for νp-process) Æ Look for metal poor`stars (Pagel, Fig 6.8) To learn about the r-process Heavy elements in Metal Poor Halo Stars CS22892-052 (Sneden et al. 2003, Cowan) 2 1 + solar r CS 22892-052 ) H / X CS22892-052 ( g o red (K) giant oldl stars - formed before e located in halo Galaxyc was mixed n distance: 4.7 kpc theya preserve local d mass ~0.8 M_sol n pollutionu from individual b [Fe/H]= −3.0 nucleosynthesisa events [Dy/Fe]= +1.7 recall: element number[X/Y]=log(X/Y)-log(X/Y)solar What does it mean: for heavy r-process? For light r-process? • stellar abundances show r-process • process is not universal • process is universal • or second process exists (not visible in this star) Conclusions depend on s-process Look at residuals: Star – solar r Solar – s-process – p-process s-processSimmerer from Simmerer (Cowan et etal.) al. /Lodders (Cowan et al.) s-processTravaglio/Lodders from Travaglio et al. -0.50 -0.50 -1.00 -1.00 -1.50 -1.50 log e log e -2.00 -2.00 -2.50 -2.50 30 40 50 60 70 80 90 30 40 50 60 70 80 90 Element number Element number ÆÆNeedNeed reliable reliable s-process s-process (models (models and and nu nuclearclear data, data, incl. -

Uses of Isotopic Neutron Sources in Elemental Analysis Applications
EG0600081 3rd Conference on Nuclear & Particle Physics (NUPPAC 01) 20 - 24 Oct., 2001 Cairo, Egypt USES OF ISOTOPIC NEUTRON SOURCES IN ELEMENTAL ANALYSIS APPLICATIONS A. M. Hassan Department of Reactor Physics Reactors Division, Nuclear Research Centre, Atomic Energy Authority. Cairo-Egypt. ABSTRACT The extensive development and applications on the uses of isotopic neutron in the field of elemental analysis of complex samples are largely occurred within the past 30 years. Such sources are used extensively to measure instantaneously, simultaneously and nondestruclively, the major, minor and trace elements in different materials. The low residual activity, bulk sample analysis and high accuracy for short lived elements are improved. Also, the portable isotopic neutron sources, offer a wide range of industrial and field applications. In this talk, a review on the theoretical basis and design considerations of different facilities using several isotopic neutron sources for elemental analysis of different materials is given. INTRODUCTION In principle there are two ways to use neutrons for elemental and isotopic abundance analysis in samples. One is the neutron activation analysis which we call it the "off-line" where the neutron - induced radioactivity is observed after the end of irradiation. The other one we call it the "on-line" where the capture gamma-rays is observed during the neutron bombardment. Actually, the sequence of events occurring during the most common type of nuclear reaction used in this analysis namely the neutron capture or (n, gamma) reaction, is well known for the people working in this field. The neutron interacts with the target nucleus via a non-elastic collision, a compound nucleus forms in an excited state. -

Correlated Neutron Emission in Fission
Correlated neutron emission in fission S. Lemaire , P. Talou , T. Kawano , D. G. Madland and M. B. Chadwick ¡ Nuclear Physics group, Los Alamos National Laboratory, Los Alamos, NM, 87545 Abstract. We have implemented a Monte-Carlo simulation of the fission fragments statistical decay by sequential neutron emission. Within this approach, we calculate both the center-of-mass and laboratory prompt neutron energy spectra, the ¢ prompt neutron multiplicity distribution P ν £ , and the average total number of emitted neutrons as a function of the mass of ¢ the fission fragment ν¯ A £ . Two assumptions for partitioning the total available excitation energy among the light and heavy fragments are considered. Preliminary results are reported for the neutron-induced fission of 235U (at 0.53 MeV neutron energy) and for the spontaneous fission of 252Cf. INTRODUCTION Methodology In this work, we extend the Los Alamos model [1] by A Monte Carlo approach allows to follow in detail any implementing a Monte-Carlo simulation of the statistical reaction chain and to record the result in a history-type decay (Weisskopf-Ewing) of the fission fragments (FF) file, which basically mimics the results of an experiment. by sequential neutron emission. This approach leads to a We first sample the FF mass and charge distributions, much more detailed picture of the decay process and var- and pick a pair of light and heavy nuclei that will then de- ious physical quantities can then be assessed: the center- cay by emitting zero, one or several neutrons. This decay of-mass and laboratory prompt neutron energy spectrum sequence is governed by neutrons emission probabilities ¤ ¤ ¥ N en ¥ , the prompt neutron multiplicity distribution P n , at different temperatures of the compound nucleus and the average number of emitted neutrons as a function of by the energies of the emitted neutrons. -

Nuclear Glossary
NUCLEAR GLOSSARY A ABSORBED DOSE The amount of energy deposited in a unit weight of biological tissue. The units of absorbed dose are rad and gray. ALPHA DECAY Type of radioactive decay in which an alpha ( α) particle (two protons and two neutrons) is emitted from the nucleus of an atom. ALPHA (ααα) PARTICLE. Alpha particles consist of two protons and two neutrons bound together into a particle identical to a helium nucleus. They are a highly ionizing form of particle radiation, and have low penetration. Alpha particles are emitted by radioactive nuclei such as uranium or radium in a process known as alpha decay. Owing to their charge and large mass, alpha particles are easily absorbed by materials and can travel only a few centimetres in air. They can be absorbed by tissue paper or the outer layers of human skin (about 40 µm, equivalent to a few cells deep) and so are not generally dangerous to life unless the source is ingested or inhaled. Because of this high mass and strong absorption, however, if alpha radiation does enter the body through inhalation or ingestion, it is the most destructive form of ionizing radiation, and with large enough dosage, can cause all of the symptoms of radiation poisoning. It is estimated that chromosome damage from α particles is 100 times greater than that caused by an equivalent amount of other radiation. ANNUAL LIMIT ON The intake in to the body by inhalation, ingestion or through the skin of a INTAKE (ALI) given radionuclide in a year that would result in a committed dose equal to the relevant dose limit . -

Neutron Emission Spectrometry for Fusion Reactor Diagnosis
Digital Comprehensive Summaries of Uppsala Dissertations from the Faculty of Science and Technology 1244 Neutron Emission Spectrometry for Fusion Reactor Diagnosis Method Development and Data Analysis JACOB ERIKSSON ACTA UNIVERSITATIS UPSALIENSIS ISSN 1651-6214 ISBN 978-91-554-9217-5 UPPSALA urn:nbn:se:uu:diva-247994 2015 Dissertation presented at Uppsala University to be publicly examined in Polhemsalen, Ångströmlaboratoriet, Lägerhyddsvägen 1, Uppsala, Friday, 22 May 2015 at 09:15 for the degree of Doctor of Philosophy. The examination will be conducted in English. Faculty examiner: Dr Andreas Dinklage (Max-Planck-Institut für Plasmaphysik, Greifswald, Germany). Abstract Eriksson, J. 2015. Neutron Emission Spectrometry for Fusion Reactor Diagnosis. Method Development and Data Analysis. Digital Comprehensive Summaries of Uppsala Dissertations from the Faculty of Science and Technology 1244. 92 pp. Uppsala: Acta Universitatis Upsaliensis. ISBN 978-91-554-9217-5. It is possible to obtain information about various properties of the fuel ions deuterium (D) and tritium (T) in a fusion plasma by measuring the neutron emission from the plasma. Neutrons are produced in fusion reactions between the fuel ions, which means that the intensity and energy spectrum of the emitted neutrons are related to the densities and velocity distributions of these ions. This thesis describes different methods for analyzing data from fusion neutron measurements. The main focus is on neutron spectrometry measurements, using data used collected at the tokamak fusion reactor JET in England. Several neutron spectrometers are installed at JET, including the time-of-flight spectrometer TOFOR and the magnetic proton recoil (MPRu) spectrometer. Part of the work is concerned with the calculation of neutron spectra from given fuel ion distributions. -

16. Fission and Fusion Particle and Nuclear Physics
16. Fission and Fusion Particle and Nuclear Physics Dr. Tina Potter Dr. Tina Potter 16. Fission and Fusion 1 In this section... Fission Reactors Fusion Nucleosynthesis Solar neutrinos Dr. Tina Potter 16. Fission and Fusion 2 Fission and Fusion Most stable form of matter at A~60 Fission occurs because the total Fusion occurs because the two Fission low A nuclei have too large a Coulomb repulsion energy of p's in a surface area for their volume. nucleus is reduced if the nucleus The surface area decreases Fusion splits into two smaller nuclei. when they amalgamate. The nuclear surface The Coulomb energy increases, energy increases but its influence in the process, is smaller. but its effect is smaller. Expect a large amount of energy released in the fission of a heavy nucleus into two medium-sized nuclei or in the fusion of two light nuclei into a single medium nucleus. a Z 2 (N − Z)2 SEMF B(A; Z) = a A − a A2=3 − c − a + δ(A) V S A1=3 A A Dr. Tina Potter 16. Fission and Fusion 3 Spontaneous Fission Expect spontaneous fission to occur if energy released E0 = B(A1; Z1) + B(A2; Z2) − B(A; Z) > 0 Assume nucleus divides as A , Z A1 Z1 A2 Z2 1 1 where = = y and = = 1 − y A, Z A Z A Z A2, Z2 2 2=3 2=3 2=3 Z 5=3 5=3 from SEMF E0 = aSA (1 − y − (1 − y) ) + aC (1 − y − (1 − y) ) A1=3 @E0 maximum energy released when @y = 0 @E 2 2 Z 2 5 5 0 = a A2=3(− y −1=3 + (1 − y)−1=3) + a (− y 2=3 + (1 − y)2=3) = 0 @y S 3 3 C A1=3 3 3 solution y = 1=2 ) Symmetric fission Z 2 2=3 max. -

Nuclear Mass and Stability
CHAPTER 3 Nuclear Mass and Stability Contents 3.1. Patterns of nuclear stability 41 3.2. Neutron to proton ratio 43 3.3. Mass defect 45 3.4. Binding energy 47 3.5. Nuclear radius 48 3.6. Semiempirical mass equation 50 3.7. Valley of $-stability 51 3.8. The missing elements: 43Tc and 61Pm 53 3.8.1. Promethium 53 3.8.2. Technetium 54 3.9. Other modes of instability 56 3.10. Exercises 56 3.11. Literature 57 3.1. Patterns of nuclear stability There are approximately 275 different nuclei which have shown no evidence of radioactive decay and, hence, are said to be stable with respect to radioactive decay. When these nuclei are compared for their constituent nucleons, we find that approximately 60% of them have both an even number of protons and an even number of neutrons (even-even nuclei). The remaining 40% are about equally divided between those that have an even number of protons and an odd number of neutrons (even-odd nuclei) and those with an odd number of protons and an even number of neutrons (odd-even nuclei). There are only 5 stable nuclei known which have both 2 6 10 14 an odd number of protons and odd number of neutrons (odd-odd nuclei); 1H, 3Li, 5B, 7N, and 50 23V. It is significant that the first stable odd-odd nuclei are abundant in the very light elements 2 (the low abundance of 1H has a special explanation, see Ch. 17). The last nuclide is found in low isotopic abundance (0.25%) and we cannot be certain that this nuclide is not unstable to radioactive decay with extremely long half-life. -
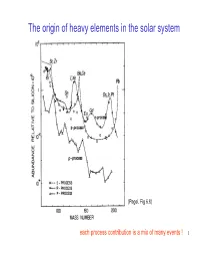
The Origin of Heavy Elements in the Solar System
The origin of heavy elements in the solar system (Pagel, Fig 6.8) each process contribution is a mix of many events ! 1 Abundance pattern: “Finger print ” of the r-process ? Tellurium and Xenon Peak Platinum Peak Solar abundance of the elements r-process only (subtract s,p processes) ) 6 Abundance (Si(Si = =Abundance Abundance 10 10 Element number (Z) But: sun formed ~10 billion years after big bang: many stars contributed to elements This could be an accidental combination of many different “fingerprints ” ? Find a star that is much older than the sun to find “fingerprint ” of single event 2 Heavy elements in Metal Poor Halo Stars CS22892-052 red (K) giant located in halo distance: 4.7 kpc mass ~0.8 M_sol [Fe/H]= −−−3.0 recall: [Dy/Fe]= +1.7 [X/Y]=log(X/Y)-log(X/Y) solar old stars - formed before Galaxy was mixed they preserve local pollution from individual nucleosynthesis events 3 A single (or a few) r -process event(s) CS22892-052 (Sneden et al. 2003) 1 solar r Cosmo Chronometer 0 -1 NEW: CS31082-001 with U (Cayrel et al. 2001) -2 40 50 60 70 80 90 Age: 16+ - 3 Gyr element number (Schatz et al. 2002 other, second ApJ 579, 626) r-process to fill main r-process this up ? matches exactly solar r-pattern (weak r-process) conclusions ? 4 More rII stars Solar r-process elements from many events J. Cowan 5 A surprise J. Cowan A new process contributing to Y, Sr, Zr (early Galaxy only? Solar? In this case: some traditional “r-contributions” to solar are not (main) r-process) Call it LEPP (Light Element Primary Process) 6 Overview heavy -

BETA DECAY in Β-Decay Processes, the Mass Number a Is Constant, but the Proton and Neutron Numbers Change As the Parent Decays
BETA DECAY In β-decay processes, the mass number A is constant, but the proton and neutron numbers change as the parent decays to a daughter that is better bound with lower mass. In β− decay, a neutron transforms into a proton, and an electron is emitted to conserve charge. Overall, Z Z +1.Inβ+ decay, a proton transforms into a neutron, an electron is emitted! and Z Z 1. In a third process, called electron capture or EC decay, the nucleus! − swallows an atomic electron, most likely from the atomic 1s state, and a proton converts to a neutron. The overall the e↵ect on the radioactive nucleus is the same in β+ decay. The electrons (or positrons) emitted in the first two types of β decay have continuous kinetic energies, up to an endpoint which depends on the particular species decaying, but is usually of the order of 1 MeV. The electrons (or positrons) cannot pre-exist inside the nucleus. A simple uncertainty estimate suggests that if they did, the endpoint would be much higher in energy: If it did pre-exist, then the electron would be somewhere in the nucleus beforehand, with an uncertainty in position equal to the size of the nucleus, 1/3 ∆x r0A 5 fm, in a medium mass nucleus. ⇠ ⇠ ¯h 197 MeV.fm/c The uncertainty in momentum is then ∆p = ∆x = 5 fm =40MeV/c. So the smallest momentum that the endpoint could be would correspond to 40 MeV/c. The corresponding smallest endpoint energy would be: E2 = c2p2 + m2c4 c2p2 =40MeV. -

Physics and Technology of Spallation Neutron Sources
CH9900035 to o CO a PAUL SCHERRER INSTITUT PSI Bericht Nr. 98-06 m August 1998 53 ISSN 1019-0643 0. Solid State Research at Large Facilities Physics and Technology of Spallation Neutron Sources G. S. Bauer Paul Scherrer Institut CH - 5232 Villigen PSI Telefon 056 310 21 11 30-49 Telefax 056 310 21 99 PSI-Bericht Nr. 98-06 Physics and Technology of Spallation Neutron Sources G.S. Bauer Spallation Neutron Source Division Paul Scherrer Institut CH-5232 Villigen PSI, Switzerland [email protected] Lecture notes of a course given at the 1998 Frederic Jolliot Summer School in Cadarache, France, August 16-27, 1998 intended for publication, in revised form, in a Special Issue of Nuclear Instruments and Methods A. Paul Scherrer Institut Solid State Research at Large Facilities August 1998 Physics and Technology of Spallation Neutron Sources1 G.S. Bauer Spallation Neutron Source Division Paul Scherrer Institut CH-5232 Villigen PSI, Switzerland [email protected] Abstract Next to fission and fusion, spallation is an efficient process for releasing neutrons from nuclei. Unlike the other two reactions, it is an endothermal process and can, therefore, not be used per se in energy generation. In order to sustain a spallation reaction, an energetic beam of particles, most commonly protons, must be supplied onto a heavy target. Spallation can, however, play an important role as a source of neutrons whose flux can be easily controlled via the driving beam. Up to a few GeV of energy, the neutron production is roughly proportional to the beam power. Although sophisticated Monte Carlo codes exist to compute all aspects of a spallation facility, many features can be understood on the basis of simple physics arguments.