Module 4/Melody,Harmony,Texture
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
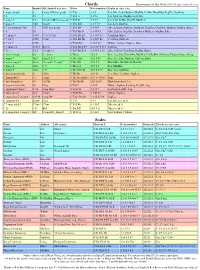
Chords and Scales 30/09/18 3:21 PM
Chords and Scales 30/09/18 3:21 PM Chords Charts written by Mal Webb 2014-18 http://malwebb.com Name Symbol Alt. Symbol (best first) Notes Note numbers Scales (in order of fit). C major (triad) C Cmaj, CM (not good) C E G 1 3 5 Ion, Mix, Lyd, MajPent, MajBlu, DoHar, HarmMaj, RagPD, DomPent C 6 C6 C E G A 1 3 5 6 Ion, MajPent, MajBlu, Lyd, Mix C major 7 C∆ Cmaj7, CM7 (not good) C E G B 1 3 5 7 Ion, Lyd, DoHar, RagPD, MajPent C major 9 C∆9 Cmaj9 C E G B D 1 3 5 7 9 Ion, Lyd, MajPent C 7 (or dominant 7th) C7 CM7 (not good) C E G Bb 1 3 5 b7 Mix, LyDom, PhrDom, DomPent, RagCha, ComDim, MajPent, MajBlu, Blues C 9 C9 C E G Bb D 1 3 5 b7 9 Mix, LyDom, RagCha, DomPent, MajPent, MajBlu, Blues C 7 sharp 9 C7#9 C7+9, C7alt. C E G Bb D# 1 3 5 b7 #9 ComDim, Blues C 7 flat 9 C7b9 C7alt. C E G Bb Db 1 3 5 b7 b9 ComDim, PhrDom C 7 flat 5 C7b5 C E Gb Bb 1 3 b5 b7 Whole, LyDom, SupLoc, Blues C 7 sharp 11 C7#11 Bb+/C C E G Bb D F# 1 3 5 b7 9 #11 LyDom C 13 C 13 C9 add 13 C E G Bb D A 1 3 5 b7 9 13 Mix, LyDom, DomPent, MajBlu, Blues C minor (triad) Cm C-, Cmin C Eb G 1 b3 5 Dor, Aeo, Phr, HarmMin, MelMin, DoHarMin, MinPent, Ukdom, Blues, Pelog C minor 7 Cm7 Cmin7, C-7 C Eb G Bb 1 b3 5 b7 Dor, Aeo, Phr, MinPent, UkDom, Blues C minor major 7 Cm∆ Cm maj7, C- maj7 C Eb G B 1 b3 5 7 HarmMin, MelMin, DoHarMin C minor 6 Cm6 C-6 C Eb G A 1 b3 5 6 Dor, MelMin C minor 9 Cm9 C-9 C Eb G Bb D 1 b3 5 b7 9 Dor, Aeo, MinPent C diminished (triad) Cº Cdim C Eb Gb 1 b3 b5 Loc, Dim, ComDim, SupLoc C diminished 7 Cº7 Cdim7 C Eb Gb A(Bbb) 1 b3 b5 6(bb7) Dim C half diminished Cø -

Year 9 Blues & Improvisation Duration 13-14 Weeks
Topic: Year 9 Blues & Improvisation Duration 13-14 Weeks Key vocabulary: Core knowledge questions Powerful knowledge crucial to commit to long term Links to previous and future topics memory 12-Bar Blues, Blues 45. What are the key features of blues music? • Learn about the history, origins and Links to chromatic Notes from year 8. Chord Sequence, 46. What are the main chords used in the 12-bar blues sequence? development of the Blues and its characteristic Links to Celtic Music from year 8 due to Improvisation 47. What other styles of music led to the development of blues 12-bar Blues structure exploring how a walking using improvisation. Links to form & Syncopation Blues music? bass line is developed from a chord structure from year 9 and Hooks & Riffs Scale Riffs 48. Can you explain the term improvisation and what does it mean progression. in year 9. Fills in blues music? • Explore the effect of adding a melodic Solos 49. Can you identify where the chords change in a 12-bar blues improvisation using the Blues scale and the Make links to music from other cultures Chords I, IV, V, sequence? effect which “swung”rhythms have as used in and traditions that use riff and ostinato- Blues Song Lyrics 50. Can you explain what is meant by ‘Singin the Blues’? jazz and blues music. based structures, such as African Blues Songs 51. Why did music play an important part in the lives of the African • Explore Ragtime Music as a type of jazz style spirituals and other styles of Jazz. -

Minor Pentatonic & Blues- the Five Box Shapes
Minor Pentatonic & Blues- The Five Box Shapes Now we will add one note to the minor pentatonic scale and turn it into the six-note blues scale. Pentatonic & Blues scales are the most commonly used scales in most genres of music. We can add the flat 5, (b5), or blue note to the pentatonic scale, making it a six-note scale called the Blues Scale. That b5, or blue note, adds a lot of tension and color to the scale. These are “must-know” scales especially for blues and rock so be sure to memorize them and add them to your soloing repertoire. Most of the time when soloing with minor pentatonic scales you can also use the blues scale. To be safe, at first, use the blue note more in passing for color, don’t hang on it too long. Hanging on that flat five too long can sound a bit dissonant. It’s a great note though, so experiment with it and let your ear guide you. The five box shapes illustrated below cover the entire neck. These five positions are the architecture to build licks and runs as well as to connect into longer expanded scales. To work freely across the entire neck you will want to memorize all five positions as well as the two expanded scales illustrated on the next page. These scale shapes are moveable. The key is determined by the root notes illustrated in black. If you want to solo in G minor pentatonic play box #1 using your first finger starting at the 3rd fret on the low E-string and play the shape from there. -

3 Manual Microtonal Organ Ruben Sverre Gjertsen 2013
3 Manual Microtonal Organ http://www.bek.no/~ruben/Research/Downloads/software.html Ruben Sverre Gjertsen 2013 An interface to existing software A motivation for creating this instrument has been an interest for gaining experience with a large range of intonation systems. This software instrument is built with Max 61, as an interface to the Fluidsynth object2. Fluidsynth offers possibilities for retuning soundfont banks (Sf2 format) to 12-tone or full-register tunings. Max 6 introduced the dictionary format, which has been useful for creating a tuning database in text format, as well as storing presets. This tuning database can naturally be expanded by users, if tunings are written in the syntax read by this instrument. The freely available Jeux organ soundfont3 has been used as a default soundfont, while any instrument in the sf2 format can be loaded. The organ interface The organ window 3 MIDI Keyboards This instrument contains 3 separate fluidsynth modules, named Manual 1-3. 3 keysliders can be played staccato by the mouse for testing, while the most musically sufficient option is performing from connected MIDI keyboards. Available inputs will be automatically recognized and can be selected from the menus. To keep some of the manuals silent, select the bottom alternative "to 2ManualMicroORGANircamSpat 1", which will not receive MIDI signal, unless another program (for instance Sibelius) is sending them. A separate menu can be used to select a foot trigger. The red toggle must be pressed for this to be active. This has been tested with Behringer FCB1010 triggers. Other devices could possibly require adjustments to the patch. -

Enharmonic Substitution in Bernard Herrmann's Early Works
Enharmonic Substitution in Bernard Herrmann’s Early Works By William Wrobel In the course of my research of Bernard Herrmann scores over the years, I’ve recently come across what I assume to be an interesting notational inconsistency in Herrmann’s scores. Several months ago I began to earnestly focus on his scores prior to 1947, especially while doing research of his Citizen Kane score (1941) for my Film Score Rundowns website (http://www.filmmusic.cjb.net). Also I visited UCSB to study his Symphony (1941) and earlier scores. What I noticed is that roughly prior to 1947 Herrmann tended to consistently write enharmonic notes for certain diatonic chords, especially E substituted for Fb (F-flat) in, say, Fb major 7th (Fb/Ab/Cb/Eb) chords, and (less frequently) B substituted for Cb in, say, Ab minor (Ab/Cb/Eb) triads. Occasionally I would see instances of other note exchanges such as Gb for F# in a D maj 7 chord. This enharmonic substitution (or “equivalence” if you prefer that term) is overwhelmingly consistent in Herrmann’ notational practice in scores roughly prior to 1947, and curiously abandoned by the composer afterwards. The notational “inconsistency,” therefore, relates to the change of practice split between these two periods of Herrmann’s career, almost a form of “Before” and “After” portrayal of his notational habits. Indeed, after examination of several dozens of his scores in the “After” period, I have seen (so far in this ongoing research) only one instance of enharmonic substitution similar to what Herrmann engaged in before 1947 (see my discussion in point # 19 on Battle of Neretva). -

Finale Transposition Chart, by Makemusic User Forum Member Motet (6/5/2016) Trans
Finale Transposition Chart, by MakeMusic user forum member Motet (6/5/2016) Trans. Sounding Written Inter- Key Usage (Some Common Western Instruments) val Alter C Up 2 octaves Down 2 octaves -14 0 Glockenspiel D¯ Up min. 9th Down min. 9th -8 5 D¯ Piccolo C* Up octave Down octave -7 0 Piccolo, Celesta, Xylophone, Handbells B¯ Up min. 7th Down min. 7th -6 2 B¯ Piccolo Trumpet, Soprillo Sax A Up maj. 6th Down maj. 6th -5 -3 A Piccolo Trumpet A¯ Up min. 6th Down min. 6th -5 4 A¯ Clarinet F Up perf. 4th Down perf. 4th -3 1 F Trumpet E Up maj. 3rd Down maj. 3rd -2 -4 E Trumpet E¯* Up min. 3rd Down min. 3rd -2 3 E¯ Clarinet, E¯ Flute, E¯ Trumpet, Soprano Cornet, Sopranino Sax D Up maj. 2nd Down maj. 2nd -1 -2 D Clarinet, D Trumpet D¯ Up min. 2nd Down min. 2nd -1 5 D¯ Flute C Unison Unison 0 0 Concert pitch, Horn in C alto B Down min. 2nd Up min. 2nd 1 -5 Horn in B (natural) alto, B Trumpet B¯* Down maj. 2nd Up maj. 2nd 1 2 B¯ Clarinet, B¯ Trumpet, Soprano Sax, Horn in B¯ alto, Flugelhorn A* Down min. 3rd Up min. 3rd 2 -3 A Clarinet, Horn in A, Oboe d’Amore A¯ Down maj. 3rd Up maj. 3rd 2 4 Horn in A¯ G* Down perf. 4th Up perf. 4th 3 -1 Horn in G, Alto Flute G¯ Down aug. 4th Up aug. 4th 3 6 Horn in G¯ F# Down dim. -

Written Vs. Sounding Pitch
Written Vs. Sounding Pitch Donald Byrd School of Music, Indiana University January 2004; revised January 2005 Thanks to Alan Belkin, Myron Bloom, Tim Crawford, Michael Good, Caitlin Hunter, Eric Isaacson, Dave Meredith, Susan Moses, Paul Nadler, and Janet Scott for information and for comments on this document. "*" indicates scores I haven't seen personally. It is generally believed that converting written pitch to sounding pitch in conventional music notation is always a straightforward process. This is not true. In fact, it's sometimes barely possible to convert written pitch to sounding pitch with real confidence, at least for anyone but an expert who has examined the music closely. There are many reasons for this; a list follows. Note that the first seven or eight items are specific to various instruments, while the others are more generic. Note also that most of these items affect only the octave, so errors are easily overlooked and, as a practical matter, not that serious, though octave errors can result in mistakes in identifying the outer voices. The exceptions are timpani notation and accidental carrying, which can produce semitone errors; natural harmonics notated at fingered pitch, which can produce errors of a few large intervals; baritone horn and euphonium clef dependencies, which can produce errors of a major 9th; and scordatura and C scores, which can lead to errors of almost any amount. Obviously these are quite serious, even disasterous. It is also generally considered that the difference between written and sounding pitch is simply a matter of transposition. Several of these cases make it obvious that that view is correct only if the "transposition" can vary from note to note, and if it can be one or more octaves, or a smaller interval plus one or more octaves. -

Scale Theory -Blues Scale
Scale Theory -Blues Scale Remember we derived the C scale using 221-2221 for the number of half steps? C Db D Eb E F G Ab A Bb B C C 2 D 2 E 1 F2 G 2 A 2 B 1 C - C major scale is C D E F G A B C The major pentatonic (5 tone) scale is CDEGA or the 1, 2, 3, 5 and 6 of the scale The minor pentatonic (5 tone) scale is CEbFGBb or the 1, b3, 4, 5 and b7 The blues scale can be found like that too -adds a b5 to the minor pentatonic scale We could also use a formula: 3 2 1 1 3 2 (steps) - Let's start with the key of C First, write all possible notes C Db D Eb E F Gb G Ab A Bb B C use the formula: C 3 Eb 2 F 1 Gb 1 G 3 Bb 2 C Position in major scale: 1 b3 4 b5 5 b7 1 Therefore, the C blues scale is C Eb F Gb G Bb C *This method will work for the blues scale in any key - try it for the A Blues scale Find the A blues scale: write all possible notes A A# B C C# D D# E F F# G G#A use the formula for the blues scale 321-132 A 3 C 2 D1D#1E 3 G 2 A Position in major scale: 1 b3 4 b5 5 b7 1 Therefore, the A major scale is A C D D# E G A You can play the blues scale in a linear fashion, up the neck – note that the notes are shown by the fret marker dots, with only the b5 added at the 6th fret. -

Tuning Forks As Time Travel Machines: Pitch Standardisation and Historicism for ”Sonic Things”: Special Issue of Sound Studies Fanny Gribenski
Tuning forks as time travel machines: Pitch standardisation and historicism For ”Sonic Things”: Special issue of Sound Studies Fanny Gribenski To cite this version: Fanny Gribenski. Tuning forks as time travel machines: Pitch standardisation and historicism For ”Sonic Things”: Special issue of Sound Studies. Sound Studies: An Interdisciplinary Journal, Taylor & Francis Online, 2020. hal-03005009 HAL Id: hal-03005009 https://hal.archives-ouvertes.fr/hal-03005009 Submitted on 13 Nov 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Tuning forks as time travel machines: Pitch standardisation and historicism Fanny Gribenski CNRS / IRCAM, Paris For “Sonic Things”: Special issue of Sound Studies Biographical note: Fanny Gribenski is a Research Scholar at the Centre National de la Recherche Scientifique and IRCAM, in Paris. She studied musicology and history at the École Normale Supérieure of Lyon, the Paris Conservatory, and the École des hautes études en sciences sociales. She obtained her PhD in 2015 with a dissertation on the history of concert life in nineteenth-century French churches, which served as the basis for her first book, L’Église comme lieu de concert. Pratiques musicales et usages de l’espace (1830– 1905) (Arles: Actes Sud / Palazzetto Bru Zane, 2019). -

Helmholtz's Dissonance Curve
Tuning and Timbre: A Perceptual Synthesis Bill Sethares IDEA: Exploit psychoacoustic studies on the perception of consonance and dissonance. The talk begins by showing how to build a device that can measure the “sensory” consonance and/or dissonance of a sound in its musical context. Such a “dissonance meter” has implications in music theory, in synthesizer design, in the con- struction of musical scales and tunings, and in the design of musical instruments. ...the legacy of Helmholtz continues... 1 Some Observations. Why do we tune our instruments the way we do? Some tunings are easier to play in than others. Some timbres work well in certain scales, but not in others. What makes a sound easy in 19-tet but hard in 10-tet? “The timbre of an instrument strongly affects what tuning and scale sound best on that instrument.” – W. Carlos 2 What are Tuning and Timbre? 196 384 589 amplitude 787 magnitude sample: 0 10000 20000 30000 0 1000 2000 3000 4000 time: 0 0.23 0.45 0.68 frequency in Hz Tuning = pitch of the fundamental (in this case 196 Hz) Timbre involves (a) pattern of overtones (Helmholtz) (b) temporal features 3 Some intervals “harmonious” and others “discordant.” Why? X X X X 1.06:1 2:1 X X X X 1.89:1 3:2 X X X X 1.414:1 4:3 4 Theory #1:(Pythagoras ) Humans naturally like the sound of intervals de- fined by small integer ratios. small ratios imply short period of repetition short = simple = sweet Theory #2:(Helmholtz ) Partials of a sound that are close in frequency cause beats that are perceived as “roughness” or dissonance. -

Pedagogical Practices Related to the Ability to Discern and Correct
Florida State University Libraries Electronic Theses, Treatises and Dissertations The Graduate School 2014 Pedagogical Practices Related to the Ability to Discern and Correct Intonation Errors: An Evaluation of Current Practices, Expectations, and a Model for Instruction Ryan Vincent Scherber Follow this and additional works at the FSU Digital Library. For more information, please contact [email protected] FLORIDA STATE UNIVERSITY COLLEGE OF MUSIC PEDAGOGICAL PRACTICES RELATED TO THE ABILITY TO DISCERN AND CORRECT INTONATION ERRORS: AN EVALUATION OF CURRENT PRACTICES, EXPECTATIONS, AND A MODEL FOR INSTRUCTION By RYAN VINCENT SCHERBER A Dissertation submitted to the College of Music in partial fulfillment of the requirements for the degree of Doctor of Philosophy Degree Awarded: Summer Semester, 2014 Ryan V. Scherber defended this dissertation on June 18, 2014. The members of the supervisory committee were: William Fredrickson Professor Directing Dissertation Alexander Jimenez University Representative John Geringer Committee Member Patrick Dunnigan Committee Member Clifford Madsen Committee Member The Graduate School has verified and approved the above-named committee members, and certifies that the dissertation has been approved in accordance with university requirements. ii For Mary Scherber, a selfless individual to whom I owe much. iii ACKNOWLEDGEMENTS The completion of this journey would not have been possible without the care and support of my family, mentors, colleagues, and friends. Your support and encouragement have proven invaluable throughout this process and I feel privileged to have earned your kindness and assistance. To Dr. William Fredrickson, I extend my deepest and most sincere gratitude. You have been a remarkable inspiration during my time at FSU and I will be eternally thankful for the opportunity to have worked closely with you. -

Musical Modes, Their Associated Chords and Their Musicality 3
MUSICAL MODES, THEIR ASSOCIATED CHORDS AND THEIR MUSICALITY MIHAIL COCOS & KENT KIDMAN Abstract. In this paper we present a mathematical way of defining musical modes and we define the musicality of a mode as a product of three differ- ent factors. We conclude by classifying the modes which are most musical according to our definition. 1. Musical scales and modes First we must define some concepts. In traditional western style of music there are 12 different notes in an octave. Two notes represent the same tone if they are at a distance of 12n semitones (a multiple of octaves apart). The 13th note restarts the cycle and it is the same tone as our first note (simply an octave higher). Loosely speaking a scale is simply an ordered sequence of different tones within the same octave. For instance CDEFGAB is the well known C major scale, ABCDEFG is the A minor scale, and EGAA#BD is the hexatonic blues scale in the key of E. The first note of the scale is said to be the key of the scale. Definition 1.1. For further considerations about scales we will associate every tone with a numerical value, namely its position in the chromatic A scale AA#BCC#CDD#EF F #GG# The lexicographic order of tones will be defined as the order induced by their nu- merical values defined as above. The precise mathematical definition of a scale is: arXiv:1201.2654v1 [math.CO] 12 Jan 2012 Definition 1.2. A k scale is a circular permutation of k different tones in lexico- graphic order.