Combining Old-Fashioned Computer Go with Monte Carlo Go
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Openbsd Gaming Resource
OPENBSD GAMING RESOURCE A continually updated resource for playing video games on OpenBSD. Mr. Satterly Updated August 7, 2021 P11U17A3B8 III Title: OpenBSD Gaming Resource Author: Mr. Satterly Publisher: Mr. Satterly Date: Updated August 7, 2021 Copyright: Creative Commons Zero 1.0 Universal Email: [email protected] Website: https://MrSatterly.com/ Contents 1 Introduction1 2 Ways to play the games2 2.1 Base system........................ 2 2.2 Ports/Editors........................ 3 2.3 Ports/Emulators...................... 3 Arcade emulation..................... 4 Computer emulation................... 4 Game console emulation................. 4 Operating system emulation .............. 7 2.4 Ports/Games........................ 8 Game engines....................... 8 Interactive fiction..................... 9 2.5 Ports/Math......................... 10 2.6 Ports/Net.......................... 10 2.7 Ports/Shells ........................ 12 2.8 Ports/WWW ........................ 12 3 Notable games 14 3.1 Free games ........................ 14 A-I.............................. 14 J-R.............................. 22 S-Z.............................. 26 3.2 Non-free games...................... 31 4 Getting the games 33 4.1 Games............................ 33 5 Former ways to play games 37 6 What next? 38 Appendices 39 A Clones, models, and variants 39 Index 51 IV 1 Introduction I use this document to help organize my thoughts, files, and links on how to play games on OpenBSD. It helps me to remember what I have gone through while finding new games. The biggest reason to read or at least skim this document is because how can you search for something you do not know exists? I will show you ways to play games, what free and non-free games are available, and give links to help you get started on downloading them. -

DVD-Libre 2005-04 Y 2 Pr W W Pr B - 3 T T T T S De Ca SI 5 Sc Re Ra Q 1 Po 3 Ph I Sa Dic Dic 2 4 W Ex ( H N C T
(continuación) - CDCheck 3.1.4.0 - CDex 1.51 - Celestia 1.3.2 - Centarsia 1.3 - Chain Reaction - Check4me 2.03 - Checky 2.5 - Chomp 1.4.5 - ClamWin 0.83 - Clan Bomber 1.05 - Cobian Backup 6.1.1.264 - Cobian Internet Tools 1.0.0.10 - ColorCop 5.3 - ColorWiz 1.0 - Combinaisons Junior Plus 2.70 - Continental 2.1 - Crack Attack! 1.1.08 - Crimson Editor 3.70 - CubeTest 0.9.3 - DBDesigner 4.0.5.6 - DeepBurner 1.3.6.168 - Deslizzzp 3.3 - Dev-C++ 4.9.9.2 - Dia Win32 0.94 - DirGraph 2.0 - DVD-Libre Disk Imager 1.4 - Domino Puzzle 0.1a - DominOSA 1.71 - DomiSol 1.2 - Doxygen 1.4.1 - Dragonboard 0.8c - Drawing for children 2.0 - DVD Identifier 3.6.2 - e-Counter 3.1.2004 - EasyISO 1.3 - EasyPHP cdlibre.org 1.8 - Eclipse 3.0.1 - Eclipse Language Pack 3.0.x - Eclipse Modeling Framework 2.0.1 - Eclipse Visual Editor 1.0.2 - Emilia Pinball 0.30c - Enigma 0.81 - EQTabla 4.0.050208 - Eraser 5.7 - Everest 2005-04 Dictionary 3.10 beta - Everest Dictionary 3.10 beta Completo - Exact Audio Copy 0.95 prebeta 5 - Exodus 0.9.0.0 - Fall - FileMenu Tools 4.1 - FileZilla 2.2.12a - Find Favorites 1.11 - Firebird 1.5.2 - Flexible Renamer 7.3 - FloboPuyo 0.20 - FolderQuote 1.0 - foobar2000 0.8.3 - FooBilliard 3.0 - Foxit PDF Reader 1.2.0.115 - FractalExplorer 2.02 - FractalForge 2.8.2 - FrameFun 1.0.5.0 - Free Download DVD-Libre es una recopilación de programas para Windows: Manager 1.5.256 - Free Pascal 1.0.10 - FreeCiv 1.14.2 - FreeMind 0.7.1 - Frozen Bubble Enhanced ● libres / gratuitos al menos para uso personal o educativo 1.0 - Gaim 1.1.4 - GanttProject 1.10.3 -

Walnut Creek CDROM Spring 1995 Catalog 1-800-786-9907 • 1-510-674-0821 Fax the Best of Walnut Creek CDROM Is Yours Free*
Walnut Creek CDROM Spring 1995 Catalog 1-800-786-9907 • 1-510-674-0821 Fax The Best of Walnut Creek CDROM is yours Free*. The • You’ll also get fonts, fractals, Best of Walnut Creek CDROM music, clipart, and more. 600 lets you explore in-depth what MegaBytes in total! Walnut Creek CDROM has to offer. • Boot images from our Unix for PC discs so you will With samples from all of our know if your hardware will products, you’ll be able to see boot Slackware Linux or what our CDROM’s will do for FreeBSD you, before you buy. This CDROM contains: • The Walnut Creek CDROM digital catalog - photos and • Index listings of all the descriptions of our all titles programs, photos, and files on all Walnut Creek CDROM If you act now, we’ll include titles $5.00 good toward the purchase of all Walnut Creek CDROM • The best from each disc titles. If you’re only going to including Hobbes OS/2, own one CDROM, this should CICA MS Windows, Simtel be it! March, 1995. MSDOS, Giga Games, Internet Info, Teacher 2000, Call, write, fax, or email your Ultra Mac-Games and Ultra order to us today! Mac-Utilities * The disc is without cost, but the regular shipping charge still applies. • You get applications, games, utilities, photos, gifs, documents, ray-tracings, and animations 2 CALL NOW! 1-800-786-9907 Phone: +1-510-674-0783 • Fax: +1-510-674-0821 • Email: [email protected] • WWW: http://WWW.cdrom.com/ (Alphabetical Index on page 39.) Hi, Sampler - (Best of Walnut Creek) 2 This is Jack and I’ve got another great batch of CICA for Windows 4 Music Workshop 5 CDROM’s for you. -

GHDL Documentation Release 1.0-Dev
GHDL Documentation Release 1.0-dev Tristan Gingold and contributors Aug 30, 2020 Introduction 1 What is VHDL? 3 2 What is GHDL? 5 3 Who uses GHDL? 7 4 Contributing 9 4.1 Reporting bugs............................................9 4.2 Requesting enhancements...................................... 10 4.3 Improving the documentation.................................... 10 4.4 Fork, modify and pull-request.................................... 11 4.5 Related interesting projects..................................... 11 5 Copyrights | Licenses 13 5.1 GNU GPLv2............................................. 13 5.2 CC-BY-SA.............................................. 14 5.3 List of Contributors......................................... 14 I Getting GHDL 15 6 Releases and sources 17 6.1 Using package managers....................................... 17 6.2 Downloading pre-built packages................................... 17 6.3 Downloading Source Files...................................... 18 7 Building GHDL from Sources 21 7.1 Directory structure.......................................... 22 7.2 mcode backend............................................ 23 7.3 LLVM backend............................................ 23 7.4 GCC backend............................................. 24 8 Precompile Vendor Primitives 27 8.1 Supported Vendors Libraries..................................... 27 8.2 Supported Simulation and Verification Libraries.......................... 28 8.3 Script Configuration......................................... 28 8.4 Compiling on Linux........................................ -

FUEGO – an Open-Source Framework for Board Games and Go Engine Based on Monte-Carlo Tree Search
FUEGO – An Open-source Framework for Board Games and Go Engine Based on Monte-Carlo Tree Search Markus Enzenberger, Martin Muller,¨ Broderick Arneson and Richard Segal Abstract—FUEGO is both an open-source software frame- available source code such as Hoffmann’s FF [20] have had work and a state of the art program that plays the game of a similarly massive impact, and have enabled much followup Go. The framework supports developing game engines for full- research. information two-player board games, and is used successfully in UEGO a substantial number of projects. The FUEGO Go program be- F contains a game-independent, state of the art came the first program to win a game against a top professional implementation of MCTS with many standard enhancements. player in 9×9 Go. It has won a number of strong tournaments It implements a coherent design, consistent with software against other programs, and is competitive for 19 × 19 as well. engineering best practices. Advanced features include a lock- This paper gives an overview of the development and free shared memory architecture, and a flexible and general current state of the FUEGO project. It describes the reusable components of the software framework and specific algorithms plug-in architecture for adding domain-specific knowledge in used in the Go engine. the game tree. The FUEGO framework has been proven in applications to Go, Hex, Havannah and Amazons. I. INTRODUCTION The main innovation of the overall FUEGO framework may lie not in the novelty of any of its specific methods and Research in computing science is driven by the interplay algorithms, but in the fact that for the first time, a state of of theory and practice. -

Advanced Optimization and New Capabilities of GCC 10
SUSE Best Practices Advanced Optimization and New Capabilities of GCC 10 Development Tools Module, SUSE Linux Enterprise 15 SP2 Martin Jambor, Toolchain Developer, SUSE Jan Hubička, Toolchain Developer, SUSE Richard Biener, Toolchain Developer, SUSE Martin Liška, Toolchain Developer, SUSE Michael Matz, Toolchain Team Lead, SUSE Brent Hollingsworth, Engineering Manager, AMD 1 Advanced Optimization and New Capabilities of GCC 10 The document at hand provides an overview of GCC 10 as the current Development Tools Module compiler in SUSE Linux Enterprise 15 SP2. It focuses on the important optimization levels and options Link Time Optimization (LTO) and Prole Guided Optimization (PGO). Their eects are demonstrated by compiling the SPEC CPU benchmark suite for AMD EPYC 7002 Series Processors and building Mozilla Firefox for a generic x86_64 machine. Disclaimer: This document is part of the SUSE Best Practices series. All documents published in this series were contributed voluntarily by SUSE employees and by third parties. If not stated otherwise inside the document, the articles are intended only to be one example of how a particular action could be taken. Also, SUSE cannot verify either that the actions described in the articles do what they claim to do or that they do not have unintended consequences. All information found in this document has been compiled with utmost attention to detail. However, this does not guarantee complete accuracy. Therefore, we need to specically state that neither SUSE LLC, its aliates, the authors, nor the translators -

Enhancing a Tactical Framework for Go Using Monte Carlo Statistics
Enhancing a Tactical Framework for Go Using Monte Carlo Statistics Niclas P˚alsson February 18, 2008 Examensarbete f¨or20 p, Institutionen f¨orDatavetenskap, Lunds Tekniska H¨ogskola Master’s thesis for a diploma in computer science, 20 credit points, Department of Computer Science, Lund Institute of Technology Abstract Go is an ancient board game based on surrounding territory by placing stones on a grid. It has proven very difficult to create computer programs that play the game well. Monte Carlo statistics has in recent years been a popular subject of research for creating computer programs playing Go. It relies very little on domain specific knowledge, and therefore presents an alternative to knowledge based Go, which is difficult to improve. Furthermore it doesn’t suffer from the drawbacks associated with tree search in games with high branching factors such as Go. However, programs relying solely on Monte Carlo methods are still inferior to good knowledge based programs such as GNU Go. The object of study for this thesis is whether it’s possible to create synergy by integrating a Monte Carlo module into the tactical framework of GNU Go, for Go played on a 9x9 board. Four different strategies are tested for integrating the module, and for each one the degree of Monte Carlo influence is parameterised and varied to empirically find the optimal level. Two simple Monte Carlo models are tested: the Abramson’s Expected Outcome heuristic, and a simplified version of Br¨ugmann’s model from Gobble, the first Go program to use Monte Carlo methods. The study shows that it’s possible to improve the playing strength of GNU Go 3.6 so that it wins a statistically significant greater proportion of games played against the unmodified program, and the best integration strategy is identified for doing so. -

DVD-Libre 2005-05 Y X S W W 2 W W V K T T T T P Do - 0 S E Ro Re 1 Ca P P 3 Ca P P Org - 0 Ne M V (C H X
(continuación) - ColorCop 5.3 - ColorWiz 1.0 - Combinaisons Junior Plus 2.70 - Continental 2.1 - Crack Attack! 1.1.08 - Crimson Editor 3.70 - CubeTest 0.9.3 - DBDesigner 4.0.5.6 - DeepBurner 1.5.1.192 - Deluxe Snake 3.8.1 - Deslizzzp 3.3 - Dev-C++ 4.9.9.2 - Dia Win32 0.94 - DirGraph 2.0 - Disk Imager 1.4 - DjVu Browser Plug-in 5.0.1 - Domino Puzzle 0.1a - DominOSA 1.71 - DomiSol 1.2 - Doxygen DVD-Libre 1.4.2 - Dragonboard 0.8c - Drawing for children 2.0 - Drupal 4.6.0 - DVD Identifier 3.6.3.1 - e-Counter 3.2.2005 - EasyISO 1.3 - EasyPHP 1.8 - Eclipse 3.0.2 - Eclipse Language Pack 3.0.x - Eclipse cdlibre.org Modeling Framework 2.0.1 - Eclipse Visual Editor 1.0.2 - Emilia Pinball 0.30c - Enigma 0.9.1 - EQTabla 4.0.050208 - Eraser 5.7 - Everest Dictionary 3.10 beta + Completo - Exact Audio Copy 0.95 2005-05 beta 1 - Exodus 0.9.1.0 - Fall - FileMenu Tools 4.1 - FileZilla 2.2.13c - FileZilla Server 0.9.7 - Find Favorites 1.11 - Firebird 1.5.2 - Flexible Renamer 7.3 - FlightGear 0.9.8a - FloboPuyo 0.20 - DVD-Libre es una recopilación de programas para Windows: FolderQuote 1.0 - foobar2000 0.8.3 - FooBilliard 3.0 - Foxit PDF Reader 1.3.0504 - FractalExplorer ● libres / gratuitos al menos para uso personal o educativo 2.02 - FractalForge 2.8.2 - FrameFun 1.0.5.0 - Free Download Manager 1.7.286 + Castellano - Free ● Pascal 1.0.10 - Free SMTP Server 2.1 - FreeCiv 2.0.1 - FreeDOS 0.9 SR1 CD - FreeDOS 0.9 SR1 sin limitaciones temporales Disquete de arranque - Freedroid Classic 1.0.2 + biblioteca SDL - FreeMind 0.7.1 - Frozen Bubble Enhanced 1.0 - Gaim 1.3.0 - GanttProject 1.11 - Gem Drop X 0.9 - GenoPro 1.91b - Geonext 1.11 - En http://www.cdlibre.org puedes conseguir la versión más actual de este GIMP 2.2.3 Catalán - GIMP 2.2.7 - GIMP Animation package 2.0.2 - Glace 1.2 - GLtron 0.7 - GNU DVD, así como otros CDs recopilatorios de programas y fuentes. -

SPEC CPU2006 Benchmark Descriptions
SPEC CPU2006 Benchmark Descriptions Descriptions written by the SPEC CPU Subcommittee and by the original program authors [1]. Edited by John L. Henning, Secretary, SPEC CPU Subcommittee, and Performance Engineer, Sun Microsystems. Contact [email protected] Introduction tions, rather than using artificial loop kernels or synthetic benchmarks. Therefore, the most important parts of the new On August 24, 2006, the Standard Performance Evalua- suite are the benchmarks themselves, which are described on tion Corporation (SPEC) announced CPU2006 [2], which re- the pages that follow. In a future issue of Computer Architec- places CPU2000. The SPEC CPU benchmarks are widely used ture News, information will be provided about other aspects of in both industry and academia [3]. the new suite, including additional technical detail regarding The new suite is much larger than the previous, and will benchmark behavior and profiles. exercise new corners of CPUs, memory systems, and compil- ers – especially C++ compilers. Where CPU2000 had only 1 References: benchmark in C++, the new suite has 7, including one with ½ [1] Program authors are listed in the descriptions below, million lines of C++ code. As in previous CPU suites, Fortran which are adapted from longer versions posted at and C are also well represented. www.spec.org/cpu2006/Docs/. The SPEC project leaders Since its beginning, SPEC has claimed the motto that are listed in credits.html at the same location. [2] SPEC’s press announcement may be found at “An ounce of honest data www.spec.org/cpu2006/press/release.html is worth a pound of marketing hype”. [3] SPEC’s website has over 6000 published results for CPU2000, at www.spec.org/cpu2000/results. -

What Is the Project Title
Artificial Intelligence for Go CIS 499 Senior Design Project Final Report Kristen Ying Advisors: Dr. Badler and Dr. Likhachev University of Pennsylvania PROJECT ABSTRACT Go is an ancient board game, originating in China – where it is known as weiqi - before 600 B.C. It spread to Japan (where it is also known as Go), to Korea as baduk, and much more recently to Europe and America [American Go Association]. This game, in which players take turn placing stones on a 19x19 board in an attempt to capture territory, is polynomial-space hard [Reyzin]. Checkers is also polynomial-space hard, and is a solved problem [Schaeffer]. However, the sheer magnitude of options (and for intelligent algorithms, sheer number of possible strategies) makes it infeasible to create even passable novice AI with an exhaustive pure brute-force approach on modern hardware. The board is 19 x19, which, barring illegal moves, allows for about 10171 possible ways to execute a game. This number is about 1081 times greater than the believed number of elementary particles contained in the known universe [Keim]. Previously investigated approaches to creating AI for Go include human-like models such as pattern recognizers and machine learning [Burmeister and Wiles]. There are a number of challenges to these approaches, however. Machine learning algorithms can be very sensitive to the data and style of play with which they are trained, and approaches modeling human thought can be very sensitive to the designer‟s perception of how one thinks during a game. Professional Go players seem to have a very intuitive sense of how to play, which is difficult to model. -

GHDL Documentation Release 0.37-Dev Tristan Gingold
GHDL Documentation Release 0.37-dev Tristan Gingold Oct 12, 2019 Introduction 1 About GHDL 3 1.1 What is VHDL?............................................3 1.2 What is GHDL?...........................................3 1.3 Who uses GHDL?..........................................4 2 Contributing 5 2.1 Reporting bugs............................................5 2.2 Requesting enhancements......................................6 2.3 Improving the documentation....................................6 2.4 Fork, modify and pull-request....................................7 2.5 Related interesting projects.....................................7 3 Copyrights | Licenses 9 3.1 GNU GPLv2.............................................9 3.2 CC-BY-SA.............................................. 10 3.3 List of Contributors......................................... 10 I GHDL usage 11 4 Quick Start Guide 13 4.1 The ‘Hello world’ program..................................... 13 4.2 The heartbeat program........................................ 14 4.3 A full adder.............................................. 14 4.4 Starting with a design........................................ 16 4.5 Starting with your design....................................... 17 5 Invoking GHDL 19 5.1 Design building commands..................................... 19 5.2 Design rebuilding commands.................................... 21 5.3 Options................................................ 23 5.4 Warnings............................................... 24 5.5 Diagnostics Control........................................ -
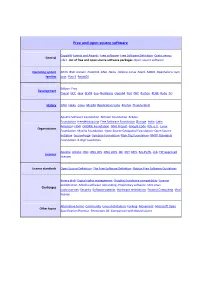
Free and Open Source Software
Free and open source software Copyleft ·Events and Awards ·Free software ·Free Software Definition ·Gratis versus General Libre ·List of free and open source software packages ·Open-source software Operating system AROS ·BSD ·Darwin ·FreeDOS ·GNU ·Haiku ·Inferno ·Linux ·Mach ·MINIX ·OpenSolaris ·Sym families bian ·Plan 9 ·ReactOS Eclipse ·Free Development Pascal ·GCC ·Java ·LLVM ·Lua ·NetBeans ·Open64 ·Perl ·PHP ·Python ·ROSE ·Ruby ·Tcl History GNU ·Haiku ·Linux ·Mozilla (Application Suite ·Firefox ·Thunderbird ) Apache Software Foundation ·Blender Foundation ·Eclipse Foundation ·freedesktop.org ·Free Software Foundation (Europe ·India ·Latin America ) ·FSMI ·GNOME Foundation ·GNU Project ·Google Code ·KDE e.V. ·Linux Organizations Foundation ·Mozilla Foundation ·Open Source Geospatial Foundation ·Open Source Initiative ·SourceForge ·Symbian Foundation ·Xiph.Org Foundation ·XMPP Standards Foundation ·X.Org Foundation Apache ·Artistic ·BSD ·GNU GPL ·GNU LGPL ·ISC ·MIT ·MPL ·Ms-PL/RL ·zlib ·FSF approved Licences licenses License standards Open Source Definition ·The Free Software Definition ·Debian Free Software Guidelines Binary blob ·Digital rights management ·Graphics hardware compatibility ·License proliferation ·Mozilla software rebranding ·Proprietary software ·SCO-Linux Challenges controversies ·Security ·Software patents ·Hardware restrictions ·Trusted Computing ·Viral license Alternative terms ·Community ·Linux distribution ·Forking ·Movement ·Microsoft Open Other topics Specification Promise ·Revolution OS ·Comparison with closed