Causal Gene Inference by Multivariate Mediation Analysis in Alzheimer's Disease
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Computational Approach for Defining a Signature of Β-Cell Golgi Stress in Diabetes Mellitus
Page 1 of 781 Diabetes A Computational Approach for Defining a Signature of β-Cell Golgi Stress in Diabetes Mellitus Robert N. Bone1,6,7, Olufunmilola Oyebamiji2, Sayali Talware2, Sharmila Selvaraj2, Preethi Krishnan3,6, Farooq Syed1,6,7, Huanmei Wu2, Carmella Evans-Molina 1,3,4,5,6,7,8* Departments of 1Pediatrics, 3Medicine, 4Anatomy, Cell Biology & Physiology, 5Biochemistry & Molecular Biology, the 6Center for Diabetes & Metabolic Diseases, and the 7Herman B. Wells Center for Pediatric Research, Indiana University School of Medicine, Indianapolis, IN 46202; 2Department of BioHealth Informatics, Indiana University-Purdue University Indianapolis, Indianapolis, IN, 46202; 8Roudebush VA Medical Center, Indianapolis, IN 46202. *Corresponding Author(s): Carmella Evans-Molina, MD, PhD ([email protected]) Indiana University School of Medicine, 635 Barnhill Drive, MS 2031A, Indianapolis, IN 46202, Telephone: (317) 274-4145, Fax (317) 274-4107 Running Title: Golgi Stress Response in Diabetes Word Count: 4358 Number of Figures: 6 Keywords: Golgi apparatus stress, Islets, β cell, Type 1 diabetes, Type 2 diabetes 1 Diabetes Publish Ahead of Print, published online August 20, 2020 Diabetes Page 2 of 781 ABSTRACT The Golgi apparatus (GA) is an important site of insulin processing and granule maturation, but whether GA organelle dysfunction and GA stress are present in the diabetic β-cell has not been tested. We utilized an informatics-based approach to develop a transcriptional signature of β-cell GA stress using existing RNA sequencing and microarray datasets generated using human islets from donors with diabetes and islets where type 1(T1D) and type 2 diabetes (T2D) had been modeled ex vivo. To narrow our results to GA-specific genes, we applied a filter set of 1,030 genes accepted as GA associated. -

4-6 Weeks Old Female C57BL/6 Mice Obtained from Jackson Labs Were Used for Cell Isolation
Methods Mice: 4-6 weeks old female C57BL/6 mice obtained from Jackson labs were used for cell isolation. Female Foxp3-IRES-GFP reporter mice (1), backcrossed to B6/C57 background for 10 generations, were used for the isolation of naïve CD4 and naïve CD8 cells for the RNAseq experiments. The mice were housed in pathogen-free animal facility in the La Jolla Institute for Allergy and Immunology and were used according to protocols approved by the Institutional Animal Care and use Committee. Preparation of cells: Subsets of thymocytes were isolated by cell sorting as previously described (2), after cell surface staining using CD4 (GK1.5), CD8 (53-6.7), CD3ε (145- 2C11), CD24 (M1/69) (all from Biolegend). DP cells: CD4+CD8 int/hi; CD4 SP cells: CD4CD3 hi, CD24 int/lo; CD8 SP cells: CD8 int/hi CD4 CD3 hi, CD24 int/lo (Fig S2). Peripheral subsets were isolated after pooling spleen and lymph nodes. T cells were enriched by negative isolation using Dynabeads (Dynabeads untouched mouse T cells, 11413D, Invitrogen). After surface staining for CD4 (GK1.5), CD8 (53-6.7), CD62L (MEL-14), CD25 (PC61) and CD44 (IM7), naïve CD4+CD62L hiCD25-CD44lo and naïve CD8+CD62L hiCD25-CD44lo were obtained by sorting (BD FACS Aria). Additionally, for the RNAseq experiments, CD4 and CD8 naïve cells were isolated by sorting T cells from the Foxp3- IRES-GFP mice: CD4+CD62LhiCD25–CD44lo GFP(FOXP3)– and CD8+CD62LhiCD25– CD44lo GFP(FOXP3)– (antibodies were from Biolegend). In some cases, naïve CD4 cells were cultured in vitro under Th1 or Th2 polarizing conditions (3, 4). -

A Bayesian Approach to Mediation Analysis Predicts 206 Causal Target Genes in Alzheimer’S Disease
bioRxiv preprint first posted online Nov. 14, 2017; doi: http://dx.doi.org/10.1101/219428. The copyright holder for this preprint (which was not peer-reviewed) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. All rights reserved. No reuse allowed without permission. Title A Bayesian approach to mediation analysis predicts 206 causal target genes in Alzheimer’s disease Authors Yongjin Park+;1;2, Abhishek K Sarkar+;3, Liang He+;1;2, Jose Davila-Velderrain1;2, Philip L De Jager2;4, Manolis Kellis1;2 +: equal contribution. 1: Computer Science and Artificial Intelligence Laboratory, Massachusetts Institute of Technology, Cambridge, MA, USA 2: Broad Institute of MIT and Harvard, Cambridge, MA, USA 3: Department of Human Genetics, University of Chicago, Chicago, IL, USA 4: Department of Neurology, Columbia University Medical Center, New York, NY, USA MK: [email protected] Abstract Characterizing the intermediate phenotypes, such as gene expression, that mediate genetic effects on complex dis- eases is a fundamental problem in human genetics. Existing methods utilize genotypic data and summary statistics to identify putative disease genes, but cannot distinguish pleiotropy from causal mediation and are limited by overly strong assumptions about the data. To overcome these limitations, we develop Causal Multivariate Mediation within Extended Linkage disequilibrium (CaMMEL), a novel Bayesian inference framework to jointly model multiple medi- ated and unmediated effects relying only on summary statistics. We show in simulation that CaMMEL accurately distinguishes between mediating and pleiotropic genes unlike existing methods. We applied CaMMEL to Alzheimer’s disease (AD) and found 206 causal genes in sub-threshold loci (p < 10−4). -

Chloride Channels Regulate Differentiation and Barrier Functions
RESEARCH ARTICLE Chloride channels regulate differentiation and barrier functions of the mammalian airway Mu He1†*, Bing Wu2†, Wenlei Ye1, Daniel D Le2, Adriane W Sinclair3,4, Valeria Padovano5, Yuzhang Chen6, Ke-Xin Li1, Rene Sit2, Michelle Tan2, Michael J Caplan5, Norma Neff2, Yuh Nung Jan1,7,8, Spyros Darmanis2*, Lily Yeh Jan1,7,8* 1Department of Physiology, University of California, San Francisco, San Francisco, United States; 2Chan Zuckerberg Biohub, San Francisco, United States; 3Department of Urology, University of California, San Francisco, San Francisco, United States; 4Division of Pediatric Urology, University of California, San Francisco, Benioff Children’s Hospital, San Francisco, United States; 5Department of Cellular and Molecular Physiology, Yale University School of Medicine, New Heaven, United States; 6Department of Anesthesia and Perioperative Care, University of California, San Francisco, San Francisco, United States; 7Department of Biochemistry and Biophysics, University of California, San Francisco, San Francisco, United States; 8Howard Hughes Medical Institute, University of California, San Francisco, San Francisco, United States *For correspondence: Abstract The conducting airway forms a protective mucosal barrier and is the primary target of [email protected] (MH); [email protected] airway disorders. The molecular events required for the formation and function of the airway (SD); mucosal barrier, as well as the mechanisms by which barrier dysfunction leads to early onset airway [email protected] (LYJ) diseases, -

Chicken Linkage Disequilibrium Is Much More Complex Over Much Longer Distance Than Previously Appreciated
Look Over the Horizon - Chicken Linkage Disequilibrium is Much More Complex Over Much Longer Distance than Previously Appreciated Ehud Lipkin ( [email protected] ) Hebrew University of Jerusalem Janet E. Fulton Hy-Line (United States) Jacqueline Smith University of Edinburgh David W. Burt University of Edinburgh Morris Soller Hebrew University of Jerusalem Research Article Keywords: Chicken, long-range linkage disequilibrium, QTL, F6, LD blocks Posted Date: June 17th, 2021 DOI: https://doi.org/10.21203/rs.3.rs-598396/v1 License: This work is licensed under a Creative Commons Attribution 4.0 International License. Read Full License Page 1/23 Abstract Background Appreciable Linkage Disequilibrium (LD) is commonly found between pairs of loci close to one another, decreasing rapidly with distance between the loci. This provides the basis studies to map Quantitative Trait Loci Regions (QTLRs), where it is custom to assume that the closest sites to a signicant markers are the prime candidate to be the causative mutation. Nevertheless, Long-Range LD (LRLD) can also be found among well-separated sites. LD blocks are runs of genomic sites all having appreciable LD with one another. High LD and LRLD are often separated by genomic sites with which they have practically no LD. Thus, not only can LD be found among distant loci, but also its pattern may be complex, comprised of fragmented blocks. Here, chicken LRLD and LD blocks, and their relationship with previously described Marek’s Disease (MD) QTLRs, were studied in an F6 population from a full-sib advanced intercross line, and in eight commercial pure layer lines. -

Human Induced Pluripotent Stem Cell–Derived Podocytes Mature Into Vascularized Glomeruli Upon Experimental Transplantation
BASIC RESEARCH www.jasn.org Human Induced Pluripotent Stem Cell–Derived Podocytes Mature into Vascularized Glomeruli upon Experimental Transplantation † Sazia Sharmin,* Atsuhiro Taguchi,* Yusuke Kaku,* Yasuhiro Yoshimura,* Tomoko Ohmori,* ‡ † ‡ Tetsushi Sakuma, Masashi Mukoyama, Takashi Yamamoto, Hidetake Kurihara,§ and | Ryuichi Nishinakamura* *Department of Kidney Development, Institute of Molecular Embryology and Genetics, and †Department of Nephrology, Faculty of Life Sciences, Kumamoto University, Kumamoto, Japan; ‡Department of Mathematical and Life Sciences, Graduate School of Science, Hiroshima University, Hiroshima, Japan; §Division of Anatomy, Juntendo University School of Medicine, Tokyo, Japan; and |Japan Science and Technology Agency, CREST, Kumamoto, Japan ABSTRACT Glomerular podocytes express proteins, such as nephrin, that constitute the slit diaphragm, thereby contributing to the filtration process in the kidney. Glomerular development has been analyzed mainly in mice, whereas analysis of human kidney development has been minimal because of limited access to embryonic kidneys. We previously reported the induction of three-dimensional primordial glomeruli from human induced pluripotent stem (iPS) cells. Here, using transcription activator–like effector nuclease-mediated homologous recombination, we generated human iPS cell lines that express green fluorescent protein (GFP) in the NPHS1 locus, which encodes nephrin, and we show that GFP expression facilitated accurate visualization of nephrin-positive podocyte formation in -

Learning Gene Networks Underlying Clinical Phenotypes Under SNP Perturbations from Genome-Wide Data Calvin Mccarter
May 23, 2019 DRAFT Learning Gene Networks Underlying Clinical Phenotypes Under SNP Perturbations From Genome-Wide Data Calvin McCarter May 2019 School of Computer Science Carnegie Mellon University Pittsburgh, PA 15213 Thesis Committee: Seyoung Kim, Chair Pradeep Ravikumar Kathryn Roeder Dietrich Stephan (NeuBase Therapeutics, previously The University of Pittsburgh) Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy. Copyright c 2019 Calvin McCarter May 23, 2019 DRAFT Keywords: probabilistic graphical models, sparse learning, structure learning, convex opti- mization, genomics, gene networks, systems biology May 23, 2019 DRAFT When thou shalt do wonderful things, we shall not bear them: thou didst come down, and at thy presence the mountains melted away. From the beginning of the world they have not heard, nor perceived with the ears: the eye hath not seen, O God, besides thee, what things thou hast prepared for them that wait for thee. May 23, 2019 DRAFT iv May 23, 2019 DRAFT Abstract Recent technologies are generating an abundance of genome sequence data and molecular and clinical phenotype data, providing an opportunity to understand the genetic architecture and molecular mechanisms underlying diseases. Previous ap- proaches have largely focused on the co-localization of single-nucleotide polymor- phisms (SNPs) associated with clinical and expression traits, each identified from genome-wide association studies and expression quantitative trait locus (eQTL) map- ping, and thus have provided only limited capabilities for uncovering the molecular mechanisms behind the SNPs influencing clinical phenotypes. Here we aim to ex- tract rich information on the functional role of trait-perturbing SNPs that goes far beyond this simple co-localization. -

Causal Gene Inference by Multivariate Mediation Analysis in Alzheimer’S Disease
bioRxiv preprint doi: https://doi.org/10.1101/219428; this version posted November 14, 2017. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. Title Causal gene inference by multivariate mediation analysis in Alzheimer’s disease Authors and affiliations Yongjin Park+;1;2, Abhishek K Sarkar+;1;2;3, Liang He+;1;2, Jose Davilla-Velderrain1;2, Philip L De Jager2;4, Manolis Kellis1;2 +: equal contribution. 1: Computer Science and Artificial Intelligence Laboratory, Massachusetts Institute of Technology, Cambridge, MA, USA 2: Broad Institute of MIT and Harvard, Cambridge, MA, USA 3: Department of Human Genetics, University of Chicago, Chicago, IL, USA (current affiliation) 4: Department of Neurology, Columbia University Medical Center, New York, NY, USA YP: [email protected]; PLD: [email protected]; MK: [email protected] Abstract Characterizing the intermediate phenotypes such as gene expression that mediate genetic effects on complex dis- eases is a fundamental problem in human genetics. Existing methods based on imputation of transcriptomic data by utilizing genotypic data and summary statistics to identify putative disease genes cannot distinguish pleiotropy from causal mediation and are limited by overly strong assumptions about the data. To overcome these limitations, we develop a novel Bayesian inference framework, termed Causal Multivariate Mediation within Extended Linkage dise- quilibrium (CaMMEL), to jointly model multiple mediated and unmediated effects, relying only on summary statistics. We show in simulation unlike existing methods fail to distinguish between mediation and independent direct effects, CaMMEL accurately estimates mediation genes, clearly excluding pleiotropic genes. -

Content Based Search in Gene Expression Databases and a Meta-Analysis of Host Responses to Infection
Content Based Search in Gene Expression Databases and a Meta-analysis of Host Responses to Infection A Thesis Submitted to the Faculty of Drexel University by Francis X. Bell in partial fulfillment of the requirements for the degree of Doctor of Philosophy November 2015 c Copyright 2015 Francis X. Bell. All Rights Reserved. ii Acknowledgments I would like to acknowledge and thank my advisor, Dr. Ahmet Sacan. Without his advice, support, and patience I would not have been able to accomplish all that I have. I would also like to thank my committee members and the Biomed Faculty that have guided me. I would like to give a special thanks for the members of the bioinformatics lab, in particular the members of the Sacan lab: Rehman Qureshi, Daisy Heng Yang, April Chunyu Zhao, and Yiqian Zhou. Thank you for creating a pleasant and friendly environment in the lab. I give the members of my family my sincerest gratitude for all that they have done for me. I cannot begin to repay my parents for their sacrifices. I am eternally grateful for everything they have done. The support of my sisters and their encouragement gave me the strength to persevere to the end. iii Table of Contents LIST OF TABLES.......................................................................... vii LIST OF FIGURES ........................................................................ xiv ABSTRACT ................................................................................ xvii 1. A BRIEF INTRODUCTION TO GENE EXPRESSION............................. 1 1.1 Central Dogma of Molecular Biology........................................... 1 1.1.1 Basic Transfers .......................................................... 1 1.1.2 Uncommon Transfers ................................................... 3 1.2 Gene Expression ................................................................. 4 1.2.1 Estimating Gene Expression ............................................ 4 1.2.2 DNA Microarrays ...................................................... -

Supplementary Figure 1. Dystrophic Mice Show Unbalanced Stem Cell Niche
Supplementary Figure 1. Dystrophic mice show unbalanced stem cell niche. (A) Single channel images for the merged panels shown in Figure 1A, for of PAX7, MYOD and Laminin immunohistochemical staining in Lmna Δ8-11 mice of PAX7 and MYOD markers at the indicated days of post-natal growth. Basement membrane of muscle fibers was stained with Laminin. Scale bars, 50 µm. (B) Quantification of the % of PAX7+ MuSCs per 100 fibers at the indicated days of post-natal growth in (A). n =3-6 animals per genotype. (C) Immunohistochemical staining in Lmna Δ8-11 mice of activated, ASCs (PAX7+/KI67+) and quiescent QSCs (PAX7+/Ki67-) MuSCs at d19 and relative quantification (below). n= 4-6 animals per genotype. Scale bars, 50 µm. (D) Quantification of the number of cells per cluster in single myofibers extracted from d19 Lmna Δ8-11 mice and cultured 96h. n= 4-5 animals per group. Data are box with median and whiskers min to max. B, C, Data are mean ± s.e.m. Statistics by one-way (B) or two-way (C, D) analysis of variance (ANOVA) with multiple comparisons. * * P < 0.01, * * * P < 0.001. wt= Lmna Δ8-11 +/+; het= Lmna Δ8-11 +/; hom= Lmna Δ8-11 -/-. Supplementary Figure 2. Heterozygous mice show intermediate Lamin A levels. (A) RNA-seq signal tracks as the effective genome size normalized coverage of each biological replicate of Lmna Δ8-11 mice on Lmna locus. Neomycine cassette is indicated as a dark blue rectangle. (B) Western blot of total protein extracted from the whole Lmna Δ8-11 muscles at d19 hybridized with indicated antibodies. -

A Bayesian Approach to Mediation Analysis Predicts 206 Causal Target Genes in Alzheimer’S Disease
bioRxiv preprint doi: https://doi.org/10.1101/219428; this version posted December 1, 2017. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. Title A Bayesian approach to mediation analysis predicts 206 causal target genes in Alzheimer’s disease Authors Yongjin Park+;1;2, Abhishek K Sarkar+;3, Liang He+;1;2, Jose Davila-Velderrain1;2, Philip L De Jager2;4, Manolis Kellis1;2 +: equal contribution. 1: Computer Science and Artificial Intelligence Laboratory, Massachusetts Institute of Technology, Cambridge, MA, USA 2: Broad Institute of MIT and Harvard, Cambridge, MA, USA 3: Department of Human Genetics, University of Chicago, Chicago, IL, USA 4: Department of Neurology, Columbia University Medical Center, New York, NY, USA MK: [email protected] Abstract Characterizing the intermediate phenotypes, such as gene expression, that mediate genetic effects on complex dis- eases is a fundamental problem in human genetics. Existing methods utilize genotypic data and summary statistics to identify putative disease genes, but cannot distinguish pleiotropy from causal mediation and are limited by overly strong assumptions about the data. To overcome these limitations, we develop Causal Multivariate Mediation within Extended Linkage disequilibrium (CaMMEL), a novel Bayesian inference framework to jointly model multiple medi- ated and unmediated effects relying only on summary statistics. We show in simulation that CaMMEL accurately distinguishes between mediating and pleiotropic genes unlike existing methods. We applied CaMMEL to Alzheimer’s disease (AD) and found 206 causal genes in sub-threshold loci (p < 10−4). We prioritized 21 genes which mediate at least 5% of local genetic variance, disrupting innate immune pathways in AD. -
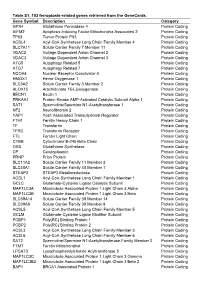
Table S1. 103 Ferroptosis-Related Genes Retrieved from the Genecards
Table S1. 103 ferroptosis-related genes retrieved from the GeneCards. Gene Symbol Description Category GPX4 Glutathione Peroxidase 4 Protein Coding AIFM2 Apoptosis Inducing Factor Mitochondria Associated 2 Protein Coding TP53 Tumor Protein P53 Protein Coding ACSL4 Acyl-CoA Synthetase Long Chain Family Member 4 Protein Coding SLC7A11 Solute Carrier Family 7 Member 11 Protein Coding VDAC2 Voltage Dependent Anion Channel 2 Protein Coding VDAC3 Voltage Dependent Anion Channel 3 Protein Coding ATG5 Autophagy Related 5 Protein Coding ATG7 Autophagy Related 7 Protein Coding NCOA4 Nuclear Receptor Coactivator 4 Protein Coding HMOX1 Heme Oxygenase 1 Protein Coding SLC3A2 Solute Carrier Family 3 Member 2 Protein Coding ALOX15 Arachidonate 15-Lipoxygenase Protein Coding BECN1 Beclin 1 Protein Coding PRKAA1 Protein Kinase AMP-Activated Catalytic Subunit Alpha 1 Protein Coding SAT1 Spermidine/Spermine N1-Acetyltransferase 1 Protein Coding NF2 Neurofibromin 2 Protein Coding YAP1 Yes1 Associated Transcriptional Regulator Protein Coding FTH1 Ferritin Heavy Chain 1 Protein Coding TF Transferrin Protein Coding TFRC Transferrin Receptor Protein Coding FTL Ferritin Light Chain Protein Coding CYBB Cytochrome B-245 Beta Chain Protein Coding GSS Glutathione Synthetase Protein Coding CP Ceruloplasmin Protein Coding PRNP Prion Protein Protein Coding SLC11A2 Solute Carrier Family 11 Member 2 Protein Coding SLC40A1 Solute Carrier Family 40 Member 1 Protein Coding STEAP3 STEAP3 Metalloreductase Protein Coding ACSL1 Acyl-CoA Synthetase Long Chain Family Member 1 Protein