DOCSLIB.ORG

Bayesian Determination of Disease Associated Differences in Haplotype Blocks

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Bayesian Determination of Disease Associated Differences in Haplotype Blocks American Journal of Bioinformatics 1 (1): 20-29, 2012 ISSN 1948-9862 © 2012 Science Publications Bayesian Determination of Disease Associated Differences in Haplotype Blocks 1Ivan Kozyryev and 2Jing Zhang 1Department of Physics, Faculty of Arts and Sciences, Harvard University, Cambridge, MA, USA 2Department of Statistics, Faculty of Arts and Sciences, Yale University, New Haven, CT, USA Abstract: Problem statement: While experimental ascertainment of haplotype blocks in the genome- scale case-control studies is expensive, accurate computational phasing is still a daunting task for bioinformatics approaches. We used a statistical method to determine differences, potentially associated with a certain disease, in linkage disequilibrium block boundaries in whole-genome Single Nucleotide Polymorphisms (SNPs) data. Approach: We utilized a Bayesian model for calculating the posterior probabilities of the block boundaries in the SNPs data and used Metropolis-Hastings algorithm to sample from that posterior distribution. Our method was applied to search for haplotype- block boundary differences associated with two autoimmune diseases: Type I Diabetes (T1D) and Rheumatoid Arthritis (RA). Results: We located the regions on chromosome 6 with significant control-case difference in haplotype blocks around the SNPs and genes that were previously known to be associated with T1D and RA (in the HLA complex), as well as around genes whose association with the autoimmune diseases should be further explored in future studies. Conclusion/Recommendations: The statistical approach explored in this study provides an efficient and accurate way to study connection of haplotype-block differences to multiple important diseases. Key words: Linkage disequilibrium, autoimmune diseases, HLA complex, type 1 diabetes, rheumatoid arthritis INTRODUCTION be thought of as “tiny typos” in the genome with one base being replaced by another. While some SNPs Statistical approaches in genetics: Even though it has directly contribute to the disease, others can be linked been a decade since researchers first sequenced the to the genes that do (Carmichael, 2010). However, human genome, obvious links between the genes and complications arise when we try to analyze such data, specific diseases have been much slower to appear than due to the fact that the number of possible interaction originally expected by everybody. Because original combinations among genotype markers is humongous approach based on simple correlation analysis was not for a large size genetic association study and we are successful, now many researchers believe that new interested in finding very few disease-related advances in genomics will come from a rich interactions (Zhang and Liu, 2007). Additionally, some statistical understanding of complex interactions of nearby SNPs are highly correlated due to linkage our genetic code (Bansal et al ., 2010; Zhang and Liu, disequilibrium (Zhang et al ., 2011b), which further 2007; Svoboda, 2010). However, it is necessary to complicates statistical analysis aiming at determining perform statistical analysis on a vast amount of data disease related interactions. consisting out of the sequences including millions of Importance of linkage disequilibrium: Linkage genomes in order to completely understand how our Disequilibrium (LD) describes the phenomenon when genetic code interacts with the environment to make the genotypes at nearby markers are highly correlated us the way we are (Svoboda, 2010). (Zhang et al ., 2011a). This correlation arises due to Whole-genome Single Nucleotide Polymorphisms shared ancestry of contemporary chromosomes (The (SNPs) data from individuals in the case-control studies International HapMap Consortium, 2005). LD patterns has potential to help us understand complex interactions have many important applications in biology and among multiple genes (Zhang et al ., 2011a). SNPs can genetics. These patterns can be used for inferring the Corresponding Author: Jing Zhang, Department of Statistics, Faculty of Arts and Sciences, Yale University, New Haven, CT, USA 20 Am. J. of Bioinformatics 1 (1): 20-29, 2012 distribution of cross-over events at short scales which descriptions of RA and T1D genetic landscapes are still are hard to study experimentally, studying gene far from being understood (Coenen and Gregersen, conversion, about which there is only a very limited 2009; WTCCC, 2007). We chose to focus our study on amount of experimental data, understanding the RA and T1D at the same time because they are already evolutionary history of humans and detecting natural known to share common loci and are both autoimmune selection (Wall and Pritchard, 2003). diseases (WTCCC, 2007). Patterns of linkage disequilibrium are unpredictable and very noisy (Wall and Pritchard, 2003). Additionally, Goals of the project: The goal of this project was extent of LD defers from one genomic region to using as a starting point a highly successful approach to another. Population history, fine-scale heterogeneity in classification problems with discrete covariates (Zhang et recombination rates and population genetic models all al ., 2011b) specifically used for determining block-based contribute to noisy appearance of spatial structure of epistasis associations, to develop a statistical model to LD. However, this complex reality is described by a search for disease associated differences in LD-block simple model known as haplotype-block model (Wall structure between control and case groups. We and Pritchard, 2003). According to this model, determined haplotype-block structure for controls and genotype data is divided into discrete blocks with cases independently and used this information to find highly correlated SNPs within each block and regions with genetic variants that could potentially be adjacent blocks are separated by recombination associated with the disease. Our methods were applied to events (Zhang et al ., 2011b; 2004; Ding et al ., the actual large data sets consisting of whole-genome 2005a; 2005b). Even though described model is single nucleotide polymorphisms data from chromosome simple, experimental data confirms its validity (Wall 6 (chr6) for T1D and RA patients and control groups. and Pritchard, 2003; The International HapMap Consortium, 2005). MATERIALS AND METHODS Background on type 1 diabetes and rheumatoid Our problem of using haplotype-block structure for arthritis: Type 1 Diabetes (T1D) affects 0.5% of the whole-genome chr6 SNPs data from patients and world population and 1.4 million US people (Bottini et controls to determine regions of genetic variants that al ., 2004). It is a chronic disease that occurs when not increase susceptibility to the disease can be divided into enough insulin is produces to control the sugar levels in two smaller sub-problems. First, since there is no blood. It can occur at any age but most frequently it is complete experimental data on spatial structure of LD diagnosed in children and young adults (Devendra et for our regions of interest, we determined LD blocks for al ., 2004). Even though the exact cause of the disease is controls and cases using computational statistical unknown, most researchers suspect that there is some methods and then extracted the disease relevant sort of trigger (environmental or viral) that causes an information hidden in the background noise. Each of immune reaction in genetically susceptible group of these steps used different modeling and data analysis people. As of right now, no cure is available and the techniques that are described in detail below. outcome for people with this type of diabetes varies (Devendra et al ., 2004). Previous studies have validated Statistical model for determining block boundaries the hypothesis that common genetic variants play due to linkage disequilibrium: The observations important role in the disease formation (Bottini et al ., consist of genotypes of L SNP markers observed on N 2004; Polychronakos and Li, 2011; Zhang et al ., patients, combined into final data set D. Each marker 2011a). can have one of three values. The goal is to partition Like T1D, Rheumatoid Arthritis (RA) has a L markers into blocks in such a way that the significant genetic contribution to its development but correlations between SNPs in different blocks are the detailed heritability is still not known (Newton et close to zero, yet the number of observed genotype al ., 2004). RA is a chronic disease that is accompanied combinations of SNPs within each block is small. by severe pain that arises from destruction of the Below we describe a method that uses a Bayesian synovial joints (WTCCC, 2007). Even though recent model and a Monte Carlo algorithm to determine advances in the Genome-Wide Association Studies block structure for the given SNPs data set. (GWAS) are starting to show the directions for new therapies and advancement of understanding the General overview: Let B be the block partition complex relationships between different autoimmune variable which has a form of L binary indicators where disorders and their genetic causes, complete value of one (1) corresponds to the start of the next 21 Am. J. of Bioinformatics 1 (1): 20-29, 2012 block. Using multiplication law for conditional particular diplotype. We model the diplotype counts by probability, we can calculate combined probability of the multinomial distribution with its frequency the Data (D) and Block structure (B) to be Eq. 1: parameters following a Dirichlet prior distribution: P∼ b-s Dirichlet(a 1,a 2,…,a 3 ), where Dirichlet density P(D,B) = P(B | D)P(D). (1) function is given by (let K = 3 b-s) Eq. 6: Therefore, we find the posterior probability of the 1 K ai -1 block boundaries given by Eq. 2: f(p,a) =∏ p i (6) B(a) i=1 P(D,B) P(B | D) = (2) P(D) and the normalizing constant B(a) is specified by K ∏ Γ(a ) i=1 i where Γ is the gamma function and a is the Let's consider numerator and denominator of the K Γ(∑ ai ) above equation separately. Using multiplication law i=1 ones more, we can express the numerator as Eq. 3: vector of Dirichlet parameters. Let ni denote the number of counts of a specific diplotype i out of K in the block P(D,B) = P(D | B)P(B) (3) under consideration.
Load more

Recommended publications
  • Investigating the Genetic Basis of Cisplatin-Induced Ototoxicity in Adult South African Patients
    --------------------------------------------------------------------------- Investigating the genetic basis of cisplatin-induced ototoxicity in adult South African patients --------------------------------------------------------------------------- by Timothy Francis Spracklen SPRTIM002 SUBMITTED TO THE UNIVERSITY OF CAPE TOWN In fulfilment of the requirements for the degree MSc(Med) Faculty of Health Sciences UNIVERSITY OF CAPE TOWN University18 December of Cape 2015 Town Supervisor: Prof. Rajkumar S Ramesar Co-supervisor: Ms A Alvera Vorster Division of Human Genetics, Department of Pathology, University of Cape Town 1 The copyright of this thesis vests in the author. No quotation from it or information derived from it is to be published without full acknowledgement of the source. The thesis is to be used for private study or non- commercial research purposes only. Published by the University of Cape Town (UCT) in terms of the non-exclusive license granted to UCT by the author. University of Cape Town Declaration I, Timothy Spracklen, hereby declare that the work on which this dissertation/thesis is based is my original work (except where acknowledgements indicate otherwise) and that neither the whole work nor any part of it has been, is being, or is to be submitted for another degree in this or any other university. I empower the university to reproduce for the purpose of research either the whole or any portion of the contents in any manner whatsoever. Signature: Date: 18 December 2015 ' 2 Contents Abbreviations ………………………………………………………………………………….. 1 List of figures …………………………………………………………………………………... 6 List of tables ………………………………………………………………………………….... 7 Abstract ………………………………………………………………………………………… 10 1. Introduction …………………………………………………………………………………. 11 1.1 Cancer …………………………………………………………………………….. 11 1.2 Adverse drug reactions ………………………………………………………….. 12 1.3 Cisplatin …………………………………………………………………………… 12 1.3.1 Cisplatin’s mechanism of action ……………………………………………… 13 1.3.2 Adverse reactions to cisplatin therapy ……………………………………….
    [Show full text]
  • Molecular Characterization of Acute Myeloid Leukemia by Next Generation Sequencing: Identification of Novel Biomarkers and Targets of Personalized Therapies
    Alma Mater Studiorum – Università di Bologna Dipartimento di Medicina Specialistica, Diagnostica e Sperimentale Dottorato di Ricerca in Oncologia, Ematologia e Patologia XXX Ciclo Settore Scientifico Disciplinare: MED/15 Settore Concorsuale:06/D3 Molecular characterization of acute myeloid leukemia by Next Generation Sequencing: identification of novel biomarkers and targets of personalized therapies Presentata da: Antonella Padella Coordinatore Prof. Pier-Luigi Lollini Supervisore: Prof. Giovanni Martinelli Esame finale anno 2018 Abstract Acute myeloid leukemia (AML) is a hematopoietic neoplasm that affects myeloid progenitor cells and it is one of the malignancies best studied by next generation sequencing (NGS), showing a highly heterogeneous genetic background. The aim of the study was to characterize the molecular landscape of 2 subgroups of AML patients carrying either chromosomal number alterations (i.e. aneuploidy) or rare fusion genes. We performed whole exome sequencing and we integrated the mutational data with transcriptomic and copy number analysis. We identified the cell cycle, the protein degradation, response to reactive oxygen species, energy metabolism and biosynthetic process as the pathways mostly targeted by alterations in aneuploid AML. Moreover, we identified a 3-gene expression signature including RAD50, PLK1 and CDC20 that characterize this subgroup. Taking advantage of RNA sequencing we aimed at the discovery of novel and rare gene fusions. We detected 9 rare chimeric transcripts, of which partner genes were transcription factors (ZEB2, BCL11B and MAFK) or tumor suppressors (SAV1 and PUF60) rarely translocated across cancer types. Moreover, we detected cryptic events hiding the loss of NF1 and WT1, two recurrently altered genes in AML. Finally, we explored the oncogenic potential of the ZEB2-BCL11B fusion, which revealed no transforming ability in vitro.
    [Show full text]
  • Supplementary Table S4. FGA Co-Expressed Gene List in LUAD
    Supplementary Table S4. FGA co-expressed gene list in LUAD tumors Symbol R Locus Description FGG 0.919 4q28 fibrinogen gamma chain FGL1 0.635 8p22 fibrinogen-like 1 SLC7A2 0.536 8p22 solute carrier family 7 (cationic amino acid transporter, y+ system), member 2 DUSP4 0.521 8p12-p11 dual specificity phosphatase 4 HAL 0.51 12q22-q24.1histidine ammonia-lyase PDE4D 0.499 5q12 phosphodiesterase 4D, cAMP-specific FURIN 0.497 15q26.1 furin (paired basic amino acid cleaving enzyme) CPS1 0.49 2q35 carbamoyl-phosphate synthase 1, mitochondrial TESC 0.478 12q24.22 tescalcin INHA 0.465 2q35 inhibin, alpha S100P 0.461 4p16 S100 calcium binding protein P VPS37A 0.447 8p22 vacuolar protein sorting 37 homolog A (S. cerevisiae) SLC16A14 0.447 2q36.3 solute carrier family 16, member 14 PPARGC1A 0.443 4p15.1 peroxisome proliferator-activated receptor gamma, coactivator 1 alpha SIK1 0.435 21q22.3 salt-inducible kinase 1 IRS2 0.434 13q34 insulin receptor substrate 2 RND1 0.433 12q12 Rho family GTPase 1 HGD 0.433 3q13.33 homogentisate 1,2-dioxygenase PTP4A1 0.432 6q12 protein tyrosine phosphatase type IVA, member 1 C8orf4 0.428 8p11.2 chromosome 8 open reading frame 4 DDC 0.427 7p12.2 dopa decarboxylase (aromatic L-amino acid decarboxylase) TACC2 0.427 10q26 transforming, acidic coiled-coil containing protein 2 MUC13 0.422 3q21.2 mucin 13, cell surface associated C5 0.412 9q33-q34 complement component 5 NR4A2 0.412 2q22-q23 nuclear receptor subfamily 4, group A, member 2 EYS 0.411 6q12 eyes shut homolog (Drosophila) GPX2 0.406 14q24.1 glutathione peroxidase
    [Show full text]
  • A Dissertation Entitled the Androgen Receptor
    A Dissertation entitled The Androgen Receptor as a Transcriptional Co-activator: Implications in the Growth and Progression of Prostate Cancer By Mesfin Gonit Submitted to the Graduate Faculty as partial fulfillment of the requirements for the PhD Degree in Biomedical science Dr. Manohar Ratnam, Committee Chair Dr. Lirim Shemshedini, Committee Member Dr. Robert Trumbly, Committee Member Dr. Edwin Sanchez, Committee Member Dr. Beata Lecka -Czernik, Committee Member Dr. Patricia R. Komuniecki, Dean College of Graduate Studies The University of Toledo August 2011 Copyright 2011, Mesfin Gonit This document is copyrighted material. Under copyright law, no parts of this document may be reproduced without the expressed permission of the author. An Abstract of The Androgen Receptor as a Transcriptional Co-activator: Implications in the Growth and Progression of Prostate Cancer By Mesfin Gonit As partial fulfillment of the requirements for the PhD Degree in Biomedical science The University of Toledo August 2011 Prostate cancer depends on the androgen receptor (AR) for growth and survival even in the absence of androgen. In the classical models of gene activation by AR, ligand activated AR signals through binding to the androgen response elements (AREs) in the target gene promoter/enhancer. In the present study the role of AREs in the androgen- independent transcriptional signaling was investigated using LP50 cells, derived from parental LNCaP cells through extended passage in vitro. LP50 cells reflected the signature gene overexpression profile of advanced clinical prostate tumors. The growth of LP50 cells was profoundly dependent on nuclear localized AR but was independent of androgen. Nevertheless, in these cells AR was unable to bind to AREs in the absence of androgen.
    [Show full text]
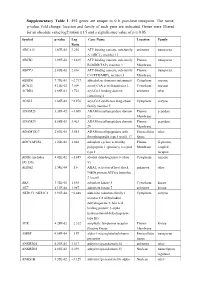
  • Supplementary Table 1
    Supplementary Table 1. 492 genes are unique to 0 h post-heat timepoint. The name, p-value, fold change, location and family of each gene are indicated. Genes were filtered for an absolute value log2 ration 1.5 and a significance value of p ≤ 0.05. Symbol p-value Log Gene Name Location Family Ratio ABCA13 1.87E-02 3.292 ATP-binding cassette, sub-family unknown transporter A (ABC1), member 13 ABCB1 1.93E-02 −1.819 ATP-binding cassette, sub-family Plasma transporter B (MDR/TAP), member 1 Membrane ABCC3 2.83E-02 2.016 ATP-binding cassette, sub-family Plasma transporter C (CFTR/MRP), member 3 Membrane ABHD6 7.79E-03 −2.717 abhydrolase domain containing 6 Cytoplasm enzyme ACAT1 4.10E-02 3.009 acetyl-CoA acetyltransferase 1 Cytoplasm enzyme ACBD4 2.66E-03 1.722 acyl-CoA binding domain unknown other containing 4 ACSL5 1.86E-02 −2.876 acyl-CoA synthetase long-chain Cytoplasm enzyme family member 5 ADAM23 3.33E-02 −3.008 ADAM metallopeptidase domain Plasma peptidase 23 Membrane ADAM29 5.58E-03 3.463 ADAM metallopeptidase domain Plasma peptidase 29 Membrane ADAMTS17 2.67E-04 3.051 ADAM metallopeptidase with Extracellular other thrombospondin type 1 motif, 17 Space ADCYAP1R1 1.20E-02 1.848 adenylate cyclase activating Plasma G-protein polypeptide 1 (pituitary) receptor Membrane coupled type I receptor ADH6 (includes 4.02E-02 −1.845 alcohol dehydrogenase 6 (class Cytoplasm enzyme EG:130) V) AHSA2 1.54E-04 −1.6 AHA1, activator of heat shock unknown other 90kDa protein ATPase homolog 2 (yeast) AK5 3.32E-02 1.658 adenylate kinase 5 Cytoplasm kinase AK7
    [Show full text]
  • Modeling Genomic Diversity and Tumor Dependency in Malignant Melanoma
    Research Article Modeling Genomic Diversity and Tumor Dependency in Malignant Melanoma William M. Lin,1,3,5 Alissa C. Baker,1,3 Rameen Beroukhim,1,3,5 Wendy Winckler,1,3,5 Whei Feng,1,3,5 Jennifer M. Marmion,7 Elisabeth Laine,8 Heidi Greulich,1,3,5 Hsiuyi Tseng,1,3 Casey Gates,5 F. Stephen Hodi,1 Glenn Dranoff,1 William R. Sellers,1,6 Roman K. Thomas,9,10 Matthew Meyerson,1,3,4,5 Todd R. Golub,2,3,5 Reinhard Dummer,8 Meenhard Herlyn,7 Gad Getz,3,5 and Levi A. Garraway1,3,5 Departments of 1Medical Oncology and 2Pediatric Oncology and 3Center for Cancer Genome Discovery, Dana-Farber Cancer Institute, Harvard Medical School; 4Department of Pathology, Harvard Medical School, Boston, Massachusetts; 5The Broad Institute of M.I.T. and Harvard; 6Novartis Institutes for Biomedical Research, Cambridge, Massachusetts; 7Cancer Biology Division, Wistar Institute, Philadelphia, Pennsylvania; 8Department of Dermatology, University of Zurich Hospital, Zu¨rich, Switzerland; 9Max Planck Institute for Neurological Research with Klaus Joachim Zulch Laboratories of the Max Planck Society and the Medical Faculty of the University of Cologne; and 10Center for Integrated Oncology and Department I for Internal Medicine, University of Cologne, Cologne, Germany Abstract tumorigenesis have been derived from functional studies involving The classification of human tumors based on molecular cultured human cancer cells (e.g., established cell lines, short-term cultures, etc.). Despite their limitations, cancer cell line collections criteria offers tremendous clinical potential; however, dis- cerning critical and ‘‘druggable’’ effectors on a large scale will whose genetic alterations reflect their primary tumor counterparts also require robust experimental models reflective of tumor should provide malleable proxies that facilitate mechanistic genomic diversity.
    [Show full text]
  • Identification of a Clinically Relevant Androgen-Dependent Gene Signature in Prostate Cancer
    Published OnlineFirst February 15, 2011; DOI: 10.1158/0008-5472.CAN-10-2512 Cancer Tumor and Stem Cell Biology Research Identification of a Clinically Relevant Androgen-Dependent Gene Signature in Prostate Cancer Hannelore V. Heemers1, Lucy J. Schmidt3, Zhifu Sun4, Kevin M. Regan3, S. Keith Anderson5, Kelly Duncan1, Dan Wang2, Song Liu2, Karla V. Ballman5, and Donald J. Tindall3 Abstract The androgen receptor (AR) is the principal target for treatment of non–organ-confined prostate cancer (PCa). Androgen deprivation therapies (ADT) directed against the AR ligand–binding domain do not fully inhibit androgen-dependent signaling critical for PCa progression. Thus, information that could direct the development of more effective ADTs is desired. Systems and bioinformatics approaches suggest that considerable variation exists in the mechanisms by which AR regulates expression of effector genes, pointing to a role for secondary transcription factors. A combination of microarray and in silico analyses led us to identify a 158-gene signature that relies on AR along with the transcription factor SRF (serum response factor), representing less than 6% of androgen-dependent genes. This AR-SRF signature is sufficient to distinguish microdissected benign and malignant prostate samples, and it correlates with the presence of aggressive disease and poor outcome. The AR- SRF signature described here associates more strongly with biochemical failure than other AR target gene signatures of similar size. Furthermore, it is enriched in malignant versus benign prostate tissues, compared with other signatures. To our knowledge, this profile represents the first demonstration of a distinct mechanism of androgen action with clinical relevance in PCa, offering a possible rationale to develop novel and more effective forms of ADT.
    [Show full text]
  • Chapter 2: a Technique for Generating Unbiased Whole Genome
    UC San Diego UC San Diego Electronic Theses and Dissertations Title Massively Parallel Polymerase Cloning and Genome Sequencing of Single Cells Using the Microwell Displacement Amplification System (MIDAS) / Permalink https://escholarship.org/uc/item/8kn4n1wd Author Gole, Jeffrey Publication Date 2013 Peer reviewed|Thesis/dissertation eScholarship.org Powered by the California Digital Library University of California UNIVERSITY OF CALIFORNIA, SAN DIEGO Massively Parallel Polymerase Cloning and Genome Sequencing of Single Cells Using the Microwell Displacement Amplification System (MIDAS) A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Bioengineering by Jeffrey Gole Committee in charge: Professor Kun Zhang, Chair Professor Vineet Bafna Professor Michael Heller Professor Xiaohua Huang Professor Yu-Hwa Lo 2013 Copyright Jeffrey Gole, 2013 All rights reserved The Dissertation of Jeffrey Gole is approved, and it is acceptable in quality and form for publication on microfilm and electronically: Chair University of California, San Diego 2013 iii DEDICATION For my parents iv TABLE OF CONTENTS SIGNATURE PAGE………………………………………………………………....iii DEDICATION ................................................................................................... iv TABLE OF CONTENTS ....................................................................................v LIST OF FIGURES.......................................................................................... vii LIST OF TABLES............................................................................................viii
    [Show full text]
  • Exploring BCR-ABL-Independent Mechanisms of TKI-Resistance in Chronic Myeloid Leukaemia
    Mitchell, Rebecca (2017) Exploring BCR-ABL-independent mechanisms of TKI-resistance in chronic myeloid leukaemia. PhD thesis. https://theses.gla.ac.uk/7977/ Copyright and moral rights for this work are retained by the author A copy can be downloaded for personal non-commercial research or study, without prior permission or charge This work cannot be reproduced or quoted extensively from without first obtaining permission in writing from the author The content must not be changed in any way or sold commercially in any format or medium without the formal permission of the author When referring to this work, full bibliographic details including the author, title, awarding institution and date of the thesis must be given Enlighten: Theses https://theses.gla.ac.uk/ [email protected] Exploring BCR-ABL-independent mechanisms of TKI-Resistance in Chronic Myeloid Leukaemia By Rebecca Mitchell BSc (Hons), MRes Submitted in the fulfilment of the requirements for the degree of Doctor of Philosophy September 2016 Section of Experimental Haematology Institute of Cancer Sciences College of Medical, Veterinary and Life Science University of Glasgow 2 Abstract As the prevalence of Chronic Myeloid Leukaemia (CML) grows, due to the therapeutic success of tyrosine kinase inhibitors (TKI), we are witnessing increased incidences of drug resistance. Some of these patients have failed all currently licensed TKIs and have no mutational changes in the kinase domain that may explain the cause of TKI resistance. This poses a major clinical challenge as there are currently no other drug treatment options available for these patients. Therefore, our aim was to identify and target alternative survival pathways against BCR-ABL in order to eradicate TKI-resistant cells.
    [Show full text]
  • Hypoxia As an Evolutionary Force
    “The genetic architecture of adaptations to high altitude in Ethiopia” Gorka Alkorta-Aranburu1, Cynthia M. Beall2*, David B. Witonsky1, Amha Gebremedhin3, Jonathan K. Pritchard1,4, Anna Di Rienzo1* 1 Department of Human Genetics, University of Chicago, Chicago, Illinois, United States of America, 2 Department of Anthropology, Case Western Research University, Cleveland, Ohio, United States of America, 3 Department of Internal Medicine, Faculty of Medicine, Addis Ababa University, Addis Ababa, Ethiopia, 4 Howard Hughes Medical Institute * E-mail: [email protected] and [email protected] Corresponding authors: Anna Di Rienzo Department of Human Genetics University of Chicago 920 E. 58th Street Chicago, IL 60637, USA. Cynthia M. Beall Anthropology Department Case Western Reserve University 238 Mather Memorial Building 11220 Bellflower Road Cleveland, OH 44106, USA. 1 ABSTRACT Although hypoxia is a major stress on physiological processes, several human populations have survived for millennia at high altitudes, suggesting that they have adapted to hypoxic conditions. This hypothesis was recently corroborated by studies of Tibetan highlanders, which showed that polymorphisms in candidate genes show signatures of natural selection as well as well-replicated association signals for variation in hemoglobin levels. We extended genomic analysis to two Ethiopian ethnic groups: Amhara and Oromo. For each ethnic group, we sampled low and high altitude residents, thus allowing genetic and phenotypic comparisons across altitudes and across ethnic groups. Genome- wide SNP genotype data were collected in these samples by using Illumina arrays. We find that variants associated with hemoglobin variation among Tibetans or other variants at the same loci do not influence the trait in Ethiopians.
    [Show full text]
  • WO 2012/058097 Al
    (12) INTERNATIONAL APPLICATION PUBLISHED UNDER THE PATENT COOPERATION TREATY (PCT) (19) World Intellectual Property Organization International Bureau (10) International Publication Number (43) International Publication Date 3 May 2012 (03.05.2012) WO 2012/058097 Al (51) International Patent Classification: (81) Designated States (unless otherwise indicated, for every CI2N 5/00 (2006.01) kind of national protection available): AE, AG, AL, AM, AO, AT, AU, AZ, BA, BB, BG, BH, BR, BW, BY, BZ, (21) International Application Number: CA, CH, CL, CN, CO, CR, CU, CZ, DE, DK, DM, DO, PCT/US20 11/057140 DZ, EC, EE, EG, ES, FI, GB, GD, GE, GH, GM, GT, (22) International Filing Date: HN, HR, HU, ID, IL, IN, IS, JP, KE, KG, KM, KN, KP, 20 October 201 1 (20.10.201 1) KR, KZ, LA, LC, LK, LR, LS, LT, LU, LY, MA, MD, ME, MG, MK, MN, MW, MX, MY, MZ, NA, NG, NI, (25) Filing Language: English NO, NZ, OM, PE, PG, PH, PL, PT, QA, RO, RS, RU, (26) Publication Language: English RW, SC, SD, SE, SG, SK, SL, SM, ST, SV, SY, TH, TJ, TM, TN, TR, TT, TZ, UA, UG, US, UZ, VC, VN, ZA, (30) Priority Data: ZM, ZW. 61/455,808 26 October 2010 (26.10.2010) US 61/406,954 26 October 2010 (26.10.2010) US (84) Designated States (unless otherwise indicated, for every kind of regional protection available): ARIPO (BW, GH, (71) Applicant (for all designated States except US): BUCK GM, KE, LR, LS, MW, MZ, NA, RW, SD, SL, SZ, TZ, INSTITUTE FOR AGE RESEARCH [US/US]; 8001 UG, ZM, ZW), Eurasian (AM, AZ, BY, KG, KZ, MD, Redwood Boulevard, Novate, California 94945 (US).
    [Show full text]
  • Ed with LMP1 Gene in Nasopharyngeal Carcinoma
    bioRxiv preprint doi: https://doi.org/10.1101/615237; this version posted April 29, 2019. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC-ND 4.0 International license. 1 Integrated analysis of the miRNA-mRNA network associat- 2 ed with LMP1 gene in nasopharyngeal carcinoma 3 Short title: A co-analysis of EBV-associated genes in NPC 4 5 Autho list:Yang Yanga, Wen Liua, Yan Zhanga,b, Shuo Wua, Bing Luoa* 6 7 Affilation: 8 a: Department of Pathogenic Biology, Qingdao University Medical College, 38 Dengzhou Road, 9 Qingdao, 266071, China 10 b: Department of Clinical Laboratory, Central Hospital of Zibo, 54 Gongqingtuan Road, ZiBo, 11 255036, China 12 13 *Corresponding author: Bing Luo 14 Affilation: Department of Pathogenic Biology, Qingdao University Medical College, 38 Dengzhou 15 Road, Qingdao, 266071, China. Tel: 86-532-8299108. 16 17 Abstract: Epstein-Barr virus oncogenic latent membrane protein 1 (LMP1) has been known to 18 play important roles in nasopharyngeal carcinoma (NPC). LMP1 gene also induced a variety of 19 microRNAs (miRNAs) which bear pivotal roles in regulation of mRNAs expression. However, 20 little was known about the global change of mRNAs and miRNAs induced by LMP1 gene in NPC. 21 In our study, one NPC tissue microarray profile and two LMP1-associated microarray expression 22 profiles data were downloaded from the Gene Expression Omnibus database. A protein-protein 23 interaction network was constructed by using bioinformatics platform Gene-Cloud of Biotech- 24 nology Information (GCBI).
    [Show full text]