Analysis on Some Basic Ion Channel Modeling Problems
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

A Computational Model of Large Conductance Voltage and Calcium
Journal of Computational Neuroscience (2019) 46:233–256 https://doi.org/10.1007/s10827-019-00713-9 A computational model of large conductance voltage and calcium activated potassium channels: implications for calcium dynamics and electrophysiology in detrusor smooth muscle cells Suranjana Gupta1 · Rohit Manchanda1 Received: 11 September 2018 / Revised: 14 February 2019 / Accepted: 19 February 2019 / Published online: 25 April 2019 © Springer Science+Business Media, LLC, part of Springer Nature 2019 Abstract The large conductance voltage and calcium activated potassium (BK) channels play a crucial role in regulating the excitability of detrusor smooth muscle, which lines the wall of the urinary bladder. These channels have been widely characterized in terms of their molecular structure, pharmacology and electrophysiology. They control the repolarising and hyperpolarising phases of the action potential, thereby regulating the firing frequency and contraction profiles of the smooth muscle. Several groups have reported varied profiles of BK currents and I-V curves under similar experimental conditions. However, no single computational model has been able to reconcile these apparent discrepancies. In view of the channels’ physiological importance, it is imperative to understand their mechanistic underpinnings so that a realistic model can be created. This paper presents a computational model of the BK channel, based on the Hodgkin-Huxley formalism, constructed by utilising three activation processes — membrane potential, calcium inflow from voltage-gated calcium channels on the membrane and calcium released from the ryanodine receptors present on the sarcoplasmic reticulum. In our model, we attribute the discrepant profiles to the underlying cytosolic calcium received by the channel during its activation. The model enables us to make heuristic predictions regarding the nature of the sub-membrane calcium dynamics underlying the BK channel’s activation. -

Entropy-Based Regulation of Cluster Ion Channel Density
www.nature.com/scientificreports OPEN Molecular and cellular correlates in Kv channel clustering: entropy‑based regulation of cluster ion channel density Limor Lewin1, Esraa Nsasra1, Ella Golbary1, Uzi Hadad2, Irit Orr1 & Ofer Yifrach1* Scafold protein-mediated ion channel clustering at unique membrane sites is important for electrical signaling. Yet, the mechanism(s) by which scafold protein-ion channel interactions lead to channel clustering or how cluster ion channel density is regulated is mostly not known. The voltage‑activated potassium channel (Kv) represents an excellent model to address these questions as the mechanism underlying its interaction with the post-synaptic density 95 (PSD-95) scafold protein is known to be controlled by the length of the extended ‘ball and chain’ sequence comprising the C-terminal channel region. Here, using sub-difraction high-resolution imaging microscopy, we show that Kv channel ‘chain’ length regulates Kv channel density with a ‘bell’-shaped dependence, refecting a balance between thermodynamic considerations controlling ‘chain’ recruitment by PSD-95 and steric hindrance due to the spatial proximity of multiple channel molecules. Our results thus reveal an entropy‑based mode of channel cluster density regulation that mirrors the entropy‑based regulation of the Kv channel-PSD-95 interaction. The implications of these fndings for electrical signaling are discussed. Action potential generation, propagation and the evoked synaptic potential all rely on precisely timed events associated with activation and inactivation gating transitions of voltage-dependent Na + and K + channels, clus- tered in multiple copies at unique membrane sites, such as the initial segment of an axon, nodes of Ranvier, pre-synaptic terminals or at the post-synaptic density (PSD)1–3. -

Modeling of Voltage-Gated Ion Channels
Modeling of voltage-gated ion channels Modeling of voltage-gated ion channels Pär Bjelkmar c Pär Bjelkmar, Stockholm 2011, pages 1-65 Cover picture: Produced by Pär Bjelkmar and Jyrki Hokkanen at CSC - IT Center for Science, Finland. Cover of PLoS Computational Biology February 2009 issue. ISBN 978-91-7447-336-0 Printed in Sweden by US-AB, Stockholm 2011 Distributor: Department of Biochemistry and Biophysics, Stockholm University Abstract The recent determination of several crystal structures of voltage-gated ion channels has catalyzed computational efforts of studying these re- markable molecular machines that are able to conduct ions across bi- ological membranes at extremely high rates without compromising the ion selectivity. Starting from the open crystal structures, we have studied the gating mechanism of these channels by molecular modeling techniques. Firstly, by applying a membrane potential, initial stages of the closing of the channel were captured, manifested in a secondary-structure change in the voltage-sensor. In a follow-up study, we found that the energetic cost of translocating this 310-helix was significantly lower than in the origi- nal conformation. Thirdly, collaborators of ours identified new molecular constraints for different states along the gating pathway. We used those to build new protein models that were evaluated by simulations. All these results point to a gating mechanism where the S4 helix undergoes a secondary structure transformation during gating. These simulations also provide information about how the protein in- teracts with the surrounding membrane. In particular, we found that lipid molecules close to the protein diffuse together with it, forming a large dynamic lipid-protein cluster. -

Stem Cells and Ion Channels
Stem Cells International Stem Cells and Ion Channels Guest Editors: Stefan Liebau, Alexander Kleger, Michael Levin, and Shan Ping Yu Stem Cells and Ion Channels Stem Cells International Stem Cells and Ion Channels Guest Editors: Stefan Liebau, Alexander Kleger, Michael Levin, and Shan Ping Yu Copyright © 2013 Hindawi Publishing Corporation. All rights reserved. This is a special issue published in “Stem Cells International.” All articles are open access articles distributed under the Creative Com- mons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Editorial Board Nadire N. Ali, UK Joseph Itskovitz-Eldor, Israel Pranela Rameshwar, USA Anthony Atala, USA Pavla Jendelova, Czech Republic Hannele T. Ruohola-Baker, USA Nissim Benvenisty, Israel Arne Jensen, Germany D. S. Sakaguchi, USA Kenneth Boheler, USA Sue Kimber, UK Paul R. Sanberg, USA Dominique Bonnet, UK Mark D. Kirk, USA Paul T. Sharpe, UK B. Bunnell, USA Gary E. Lyons, USA Ashok Shetty, USA Kevin D. Bunting, USA Athanasios Mantalaris, UK Igor Slukvin, USA Richard K. Burt, USA Pilar Martin-Duque, Spain Ann Steele, USA Gerald A. Colvin, USA EvaMezey,USA Alexander Storch, Germany Stephen Dalton, USA Karim Nayernia, UK Marc Turner, UK Leonard M. Eisenberg, USA K. Sue O’Shea, USA Su-Chun Zhang, USA Marina Emborg, USA J. Parent, USA Weian Zhao, USA Josef Fulka, Czech Republic Bruno Peault, USA Joel C. Glover, Norway Stefan Przyborski, UK Contents Stem Cells and Ion Channels, Stefan Liebau, -

Download File
STRUCTURAL AND FUNCTIONAL STUDIES OF TRPML1 AND TRPP2 Nicole Marie Benvin Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the Graduate School of Arts and Sciences COLUMBIA UNIVERSITY 2017 © 2017 Nicole Marie Benvin All Rights Reserved ABSTRACT Structural and Functional Studies of TRPML1 and TRPP2 Nicole Marie Benvin In recent years, the determination of several high-resolution structures of transient receptor potential (TRP) channels has led to significant progress within this field. The primary focus of this dissertation is to elucidate the structural characterization of TRPML1 and TRPP2. Mutations in TRPML1 cause mucolipidosis type IV (MLIV), a rare neurodegenerative lysosomal storage disorder. We determined the first high-resolution crystal structures of the human TRPML1 I-II linker domain using X-ray crystallography at pH 4.5, pH 6.0, and pH 7.5. These structures revealed a tetramer with a highly electronegative central pore which plays a role in the dual Ca2+/pH regulation of TRPML1. Notably, these physiologically relevant structures of the I-II linker domain harbor three MLIV-causing mutations. Our findings suggest that these pathogenic mutations destabilize not only the tetrameric structure of the I-II linker, but also the overall architecture of full-length TRPML1. In addition, TRPML1 proteins containing MLIV- causing mutations mislocalized in the cell when imaged by confocal fluorescence microscopy. Mutations in TRPP2 cause autosomal dominant polycystic kidney disease (ADPKD). Since novel technological advances in single-particle cryo-electron microscopy have now enabled the determination of high-resolution membrane protein structures, we set out to solve the structure of TRPP2 using this technique. -

The Role of TRP Proteins in Mast Cells
View metadata, citation and similar papers at core.ac.uk brought to you by CORE REVIEW ARTICLE published: 12 Juneprovided 2012 by Frontiers - Publisher Connector doi: 10.3389/fimmu.2012.00150 The role ofTRP proteins in mast cells Marc Freichel*, Julia Almering and VolodymyrTsvilovskyy Pharmakologisches Institut, Universität Heidelberg, Heidelberg, Germany Edited by: Transient receptor potential (TRP) proteins form cation channels that are regulated through Ulrich Blank, Université Paris-Diderot strikingly diverse mechanisms including multiple cell surface receptors, changes in tem- Paris 7, France 2+ 2+ perature, in pH and osmolarity, in cytosolic free Ca concentration ([Ca ]i), and by Reviewed by: Marc Benhamou, Institut National de phosphoinositides which makes them polymodal sensors for fine tuning of many cellu- la Santé et de la Recherche Médicale, lar and systemic processes in the body. The 28 TRP proteins identified in mammals are France classified into six subfamilies: TRPC, TRPV, TRPM, TRPA, TRPML, and TRPP.When acti- Pierre Launay, Institut National de la vated, they contribute to cell depolarization and Ca2+ entry. In mast cells, the increase of Santé et de la Recherche Médicale, 2+ 2+ France [Ca ]i is fundamental for their biological activity, and several entry pathways for Ca and 2+ 2+ *Correspondence: other cations were described including Ca release activated Ca (CRAC) channels. Like 2+ Marc Freichel, Pharmakologisches in other non-excitable cells, TRP channels could directly contribute to Ca influx via the Institut, Universität Heidelberg, Im plasma membrane as constituents of Ca2+ conducting channel complexes or indirectly by Neuenheimer Feld 366, 69120 shifting the membrane potential and regulation of the driving force for Ca2+ entry through Heidelberg, Germany. -
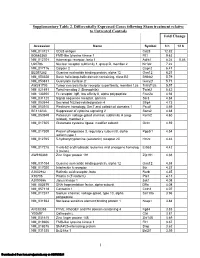
Supplementary Table 2
Supplementary Table 2. Differentially Expressed Genes following Sham treatment relative to Untreated Controls Fold Change Accession Name Symbol 3 h 12 h NM_013121 CD28 antigen Cd28 12.82 BG665360 FMS-like tyrosine kinase 1 Flt1 9.63 NM_012701 Adrenergic receptor, beta 1 Adrb1 8.24 0.46 U20796 Nuclear receptor subfamily 1, group D, member 2 Nr1d2 7.22 NM_017116 Calpain 2 Capn2 6.41 BE097282 Guanine nucleotide binding protein, alpha 12 Gna12 6.21 NM_053328 Basic helix-loop-helix domain containing, class B2 Bhlhb2 5.79 NM_053831 Guanylate cyclase 2f Gucy2f 5.71 AW251703 Tumor necrosis factor receptor superfamily, member 12a Tnfrsf12a 5.57 NM_021691 Twist homolog 2 (Drosophila) Twist2 5.42 NM_133550 Fc receptor, IgE, low affinity II, alpha polypeptide Fcer2a 4.93 NM_031120 Signal sequence receptor, gamma Ssr3 4.84 NM_053544 Secreted frizzled-related protein 4 Sfrp4 4.73 NM_053910 Pleckstrin homology, Sec7 and coiled/coil domains 1 Pscd1 4.69 BE113233 Suppressor of cytokine signaling 2 Socs2 4.68 NM_053949 Potassium voltage-gated channel, subfamily H (eag- Kcnh2 4.60 related), member 2 NM_017305 Glutamate cysteine ligase, modifier subunit Gclm 4.59 NM_017309 Protein phospatase 3, regulatory subunit B, alpha Ppp3r1 4.54 isoform,type 1 NM_012765 5-hydroxytryptamine (serotonin) receptor 2C Htr2c 4.46 NM_017218 V-erb-b2 erythroblastic leukemia viral oncogene homolog Erbb3 4.42 3 (avian) AW918369 Zinc finger protein 191 Zfp191 4.38 NM_031034 Guanine nucleotide binding protein, alpha 12 Gna12 4.38 NM_017020 Interleukin 6 receptor Il6r 4.37 AJ002942 -

Study of Selectivity and Permeation in Voltage-Gated Ion Channels
Study of Selectivity and Permeation in Voltage-Gated Ion Channels By Janhavi Giri, Ph.D. Visiting Research Faculty Division of Molecular Biophysics and Physiology Rush University Medical Center Chicago, IL, USA Email: [email protected] i TABLE OF CONTENTS Page TABLE OF CONTENTS ..................................................................................................... i LIST OF TABLES ............................................................................................................. iii LIST OF FIGURES ........................................................................................................... iv SUMMARY ............................................................................................................... xvi CHAPTER 1. INTRODUCTION ....................................................................................... 1 1.1. Background ................................................................................................... 1 1.2. Overview .................................................................................................... 10 CHAPTER 2. SELF-ORGANIZED MODELS OF SELECTIVITY IN CALCIUM CHANNELS ........................................................................................... 13 2.1. Introduction ................................................................................................ 13 2.2. Methods ...................................................................................................... 19 2.2.1. Model of Channel and Electrolyte ........................................................19 -

Novel Voltage Dependent Ion Channel Fusions and Method of Use Thereof
(19) TZZ¥ZZ _T (11) EP 3 056 902 A1 (12) EUROPEAN PATENT APPLICATION (43) Date of publication: (51) Int Cl.: 17.08.2016 Bulletin 2016/33 G01N 33/542 (2006.01) C07K 14/705 (2006.01) (21) Application number: 15155202.3 (22) Date of filing: 16.02.2015 (84) Designated Contracting States: (72) Inventors: AL AT BE BG CH CY CZ DE DK EE ES FI FR GB • Ruigrok, Hermanus GR HR HU IE IS IT LI LT LU LV MC MK MT NL NO 33200 Bordeaux (FR) PL PT RO RS SE SI SK SM TR • Percherancier, Yann Designated Extension States: 33140 Villenave d’Ornon (FR) BA ME •Veyret,Bernard 33600 PESSAC (FR) (71) Applicants: • UNIVERSITE DE BORDEAUX (74) Representative: Lecca, Patricia S. 33000 Bordeaux (FR) Cabinet Lecca • CENTRE NATIONAL DE LA RECHERCHE 21, rue de Fécamp SCIENTIFIQUE 75012 Paris (FR) 75794 Paris Cedex 16 (FR) • Institut Polytechnique de Bordeaux 33402 Talence Cedex (FR) (54) Novel voltage dependent ion channel fusions and method of use thereof (57) The present invention relates to novel volt- izing candidate molecules or physical parameters for age-dependent ion channel fusion subunits, and to a their ability to activate or inhibit voltage-dependent ion functional bioluminescence resonance energy transfer channels. (BRET) assay for screening in real time and character- EP 3 056 902 A1 Printed by Jouve, 75001 PARIS (FR) EP 3 056 902 A1 Description FIELD OF THE INVENTION 5 [0001] The present invention relates to novel voltage-dependent ion channel fusion subunits, and to a functional bioluminescence resonance energy transfer (BRET) assay for screening in real time and characterizing candidate mol- ecules or physical parameters for their ability to activate or inhibit voltage-dependent ion channels. -

Transient Receptor Potential Channels As Drug Targets: from the Science of Basic Research to the Art of Medicine
1521-0081/66/3/676–814$25.00 http://dx.doi.org/10.1124/pr.113.008268 PHARMACOLOGICAL REVIEWS Pharmacol Rev 66:676–814, July 2014 Copyright © 2014 by The American Society for Pharmacology and Experimental Therapeutics ASSOCIATE EDITOR: DAVID R. SIBLEY Transient Receptor Potential Channels as Drug Targets: From the Science of Basic Research to the Art of Medicine Bernd Nilius and Arpad Szallasi KU Leuven, Department of Cellular and Molecular Medicine, Laboratory of Ion Channel Research, Campus Gasthuisberg, Leuven, Belgium (B.N.); and Department of Pathology, Monmouth Medical Center, Long Branch, New Jersey (A.S.) Abstract. ....................................................................................679 I. Transient Receptor Potential Channels: A Brief Introduction . ...............................679 A. Canonical Transient Receptor Potential Subfamily . .....................................682 B. Vanilloid Transient Receptor Potential Subfamily . .....................................686 C. Melastatin Transient Receptor Potential Subfamily . .....................................696 Downloaded from D. Ankyrin Transient Receptor Potential Subfamily .........................................700 E. Mucolipin Transient Receptor Potential Subfamily . .....................................702 F. Polycystic Transient Receptor Potential Subfamily . .....................................703 II. Transient Receptor Potential Channels: Hereditary Diseases (Transient Receptor Potential Channelopathies). ......................................................704 -

The Role of the Secondary Messenger NAADP in Physiological and Pathological Calcium Signalling in Pancreatic Acinar Cells
The role of the secondary messenger NAADP in physiological and pathological calcium signalling in pancreatic acinar cells Thesis submitted in accordance with the requirements of Cardiff University for the degree of Doctor of Philosophy Martyn Richard Charlesworth April, 2017 To my Mother For the inspiration she provided and the endless support, encouragement and faith she has given me throughout. 2 Abstract Acute Pancreatitis (AP) is inflammatory disease characterised by the pathological activation of the digestive enzymes and extensive necrosis of the pancreases and surrounding tissue, which currently has no effective treatment. Pathological agents like the bile acid taurolithocholic acid-3-sulfate (TLC-S) have been shown to induce necrosis of pancreatic acinar cells by causing intracellular calcium (Ca2+) to reach cytotoxic concentrations. TLC-S acts on elements of the secondary Ca2+ messenger pathways normally used in physiological signalling to achieve these Ca2+ increases. Nicotinic acid adenine dinucleotide phosphate (NAADP) is the most novel of these secondary Ca2+ messengers to be identified and several recent advancements have been made regarding its activity. This study has used these advancements to better characterise NAADP-induced Ca2+ release in PAC, and its role in both physiological and pathological Ca2+ signalling. NAADP-induced Ca2+ release was found to involve the activity of both Two-pore channel (TPC) and Ryanodine receptor (RyR) Ca2+ channels; with a varying involvement of the 2 TPC and 3 RyR isoforms. The NAADP antagonist Ned-19 completely inhibited Ca2+ responses to a physiological concentration of the secretagogue cholecystokinin (CCK) and had a protective effect against a pathological concentration of CCK. The size of the Ca2+ response to TLC-S was significantly inhibited in the presence of Ned-19, and the antagonist significantly reduced the amount of necrosis induced. -

TRP Channels of Intracellular Membranes
JOURNAL OF NEUROCHEMISTRY | 2010 | 113 | 313–328 doi: 10.1111/j.1471-4159.2010.06626.x The Department of Molecular, Cellular, and Developmental Biology, University of Michigan, Ann Arbor, Michigan, USA Abstract potential (TRP) proteins are a superfamily (28 members in Ion channels are classically understood to regulate the flux of mammal) of Ca2+-permeable channels with diverse tissue ions across the plasma membrane in response to a variety of distribution, subcellular localization, and physiological func- environmental and intracellular cues. Ion channels serve a tions. Almost all mammalian TRP channels studied thus far, number of functions in intracellular membranes as well. These like their ancestor yeast TRP channel (TRPY1) that localizes channels may be temporarily localized to intracellular mem- to the vacuole compartment, are also (in addition to their branes as a function of their biosynthetic or secretory path- plasma membrane localization) found to be localized to ways, i.e., en route to their destination location. Intracellular intracellular membranes. Accumulated evidence suggests membrane ion channels may also be located in the endocytic that intracellularly-localized TRP channels actively participate pathways, either being recycled back to the plasma mem- in regulating membrane traffic, signal transduction, and brane or targeted to the lysosome for degradation. Several vesicular ion homeostasis. This review aims to provide a channels do participate in intracellular signal transduction; the summary of these recent works. The discussion will also be most well known example is the inositol 1,4,5-trisphosphate extended to the basic membrane and electrical properties of receptor (IP3R) in the endoplasmic reticulum. Some organellar the TRP-residing compartments.