Hjones Future Growth in Space
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

New Idea for Dyson Sphere Proposed 30 March 2015, by Bob Yirka
New idea for Dyson sphere proposed 30 March 2015, by Bob Yirka that the massive amount of material needed to build such a sphere would be untenable, thus, a more likely scenario would be a civilization building a ring of energy capturing satellites which could be continually expanded. But the notion of the sphere persists and so some scientists continue to look for one, believing that if such a sphere were built, the process of capturing the energy from the interior sun would cause an unmistakable infrared signature, allowing us to notice its presence. But thus far, no such signatures have been found. That might be because we are alone in the universe, or, as Semiz and O?ur argue, it might be because we are looking at the wrong types of stars. They suggest that it would seem to make more sense for an advanced civilization to build their sphere around a white A Dyson Sphere with 1 AU radius in Sol system. Credit: dwarf, rather than a star that is in its main arXiv:1503.04376 [physics.pop-ph] sequence, such as our sun—not only would the sphere be smaller (they have even calculated an estimate for a sphere just one meter thick—1023 (Phys.org)—A pair of Turkish space scientists with kilograms of matter) but the gravity at its surface Bogazici University has proposed that researchers would be similar to their home planet (assuming it looking for the existence of Dyson spheres might were similar to ours). be looking at the wrong objects. ?brahim Semiz and Salim O?ur have written a paper and uploaded Unfortunately, if Semiz and O?ur are right, we may it to the preprint server arXiv, in which they suggest not be able to prove it for many years, as the that if an advanced civilization were to build a luminosity of a white dwarf is much less than other Dyson sphere, it would make the most sense to stars, making it extremely difficult to determine if build it around a white dwarf. -
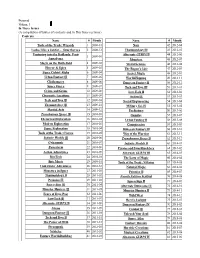
Pyramid Volume 3 in These Issues (A Compilation of Tables of Contents and in This Issue Sections) Contents Name # Month Tools Of
Pyramid Volume 3 In These Issues (A compilation of tables of contents and In This Issue sections) Contents Name # Month Name # Month Tools of the Trade: Wizards 1 2008-11 Noir 42 2012-04 Looks Like a Job for… Superheroes 2 2008-12 Thaumatology III 43 2012-05 Venturing into the Badlands: Post- Alternate GURPS II 44 2012-06 3 2009-01 Apocalypse Monsters 45 2012-07 Magic on the Battlefield 4 2009-02 Weird Science 46 2012-08 Horror & Spies 5 2009-03 The Rogue's Life 47 2012-09 Space Colony Alpha 6 2009-04 Secret Magic 48 2012-10 Urban Fantasy [I] 7 2009-05 World-Hopping 49 2012-11 Cliffhangers 8 2009-06 Dungeon Fantasy II 50 2012-12 Space Opera 9 2009-07 Tech and Toys III 51 2013-01 Crime and Grime 10 2009-08 Low-Tech II 52 2013-02 Cinematic Locations 11 2009-09 Action [I] 53 2013-03 Tech and Toys [I] 12 2009-10 Social Engineering 54 2013-04 Thaumatology [I] 13 2009-11 Military Sci-Fi 55 2013-05 Martial Arts 14 2009-12 Prehistory 56 2013-06 Transhuman Space [I] 15 2010-01 Gunplay 57 2013-07 Historical Exploration 16 2010-02 Urban Fantasy II 58 2013-08 Modern Exploration 17 2010-03 Conspiracies 59 2013-09 Space Exploration 18 2010-04 Dungeon Fantasy III 60 2013-10 Tools of the Trade: Clerics 19 2010-05 Way of the Warrior 61 2013-11 Infinite Worlds [I] 20 2010-06 Transhuman Space II 62 2013-12 Cyberpunk 21 2010-07 Infinite Worlds II 63 2014-01 Banestorm 22 2010-08 Pirates and Swashbucklers 64 2014-02 Action Adventures 23 2010-09 Alternate GURPS III 65 2014-03 Bio-Tech 24 2010-10 The Laws of Magic 66 2014-04 Epic Magic 25 2010-11 Tools of the -

Astronomy 330 Classes Final Papers Final
Astronomy 330 Classes •! CHP allows $100 for informal get togethers. •! We are meeting Thursday to watch a movie and order some pizza. •! Still want Armageddon? Music: Space Race is Over – Billy Bragg Final Papers Final •! Final papers due on May 3rd. •! Take-home final –! At the beginning of class... •! Will email it out on the last class. •! You must turn final paper in with the graded •! Will consist of: rough draft. –! 2 large essays •! If you are happy with your rough draft grade as –! 2 short essays you final paper grade, then don’t worry about it. –! 5-8 short answers •! Due May 11th, hardcopy, by 5pm in my mailbox or office. Online ICES Outline •! What is the future for interstellar travel? •! ICES forms are available online. •! Fermi’s Paradox– Where are they? •! I appreciate you filling them out! –! In addition to campus honors thingy •! Please make sure to leave written comments. I find these comments the most useful, and typically that’s where I make the most changes to the course. Drake Equation Warp Drives Frank That’s 22,181 advanced civs!!! Drake •! Again, science fiction is influencing science. •! Due to great distance between the stars and the speed limit of c, sci-fi had to resort to “Warp Drive” that allows faster-than-light speeds. N = R* ! fp ! ne ! fl ! fi ! fc ! L •! Currently, this is impossible. # of # of •! It is speculation that requires a Star Fraction Fraction advanced Earthlike Fraction Fraction Lifetime of formation of stars that revolution in physics civilizations planets on which that evolve advanced rate with commun- we can per life arises intelligence civilizations –! It is science fiction! planets icate contact in system •! But, we have been surprised our Galaxy 6 before… today 15 0.65 1.3 x 0.1 0.125 0.175 .8 1x10 •! Unfortunately new physics usually = 0.13 intel./ comm./ yrs/ http://www.filmjerk.com/images/warp.gif stars/ systems/ life/ adds constraints not removes them. -

Location: NT-13 “Lamprey” Dyson Sphere Station (Incomplete), Edge of Terran Protectorate Shift Timestamp: 01:58 February, 30
Location: NT-13 “Lamprey” Dyson Sphere Station (Incomplete), Edge of Terran Protectorate Shift Timestamp: 01:58 February, 30, 2560 ‘The amazing part is,’ a voice in my head spoke up as I slipped through yet another set of maintenance shafts and corridors that looked exactly the same as the last ones I’d just ducked out of, ‘the whole power grid is still working.’ I nodded at that, and got back to work slapping wall mounted Security flashers onto the walls, outright using some Clown’s SUPER Glue to get the job done in as short a time as I could. It didn’t stop the robots from using the damn places, but at least it kept the more biological threats from trying their hands at rooting me out personally. Waking up in this life had been not good. … Azure ‘starlight’ seeps like syrup though cracks in the glass ceiling, through which a massive sapphire blue ‘star’ could easily be observed from the viens the station that were the maintenance halls. The floor shudders in time with the churning of machinery somewhere far beneath my feet. The air, if I were to pull off my hermetically sealed helmet off for a moment, has the strange tang of unknown chemicals and over-processed air that speaks of any space station, but the undertones of copper and something wholly unpleasant, something like rot and excrement and worse, are unique to this place. I stopped as a door opened in the distance and without even thinking I unholstered the gun from my chest sling. -
![Dyson Spheres Around White Dwarfs Arxiv:1503.04376V1 [Physics.Pop-Ph] 15 Mar 2015](https://docslib.b-cdn.net/cover/7808/dyson-spheres-around-white-dwarfs-arxiv-1503-04376v1-physics-pop-ph-15-mar-2015-597808.webp)
Dyson Spheres Around White Dwarfs Arxiv:1503.04376V1 [Physics.Pop-Ph] 15 Mar 2015
Dyson Spheres around White Dwarfs Ibrahim_ Semiz∗ and Salim O˘gury Bo˘gazi¸ciUniversity, Department of Physics Bebek, Istanbul,_ TURKEY Abstract A Dyson Sphere is a hypothetical structure that an advanced civ- ilization might build around a star to intercept all of the star's light for its energy needs. One usually thinks of it as a spherical shell about one astronomical unit (AU) in radius, and surrounding a more or less Sun-like star; and might be detectable as an infrared point source. We point out that Dyson Spheres could also be built around white dwarfs. This type would avoid the need for artificial gravity technol- ogy, in contrast to the AU-scale Dyson Spheres. In fact, we show that parameters can be found to build Dyson Spheres suitable {temperature- and gravity-wise{ for human habitation. This type would be much harder to detect. 1 Introduction The "Dyson Sphere" [1] concept is well-known in discussions of possible in- telligent life in the universe, and has even infiltrated popular culture to some extent, including being prominently featured in a Star Trek episode [2]. In its simplest version, it is a spherical shell that totally surrounds a star to intercept all of the star's light. If a Dyson Sphere (from here on, sometimes \Sphere", sometimes DS) was built around the Sun, e.g. with same radius (1 AU) as Earth's orbit (Fig. 1), it would receive all the power of the Sun, 3:8 × 1026 W, in contrast to the power intercepted by Earth, 1:7 × 1017 W. -

Science Fiction Stories with Good Astronomy & Physics
Science Fiction Stories with Good Astronomy & Physics: A Topical Index Compiled by Andrew Fraknoi (U. of San Francisco, Fromm Institute) Version 7 (2019) © copyright 2019 by Andrew Fraknoi. All rights reserved. Permission to use for any non-profit educational purpose, such as distribution in a classroom, is hereby granted. For any other use, please contact the author. (e-mail: fraknoi {at} fhda {dot} edu) This is a selective list of some short stories and novels that use reasonably accurate science and can be used for teaching or reinforcing astronomy or physics concepts. The titles of short stories are given in quotation marks; only short stories that have been published in book form or are available free on the Web are included. While one book source is given for each short story, note that some of the stories can be found in other collections as well. (See the Internet Speculative Fiction Database, cited at the end, for an easy way to find all the places a particular story has been published.) The author welcomes suggestions for additions to this list, especially if your favorite story with good science is left out. Gregory Benford Octavia Butler Geoff Landis J. Craig Wheeler TOPICS COVERED: Anti-matter Light & Radiation Solar System Archaeoastronomy Mars Space Flight Asteroids Mercury Space Travel Astronomers Meteorites Star Clusters Black Holes Moon Stars Comets Neptune Sun Cosmology Neutrinos Supernovae Dark Matter Neutron Stars Telescopes Exoplanets Physics, Particle Thermodynamics Galaxies Pluto Time Galaxy, The Quantum Mechanics Uranus Gravitational Lenses Quasars Venus Impacts Relativity, Special Interstellar Matter Saturn (and its Moons) Story Collections Jupiter (and its Moons) Science (in general) Life Elsewhere SETI Useful Websites 1 Anti-matter Davies, Paul Fireball. -

WAYS to USE SCIENCE FICTION in the SCIENCE CLASSROOM by Connie Willis, David Katz, and Courtney Willis ©1999 by Connie Willis, David Katz and Courtney Willis
WAYS TO USE SCIENCE FICTION IN THE SCIENCE CLASSROOM by Connie Willis, David Katz, and Courtney Willis ©1999 by Connie Willis, David Katz and Courtney Willis. All rights reserved. Reproduced with permission of the authors. Reproduction for classroom use must contain the original copyright. Originally presented as part of a symposium on Science and Science Fiction, National Science Teachers Association national meeting, Boston, MA, March 25-28, 1999. 1. SF can be used to teach science concepts Many stories explain and incorporate science concepts. --Arthur C. Clarke's "Silence, Please" discusses wave interference --Larry Niven's RINGWORLD shows us a Dyson sphere --the setting in Connie Willis's "The Sidon in the Mirror" is based on Harlow Shapley's theory of red giants --H. Beam Piper's "Omnilingual"'s plot revolves around the periodic table --George Gamow's MR. TOMPKINS IN PAPERBACK dreams of relativity and quantum effects --Anthologies such as THE UNIVERSE, THE PLANETS, AND THE MICROVERSE (edited by Byron Preiss) put essays by eminent scients and stories by noted sf authors side-by-side --Hal Clement, a retired high school chemistry teacher, has written a number of stories, including the classic MISSION OF GRAVITY, about all those things you learned in high school science classes. Bad science in science fiction (especially in the movies) can teach science concepts, too. --Why is it impossible for the spaceship in CAPRICORN ONE to make it back from mars in a mere three months? --Why does the strength to mass ratio make King Kong and Godzilla impossible? --What about all those loud explosions in outer space? And those spaceships that bank and turn just like fighter planes? 2. -

Long Futures and Type Iv Civilizations
PERIODICA POLYTECHNICA SER. SOC. MAN. SCI. VOL. 12, NO. 1, PP. 83–89 (2004) LONG FUTURES AND TYPE IV CIVILIZATIONS Zoltán GALÁNTAI Department of Innovation Studies and History of Technology Budapest University of Technology and Economics H–1111 Hungary, Budapest, Stoczek u. 2., bg. St., gfloor 7. Tel: (+36) 1 463–2141, Fax: (+36) 1 463–1412 e-mail: [email protected] Received: September 7, 2003 Abstract The emergence of the physical eschatology in the last decades led to an opportunity to ask questions about the fate of our Universe from a cosmologist’s point of view and to study mankind’s possible future on a cosmological scale, while we can define some theoretical limits of a civilization’s possible developments. Keywords: physical eschatology, Kardashev civilizations, Type IV civilization, criticism of Anthropic Cosmological Principle, artificial and natural signs. “Whether the details of my calculations turn out to be correct or not, I think I have shown that there are good scientific reasons for taking seriously the possibility that life and intelligence can succeed in mold- ing this universe of ours to their own purposes.” (Freeman Dyson: Time Without End: Physics and Biology in an Open Universe) 1. Introduction We could imagine a physicist floating in his laboratory in the outer space, far from any celestial body. That physicist would never discover the gravitational force without the closeness of big masses like our planet, wrote Astronomer Royal Sir Martin Rees, and similarly, the existence of some unknown forces is also imaginable, whose effects are not detectable on the scale of our Planetary System – but they would play an important role either in the centers of galaxies or in cosmology [1]. -

Front Freespace Cover.Jpg
Welcome to FreeSpace! It is my great pleasure to bring you FreeSpace – The excellent RPG designers who hang out over a free-to-use region spanning two full 8x10 hex at RPGGeek brought their love for space sectors. These system-neutral sectors can be exploration, knowledge of gaming, and massive used in any spacefaring game with at least 1 creative talent to this project. We hope you FTL capable species. The civilizations and enjoy this product and, if you do, please check worlds included in this region include cosmic out our other community created offerings anomalies, space whales, hive-minds, world- over at DriveThruRPG: builder races, militant corporatists, and https://www.drivethrurpg.com/browse/pub/10 everything in between. 397/Zoid-Enterprises Thanks for reading and feel free to leave us a rating or review! ~RPG Community Project Creation Team 1 Sample file Table of Contents: Hex: 0708 ........................................................ 45 Welcome to FreeSpace! ................................... 1 Hex: 0709 ........................................................ 59 Table of Contents: ............................................ 2 Hex: 0710 ........................................................ 60 FreeSpace Sector Map ..................................... 3 Hex: 0801 ........................................................ 61 Hex: 0101 ......................................................... 4 Hex: 0802 ........................................................ 62 Hex: 0102 ........................................................ -

A Taxonomy for Technology Producing Exobiosphere the Janus Hypothesis Jonathan Forest Byrne Rising Sun Consulting, Boston MA
A Taxonomy for Technology Producing Exobiosphere The Janus Hypothesis Jonathan Forest Byrne Rising Sun Consulting, Boston MA BSTRACTI Summary of the Janus Hypothesis he potential for matter to become self aware involves a complex interaction of variables from microcosmic Top: Energy demands for a TPB increase The hypothesis describes intelligence as a chaotic attractor through which matter evolves through to macrocosmic spatial- temporal scales within a highly specific set of boundary conditions. For example, exponentially commensurate with a transition from The Janus hypothesis is based upon the following higher states of organizational complexity. Five successive states, in turn, are marked by four distinct biospheres ( as defined by a system of decreasing net entropy that evolves from an abiotic to a biotic state) a Planetary (TPB1) to an Interplanetary (TBP 2) bifurcation points until the asymptotic limit is reached i.e. further evolution is constrained by physical in which higher trophic level organisms ( e.g. multicelluar and metazoan) results from stochastic processes assumptions stage. laws. The hypothesis also implies that rather than evolving civilizations dominating of matter (via that produce higher levels of organization in which one outcome is “intelligence” ( as defined by the ability : A Dyson Sphere may be constructed out Center construction and engineering), that matter, in fact, dominates the evolution of civilizations along of an organized system to process information via feedback loops). One product of intelligence is of materials associated with resident jovian technology that it turn becomes enmeshed within the continuum of the increasing organizational states of 1)As of the time of this writing, the number of exoplanets pathways of increasing organizational complexity. -

IN OUR OWN SOLAR SYSTEM): Searching for ET Near White Dwarfs
JBIS VOLUME 72 2019 PAGES 386–395 THERE’S NO PLACE LIKE HOME (IN OUR OWN SOLAR SYSTEM): Searching for ET Near White Dwarfs JOHN GERTZ Zorro Productions, 2249 Fifth Street, Berkeley, CA, 94710, USA Email [email protected] The preponderance of white dwarfs in the Milky Way were formed from the remnants of stars of the same or somewhat higher mass as the Sun, i.e., from G-stars. We know that life can exist around G-stars. Any technologically advanced civilization residing within the habitable zone of a G-star will face grave peril when its star transitions from the main sequence and successively enters sub-giant, red giant, planetary nebula, and white dwarf stages. In fact, if the civilization takes no action it will face certain extinction. The two alternatives to passive extinction are (a) migrate away from the parent star in order to colonize another star system, or (b) find a viable solution within one’s own solar system. It is argued in this paper that migration of an entire biological population or even a small part of a population is virtually impossible, but in any event, far more difficult than remaining in one’s home solar system where the problem of continued survival can best be solved. This leads to the conclusion that sub-giants, red giants, planetary nebula, and white dwarfs are the best possible candidate targets for SETI observations. Search strategies are suggested. Keywords: SETI, ET, World ships, White dwarf, Interstellar colonization 1 INTRODUCTION: WITH SO MANY HABITABLE PLANETS, fore “unless we discover that interstellar travel is impractical, I WHERE IS ET? conclude that we are probably alone in the Galaxy” [11]. -

D E N N I S K . C H
DENNIS K. CHAN The Story The First Thermonuclear War was not kind to the Earth. Over the last two centuries, civil unrest and climate change continued to ravage every region of the globe. Crop yields were plunging, resources were depleting, and poverty and crime were rampant. Humanity was facing extinction. The solution seemed clear: abandon Earth and find a new home among the stars. Faced with the prospect of annihilation, the remaining factions on Earth came together. On New Year’s Eve 2240, the Treaty of Scientific Exchange was signed at the old site of the Lincoln Memorial in Washington, D.C. The world’s resources were poured into spacefaring research, and all discoveries were shared on a globally distributed network. For the first time in history, humanity acted as one. In only six short years, the first hyper-spacecraft was built by the engineers of the Nishida-Østergaard Corporation under the leadership of Dr. Edmund Saito, and the technology was shared with the rest of the world. Humanity had finally entered the Spacefaring Era. Soon after this keystone discovery, other factions also researched primitive terraforming techniques, radiation-resistant crops, asteroid mining, and other key components for human survival outside the solar system. Countless exoplanet expeditions were initiated every month. Now that a solution has been found, ambition for power and control stirred in each faction once again... The Goal of the Game Beyond the Sun is a space civilization game where players collectively decide the technological progress of humankind at the dawn of the Spacefaring Era, while competing against each other to be the leading faction in economic development, science, and galactic influence.