Identifying Layout Classes for Mathematical Symbols Using Layout Context
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Gateless Gate Has Become Common in English, Some Have Criticized This Translation As Unfaithful to the Original
Wú Mén Guān The Barrier That Has No Gate Original Collection in Chinese by Chán Master Wúmén Huìkāi (1183-1260) Questions and Additional Comments by Sŏn Master Sǔngan Compiled and Edited by Paul Dōch’ŏng Lynch, JDPSN Page ii Frontspiece “Wú Mén Guān” Facsimile of the Original Cover Page iii Page iv Wú Mén Guān The Barrier That Has No Gate Chán Master Wúmén Huìkāi (1183-1260) Questions and Additional Comments by Sŏn Master Sǔngan Compiled and Edited by Paul Dōch’ŏng Lynch, JDPSN Sixth Edition Before Thought Publications Huntington Beach, CA 2010 Page v BEFORE THOUGHT PUBLICATIONS HUNTINGTON BEACH, CA 92648 ALL RIGHTS RESERVED. COPYRIGHT © 2010 ENGLISH VERSION BY PAUL LYNCH, JDPSN NO PART OF THIS BOOK MAY BE REPRODUCED OR TRANSMITTED IN ANY FORM OR BY ANY MEANS, GRAPHIC, ELECTRONIC, OR MECHANICAL, INCLUDING PHOTOCOPYING, RECORDING, TAPING OR BY ANY INFORMATION STORAGE OR RETRIEVAL SYSTEM, WITHOUT THE PERMISSION IN WRITING FROM THE PUBLISHER. PRINTED IN THE UNITED STATES OF AMERICA BY LULU INCORPORATION, MORRISVILLE, NC, USA COVER PRINTED ON LAMINATED 100# ULTRA GLOSS COVER STOCK, DIGITAL COLOR SILK - C2S, 90 BRIGHT BOOK CONTENT PRINTED ON 24/60# CREAM TEXT, 90 GSM PAPER, USING 12 PT. GARAMOND FONT Page vi Dedication What are we in this cosmos? This ineffable question has haunted us since Buddha sat under the Bodhi Tree. I would like to gracefully thank the author, Chán Master Wúmén, for his grace and kindness by leaving us these wonderful teachings. I would also like to thank Chán Master Dàhuì for his ineptness in destroying all copies of this book; thankfully, Master Dàhuì missed a few so that now we can explore the teachings of his teacher. -
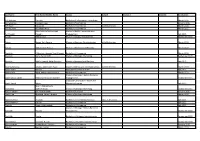
Last Name First Name/Middle Name Course Award Course 2 Award 2 Graduation
Last Name First Name/Middle Name Course Award Course 2 Award 2 Graduation A/L Krishnan Thiinash Bachelor of Information Technology March 2015 A/L Selvaraju Theeban Raju Bachelor of Commerce January 2015 A/P Balan Durgarani Bachelor of Commerce with Distinction March 2015 A/P Rajaram Koushalya Priya Bachelor of Commerce March 2015 Hiba Mohsin Mohammed Master of Health Leadership and Aal-Yaseen Hussein Management July 2015 Aamer Muhammad Master of Quality Management September 2015 Abbas Hanaa Safy Seyam Master of Business Administration with Distinction March 2015 Abbasi Muhammad Hamza Master of International Business March 2015 Abdallah AlMustafa Hussein Saad Elsayed Bachelor of Commerce March 2015 Abdallah Asma Samir Lutfi Master of Strategic Marketing September 2015 Abdallah Moh'd Jawdat Abdel Rahman Master of International Business July 2015 AbdelAaty Mosa Amany Abdelkader Saad Master of Media and Communications with Distinction March 2015 Abdel-Karim Mervat Graduate Diploma in TESOL July 2015 Abdelmalik Mark Maher Abdelmesseh Bachelor of Commerce March 2015 Master of Strategic Human Resource Abdelrahman Abdo Mohammed Talat Abdelziz Management September 2015 Graduate Certificate in Health and Abdel-Sayed Mario Physical Education July 2015 Sherif Ahmed Fathy AbdRabou Abdelmohsen Master of Strategic Marketing September 2015 Abdul Hakeem Siti Fatimah Binte Bachelor of Science January 2015 Abdul Haq Shaddad Yousef Ibrahim Master of Strategic Marketing March 2015 Abdul Rahman Al Jabier Bachelor of Engineering Honours Class II, Division 1 -

Pragmatic Analysis of English Fuzzy Language in International Business Negotiation Ling-Ling ZUO and Ying HE Ningbo Dahongying University, Ningbo, China
2016 International Conference on Education, Training and Management Innovation (ETMI 2016) ISBN: 978-1-60595-395-3 Pragmatic Analysis of English Fuzzy Language in International Business Negotiation Ling-ling ZUO and Ying HE Ningbo Dahongying University, Ningbo, China Keywords: International business negotiation, Fuzzy language, Pragmatic analysis. Abstract. This thesis aims to lead negotiators to pay more attention to use fuzzy language and put forward three strategies for negotiators to use fuzzy language in business negotiation following the cooperative principle and politeness principle. The thesis proves its importance in business negotiation by theoretical analysis and showing a series of examples. The author provides some strategies for negotiators and guides them to negotiate in international business negotiation well such as ambiguity, euphemism and so on. Sometimes, negotiators have to violate the maxims to gain a better result. The appropriate appliance of fuzzy language can relive the tension in business negotiation, being accurate and flexible, and improving the efficiency. The innovation of this paper is from the practical application of fuzzy language to better negotiation. Introduction Nowadays, with the development of economy, the communication between countries becomes closer and closer. The foreign trades are becoming more and more frequent. In order to integrate into the globalization quickly, people must pay attention to international business negotiation in the foreign trade. Business negotiation is a basic form of communication, which plays an important role in the foreign trade. Business negotiation requires negotiators not only know the rules, laws and foreign trade business very well, but also have negotiation skills. However, in real business negotiations, accurate and clear information may put one party in a worse situation. -

The Anonymity Heuristic: How Surnames Stop Identifying People When They Become Trademarks
Volume 124 Issue 2 Winter 2019 The Anonymity Heuristic: How Surnames Stop Identifying People When They Become Trademarks Russell W. Jacobs Follow this and additional works at: https://ideas.dickinsonlaw.psu.edu/dlr Part of the Behavioral Economics Commons, Civil Law Commons, Comparative and Foreign Law Commons, Economic Theory Commons, Intellectual Property Law Commons, Law and Economics Commons, Law and Psychology Commons, Legal Writing and Research Commons, Legislation Commons, Other Law Commons, Phonetics and Phonology Commons, Psychiatry and Psychology Commons, Psycholinguistics and Neurolinguistics Commons, and the Semantics and Pragmatics Commons Recommended Citation Russell W. Jacobs, The Anonymity Heuristic: How Surnames Stop Identifying People When They Become Trademarks, 124 DICK. L. REV. 319 (2020). Available at: https://ideas.dickinsonlaw.psu.edu/dlr/vol124/iss2/3 This Article is brought to you for free and open access by the Law Reviews at Dickinson Law IDEAS. It has been accepted for inclusion in Dickinson Law Review by an authorized editor of Dickinson Law IDEAS. For more information, please contact [email protected]. \\jciprod01\productn\D\DIK\124-2\DIK202.txt unknown Seq: 1 28-JAN-20 14:56 The Anonymity Heuristic: How Surnames Stop Identifying People When They Become Trademarks Russell Jacobs ABSTRACT This Article explores the following question central to trade- mark law: if a homograph has both a surname and a trademark interpretation will consumers consider those interpretations as intrinsically overlapping or the surname and trademark as com- pletely separate and unrelated words? While trademark jurispru- dence typically has approached this question from a legal perspective or with assumptions about consumer behavior, this Article builds on the Law and Behavioral Science approach to legal scholarship by drawing from the fields of psychology, lin- guistics, economics, anthropology, sociology, and marketing. -

Additional Reviewers
Additional Reviewers Rehab AbdelKader Wei Huang Jaidev Patwardhan Aneesh Aggarwal Yehea Ismail Marinus Pennings Raid Ayoub Hans Jacobson Antoniu Pop Saisanthosh Balakrishnan Renatas Jakushokas Mikhail Popovich Rajeev Balasubramonian Geert Janssen Prateek Pujara Deniz Balkan Kamil Kedziersky Fahim Rahim Chinnakrishnan Ballapuram Georgios Keramidas Wenjing Rao Ansuman Banerjee E.J. Kim Vimal Reddy Bradford Beckmann Youngmin Kim Samuel Rodriguez Gordon Bell Jingfei Kong Bogdan Romanescu Luca Benini Gurhan Kucuk Eric Rotenberg Sergey Berezin Prasad Kulkarni Barry Rountree Reinaldo Bergamaschi Christopher L. LaFrieda Silvius Rus Jannick Bergeron Johnny LeBlanc Babak Salamat Santosh Biswas Han-Lin Lee Peter Sassone Steven Burns Leonard Lee Jun Sawada Carlos A. Cabrera Wan-Ping Lee Martin Schulz Zhongbo Cao Bing Li Li Shang Guangyu Chen Tong Li Shervin Sharifi MingJing Chen Chun-Shan Lin Joseph Sharkey Tai-Chen Chen Yan Lin Montek Singh Tung-Chieh Chen Hung-Yi Liu Abhishek Somani Yi-Zong Chen Dan Lo Srikanth Srinivasan Allen C. Cheng Jiang Long Witawas Srisa-an Lei Cheng David Lowenthal Ankur Srivastava Eli Chiprout Shih-Lien Lu Christian Stangier John Chu Anita Lungu Nathan Thomas Martin Dimitrov Tony Ma Carlos Tokunaga Praveen Dua Yi Ma Nuengwong Tuaycharoen Lieven Eeckhout Francisco J. Martinez Ankush Varma Natalie Enright-Jerger Sally A. McKee Pavlos Vranas Joshua B. Fryman Albert Meixner Sarma Vrudhula Zhaohui Fu Gokhan Memik Markus Wedler Amit Gandhi Ke Meng Eric Weglarz Hongliang Gao Fayez Mohamood Paul West Michael Geiger Kartik Mohanram Polychronis Xekalakis Steven German In-Ho Moon Hua Xiang Mrinmoy Ghosh Kevin Moore Chengmo Yang Jim Grundy Miquel Moretó Matt Yourst Onur Guzey Sangeetha Nair Hui Zeng Kevin S. -

Social Mobility in China, 1645-2012: a Surname Study Yu (Max) Hao and Gregory Clark, University of California, Davis [email protected], [email protected] 11/6/2012
Social Mobility in China, 1645-2012: A Surname Study Yu (Max) Hao and Gregory Clark, University of California, Davis [email protected], [email protected] 11/6/2012 The dragon begets dragon, the phoenix begets phoenix, and the son of the rat digs holes in the ground (traditional saying). This paper estimates the rate of intergenerational social mobility in Late Imperial, Republican and Communist China by examining the changing social status of originally elite surnames over time. It finds much lower rates of mobility in all eras than previous studies have suggested, though there is some increase in mobility in the Republican and Communist eras. But even in the Communist era social mobility rates are much lower than are conventionally estimated for China, Scandinavia, the UK or USA. These findings are consistent with the hypotheses of Campbell and Lee (2011) of the importance of kin networks in the intergenerational transmission of status. But we argue more likely it reflects mainly a systematic tendency of standard mobility studies to overestimate rates of social mobility. This paper estimates intergenerational social mobility rates in China across three eras: the Late Imperial Era, 1644-1911, the Republican Era, 1912-49 and the Communist Era, 1949-2012. Was the economic stagnation of the late Qing era associated with low intergenerational mobility rates? Did the short lived Republic achieve greater social mobility after the demise of the centuries long Imperial exam system, and the creation of modern Westernized education? The exam system was abolished in 1905, just before the advent of the Republic. Exam titles brought high status, but taking the traditional exams required huge investment in a form of “human capital” that was unsuitable to modern growth (Yuchtman 2010). -

Self-Study Syllabus on Chinese Foreign Policy
Self-Study Syllabus on Chinese Foreign Policy www.mandarinsociety.org PrefaceAbout this syllabus with China’s rapid economic policymakers in Washington, Tokyo, Canberra as the scale and scope of China’s current growth, increasing military and other capitals think about responding to involvement in Africa, China’s first overseas power,Along and expanding influence, Chinese the challenge of China’s rising power. military facility in Djibouti, or Beijing’s foreign policy is becoming a more salient establishment of the Asian Infrastructure concern for the United States, its allies This syllabus is organized to build Investment Bank (AIIB). One of the challenges and partners, and other countries in Asia understanding of Chinese foreign policy in that this has created for observers of China’s and around the world. As China’s interests a step-by-step fashion based on one hour foreign policy is that so much is going on become increasingly global, China is of reading five nights a week for four weeks. every day it is no longer possible to find transitioning from a foreign policy that was In total, the key readings add up to roughly one book on Chinese foreign policy that once concerned principally with dealing 800 pages, rarely more than 40–50 pages will provide a clear-eyed assessment of with the superpowers, protecting China’s for a night. We assume no prior knowledge everything that a China analyst should know. regional interests, and positioning China of Chinese foreign policy, only an interest in as a champion of developing countries, to developing a clearer sense of how China is To understanding China’s diplomatic history one with a more varied and global agenda. -

English Versions of Chinese Authors' Names in Biomedical Journals
Dialogue English Versions of Chinese Authors’ Names in Biomedical Journals: Observations and Recommendations The English language is widely used inter- In English transliteration, two-syllable Forms of Chinese Authors’ Names nationally for academic purposes. Most of given names sometimes are spelled as two in Biomedical Journals the world’s leading life-science journals are words (Jian Hua), sometimes as one word We recently reviewed forms of Chinese published in English. A growing number (Jianhua), and sometimes hyphenated authors’ names accompanying English- of Chinese biomedical journals publish (Jian-Hua). language articles or abstracts in various abstracts or full papers in this language. Occasionally Chinese surnames are Chinese and Western biomedical journals. We have studied how Chinese authors’ two syllables (for example, Ou-Yang, Mu- We found considerable inconsistency even names are presented in English in bio- Rong, Si-Ma, and Si-Tu). Editors who are within the same journal or issue. The forms medical journals. There is considerable relatively unfamiliar with Chinese names were in the following categories: inconsistency. This inconsistency causes may mistake these compound surnames for • Surname in all capital letters followed by confusion, for example, in distinguishing given names. hyphenated or closed-up given name, for surnames from given names and thus cit- China has 56 ethnic groups. Names example, ing names properly in reference lists. of minority group members can differ KE Zhi-Yong (Chinese Journal of In the current article we begin by pre- considerably from those of Hans, who Contemporary Pediatrics) senting as background some features of constitute most of the Chinese population. GUO Liang-Qian (Chinese Chinese names. -

Table of Contents (PDF)
September 2016 JASNVol. 27 No. 9 Journal of the American Society of Nephrology This Month’s Highlights BRIEF COMMUNICATIONS 2597 MicroRNA-23b Targets Ras GTPase-Activating UP FRONT MATTERS Protein SH3 Domain-Binding Protein 2 to Alleviate Fibrosis and Albuminuria in Diabetic Editorials Nephropathy 2543 Receptor Protein Tyrosine Phosphatase g,CO2 Binghai Zhao, Hongzhi Li, Jieting Liu, Pengfei Han, Sensing in Proximal Tubule and Acid Base Chunlei Zhang, He Bai, Xiaohuan Yuan, Xiaoli Wang, Homeostasis Li Li, Hongchuang Ma, Xiudong Jin, and Yanhui Chu Manoocher Soleimani · See related article by Zhou et al. (pp. 2616–2621). 2609 Recombinant N–Terminal Slit2 Inhibits TGF-b–Induced Fibroblast Activation and 2545 Glucocorticoid-Regulated Kinase: Linking Renal Fibrosis Azotemia and Muscle Wasting in CKD Darren A. Yuen, Yi-Wei Huang, Guang-Ying Liu, Madhav C. Menon and John Cijiang He Sajedabanu Patel, Fei Fang, Joyce Zhou, Kerri Thai, · See related article by Luo et al. (pp. 2797–2808). Ahmad Sidiqi, Stephen G. Szeto, Lauren Chan, Mingliang Lu, Xiaolin He, Rohan John, Richard E. 2547 Challenges in Rare Variant Association Studies Gilbert, James W. Scholey, and Lisa A. Robinson for Complex Kidney Traits: CFHR5 and IgA Nephropathy 2616 Role of Receptor Protein Tyrosine Phosphatase g 2 Krzysztof Kiryluk in Sensing Extracellular CO2 and HCO3 · See related article by Zhai et al. (pp. 2894–2905). Yuehan Zhou, Lara A. Skelton, Lumei Xu, Margaret P. Chandler, Jessica M. Berthiaume, and Walter F. Boron 2551 The Search for a Biomarker of Relapse in · See related editorial by Soleimani (pp. 2543–2545). ANCA-Associated Vasculitis Meghan E. Free and Ronald J. -

Names of Chinese People in Singapore
101 Lodz Papers in Pragmatics 7.1 (2011): 101-133 DOI: 10.2478/v10016-011-0005-6 Lee Cher Leng Department of Chinese Studies, National University of Singapore ETHNOGRAPHY OF SINGAPORE CHINESE NAMES: RACE, RELIGION, AND REPRESENTATION Abstract Singapore Chinese is part of the Chinese Diaspora.This research shows how Singapore Chinese names reflect the Chinese naming tradition of surnames and generation names, as well as Straits Chinese influence. The names also reflect the beliefs and religion of Singapore Chinese. More significantly, a change of identity and representation is reflected in the names of earlier settlers and Singapore Chinese today. This paper aims to show the general naming traditions of Chinese in Singapore as well as a change in ideology and trends due to globalization. Keywords Singapore, Chinese, names, identity, beliefs, globalization. 1. Introduction When parents choose a name for a child, the name necessarily reflects their thoughts and aspirations with regards to the child. These thoughts and aspirations are shaped by the historical, social, cultural or spiritual setting of the time and place they are living in whether or not they are aware of them. Thus, the study of names is an important window through which one could view how these parents prefer their children to be perceived by society at large, according to the identities, roles, values, hierarchies or expectations constructed within a social space. Goodenough explains this culturally driven context of names and naming practices: Department of Chinese Studies, National University of Singapore The Shaw Foundation Building, Block AS7, Level 5 5 Arts Link, Singapore 117570 e-mail: [email protected] 102 Lee Cher Leng Ethnography of Singapore Chinese Names: Race, Religion, and Representation Different naming and address customs necessarily select different things about the self for communication and consequent emphasis. -

Surname Methodology in Defining Ethnic Populations : Chinese
Surname Methodology in Defining Ethnic Populations: Chinese Canadians Ethnic Surveillance Series #1 August, 2005 Surveillance Methodology, Health Surveillance, Public Health Division, Alberta Health and Wellness For more information contact: Health Surveillance Alberta Health and Wellness 24th Floor, TELUS Plaza North Tower P.O. Box 1360 10025 Jasper Avenue, STN Main Edmonton, Alberta T5J 2N3 Phone: (780) 427-4518 Fax: (780) 427-1470 Website: www.health.gov.ab.ca ISBN (on-line PDF version): 0-7785-3471-5 Acknowledgements This report was written by Dr. Hude Quan, University of Calgary Dr. Donald Schopflocher, Alberta Health and Wellness Dr. Fu-Lin Wang, Alberta Health and Wellness (Authors are ordered by alphabetic order of surname). The authors gratefully acknowledge the surname review panel members of Thu Ha Nguyen and Siu Yu, and valuable comments from Yan Jin and Shaun Malo of Alberta Health & Wellness. They also thank Dr. Carolyn De Coster who helped with the writing and editing of the report. Thanks to Fraser Noseworthy for assisting with the cover page design. i EXECUTIVE SUMMARY A Chinese surname list to define Chinese ethnicity was developed through literature review, a panel review, and a telephone survey of a randomly selected sample in Calgary. It was validated with the Canadian Community Health Survey (CCHS). Results show that the proportion who self-reported as Chinese has high agreement with the proportion identified by the surname list in the CCHS. The surname list was applied to the Alberta Health Insurance Plan registry database to define the Chinese ethnic population, and to the Vital Statistics Death Registry to assess the Chinese ethnic population mortality in Alberta. -

Student Intake Surname Given Names 1 Citizenship Fall 2015 LIN Yung
Student Intake Surname Given names 1 Citizenship Fall 2015 LIN Yung-Chun Taiwan Fall 2015 LEUNG Sung Hei Hong Kong Fall 2012 ABRAHAM Akshay India Fall 2015 ADIWINATA Theresa Indonesia Winter 2012 AL MAHDI Majid Saudi Arabia Fall 2015 ALNAQEH Sultan United Arab Emirates Winter 2012 ALQASSEM Marwan United Arab Emirates Fall 2013 ALSHAMSI Fares Khamis United Arab Emirates Winter 2014 AMIN Saqib Pakistan Fall 2015 ANAND Tarun India Fall 2014 AO Lin China Winter 2015 ASMARA Jildra Annisa Indonesia Fall 2015 AUNG Win Phyu Myanmar Winter 2014 AYE May Phyu Myanmar Fall 2012 MOHD AZMI Mariam Malaysia Winter 2015 BAI Chenguang China Fall 2012 BAI Yue China Fall 2013 BAO Yikun China Summer 2011 BATMUNKH Manlai Mongolia Winter 2012 BEIGI Shahriar Iran Fall 2014 BIDZHIEVA Ksenia Russian Federation Fall 2015 BINSALMA Faisal United Arab Emirates Fall 2015 BO Gin Gar Myanmar Fall 2014 BUBNOV Nikita Russian Federation Fall 2013 CAI Liming China Fall 2012 CAI Mengting China Summer 2014 CAI Pengcheng China Summer 2014 CAI Qing China Winter 2014 CAI Zhiwen China Fall 2013 CAO Fangyan China Fall 2013 CAO Ruijia China Winter 2014 CAO Yaning China Fall 2014 CAO Yiming China Fall 2015 CAO Zhengxiong China Fall 2013 CHAN Hoi Chi Hong Kong Fall 2013 CHANG Hang China Winter 2015 CHAO Hsin-Yu Taiwan Fall 2012 SINGH Chandan India Winter 2014 CHAU Venus Hong Kong Fall 2011 CHAN Yulun Taiwan Fall 2014 CHEN Bohan China Fall 2011 CHEN Chun China Fall 2014 CHEN Changzhen China Fall 2014 CHEN Guanqiu China Fall 2015 CHEN Huan China Winter 2014 CHEN Haoran China Fall 2014