Environmental Modeling Under Uncertainty: Monte Carlo Simulation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
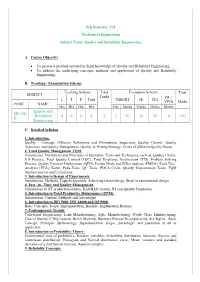
D Quality and Reliability Engineering 4 0 0 4 4 3 70 30 20 0
B.E Semester: VII Mechanical Engineering Subject Name: Quality and Reliability Engineering A. Course Objective To present a problem oriented in depth knowledge of Quality and Reliability Engineering. To address the underlying concepts, methods and application of Quality and Reliability Engineering. B. Teaching / Examination Scheme Teaching Scheme Total Evaluation Scheme Total SUBJECT Credit PR. / L T P Total THEORY IE CIA VIVO Marks CODE NAME Hrs Hrs Hrs Hrs Hrs Marks Marks Marks Marks Quality and ME706- Reliability 4 0 0 4 4 3 70 30 20 0 120 D Engineering C. Detailed Syllabus 1. Introduction: Quality – Concept, Different Definitions and Dimensions, Inspection, Quality Control, Quality Assurance and Quality Management, Quality as Wining Strategy, Views of different Quality Gurus. 2. Total Quality Management TQM: Introduction, Definitions and Principles of Operation, Tools and Techniques, such as, Quality Circles, 5 S Practice, Total Quality Control (TQC), Total Employee Involvement (TEI), Problem Solving Process, Quality Function Deployment (QFD), Failure Mode and Effect analysis (FMEA), Fault Tree Analysis (FTA), Kizen, Poka-Yoke, QC Tools, PDCA Cycle, Quality Improvement Tools, TQM Implementation and Limitations. 3. Introduction to Design of Experiments: Introduction, Methods, Taguchi approach, Achieving robust design, Steps in experimental design 4. Just –in –Time and Quality Management: Introduction to JIT production system, KANBAN system, JIT and Quality Production. 5. Introduction to Total Productive Maintenance (TPM): Introduction, Content, Methods and Advantages 6. Introduction to ISO 9000, ISO 14000 and QS 9000: Basic Concepts, Scope, Implementation, Benefits, Implantation Barriers 7. Contemporary Trends: Concurrent Engineering, Lean Manufacturing, Agile Manufacturing, World Class Manufacturing, Cost of Quality (COQ) system, Bench Marking, Business Process Re-engineering, Six Sigma - Basic Concept, Principle, Methodology, Implementation, Scope, Advantages and Limitation of all as applicable. -

Quality Assurance: Best Practices in Clinical SAS® Programming
NESUG 2012 Management, Administration and Support Quality Assurance: Best Practices in Clinical SAS® Programming Parag Shiralkar eClinical Solutions, a Division of Eliassen Group Abstract SAS® programmers working on clinical reporting projects are often under constant pressure of meeting tight timelines, producing best quality SAS® code and of meeting needs of customers. As per regulatory guidelines, a typical clinical report or dataset generation using SAS® software is considered as software development. Moreover, since statistical reporting and clinical programming is a part of clinical trial processes, such processes are required to follow strict quality assurance guidelines. While SAS® programmers completely focus on getting best quality deliverable out in a timely manner, quality assurance needs often get lesser priorities or may get unclearly understood by clinical SAS® programming staff. Most of the quality assurance practices are often focused on ‘process adherence’. Statistical programmers using SAS® software and working on clinical reporting tasks need to maintain adequate documentation for the processes they follow. Quality control strategy should be planned prevalently before starting any programming work. Adherence to standard operating procedures, maintenance of necessary audit trails, and necessary and sufficient documentation are key aspects of quality. This paper elaborates on best quality assurance practices which statistical programmers working in pharmaceutical industry are recommended to follow. These quality practices -

Data Quality Monitoring and Surveillance System Evaluation
TECHNICAL DOCUMENT Data quality monitoring and surveillance system evaluation A handbook of methods and applications www.ecdc.europa.eu ECDC TECHNICAL DOCUMENT Data quality monitoring and surveillance system evaluation A handbook of methods and applications This publication of the European Centre for Disease Prevention and Control (ECDC) was coordinated by Isabelle Devaux (senior expert, Epidemiological Methods, ECDC). Contributing authors John Brazil (Health Protection Surveillance Centre, Ireland; Section 2.4), Bruno Ciancio (ECDC; Chapter 1, Section 2.1), Isabelle Devaux (ECDC; Chapter 1, Sections 3.1 and 3.2), James Freed (Public Health England, United Kingdom; Sections 2.1 and 3.2), Magid Herida (Institut for Public Health Surveillance, France; Section 3.8 ), Jana Kerlik (Public Health Authority of the Slovak Republic; Section 2.1), Scott McNabb (Emory University, United States of America; Sections 2.1 and 3.8), Kassiani Mellou (Hellenic Centre for Disease Control and Prevention, Greece; Sections 2.2, 2.3, 3.3, 3.4 and 3.5), Gerardo Priotto (World Health Organization; Section 3.6), Simone van der Plas (National Institute of Public Health and the Environment, the Netherlands; Chapter 4), Bart van der Zanden (Public Health Agency of Sweden; Chapter 4), Edward Valesco (Robert Koch Institute, Germany; Sections 3.1 and 3.2). Project working group members: Maria Avdicova (Public Health Authority of the Slovak Republic), Sandro Bonfigli (National Institute of Health, Italy), Mike Catchpole (Public Health England, United Kingdom), Agnes -

Quality Control and Reliability Engineering 1152Au128 3 0 0 3
L T P C QUALITY CONTROL AND RELIABILITY ENGINEERING 1152AU128 3 0 0 3 1. Preamble This course provides the essentiality of SQC, sampling and reliability engineering. Study on various types of control charts, six sigma and process capability to help the students understand various quality control techniques. Reliability engineering focuses on the dependability, failure mode analysis, reliability prediction and management of a system 2. Pre-requisite NIL 3. Course Outcomes Upon the successful completion of the course, learners will be able to Level of learning CO Course Outcomes domain (Based on Nos. C01 Explain the basic concepts in Statistical Process Control K2 Apply statistical sampling to determine whether to accept or C02 K2 reject a production lot Predict lifecycle management of a product by applying C03 K2 reliability engineering techniques. C04 Analyze data to determine the cause of a failure K2 Estimate the reliability of a component by applying RDB, C05 K2 FMEA and Fault tree analysis. 4. Correlation with Programme Outcomes Cos PO1 PO2 PO3 PO4 PO5 PO6 PO7 PO8 PO9 PO10 PO11 PO12 PSO1 PSO2 CO1 H H H M L H M L CO2 H H H M L H H M CO3 H H H M L H L H CO4 H H H M L H M M CO5 H H H M L H L H H- High; M-Medium; L-Low 5. Course content UNIT I STATISTICAL QUALITY CONTROL L-9 Methods and Philosophy of Statistical Process Control - Control Charts for Variables and Attributes Cumulative Sum and Exponentially Weighted Moving Average Control Charts - Other SPC Techniques Process - Capability Analysis - Six Sigma Concept. -

Statistical Quality Control Methods in Infection Control and Hospital Epidemiology, Part I: Introduction and Basic Theory Author(S): James C
Statistical Quality Control Methods in Infection Control and Hospital Epidemiology, Part I: Introduction and Basic Theory Author(s): James C. Benneyan Source: Infection Control and Hospital Epidemiology, Vol. 19, No. 3 (Mar., 1998), pp. 194-214 Published by: The University of Chicago Press Stable URL: http://www.jstor.org/stable/30143442 Accessed: 25/06/2010 18:26 Your use of the JSTOR archive indicates your acceptance of JSTOR's Terms and Conditions of Use, available at http://www.jstor.org/page/info/about/policies/terms.jsp. JSTOR's Terms and Conditions of Use provides, in part, that unless you have obtained prior permission, you may not download an entire issue of a journal or multiple copies of articles, and you may use content in the JSTOR archive only for your personal, non-commercial use. Please contact the publisher regarding any further use of this work. Publisher contact information may be obtained at http://www.jstor.org/action/showPublisher?publisherCode=ucpress. Each copy of any part of a JSTOR transmission must contain the same copyright notice that appears on the screen or printed page of such transmission. JSTOR is a not-for-profit service that helps scholars, researchers, and students discover, use, and build upon a wide range of content in a trusted digital archive. We use information technology and tools to increase productivity and facilitate new forms of scholarship. For more information about JSTOR, please contact [email protected]. The University of Chicago Press is collaborating with JSTOR to digitize, preserve and extend access to Infection Control and Hospital Epidemiology. -

Methodological Challenges Associated with Meta-Analyses in Health Care and Behavioral Health Research
o title: Methodological Challenges Associated with Meta Analyses in Health Care and Behavioral Health Research o date: May 14, 2012 Methodologicalo author: Challenges Associated with Judith A. Shinogle, PhD, MSc. Meta-AnalysesSenior Research Scientist in Health , Maryland InstituteCare for and Policy Analysis Behavioraland Research Health Research University of Maryland, Baltimore County 1000 Hilltop Circle Baltimore, Maryland 21250 http://www.umbc.edu/mipar/shinogle.php Judith A. Shinogle, PhD, MSc Senior Research Scientist Maryland Institute for Policy Analysis and Research University of Maryland, Baltimore County 1000 Hilltop Circle Baltimore, Maryland 21250 http://www.umbc.edu/mipar/shinogle.php Please see http://www.umbc.edu/mipar/shinogle.php for information about the Judith A. Shinogle Memorial Fund, Baltimore, MD, and the AKC Canine Health Foundation (www.akcchf.org), Raleigh, NC. Inquiries may also be directed to Sara Radcliffe, Executive Vice President for Health, Biotechnology Industry Organization, www.bio.org, 202-962-9200. May 14, 2012 Methodological Challenges Associated with Meta-Analyses in Health Care and Behavioral Health Research Judith A. Shinogle, PhD, MSc I. Executive Summary Meta-analysis is used to inform a wide array of questions ranging from pharmaceutical safety to the relative effectiveness of different medical interventions. Meta-analysis also can be used to generate new hypotheses and reflect on the nature and possible causes of heterogeneity between studies. The wide range of applications has led to an increase in use of meta-analysis. When skillfully conducted, meta-analysis is one way researchers can combine and evaluate different bodies of research to determine the answers to research questions. However, as use of meta-analysis grows, it is imperative that the proper methods are used in order to draw meaningful conclusions from these analyses. -

University Quality Indicators: a Critical Assessment
DIRECTORATE GENERAL FOR INTERNAL POLICIES POLICY DEPARTMENT B: STRUCTURAL AND COHESION POLICIES CULTURE AND EDUCATION UNIVERSITY QUALITY INDICATORS: A CRITICAL ASSESSMENT STUDY This document was requested by the European Parliament's Committee on Culture and Education AUTHORS Bernd Wächter (ACA) Maria Kelo (ENQA) Queenie K.H. Lam (ACA) Philipp Effertz (DAAD) Christoph Jost (DAAD) Stefanie Kottowski (DAAD) RESPONSIBLE ADMINISTRATOR Mr Miklós Györffi Policy Department B: Structural and Cohesion Policies European Parliament B-1047 Brussels E-mail: [email protected] EDITORIAL ASSISTANCE Lyna Pärt LINGUISTIC VERSIONS Original: EN ABOUT THE EDITOR To contact the Policy Department or to subscribe to its monthly newsletter please write to: [email protected] Manuscript completed in April 2015. © European Parliament, 2015. Print ISBN 978-92-823-7864-9 doi: 10.2861/660770 QA-02-15-583-EN-C PDF ISBN 978-92-823-7865-6 doi: 10.2861/426164 QA-02-15-583-EN-N This document is available on the Internet at: http://www.europarl.europa.eu/studies DISCLAIMER The opinions expressed in this document are the sole responsibility of the author and do not necessarily represent the official position of the European Parliament. Reproduction and translation for non-commercial purposes are authorized, provided the source is acknowledged and the publisher is given prior notice and sent a copy. DIRECTORATE GENERAL FOR INTERNAL POLICIES POLICY DEPARTMENT B: STRUCTURAL AND COHESION POLICIES CULTURE AND EDUCATION UNIVERSITY QUALITY INDICATORS: A CRITICAL ASSESSMENT STUDY Abstract The ‘Europe 2020 Strategy’ and other EU initiatives call for more excellence in Europe’s higher education institutions in order to improve their performance, international attractiveness and competitiveness. -

Assessment of Clinical Trial Quality and Its Impact on Meta-Analyses
Rev Saúde Pública 2005;39(6):865-73 865 www.fsp.usp.br/rsp Avaliação da qualidade de estudos clínicos e seu impacto nas metanálises Assessment of clinical trial quality and its impact on meta-analyses Carlos Rodrigues da Silva Filhoa, Humberto Saconatob, Lucieni Oliveira Conternoa, Iara Marquesb e Álvaro Nagib Atallahc aFaculdade Estadual de Medicina de Marília. Marília, SP, Brasil. bUniversidade Federal do Rio Grande do Norte. Natal, RN, Brasil. cEscola Paulista de Medicina. Universidade Federal de São Paulo. São Paulo, SP, Brasil Descritores Resumo Ensaios controlados aleatórios. Garantia de qualidade dos cuidados de Objetivo saúde. Questionários. Avaliação de Analisar se diferentes instrumentos de avaliação de qualidade, aplicados a um grupo resultados, cuidados de saúde. de estudos clínicos que se correlacionam e qual seu impacto no resultado na metanálise. Controle de qualidade. Métodos Foram analisados 38 estudos clínicos randomizados e controlados, selecionados para a revisão sistemática sobre a eficácia terapêutica do Interferon Alfa no tratamento da hepatite crônica pelo vírus B. Utilizaram-se os seguintes instrumentos: Maastricht (M), Delphi (D) e Jadad (J) e o método da Colaboração Cochrane (CC), considerado padrão-ouro. Os resultados definidos pelos três instrumentos foram comparados pelo teste de Correlação de Spearman. O teste de Kappa (K) avaliou a concordância entre os revisores na aplicação dos instrumentos e o teste de Kappa ponderado analisou o ordenamento de qualidade definido pelos instrumentos. O clareamento do HBV- DNA e HbeAg foi o desfecho avaliado na metanálise. Resultados Os estudos foram de regular e baixa qualidade. A concordância entre os revisores foi, de acordo com o instrumento: D=0.12, J=0.29 e M=0.33 e CC= 0,53. -

Quality Assurance/Quality Control Officer Is a Fully-Experienced, Single-Position Classification
Class Code: Quality Assurance/Quality Control 460 Officer DEFINITION Under direction from the Director of Operations and Maintenance, performs a key role in maintaining the District’s State environmental laboratory accreditation; develops, directs, and coordinates a comprehensive quality assurance/quality control (QA/QC) program for staff involved in the collection and analysis of water samples; develops and coordinates special programs and projects related to quality control with a variety of District supervisors and federal, state, and local agencies; reviews and implements laboratory practices and procedures that conform to District and regulatory quality assurance and safety standards for environmental laboratories; prepares a variety of routine reports and develops and maintains a program standards manual and computer based programs for quality control, statistical analysis, report generation, and related activities; and performs related work as required. DISTINGUISHING CHARACTERISTICS The Quality Assurance/Quality Control Officer is a fully-experienced, single-position classification. Under general direction, within a framework of policies and procedures, the incumbent has specific responsibility for the development, direction, and coordination of a comprehensive QA/QC program for use in the Headquarters Laboratory, satellite laboratories, and the field to ensure high quality analytical results. Assignments are given in broad terms and subject to review upon completion by the Director of Operations and Maintenance. There is considerable -

On the Reproducibility of Meta-Analyses: Six Practical Recommendations
UvA-DARE (Digital Academic Repository) On the reproducibility of meta-analyses six practical recommendations Lakens, D.; Hilgard, J.; Staaks, J. DOI 10.1186/s40359-016-0126-3 Publication date 2016 Document Version Final published version Published in BMC Psychology License CC BY Link to publication Citation for published version (APA): Lakens, D., Hilgard, J., & Staaks, J. (2016). On the reproducibility of meta-analyses: six practical recommendations. BMC Psychology, 4, [24]. https://doi.org/10.1186/s40359-016- 0126-3 General rights It is not permitted to download or to forward/distribute the text or part of it without the consent of the author(s) and/or copyright holder(s), other than for strictly personal, individual use, unless the work is under an open content license (like Creative Commons). Disclaimer/Complaints regulations If you believe that digital publication of certain material infringes any of your rights or (privacy) interests, please let the Library know, stating your reasons. In case of a legitimate complaint, the Library will make the material inaccessible and/or remove it from the website. Please Ask the Library: https://uba.uva.nl/en/contact, or a letter to: Library of the University of Amsterdam, Secretariat, Singel 425, 1012 WP Amsterdam, The Netherlands. You will be contacted as soon as possible. UvA-DARE is a service provided by the library of the University of Amsterdam (https://dare.uva.nl) Download date:25 Sep 2021 Lakens et al. BMC Psychology (2016) 4:24 DOI 10.1186/s40359-016-0126-3 DEBATE Open Access On the reproducibility of meta-analyses: six practical recommendations Daniël Lakens1*, Joe Hilgard2 and Janneke Staaks3 Abstract Background: Meta-analyses play an important role in cumulative science by combining information across multiple studies and attempting to provide effect size estimates corrected for publication bias. -

Content Sheet 7-1: Overview of Quality Control for Quantitative Tests
Content Sheet 7-1: Overview of Quality Control for Quantitative Tests Role in Quality Control (QC) is a component quality of process control, and is a major Organization Personnel Equipment management element of the quality management system system. It monitors the processes related to the examination phase of testing and allows for detecting errors Purchasing Process Information & Control Management in the testing system. These errors may Inventory be due to test system failure, adverse environmental conditions, or operator performance. QC gives the laboratory Documents Occurrence & Management Assessment confidence that test results are accurate Records and reliable before patient results are reported. This module explains how quality Process Customer Facilities Improvement Service & control methods are applied to Safety quantitative laboratory examinations. Overview of Quantitative tests measure the quantity of a substance in a sample, yielding a numeric the process result. For example, the quantitative test for glucose can give a result of 110 mg/dL. Since quantitative tests have numeric values, statistical tests can be applied to the results of quality control material to differentiate between test runs that are “in control” and “out of control”. This is done by calculating acceptable limits for control material, then testing the control with the patient’s samples to see if it falls within established limits. As a part of the quality management system, the laboratory must establish a quality control program for all quantitative tests. -

Control Charts and Trend Analysis for ISO/IEC 17025:2005
QMS Quick Learning Activity Controls and Control Charting Control Charts and Trend Analysis for ISO/IEC 17025:2005 www.aphl.org Abbreviation and Acronyms • CRM-Certified Reference Materials • RM-Reference Materials • PT-Proficiency Test(ing) • QMS-Quality Management Sytem • QC-Quality Control • STD-Standard Deviation • Ct-cycle threshold QMS Quick Learning Activity ISO/IEC 17025 Requirements Section 5.9 - Assuring the quality of test results and calibration results • quality control procedures for monitoring the validity of tests undertaken • data recorded so trends are detected • where practicable, statistical techniques applied to the reviewing of the results QMS Quick Learning Activity ISO/IEC 17025 Requirements Monitoring • Planned • Reviewed • May include o Use of Certified Reference Materials (CRM) and/or Reference Materials (RM) o Proficiency testing (PT) o Replicate tests o Retesting o Correlation of results for different characteristics QMS Quick Learning Activity Quality Management System (QMS) The term ‘Quality Management System’ covers the quality, technical, and administrative system that governs the operations of the laboratory. The laboratory’s QMS will have procedures for monitoring the validity of tests and calibrations undertaken in the laboratory. QMS Quick Learning Activity Quality Management System (QMS) Quality Manual may state: The laboratory monitors the quality of test results by the inclusion of quality control measures in the performance of tests and participation in proficiency testing programs. The laboratory