DOCSLIB.ORG

Fundamentals and Applications of the Monte Carlo Method

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Fundamentals and Applications of the Monte Carlo Method -JC-PT6S-63-C>2 fundamentals and Applications of the Monte Carlo Method By E. STOIAN* (16th A71n'/url Technical llIeeting, The Petroleum Society of C.l_ill" Calgm'y, May, 1.?65) ABSTRACT The Monte Carlo method embarked on a course of Perhaps no industry is more vitally concerned with risk its own when calculations using random numbers than the oil and gas industry, and few professional men were s}'stematical!:r considered as a di::itinct topic uf other than petroleum engineers are required to recom­ studJ' by S. Wilks (19441- mend higher investments on the basis of such uncertain Downloaded from http://onepetro.org/jcpt/article-pdf/4/03/120/2166363/petsoc-65-03-02.pdf by guest on 25 September 2021 and limited information. Tn recent }'ears, the number of The picturesque name of Monte Carlo originuted al methods dealing with risk and uncertainty has grown the Los Alamos Scientific Laboratory with von N eu­ extensh-el}' so that the classical approach, using ana­ mann and Ulam (194--1) as a code for cla~sified worl{ lytical procedures and single-yalued parameters, has un­ dergone a significant transformation. The use of stochas­ related to the simulation of neutron behaviour. tic "ariables, such as those frequentl,r encountered in the The novelty of the Monte Carlo method lies chiefly oil industry, is now economically feasible in the eyulua­ tion of an increasing number of problems by the applica~ in the unexpected approach. l\Iore specifically, the tion of Monte Carlo techniques. Ile'wne~s relates to the suggestion that many relation­ This paper defines the Monte Carlo method as a subset ships arising in non-probabilistic contexts can be of simulation techniques and a combination of sampling evaluated more easily by stochastic experiments than theory and numerical analysis_ Briefly, the basic tech­ by standard anal:rtical methods. This, in effect. is the nique of Monte Carlo simulation inyob.-es the represen­ tation of a situation in log-ical terms so that, when the von Neumann - Ulam concept. pertinent data are inserted, a mathematical solution be­ The difficulty of accepting Monte Carlu solution::! comes Jlossible. Using random numbers generated by an "automatic penny-tossing machine" and a cumulatiye fre­ as ans\...·er::! in science and engineering is, independent Quency distribution, the beha'\'iour pattern of the particu­ of legal supedicial aspects, not to be underestimated. lar case can be determined by a process of statistical ex­ Certain signg, however, are promising. Indeed, the perimentation_ In practical applications, the probabilistic Monte Carlo techniques have received considerable data expressed in one or several distributions may pertain to geological exploration, discover).' processes, oil-in~place publicity in the paRt fifteen yean.; and the method haH e\'aluations or the productivity of heterogeneous reser­ recently attained a statLl~ of preliminar.r acceptance, Yoirs. The great variety of probabilit).' models used to Extensive references exist on both general and :;pe­ date (e..[_, normal, log-normal, skewed log~normal, linear, multi-modal, discontinuous, theoretical, experimental) con­ cific topics (1, 2). The Monte Carlo method, however, firms a broad range of experimental computations and a is still unfamiliar to those direct1)r concerned with g-enuine interest in realistic representations of random potential applications. More particularly. the method impacts encountered in practice. is seldom Llsed by petroleum engineers (3, 4). This Emphasis in this paper is directed to the salient charac­ teristics of the Monte Cado method, with particular ref­ paper has been prepared to stimulate intereRt in the erence to applications in areas related to the oil and ,gas Monte Carlo method and its applications in the oil nnd industry_ Attention is focused on reservoir engin{'erin~ gas industry. The intention is to present a deal' pic­ models. Nevertheless. management facets of the oil and ture of the method and its tools in order to provide gas business are considered alan,!! with other applications in statistics, mathematics, physics and engineering. Sam­ a "feeling" foL' recognition of applications as they oc­ ple size reducing techniques and the use of digital com· cur in practice. puters are also discussed. DEFINITION INTRODUCTION The Monte Carlo method may be defined <"8 a means HE Monte Carlo method may have originated of design and study of a stochastic model which simu­ T with a mathematician wishing to know ho\\o" many lates, in all essential aspects, a physical OL' mathema­ gteps a drunkard would have to take to get a speci­ tical proces.s. Basically, the method is one of numer­ fied distance away from a tavern, assuming that ical integration. As a combination of gampling theoLT each of his steps had an equal probability of being and numerical analysis, the fi'1onte Carlo method is a cast in any of the four principal directions. This lead~ special contL·ibution to the science of computing, Brief­ to the classic concept of "random walk" which has ly, Monte Carlo is a practical method which HotVCH great problem-solving potential. problems by numerical operations on random num­ Another classical principle is associated with Buf­ bel"S, Some experts apply the name Monte Carlo only fon (1773), who observed that if a plane is ruled to cases that are best illustrated by the use of prob­ with parallel and equally spaced lines, and a needle abilistic techniques to solve nonstatistical mathema­ just long enough to reach from one line to the next is tical problems, Other experts reserve the Monte Carlo thrown at random, the probability that the needle de5ignation onlJr for calculations implementing sophis­ crosses a line is 2/.". This leads to the important dis­ ticated variance-reducing techniques. cover~r that one can evaluate a definite quantity by a Statistical sampling procedures and must llumel'ical completel~r random process. experiments of a stochastic nature (i.e., involving a seL of ordered observations) are now included in the Monte Carlo method, and it is in this context that '''''Oil u?ld Gas COlllim·uation Board, Calgary, Alta. the name "I\'ionte Carlo" will be used, 120 The Journal of Canadian Petroleum --'- -- --,..: , ' BASIC TECHNIQUES. Concept of Ran~omness The important st~p-s in ~ lV~onte Carlo calculation The idea of mathematical randomness is that "in are: the long run" such-and-such conditions will "almost .(l)-Selecting or designing a probability model by always" prevail. ·By way of illustration, in the long statistical data reduction, analogy 01' theoretic.al con­ run approximately half of the tosses of a true coin siderations. would be -heads. Statisticians associate randomness (2)-Generating random numbers and correspond­ with probability. The "intuitive" school states that randomness must be defined with reference to "in­ ing random variables. stantaneous" probability and not to what ,~'ill happen (3)-Designing and implementing variance-reduc­ "in the long run." The proponents of the "frequency" ing techniques. theory define both randomness and probability in terms of the frequency hypothesis of equal probabili­ SALIENT CHARACTERISTICS ties. The "short term" and the "long run" may be as­ ,~ sumed to be two facets of probability; namely, the '. Drawing from various publications (1, 2). the sali­ subjecti,'e and objective probabilitYl respectively.. ent characteristics of the Monte Carlo method appear 1; to be as follows; Att1"ibutes of Pseudo-Random.. Numbe1·s (I)-The Monte Carlo' method is associated with Downloaded from http://onepetro.org/jcpt/article-pdf/4/03/120/2166363/petsoc-65-03-02.pdf by guest on 25 September 2021 probability theory_ However, whereas the relation­ Most processes of generating random numbers are ships -of probability theory have been derived from cyclic. If the cycle is relatively long for a specific ap­ theoretical considerations of the phenomenon of plication) however, the sequence can be considered .chance, the Monte Carlo method uses probability to "locally random" for all practical purposes. This con­ find answers to physical problems that maJ~ or may cept is very profitable in that we can use simple not be related to probability. processes to generate pseudo-random numbers for I i (2)-The application of the Monte Carlo method of­ practical applications. To qualify for pseudo-random­ l fers a penetrating insight into the behaviour of the ness, sequences must comply with certain require­ s~ystems studied. Frequently, problems become decep­ ments. Some of these are ~ tively simple. In this sense, effective Monte Carlo (a). In any sequence, the digits used in the num­ techniques are self-liquidating. bers must be distributed with uniform density; Le_. (3)-The results of Monte Carlo computations are they must be iu roughly equal quantities. treated as estimates within certain confidence limits (b). Successive digits must be uncorrelated; i.e.• rather than true or exact values. Actually, all mean­ no digit should tend to follow any other digit. ingful physical measurements are expressed in this (c). There must be no correlation between succes­ way. In many cases where relationships in a model sive numbers_ cannot be evaluated at all because of either mathe­ Tests of randomness apply to the generating process matical or practical considerations, Monte Carlo tech­ rather than the randomness of the sequence. Common niques can be used to obtain approximations. tests are: (a) Frequency; (b) Serial; (c) Poker; and (4)-As in any other method, there is a need for (d) Gap Tests. Additionally, there are independence, adequate basic information; data for the implemen­ normality and chi-square tests. tation of the Monte Cado method, however, may be b~r obtained standard rlata processing procedures. SOU1·ce of Random Sequences (5)-The method is flexible to the extent that the intricacies of a problem. as may be reflected by either Random numbers may be obtained bi: (a) a phys­ a great number of parameters or complicated geo­ ical process, (b) "look-up" in a formal table and (c) metry, do not alter its basic character; the penalty digital computers.
Load more

Recommended publications
  • Programming in Stata
    Programming and Post-Estimation • Bootstrapping • Monte Carlo • Post-Estimation Simulation (Clarify) • Extending Clarify to Other Models – Censored Probit Example What is Bootstrapping? • A computer-simulated nonparametric technique for making inferences about a population parameter based on sample statistics. • If the sample is a good approximation of the population, the sampling distribution of interest can be estimated by generating a large number of new samples from the original. • Useful when no analytic formula for the sampling distribution is available. B 2 ˆ B B b How do I do it? SE B = s(x )- s(x )/ B /(B -1) å[ åb =1 ] b=1 1. Obtain a Sample from the population of interest. Call this x = (x1, x2, … , xn). 2. Re-sample based on x by randomly sampling with replacement from it. 3. Generate many such samples, x1, x2, …, xB – each of length n. 4. Estimate the desired parameter in each sample, s(x1), s(x2), …, s(xB). 5. For instance the bootstrap estimate of the standard error is the standard deviation of the bootstrap replications. Example: Standard Error of a Sample Mean Canned in Stata use "I:\general\PRISM Programming\auto.dta", clear Type: sum mpg Example: Standard Error of a Sample Mean Canned in Stata Type: bootstrap "summarize mpg" r(mean), reps(1000) » 21.2973±1.96*.6790806 x B - x Example: Difference of Medians Test Type: sum length, detail Type: return list Example: Difference of Medians Test Example: Difference of Medians Test Example: Difference of Medians Test Type: bootstrap "mymedian" r(diff), reps(1000) The medians are not very different.
    [Show full text]
  • The Cascade Bayesian Approach: Prior Transformation for a Controlled Integration of Internal Data, External Data and Scenarios
    risks Article The Cascade Bayesian Approach: Prior Transformation for a Controlled Integration of Internal Data, External Data and Scenarios Bertrand K. Hassani 1,2,3,* and Alexis Renaudin 4 1 University College London Computer Science, 66-72 Gower Street, London WC1E 6EA, UK 2 LabEx ReFi, Université Paris 1 Panthéon-Sorbonne, CESCES, 106 bd de l’Hôpital, 75013 Paris, France 3 Capegemini Consulting, Tour Europlaza, 92400 Paris-La Défense, France 4 Aon Benfield, The Aon Centre, 122 Leadenhall Street, London EC3V 4AN, UK; [email protected] * Correspondence: [email protected]; Tel.: +44-(0)753-016-7299 Received: 14 March 2018; Accepted: 23 April 2018; Published: 27 April 2018 Abstract: According to the last proposals of the Basel Committee on Banking Supervision, banks or insurance companies under the advanced measurement approach (AMA) must use four different sources of information to assess their operational risk capital requirement. The fourth includes ’business environment and internal control factors’, i.e., qualitative criteria, whereas the three main quantitative sources available to banks for building the loss distribution are internal loss data, external loss data and scenario analysis. This paper proposes an innovative methodology to bring together these three different sources in the loss distribution approach (LDA) framework through a Bayesian strategy. The integration of the different elements is performed in two different steps to ensure an internal data-driven model is obtained. In the first step, scenarios are used to inform the prior distributions and external data inform the likelihood component of the posterior function. In the second step, the initial posterior function is used as the prior distribution and the internal loss data inform the likelihood component of the second posterior function.
    [Show full text]
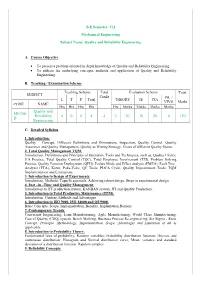
  • D Quality and Reliability Engineering 4 0 0 4 4 3 70 30 20 0
    B.E Semester: VII Mechanical Engineering Subject Name: Quality and Reliability Engineering A. Course Objective To present a problem oriented in depth knowledge of Quality and Reliability Engineering. To address the underlying concepts, methods and application of Quality and Reliability Engineering. B. Teaching / Examination Scheme Teaching Scheme Total Evaluation Scheme Total SUBJECT Credit PR. / L T P Total THEORY IE CIA VIVO Marks CODE NAME Hrs Hrs Hrs Hrs Hrs Marks Marks Marks Marks Quality and ME706- Reliability 4 0 0 4 4 3 70 30 20 0 120 D Engineering C. Detailed Syllabus 1. Introduction: Quality – Concept, Different Definitions and Dimensions, Inspection, Quality Control, Quality Assurance and Quality Management, Quality as Wining Strategy, Views of different Quality Gurus. 2. Total Quality Management TQM: Introduction, Definitions and Principles of Operation, Tools and Techniques, such as, Quality Circles, 5 S Practice, Total Quality Control (TQC), Total Employee Involvement (TEI), Problem Solving Process, Quality Function Deployment (QFD), Failure Mode and Effect analysis (FMEA), Fault Tree Analysis (FTA), Kizen, Poka-Yoke, QC Tools, PDCA Cycle, Quality Improvement Tools, TQM Implementation and Limitations. 3. Introduction to Design of Experiments: Introduction, Methods, Taguchi approach, Achieving robust design, Steps in experimental design 4. Just –in –Time and Quality Management: Introduction to JIT production system, KANBAN system, JIT and Quality Production. 5. Introduction to Total Productive Maintenance (TPM): Introduction, Content, Methods and Advantages 6. Introduction to ISO 9000, ISO 14000 and QS 9000: Basic Concepts, Scope, Implementation, Benefits, Implantation Barriers 7. Contemporary Trends: Concurrent Engineering, Lean Manufacturing, Agile Manufacturing, World Class Manufacturing, Cost of Quality (COQ) system, Bench Marking, Business Process Re-engineering, Six Sigma - Basic Concept, Principle, Methodology, Implementation, Scope, Advantages and Limitation of all as applicable.
    [Show full text]
  • What Is Bayesian Inference? Bayesian Inference Is at the Core of the Bayesian Approach, Which Is an Approach That Allows Us to Represent Uncertainty As a Probability
    Learn to Use Bayesian Inference in SPSS With Data From the National Child Measurement Programme (2016–2017) © 2019 SAGE Publications Ltd. All Rights Reserved. This PDF has been generated from SAGE Research Methods Datasets. SAGE SAGE Research Methods Datasets Part 2019 SAGE Publications, Ltd. All Rights Reserved. 2 Learn to Use Bayesian Inference in SPSS With Data From the National Child Measurement Programme (2016–2017) Student Guide Introduction This example dataset introduces Bayesian Inference. Bayesian statistics (the general name for all Bayesian-related topics, including inference) has become increasingly popular in recent years, due predominantly to the growth of evermore powerful and sophisticated statistical software. However, Bayesian statistics grew from the ideas of an English mathematician, Thomas Bayes, who lived and worked in the first half of the 18th century and have been refined and adapted by statisticians and mathematicians ever since. Despite its longevity, the Bayesian approach did not become mainstream: the Frequentist approach was and remains the dominant means to conduct statistical analysis. However, there is a renewed interest in Bayesian statistics, part prompted by software development and part by a growing critique of the limitations of the null hypothesis significance testing which dominates the Frequentist approach. This renewed interest can be seen in the incorporation of Bayesian analysis into mainstream statistical software, such as, IBM® SPSS® and in many major statistics text books. Bayesian Inference is at the heart of Bayesian statistics and is different from Frequentist approaches due to how it views probability. In the Frequentist approach, probability is the product of the frequency of random events occurring Page 2 of 19 Learn to Use Bayesian Inference in SPSS With Data From the National Child Measurement Programme (2016–2017) SAGE SAGE Research Methods Datasets Part 2019 SAGE Publications, Ltd.
    [Show full text]
  • Basic Econometrics / Statistics Statistical Distributions: Normal, T, Chi-Sq, & F
    Basic Econometrics / Statistics Statistical Distributions: Normal, T, Chi-Sq, & F Course : Basic Econometrics : HC43 / Statistics B.A. Hons Economics, Semester IV/ Semester III Delhi University Course Instructor: Siddharth Rathore Assistant Professor Economics Department, Gargi College Siddharth Rathore guj75845_appC.qxd 4/16/09 12:41 PM Page 461 APPENDIX C SOME IMPORTANT PROBABILITY DISTRIBUTIONS In Appendix B we noted that a random variable (r.v.) can be described by a few characteristics, or moments, of its probability function (PDF or PMF), such as the expected value and variance. This, however, presumes that we know the PDF of that r.v., which is a tall order since there are all kinds of random variables. In practice, however, some random variables occur so frequently that statisticians have determined their PDFs and documented their properties. For our purpose, we will consider only those PDFs that are of direct interest to us. But keep in mind that there are several other PDFs that statisticians have studied which can be found in any standard statistics textbook. In this appendix we will discuss the following four probability distributions: 1. The normal distribution 2. The t distribution 3. The chi-square (␹2 ) distribution 4. The F distribution These probability distributions are important in their own right, but for our purposes they are especially important because they help us to find out the probability distributions of estimators (or statistics), such as the sample mean and sample variance. Recall that estimators are random variables. Equipped with that knowledge, we will be able to draw inferences about their true population values.
    [Show full text]
  • Quality Assurance: Best Practices in Clinical SAS® Programming
    NESUG 2012 Management, Administration and Support Quality Assurance: Best Practices in Clinical SAS® Programming Parag Shiralkar eClinical Solutions, a Division of Eliassen Group Abstract SAS® programmers working on clinical reporting projects are often under constant pressure of meeting tight timelines, producing best quality SAS® code and of meeting needs of customers. As per regulatory guidelines, a typical clinical report or dataset generation using SAS® software is considered as software development. Moreover, since statistical reporting and clinical programming is a part of clinical trial processes, such processes are required to follow strict quality assurance guidelines. While SAS® programmers completely focus on getting best quality deliverable out in a timely manner, quality assurance needs often get lesser priorities or may get unclearly understood by clinical SAS® programming staff. Most of the quality assurance practices are often focused on ‘process adherence’. Statistical programmers using SAS® software and working on clinical reporting tasks need to maintain adequate documentation for the processes they follow. Quality control strategy should be planned prevalently before starting any programming work. Adherence to standard operating procedures, maintenance of necessary audit trails, and necessary and sufficient documentation are key aspects of quality. This paper elaborates on best quality assurance practices which statistical programmers working in pharmaceutical industry are recommended to follow. These quality practices
    [Show full text]
  • Practical Meta-Analysis -- Lipsey & Wilson Overview
    Practical Meta-Analysis -- Lipsey & Wilson The Great Debate • 1952: Hans J. Eysenck concluded that there were no favorable Practical Meta-Analysis effects of psychotherapy, starting a raging debate • 20 years of evaluation research and hundreds of studies failed David B. Wilson to resolve the debate American Evaluation Association • 1978: To proved Eysenck wrong, Gene V. Glass statistically Orlando, Florida, October 3, 1999 aggregate the findings of 375 psychotherapy outcome studies • Glass (and colleague Smith) concluded that psychotherapy did indeed work • Glass called his method “meta-analysis” 1 2 The Emergence of Meta-Analysis The Logic of Meta-Analysis • Ideas behind meta-analysis predate Glass’ work by several • Traditional methods of review focus on statistical significance decades testing – R. A. Fisher (1944) • Significance testing is not well suited to this task • “When a number of quite independent tests of significance have been made, it sometimes happens that although few or none can be – highly dependent on sample size claimed individually as significant, yet the aggregate gives an – null finding does not carry to same “weight” as a significant impression that the probabilities are on the whole lower than would often have been obtained by chance” (p. 99). finding • Source of the idea of cumulating probability values • Meta-analysis changes the focus to the direction and – W. G. Cochran (1953) magnitude of the effects across studies • Discusses a method of averaging means across independent studies – Isn’t this what we are
    [Show full text]
  • Data Quality Monitoring and Surveillance System Evaluation
    TECHNICAL DOCUMENT Data quality monitoring and surveillance system evaluation A handbook of methods and applications www.ecdc.europa.eu ECDC TECHNICAL DOCUMENT Data quality monitoring and surveillance system evaluation A handbook of methods and applications This publication of the European Centre for Disease Prevention and Control (ECDC) was coordinated by Isabelle Devaux (senior expert, Epidemiological Methods, ECDC). Contributing authors John Brazil (Health Protection Surveillance Centre, Ireland; Section 2.4), Bruno Ciancio (ECDC; Chapter 1, Section 2.1), Isabelle Devaux (ECDC; Chapter 1, Sections 3.1 and 3.2), James Freed (Public Health England, United Kingdom; Sections 2.1 and 3.2), Magid Herida (Institut for Public Health Surveillance, France; Section 3.8 ), Jana Kerlik (Public Health Authority of the Slovak Republic; Section 2.1), Scott McNabb (Emory University, United States of America; Sections 2.1 and 3.8), Kassiani Mellou (Hellenic Centre for Disease Control and Prevention, Greece; Sections 2.2, 2.3, 3.3, 3.4 and 3.5), Gerardo Priotto (World Health Organization; Section 3.6), Simone van der Plas (National Institute of Public Health and the Environment, the Netherlands; Chapter 4), Bart van der Zanden (Public Health Agency of Sweden; Chapter 4), Edward Valesco (Robert Koch Institute, Germany; Sections 3.1 and 3.2). Project working group members: Maria Avdicova (Public Health Authority of the Slovak Republic), Sandro Bonfigli (National Institute of Health, Italy), Mike Catchpole (Public Health England, United Kingdom), Agnes
    [Show full text]
  • Statistical Power in Meta-Analysis Jin Liu University of South Carolina - Columbia
    University of South Carolina Scholar Commons Theses and Dissertations 12-14-2015 Statistical Power in Meta-Analysis Jin Liu University of South Carolina - Columbia Follow this and additional works at: https://scholarcommons.sc.edu/etd Part of the Educational Psychology Commons Recommended Citation Liu, J.(2015). Statistical Power in Meta-Analysis. (Doctoral dissertation). Retrieved from https://scholarcommons.sc.edu/etd/3221 This Open Access Dissertation is brought to you by Scholar Commons. It has been accepted for inclusion in Theses and Dissertations by an authorized administrator of Scholar Commons. For more information, please contact [email protected]. STATISTICAL POWER IN META-ANALYSIS by Jin Liu Bachelor of Arts Chongqing University of Arts and Sciences, 2009 Master of Education University of South Carolina, 2012 Submitted in Partial Fulfillment of the Requirements For the Degree of Doctor of Philosophy in Educational Psychology and Research College of Education University of South Carolina 2015 Accepted by: Xiaofeng Liu, Major Professor Christine DiStefano, Committee Member Robert Johnson, Committee Member Brian Habing, Committee Member Lacy Ford, Senior Vice Provost and Dean of Graduate Studies © Copyright by Jin Liu, 2015 All Rights Reserved. ii ACKNOWLEDGEMENTS I would like to express my thanks to all committee members who continuously supported me in the dissertation work. My dissertation chair, Xiaofeng Liu, always inspired and trusted me during this study. I could not finish my dissertation at this time without his support. Brian Habing helped me with R coding and research design. I could not finish the coding process so quickly without his instruction. I appreciate the encouragement from Christine DiStefano and Robert Johnson.
    [Show full text]
  • Descriptive Statistics Frequency Distributions and Their Graphs
    Chapter 2 Descriptive Statistics § 2.1 Frequency Distributions and Their Graphs Frequency Distributions A frequency distribution is a table that shows classes or intervals of data with a count of the number in each class. The frequency f of a class is the number of data points in the class. Class Frequency, f 1 – 4 4 LowerUpper Class 5 – 8 5 Limits 9 – 12 3 Frequencies 13 – 16 4 17 – 20 2 Larson & Farber, Elementary Statistics: Picturing the World , 3e 3 1 Frequency Distributions The class width is the distance between lower (or upper) limits of consecutive classes. Class Frequency, f 1 – 4 4 5 – 1 = 4 5 – 8 5 9 – 5 = 4 9 – 12 3 13 – 9 = 4 13 – 16 4 17 – 13 = 4 17 – 20 2 The class width is 4. The range is the difference between the maximum and minimum data entries. Larson & Farber, Elementary Statistics: Picturing the World , 3e 4 Constructing a Frequency Distribution Guidelines 1. Decide on the number of classes to include. The number of classes should be between 5 and 20; otherwise, it may be difficult to detect any patterns. 2. Find the class width as follows. Determine the range of the data, divide the range by the number of classes, and round up to the next convenient number. 3. Find the class limits. You can use the minimum entry as the lower limit of the first class. To find the remaining lower limits, add the class width to the lower limit of the preceding class. Then find the upper class limits. 4.
    [Show full text]
  • Quality Control and Reliability Engineering 1152Au128 3 0 0 3
    L T P C QUALITY CONTROL AND RELIABILITY ENGINEERING 1152AU128 3 0 0 3 1. Preamble This course provides the essentiality of SQC, sampling and reliability engineering. Study on various types of control charts, six sigma and process capability to help the students understand various quality control techniques. Reliability engineering focuses on the dependability, failure mode analysis, reliability prediction and management of a system 2. Pre-requisite NIL 3. Course Outcomes Upon the successful completion of the course, learners will be able to Level of learning CO Course Outcomes domain (Based on Nos. C01 Explain the basic concepts in Statistical Process Control K2 Apply statistical sampling to determine whether to accept or C02 K2 reject a production lot Predict lifecycle management of a product by applying C03 K2 reliability engineering techniques. C04 Analyze data to determine the cause of a failure K2 Estimate the reliability of a component by applying RDB, C05 K2 FMEA and Fault tree analysis. 4. Correlation with Programme Outcomes Cos PO1 PO2 PO3 PO4 PO5 PO6 PO7 PO8 PO9 PO10 PO11 PO12 PSO1 PSO2 CO1 H H H M L H M L CO2 H H H M L H H M CO3 H H H M L H L H CO4 H H H M L H M M CO5 H H H M L H L H H- High; M-Medium; L-Low 5. Course content UNIT I STATISTICAL QUALITY CONTROL L-9 Methods and Philosophy of Statistical Process Control - Control Charts for Variables and Attributes Cumulative Sum and Exponentially Weighted Moving Average Control Charts - Other SPC Techniques Process - Capability Analysis - Six Sigma Concept.
    [Show full text]
  • Flood Frequency Analysis Using Copula with Mixed Marginal Distributions
    Flood frequency analysis using copula with mixed marginal distributions Project Report, Aug. 2007 Project Report August 2007 - 1 - Flood frequency analysis using copula with mixed marginal distributions Project Report, Aug. 2007 Prepared by and - 2 - Flood frequency analysis using copula with mixed marginal distributions Project Report, Aug. 2007 Abstract...................................................................................................................7 I. Introduction......................................................................................................8 II. Nonparametric method of estimating marginal distribution.................................14 II.1 Univariate kernel density estimation...........................................................14 II.2 Orthonormal series method.......................................................................17 III. The copula function.........................................................................................19 IV. Multivariate flood frequency analysis................................................................23 IV.1 Details of the case study............................................................................25 IV.2 Associations among flood characteristics.....................................................26 IV.3 Marginal distributions of flood characteristics..............................................29 IV.3.1 Parametric estimation.........................................................................30 IV.3.2 Nonparametric estimation...................................................................32
    [Show full text]