DOCSLIB.ORG

UNIT 3 DENSITY STRUCTURE S and ISOTOPES What Is Density and How to Use It?

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
UNIT 3 DENSITY STRUCTURE S and ISOTOPES What Is Density and How to Use It? UNIT 3 DENSITY STRUCTURE S AND ISOTOPES What is density and how to use it? A Brief History of Chemistry Structure of an Atom How to make Ions? What are Isotopes? DENSITY Density: is the mass of a substance per unit volume, or how much it weighs per given volume UNITS are g/cm3, g/mL, or g/L Intensive property Density = mass ÷ volume You must identify if you are using this equation opposed to dimensional analysis (write the equation out) Use the correct units for the equation PROPER UNITS FOR DENSITY All masses must be in grams (g) If not in base unit convert all masses into the base unit of grams through dimensional analysis Volume must be in milliliters (mL) for liquids, cubic centimeters (cm3) for solids, and Liters (L) for gases Use dimensional analysis to convert to desired units *** A milliliter (mL) and cubic centimeter (cm3) are the same amount*** DENSITY TRIANGLE There are three possible variable that you may have to solve fore in density problems When given 2 of them it makes it extremely easy to solve for the third When trying to figure out which form of the density equation to use: cover up what you are looking for and the 2 units left and the sign between them shows you how to solve for it. EX 3-1: WHAT IS THE DENSITY OF AN OBJECT WITH A VOLUME OF 35.7 CM3 AND WEIGHT OF 85 g? Bonus: Is this a solid, liquid, or not enough information to know? EX 3-2: IF THE DENSITY OF GOLD 19.3 g/cm3 WHAT IS THE VOLUME OF 200 g OF GOLD? EX 3-3: THE DENSITY OF LIQUID MERCURY IS 13.6 g/mL. HOW MUCH WOULD 35 mL OF MERCURY WEIGH (IN GRAMS AND POUNDS)? Hint: 1 pound = 453.59 grams EX 3-4: AN EMPTY GRADUATED CYLINDER WEIGHS 26.5 g. WHEN IT IS FILLED WITH AN UNKNOWN LIQUID TO THE 45.8 mL MARK THE NEW WEIGHT OF BOTH THE GRADUATED CYLINDER AND THE UNKNOWN LIQUID IS 70 g. WHAT IS THE DENSITY OF THE UNKNOWN LIQUID? Hint: Put the differences in masses in your equation there should be a m1 and m2. EX 3-5: A RECTANGULAR SOLIDS HAS THE DIMENSIONS FOR 3.4” BY 1.2” BY1.7” AND WEIGHS 1,500Kg. WHAT IS THE DENSITY Hint:1 in3 = 2.54 cm3 DENSITY OF WATER Memorize the specific density of water!!!! 1.0 g/mL This means 1.0 gram of water has a volume of 1.0 mL and 1.0m mL of water weights 1.0 gram This is only true at one temperature: 3.98º C Substance that has a density less then water will float in it and ones with a heaver density will sink EX 3-6: HOW MUCH DOES 500mL OF WATER WEIGH IN GRAMS? 1.0 L? Hint: Use density of water to figure this one out EX 3-7: A CERTAIN SUBSTANCE HAS A MASS OF 3.2 kg AND A VOLUME OF 1.5 ft3. IF IT DOESN'T REACT WITH THE WATER, WOULD YOU EXPECT IT TO FLOAT OR SINK? Hint: Remember to convert all units to appropriate units 1 ft3 = 12 in3 1 in3 = 254 cm3 SPECIFIC GRAVITY Specific Gravity: of a substance is the density of the substance compared to the density of a designated standard (water) If you divide the specific gravity to our standard’s (water) density. You will get the same number as the specific gravity Specific Gravity is unitless and Density has units EX 3-8: MILK HAS A SPECIFIC GRAVITY OF 1.12. HOW MUCH WOULD 1 GALLON OF MILK WEIGH IN GRAMS AND POUNDS? Hint: Convert Volume First 1 gal = 4 qt 1 L = 1.06 qt then mL to L Use specific gravity in density equation 1 lb = 454 g BRIEF HISTORY Democritus- an ancient Greek, 400 B.C. He hypothesisxed that matter could be subdivided again and again until ir reaches particles that cannot divide. Other words, he was the first to suggest the existences of the atom. John Dalton: first to develop and publish a theory about how atoms look and behave. JOHN DALTON’S ATOMIC THEORY 1. All elements are composed of small particles called atoms that are indivisible 2. All atoms of the same element are identical. (not true today because of Isotopes) 3. Atoms of different elements are different. 4. Atoms of different elements can combine with each other only in simple whole number ratios to form compounds 5. Chemical reactions occur when atoms are separated, joined or rearranged ERNEST RUTHERFORD Gold Foil Experiment - the atom was mostly space and that all positive charges were located in a very small central nucleus The Rutherford Gold Foil experiment shot minute particles at a thin sheet of gold. It was found that a small percentage of the particles were deflected, while a majority passed through the sheet. This caused Rutherford to conclude that the mass of an atom was concentrated at its center along with its protons. https://youtu.be/5pZj0u_XMbc MORE HISTORY Niels Bohr- A Danish scientist who was the first to suggest the “planetary model” of the atom. Meaning the electrons orbited the nucleus like the planets orbit the sun. Max Planck- A German Physicist who expanded and modified Bohr’s model. He theorized and proved with the quantum mechanical model that electrons do not actually “orbit” the nucleus but are found only in definite areas based on the amount of energy they have. This theory holds true today ATOMS Atom- The smallest unit of matter that still retains the properties of an element Each element consist of a certain type of atom different from the atoms of any other element (every type of atom is different) Atoms make up all matter! SUBATOMIC PARTICLES Atoms are made up of three types of particles containing a “charge” Protons (+) These are found in the nucleus it is much larger then an electron Electrons (-) These are found outside the nucleus in the what is called the “electron” cloud Neutrons (neutral) these are found in the nucleus it is the same size as a proton but no charge. ELECTRONS Electrons orient themselves around atoms in different levels called Electron Shells The outer most shell is called the Valence Shell The electrons on the outermost layer “Valence Shell” are called Valence Electrons SUBATOMIC PARTICLES Most atoms are neutrally charged # of Electrons = # of Protons Protons and Neutrons are packed densely in the middle or core of the atom this is called the Atomic Nucleus Electrons are located in the outer rings of the nucleus or electron cloud ATOMIC NUMBER AND MASS All atoms of the same element have the same number of protons in their nuclei Atomic Number - the number of protons that is unique to an element it can also represent the number of electrons in a neutral atom Atomic Mass - Average masses of all the isotopes of that particular element weighted by their percentage of abundance (the units are atomic mass units) Mass Number - sum of the protons and neutrons in the nebulous WHEN USING ATOMIC MASS IN EQUATIONS: Atomic Mass = (% isotope 1)(mass of #1) + (% isotope2)(mass of #2) + etc. Even though you are finding an average know that you do not divide by the number of isotopes. You must either change your percentage to a decimal before putting them into your equation EX 3.9: NATURALLY OCCURRING CHLORINE IS 75.53% CHLORINE-35 AND 24.47% CHLORINE-37. WHAT IS THE AVERAGE ATOMIC MASS THAT SHOULD BE PLACED ON THE PERIODIC TABLE? EX 3-10: WHAT ARE THE ATOMIC #, ATOMIC MASS, PROTON #, & ELECTRON #? EX 3-11: WHAT ARE THE ATOMIC #, # OF PROTONS, AND # OF ELECTRONS FOR EACH OF THESE ELEMENTS? Nitrogen (N) Oxygen (O) Neon (Ne) Potassium (K) EX 3-12: NAME THE NEUTRAL ELEMENTS WITH THIS MANY PROTONS: 16 72 5 19 25 CHARGED PARTICLES A non-neutral atom is called a charged particle. The particle can either be positively or negatively charged. With charged particle you can only gain and loose electrons If the particle is positively charged it has less electrons then protons and vise versa is you have a negatively charged particle When writhing out an element that is charge you wright out the element as you would normally would then out beside it as an exponent wright the charge of the particle with a (-) for negative charges and a (+) for positive charges Mg+2 C-1 EX 3-13: WHAT PARTICLE HAS A +2 CHARGE AND 12 PROTONS? EX 3-14: WHAT PARTICLE HAS A -3 CHARGE AND 33 PROTONS? How many electrons are in this charged particle? EX 3-15: WHAT PARTICLE HAS 50 PROTONS AND 48 ELECTRONS? ISOTOPE All atoms of a given element have the same number of protons but some atoms have more neutrons then other atoms of the same element thus they have greater mass. These elements are called Isotopes 12C 13C A Radioactive Isotope is one in which the nucleus days spontaneously giving off particles and energy TYPES OF BONDS Bonding is how 2 or more 4 Types elements come together Covalent Bonds to form a compound Ionic Bonds Some bonds are stronger Hydrogen Bonds then others (ex: covalent Van der Waals bonds are much stronger Interactions then hydrogen bonds) STRONG VS. WEAK CHEMICAL BONDING Strong Bonds: Weak Bonds: Covalent Hydrogen Ionic Van der Walls Interactions COVALENT BONDS Covalent Bonds happen when valence electrons are being shared between 2 atoms equally This is a very strong bond but the strength of the bonds are dictated by how many pairs of valence electrons are being shared Single bonds have one pair of valance electrons being shared Double bonds have 2 pairs of valance electrons being shared Triple Bonds have 3 pairs of valance electrons being shared IONIC BONDS Ionic bonds happen when there is unequal sharing of valance electrons Because of unequal sharing one atom becomes more negative while the other atom becomes more positive Ions- Charged atoms Cation is the positively charged ion Anion is the negatively charged ion Ionic bonding must have both an anion and cation HYDROGEN BONDING Hydrogen bonds- When an hydrogen atom is already bound to make a compound and it exerts an attraction on other elements or compounds These bonds are individually weak but can add up and make many strong bonds VAN DER WAALS INTERACTIONS These are interactions between compounds and their charge orientations (opposites attract) .
Load more

Recommended publications
  • Atomic Weights and Isotopic Abundances*
    Pure&App/. Chem., Vol. 64, No. 10, pp. 1535-1543, 1992. Printed in Great Britain. @ 1992 IUPAC INTERNATIONAL UNION OF PURE AND APPLIED CHEMISTRY INORGANIC CHEMISTRY DIVISION COMMISSION ON ATOMIC WEIGHTS AND ISOTOPIC ABUNDANCES* 'ATOMIC WEIGHT' -THE NAME, ITS HISTORY, DEFINITION, AND UNITS Prepared for publication by P. DE BIEVRE' and H. S. PEISER2 'Central Bureau for Nuclear Measurements (CBNM), Commission of the European Communities-JRC, B-2440 Geel, Belgium 2638 Blossom Drive, Rockville, MD 20850, USA *Membership of the Commission for the period 1989-1991 was as follows: J. R. De Laeter (Australia, Chairman); K. G. Heumann (FRG, Secretary); R. C. Barber (Canada, Associate); J. CCsario (France, Titular); T. B. Coplen (USA, Titular); H. J. Dietze (FRG, Associate); J. W. Gramlich (USA, Associate); H. S. Hertz (USA, Associate); H. R. Krouse (Canada, Titular); A. Lamberty (Belgium, Associate); T. J. Murphy (USA, Associate); K. J. R. Rosman (Australia, Titular); M. P. Seyfried (FRG, Associate); M. Shima (Japan, Titular); K. Wade (UK, Associate); P. De Bi&vre(Belgium, National Representative); N. N. Greenwood (UK, National Representative); H. S. Peiser (USA, National Representative); N. K. Rao (India, National Representative). Republication of this report is permitted without the need for formal IUPAC permission on condition that an acknowledgement, with full reference together with IUPAC copyright symbol (01992 IUPAC), is printed. Publication of a translation into another language is subject to the additional condition of prior approval from the relevant IUPAC National Adhering Organization. ’Atomic weight‘: The name, its history, definition, and units Abstract-The widely used term “atomic weight” and its acceptance within the international system for measurements has been the subject of debate.
    [Show full text]
  • Nuclear Criticality Safety Engineer Training Module 1 1
    Nuclear Criticality Safety Engineer Training Module 1 1 Introductory Nuclear Criticality Physics LESSON OBJECTIVES 1) to introduce some background concepts to engineers and scientists who do not have an educational background in nuclear engineering, including the basic ideas of moles, atom densities, cross sections and nuclear energy release; 2) to discuss the concepts and mechanics of nuclear fission and the definitions of fissile and fissionable nuclides. NUCLEAR CRITICALITY SAFETY The American National Standard for Nuclear Criticality Safety in Operations with Fissionable Materials Outside Reactors, ANSI/ANS-8.1 includes the following definition: Nuclear Criticality Safety: Protection against the consequences of an inadvertent nuclear chain reaction, preferably by prevention of the reaction. Note the words: nuclear - related to the atomic nucleus; criticality - can it be controlled, will it run by itself; safety - protection of life and property. DEFINITIONS AND NUMBERS What is energy? Energy is the ability to do work. What is nuclear energy? Energy produced by a nuclear reaction. What is work? Work is force times distance. 1 Developed for the U. S. Department of Energy Nuclear Criticality Safety Program by T. G. Williamson, Ph.D., Westinghouse Safety Management Solutions, Inc., in conjunction with the DOE Criticality Safety Support Group. NCSET Module 1 Introductory Nuclear Criticality Physics 1 of 18 Push a car (force) along a road (distance) and the car has energy of motion, or kinetic energy. Climb (force) a flight of steps (distance) and you have energy of position relative to the first step, or potential energy. Jump down the stairs or out of a window and the potential energy is changed to kinetic energy as you fall.
    [Show full text]
  • Answer Key Chapter 6: Standard Review Worksheet 1
    Answer Key Chapter 6: Standard Review Worksheet 1. 1 amu = 1.66 _ 10–24 g. For example, the average atomic mass of sodium is 22.99 amu, which represents the average mass of all the sodium atoms in the world (including all the various isotopes and their relative abundances). So that we will be able to use the mass of a sample of sodium to count the number of atoms of sodium present in the sample, we consider that every sodium atom in a sample has exactly the same mass (the average atomic mass). The average atomic mass of an element is typically not a whole number of amu’s because of the presence of the different isotopes of the element, each with its own relative abundance. Since the relative abundance of an element can be any number, when the weighted average atomic mass of the element is calculated, the average is unlikely to be a whole number. 2. On a microscopic basis, one mole of a substance represents Avogadro’s number (6.022 _ 1023) of individual units (atoms or molecules) of the substance. On a macroscopic basis, one mole of a substance represents the amount of substance present when the molar mass of the substance in grams is taken (for example, 12.01 g of carbon will be one mole of carbon). 3. The molar mass of a compound is the mass in grams of one mole of the compound (6.022 _ 1023 molecules of the compound) and is calculated by summing the average atomic masses of all the atoms present in a molecule of the compound.
    [Show full text]
  • 5.1: Atomic Mass Unit 5.1: Atomic Mass
    Topic 5: Stoichiometry - Chemical Arithmetic Masses of some atoms: 1 -24 16 -23 1H = 1.6736×10 g 8 O = 2.6788 ×10 g 238 -22 92U = 3.9851×10 g Introducing…….the Atomic Mass Unit (amu) 1 amu = 1.66054 x 10-24 g 1 5.1: Atomic Mass Unit Atomic Mass is defined relative to Carbon -12 isotope 12 12 amu is the mass of the 6 C isotope of carbon Carbon -12 atom = 12.000 amu Hydrogen -1 atom = 1.008 amu Oxygen -16 atom = 15.995 amu Chlorine -35 atom = 34.969 amu 2 5.1: Atomic Mass - Natural Abundance We deal with the naturally occurring mix of isotopes, rather than pure isotopes Carbon has three natural isotopes Isotope Mass (amu) Abundance (%) 12C 12.000 98.892 13C 13.00335 1.108 14C 14.00317 1 x 10-4 Any shovelful of Carbon from living material will have a Naturally Occurring Abundance of 98.892% 12C, 1.108% 13C and 0.0001% 14C 3 1 5.1: Atomic Mass - Relative Abundance How do we take into account the naturally occurring Abundances? Take the average mass of the various isotopes weighted according to their Relative Abundances Relative Isotope Mass (amu) Abundance (%) Abundance 12C 12.000 98.892 0.98892 13C 13.00335 1.108 0.0108 -6 14C 14.00317 1 x 10-4 1 x 10 N.B. The % Abundance adds up to 100 The Relative Abundance adds up to 1 4 5.1: Average Atomic Mass Relative Isotope Mass (amu) Abundance (%) Abundance 12C 12.000 98.892 0.98892 13C 13.00335 1.108 0.0108 -6 14C 14.00317 1 x 10-4 1 x 10 The Average Atomic Mass is given by: (0.98892 x 12.000 amu) + (0.01108 x 13.00335 amu) + (1 x 10-6 x 14.00317 amu) = 12.011 amu 5 5.1: Atomic and Molecular Mass You can calculate the mass of any compound from the sum of the atomic masses from the periodic table.
    [Show full text]
  • Make an Atom Vocabulary Grade Levels
    MAKE AN ATOM Fundamental to physical science is a basic understanding of the atom. Atoms are comprised of protons, neutrons, and electrons. Protons and neutrons are at the center of the atom while electrons live in lobe-shaped clouds outside the nucleus. The number of electrons usually matches the number of protons, yielding a net neutral charge for the atom. Sometimes an atom has less neutrons or more neutrons than protons. This is called an isotope. If an atom has different numbers of electrons than protons, then it is an ion. If an atom has different numbers of protons, it is a different element all together. Scientists at Idaho National Laboratory study, create, and use radioactive isotopes like Uranium 234. The 234 means this isotope has an atomic mass of 234 Atomic Mass Units (AMU). GRADE LEVELS: 3-8 VOCABULARY Atom – The basic unit of a chemical element. Proton – A stable subatomic particle occurring in all atomic nuclei, with a positive electric charge equal in magnitude to that of an electron, but of opposite sign. Neutron – A subatomic particle of about the same mass as a proton but without an electric charge, present in all atomic nuclei except those of ordinary hydrogen. Electron – A stable subatomic particle with a charge of negative electricity, found in all atoms and acting as the primary carrier of electricity in solids. Orbital – Each of the actual or potential patterns of electron density that may be formed on an atom or molecule by one or more electrons. Ion – An atom or molecule with a net electric charge due to the loss or gain of one or more electrons.
    [Show full text]
  • Molar Mass 1 Molar Mass
    Molar mass 1 Molar mass In chemistry, the molar mass is a physical property. It is defined as the mass of a given substance (chemical element or chemical compound) divided by its amount of substance. The base SI unit for molar mass is kg/mol. However, for historical reasons, molar masses are almost always expressed in g/mol. As an example, the molar mass of water is approximately: M(H O) ≈ 18 g⋅mol−1 2 Molar masses of elements The molar mass of atoms of an element is given by the atomic mass of the element multiplied by the molar mass constant, M −3 u = 1×10 kg/mol = 1 g/mol: M(H) = 1.007 97(7) × 1 g/mol = 1.007 97(7) g/mol M(S) = 32.065(5) × 1 g/mol = 32.065(5) g/mol M(Cl) = 35.453(2) × 1 g/mol = 35.453(2) g/mol M(Fe) = 55.845(2) × 1 g/mol = 55.845(2) g/mol. Multiplying by the molar mass constant ensures that the calculation is dimensionally correct: atomic weights are dimensionless quantities (i.e., pure numbers) whereas molar masses have units (in this case, grams/mole). Some elements are usually encountered as molecules, e.g. hydrogen (H 2), sulfur (S 8), chlorine (Cl 2). The molar mass of molecules of these elements is the molar mass of the atoms multiplied by the number of atoms in each molecule: M(H 2) = 2 × 1.007 97(7) × 1 g/mol = 2.015 88(14) g/mol M(S 8) = 8 × 32.065(5) × 1 g/mol = 256.52(4) g/mol M(Cl 2) = 2 × 35.453(2) × 1 g/mol = 70.906(4) g/mol.
    [Show full text]
  • How Atoms Differ A
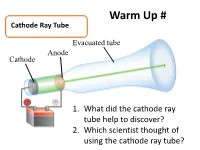
    Warm Up # Cathode Ray Tube Evacuated tube Anode Cathode − + 1. What did the cathode ray tube help to discover? Battery 2. Which scientist thought of using the cathode ray tube? How Atoms Differ a. Properties of Subatomic Particles Particle Symbol Location Relative Relative Actual Charge mass mass (g) outside 1 Electron e- the 9.11 x nucleus -1 1840 10-28 g in the 1.673 x Proton p+ nucleus +1 1 10-24 g in the 1.675 x Neutron 0 n nucleus 0 1 10-24 g Elements on the Periodic Table b. Atomic Number • the number of protons in an atom • Identifies element c. Mass Number •represents the total number of protons and neutrons in the nucleus Mass number A ZX atomic number d. Isotopes • Atoms that have the same number of protons but have a different masses • Ex: 3 isotopes of carbon: 12 13 14 6C 6C 6C e. Average Atomic Mass • the weighted average of the isotopes of that element. • Formula: % mass % Atomic mass abundance of abundance mass of ( ) ( of ) = of x Isotope + of x + … an element Isotope #2 Isotope #1 #1 Isotope #2 Average Atomic Mass • The mass of an atom is so small it is difficult to work with, so chemists have developed an atomic standard to compare all the masses • The standard is the atomic mass unit (amu) • If the mass of an element is not close to a whole number, it is because the atom has several isotopes • The atomic mass is the weighted average of the isotopes of that element Example 1 Silver has two naturally occurring isotopes.
    [Show full text]
  • Isotopes and Atomic Mass
    Name ___________________________ Date ___________________ Class __________________ Chapter 4 • Atomic Structure SMALL-SCALE EXPERIMENT 6 ISOTOPES AND ATOMIC MASS Small-Scale Experiment for text Section 4.3 OBJECTIVES • Determine the average weights of each isotope of the fictitious element vegium. • Determine the relative abundance of isotopes of vegium. • Calculate from experimental data the atomic mass of vegium. INTRODUCTION Isotopes are atoms of the same atomic number having different masses due to different numbers of neutrons. The atomic mass of an element is the weighted average of the masses of the isotopes of that element. The weighted average takes into account both the mass and relative abundance of each isotope as it occurs in nature. The relative abundances and masses of small atomic particles are measured in the laboratory by an instrument called a mass spectrometer. The mass spectrometer separates particles by mass and measures the mass and relative abundance of each. From these data, a weighted average is calculated to determine the atomic mass of the element. PURPOSE In this experiment, you will perform the necessary calculations to determine the atomic mass of the fictitious element vegium. The three different isotopes of vegium are beanium, peaium and cornium. As in real elements, these isotopes are collections of particles having different masses. Your job will be to obtain a sample of vegium and determine the relative abundance of each isotope and the mass of each type of particle. From this data, you will calculate the weighted average mass, or atomic mass, of vegium. Unlike real isotopes, the individual isotopic particles of vegium differ slightly in mass, so you will determine the average mass of each type of isotopic particle.
    [Show full text]
  • The Elements.Pdf
    A Periodic Table of the Elements at Los Alamos National Laboratory Los Alamos National Laboratory's Chemistry Division Presents Periodic Table of the Elements A Resource for Elementary, Middle School, and High School Students Click an element for more information: Group** Period 1 18 IA VIIIA 1A 8A 1 2 13 14 15 16 17 2 1 H IIA IIIA IVA VA VIAVIIA He 1.008 2A 3A 4A 5A 6A 7A 4.003 3 4 5 6 7 8 9 10 2 Li Be B C N O F Ne 6.941 9.012 10.81 12.01 14.01 16.00 19.00 20.18 11 12 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 3 Na Mg IIIB IVB VB VIB VIIB ------- VIII IB IIB Al Si P S Cl Ar 22.99 24.31 3B 4B 5B 6B 7B ------- 1B 2B 26.98 28.09 30.97 32.07 35.45 39.95 ------- 8 ------- 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 4 K Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn Ga Ge As Se Br Kr 39.10 40.08 44.96 47.88 50.94 52.00 54.94 55.85 58.47 58.69 63.55 65.39 69.72 72.59 74.92 78.96 79.90 83.80 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 5 Rb Sr Y Zr NbMo Tc Ru Rh PdAgCd In Sn Sb Te I Xe 85.47 87.62 88.91 91.22 92.91 95.94 (98) 101.1 102.9 106.4 107.9 112.4 114.8 118.7 121.8 127.6 126.9 131.3 55 56 57 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 6 Cs Ba La* Hf Ta W Re Os Ir Pt AuHg Tl Pb Bi Po At Rn 132.9 137.3 138.9 178.5 180.9 183.9 186.2 190.2 190.2 195.1 197.0 200.5 204.4 207.2 209.0 (210) (210) (222) 87 88 89 104 105 106 107 108 109 110 111 112 114 116 118 7 Fr Ra Ac~RfDb Sg Bh Hs Mt --- --- --- --- --- --- (223) (226) (227) (257) (260) (263) (262) (265) (266) () () () () () () http://pearl1.lanl.gov/periodic/ (1 of 3) [5/17/2001 4:06:20 PM] A Periodic Table of the Elements at Los Alamos National Laboratory 58 59 60 61 62 63 64 65 66 67 68 69 70 71 Lanthanide Series* Ce Pr NdPmSm Eu Gd TbDyHo Er TmYbLu 140.1 140.9 144.2 (147) 150.4 152.0 157.3 158.9 162.5 164.9 167.3 168.9 173.0 175.0 90 91 92 93 94 95 96 97 98 99 100 101 102 103 Actinide Series~ Th Pa U Np Pu AmCmBk Cf Es FmMdNo Lr 232.0 (231) (238) (237) (242) (243) (247) (247) (249) (254) (253) (256) (254) (257) ** Groups are noted by 3 notation conventions.
    [Show full text]
  • Mole & Molar Mass
    Mole & Molar Mass Mole (mol): the amount of material counting 6.02214 × 1023 particles The value of the mole is equal to the number of atoms in exactly 12 grams of pure carbon-12. 12.00 g C-12 = 1 mol C-12 atoms = 6.022 × 1023 atoms The number of particles in 1 mole is called Avogadro’s Number (6.0221421 x 1023). 6.022 ×1023 atoms 1 mol or 1 mol 6.022 ×1023 atoms Converting between Number of Moles and Number of Atoms A silver ring contains 1.1 x 1022 silver Calculate the number of atoms in 2.45 atoms. How many moles of silver are in mol of copper. the ring? Atoms Ag mol Ag mol Cu Atoms 23 1 mol 6.022 ×10 atoms 1.1 ×1022 atoms Ag × 2.45 mol Cu × 6.022 ×1023 atoms 1 mol -2 24 = 1.8 × 10 mol Ag = 1.48 × 10 atoms Cu Molar Mass: the mass of 1 mol of atoms of an element An element’s molar mass in g/mol is numerically equal to the element’s atomic mass in amu. 1 mol C 12.01 g C or 12.01 g C 1 mol C Converting between Mass and Number of Moles Converting between Mass and Number of Atoms Calculate the moles of carbon in 0.0265 g of How many aluminum atoms are in a can pencil lead. weighing 16.2 g? g C mol C g Al mol Al atoms Al 1 mol C 0.0265 g C × 1 mol Al 6.022 ×1023 atoms 12.01 g C 16.2 g Al × × 26.98 g Al 1 mol -3 = 2.21 × 10 mol C = 3.62 × 1023 atoms Al Avogadro’s molar mass number Moles Formula units Gram (atoms, molecules, ions) Practice Problems 1.
    [Show full text]
  • Atomic Weights of the Elements 2011 (IUPAC Technical Report)*
    Pure Appl. Chem., Vol. 85, No. 5, pp. 1047–1078, 2013. http://dx.doi.org/10.1351/PAC-REP-13-03-02 © 2013 IUPAC, Publication date (Web): 29 April 2013 Atomic weights of the elements 2011 (IUPAC Technical Report)* Michael E. Wieser1,‡, Norman Holden2, Tyler B. Coplen3, John K. Böhlke3, Michael Berglund4, Willi A. Brand5, Paul De Bièvre6, Manfred Gröning7, Robert D. Loss8, Juris Meija9, Takafumi Hirata10, Thomas Prohaska11, Ronny Schoenberg12, Glenda O’Connor13, Thomas Walczyk14, Shige Yoneda15, and Xiang-Kun Zhu16 1Department of Physics and Astronomy, University of Calgary, Calgary, Canada; 2Brookhaven National Laboratory, Upton, NY, USA; 3U.S. Geological Survey, Reston, VA, USA; 4Institute for Reference Materials and Measurements, Geel, Belgium; 5Max Planck Institute for Biogeochemistry, Jena, Germany; 6Independent Consultant on MiC, Belgium; 7International Atomic Energy Agency, Seibersdorf, Austria; 8Department of Applied Physics, Curtin University of Technology, Perth, Australia; 9National Research Council of Canada, Ottawa, Canada; 10Kyoto University, Kyoto, Japan; 11Department of Chemistry, University of Natural Resources and Applied Life Sciences, Vienna, Austria; 12Institute for Geosciences, University of Tübingen, Tübingen, Germany; 13New Brunswick Laboratory, Argonne, IL, USA; 14Department of Chemistry (Science) and Department of Biochemistry (Medicine), National University of Singapore (NUS), Singapore; 15National Museum of Nature and Science, Tokyo, Japan; 16Chinese Academy of Geological Sciences, Beijing, China Abstract: The biennial review of atomic-weight determinations and other cognate data has resulted in changes for the standard atomic weights of five elements. The atomic weight of bromine has changed from 79.904(1) to the interval [79.901, 79.907], germanium from 72.63(1) to 72.630(8), indium from 114.818(3) to 114.818(1), magnesium from 24.3050(6) to the interval [24.304, 24.307], and mercury from 200.59(2) to 200.592(3).
    [Show full text]
  • Some Basic Concepts of Chemistry
    1 Some Basic Concepts of Chemistry Mole Concept Gram Atomic, Gram Molecular Weight (M) It is 23 the weight of 1.0 mole (Avogadro’s numbers) of atoms, G One Mole Avogadro’s Number ()N = 6.023 ´ 10 . It A moleculesorionsingramunit. is the number of atoms present in exactly 12 g of ()C12 isotope. MA= amu ´ Avogadronumber = A gram Hence, gram molecular weight (M) is numerically equal to G Atomic Weight (A) Atomic weight is the relative weight of one atom of an element with respect to a standard weight. the atomic weight or (molecular weight) in gram unit because Weight of one atom of an element 1.0moleofamuis1.0g. A = 1 th part by weight of an atom of (C12 ) isotope Empirical and Molecular Formula Empirical 12 formula is the simplest formula of a compound with the molecular G amu (atomic mass unit) Weight elements in the simple whole number ratio, and a formula issameoramultipleoftheempiricalformula. 1 12 1amu = thpartbyweightofanatomof ()C isotope e.g. 12 Molecularformula Empiricalformula 1 -24 = g=1.66 ´ 10 g CH6 6 (benzene) CH NA CHO6 12 6 (glucose) CH2 O Atomicweight(A) ´ amu=Absoluteatomicweight. HO2 2 HO NOTE HSO2 2 8 (persulphuricacid) HSO4 G Atomic weight is a relative weight that indicates the relative heavinessofoneatomofanelementwithrespecttoamuweight. G Laws of Chemical Combination Elements combine G Atomicweighthasnounitbecauseitistheratioofweights. in a fixed mass ratio, irrespective of their supplied mass ratio, G Onemoleofanamu=1.00g. e.g. 1 G If an amu is H + O ¾® HO Change of Scale for Atomic Weight 2 2 2 2 defined differently as (1/x)th part by weight of an atom of 2 g 16 g 18 g (C12 )isotope rather (1/12)th part then the atomic weight (A¢ ) Here, H2 and O2 combinesinafixedmassratioof1:8.
    [Show full text]