Make an Atom Vocabulary Grade Levels
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Neutron Stars
Chandra X-Ray Observatory X-Ray Astronomy Field Guide Neutron Stars Ordinary matter, or the stuff we and everything around us is made of, consists largely of empty space. Even a rock is mostly empty space. This is because matter is made of atoms. An atom is a cloud of electrons orbiting around a nucleus composed of protons and neutrons. The nucleus contains more than 99.9 percent of the mass of an atom, yet it has a diameter of only 1/100,000 that of the electron cloud. The electrons themselves take up little space, but the pattern of their orbit defines the size of the atom, which is therefore 99.9999999999999% Chandra Image of Vela Pulsar open space! (NASA/PSU/G.Pavlov et al. What we perceive as painfully solid when we bump against a rock is really a hurly-burly of electrons moving through empty space so fast that we can't see—or feel—the emptiness. What would matter look like if it weren't empty, if we could crush the electron cloud down to the size of the nucleus? Suppose we could generate a force strong enough to crush all the emptiness out of a rock roughly the size of a football stadium. The rock would be squeezed down to the size of a grain of sand and would still weigh 4 million tons! Such extreme forces occur in nature when the central part of a massive star collapses to form a neutron star. The atoms are crushed completely, and the electrons are jammed inside the protons to form a star composed almost entirely of neutrons. -

The Five Common Particles
The Five Common Particles The world around you consists of only three particles: protons, neutrons, and electrons. Protons and neutrons form the nuclei of atoms, and electrons glue everything together and create chemicals and materials. Along with the photon and the neutrino, these particles are essentially the only ones that exist in our solar system, because all the other subatomic particles have half-lives of typically 10-9 second or less, and vanish almost the instant they are created by nuclear reactions in the Sun, etc. Particles interact via the four fundamental forces of nature. Some basic properties of these forces are summarized below. (Other aspects of the fundamental forces are also discussed in the Summary of Particle Physics document on this web site.) Force Range Common Particles It Affects Conserved Quantity gravity infinite neutron, proton, electron, neutrino, photon mass-energy electromagnetic infinite proton, electron, photon charge -14 strong nuclear force ≈ 10 m neutron, proton baryon number -15 weak nuclear force ≈ 10 m neutron, proton, electron, neutrino lepton number Every particle in nature has specific values of all four of the conserved quantities associated with each force. The values for the five common particles are: Particle Rest Mass1 Charge2 Baryon # Lepton # proton 938.3 MeV/c2 +1 e +1 0 neutron 939.6 MeV/c2 0 +1 0 electron 0.511 MeV/c2 -1 e 0 +1 neutrino ≈ 1 eV/c2 0 0 +1 photon 0 eV/c2 0 0 0 1) MeV = mega-electron-volt = 106 eV. It is customary in particle physics to measure the mass of a particle in terms of how much energy it would represent if it were converted via E = mc2. -

Fundamentals of Particle Physics
Fundamentals of Par0cle Physics Particle Physics Masterclass Emmanuel Olaiya 1 The Universe u The universe is 15 billion years old u Around 150 billion galaxies (150,000,000,000) u Each galaxy has around 300 billion stars (300,000,000,000) u 150 billion x 300 billion stars (that is a lot of stars!) u That is a huge amount of material u That is an unimaginable amount of particles u How do we even begin to understand all of matter? 2 How many elementary particles does it take to describe the matter around us? 3 We can describe the material around us using just 3 particles . 3 Matter Particles +2/3 U Point like elementary particles that protons and neutrons are made from. Quarks Hence we can construct all nuclei using these two particles -1/3 d -1 Electrons orbit the nuclei and are help to e form molecules. These are also point like elementary particles Leptons We can build the world around us with these 3 particles. But how do they interact. To understand their interactions we have to introduce forces! Force carriers g1 g2 g3 g4 g5 g6 g7 g8 The gluon, of which there are 8 is the force carrier for nuclear forces Consider 2 forces: nuclear forces, and electromagnetism The photon, ie light is the force carrier when experiencing forces such and electricity and magnetism γ SOME FAMILAR THE ATOM PARTICLES ≈10-10m electron (-) 0.511 MeV A Fundamental (“pointlike”) Particle THE NUCLEUS proton (+) 938.3 MeV neutron (0) 939.6 MeV E=mc2. Einstein’s equation tells us mass and energy are equivalent Wave/Particle Duality (Quantum Mechanics) Einstein E -

An Introduction to Isotopic Calculations John M
An Introduction to Isotopic Calculations John M. Hayes ([email protected]) Woods Hole Oceanographic Institution, Woods Hole, MA 02543, USA, 30 September 2004 Abstract. These notes provide an introduction to: termed isotope effects. As a result of such effects, the • Methods for the expression of isotopic abundances, natural abundances of the stable isotopes of practically • Isotopic mass balances, and all elements involved in low-temperature geochemical • Isotope effects and their consequences in open and (< 200°C) and biological processes are not precisely con- closed systems. stant. Taking carbon as an example, the range of interest is roughly 0.00998 ≤ 13F ≤ 0.01121. Within that range, Notation. Absolute abundances of isotopes are com- differences as small as 0.00001 can provide information monly reported in terms of atom percent. For example, about the source of the carbon and about processes in 13 13 12 13 atom percent C = [ C/( C + C)]100 (1) which the carbon has participated. A closely related term is the fractional abundance The delta notation. Because the interesting isotopic 13 13 fractional abundance of C ≡ F differences between natural samples usually occur at and 13F = 13C/(12C + 13C) (2) beyond the third significant figure of the isotope ratio, it has become conventional to express isotopic abundances These variables deserve attention because they provide using a differential notation. To provide a concrete the only basis for perfectly accurate mass balances. example, it is far easier to say – and to remember – that Isotope ratios are also measures of the absolute abun- the isotope ratios of samples A and B differ by one part dance of isotopes; they are usually arranged so that the per thousand than to say that sample A has 0.3663 %15N more abundant isotope appears in the denominator and sample B has 0.3659 %15N. -

Mass Spectrometry: Quadrupole Mass Filter
Advanced Lab, Jan. 2008 Mass Spectrometry: Quadrupole Mass Filter The mass spectrometer is essentially an instrument which can be used to measure the mass, or more correctly the mass/charge ratio, of ionized atoms or other electrically charged particles. Mass spectrometers are now used in physics, geology, chemistry, biology and medicine to determine compositions, to measure isotopic ratios, for detecting leaks in vacuum systems, and in homeland security. Mass Spectrometer Designs The first mass spectrographs were invented almost 100 years ago, by A.J. Dempster, F.W. Aston and others, and have therefore been in continuous development over a very long period. However the principle of using electric and magnetic fields to accelerate and establish the trajectories of ions inside the spectrometer according to their mass/charge ratio is common to all the different designs. The following description of Dempster’s original mass spectrograph is a simple illustration of these physical principles: The magnetic sector spectrograph PUMP F DD S S3 1 r S2 Fig. 1: Dempster’s Mass Spectrograph (1918). Atoms/molecules are first ionized by electrons emitted from the hot filament (F) and then accelerated towards the entrance slit (S1). The ions then follow a semicircular trajectory established by the Lorentz force in a uniform magnetic field. The radius of the trajectory, r, is defined by three slits (S1, S2, and S3). Ions with this selected trajectory are then detected by the detector D. How the magnetic sector mass spectrograph works: Equating the Lorentz force with the centripetal force gives: qvB = mv2/r (1) where q is the charge on the ion (usually +e), B the magnetic field, m is the mass of the ion and r the radius of the ion trajectory. -

Photons from 252Cf and 241Am-Be Neutron Sources H
Neutronenbestrahlungsraum Calibration Laboratory LB6411 Am-Be Quelle [email protected] Photons from 252Cf and 241Am-Be neutron sources H. Hoedlmoser, M. Boschung, K. Meier and S. Mayer Paul Scherrer Institut, CH-5232 Villigen PSI, Switzerland At the accredited PSI calibration laboratory neutron reference fields traceable to the standards of the Physikalisch-Technische Bundesanstalt (PTB) in Germany are available for the calibration of ambient and personal dose equivalent (rate) meters and passive dosimeters. The photon contribution to H*(10) in the neutron fields of the 252Cf and 241Am-Be sources was measured using various photon dose rate meters and active and passive dosimeters. Measuring photons from a neutron source involves considerable uncertainties due to the presence of neutrons, due to a non-zero neutron sensitivity of the photon detector and due to the energy response of the photon detectors. Therefore eight independent detectors and methods were used to obtain a reliable estimate for the photon contribution as an average of the individual methods. For the 241Am-Be source a photon contribution of approximately 4.9% was determined and for the 252Cf source a contribution of 3.6%. 1) Photon detectors 2) Photons from 252Cf and 241Am-Be neutron sources Figure 1 252Cf decays through -emission (~97%) and through spontaneous fission (~3%) with a half-life of 2.65 y. Both processes are accompanied by photon radiation. Furthermore the spectrum of fission products contains radioactive elements that produce additional gamma photons. In the 241Am-Be source 241Am decays through -emission and various low energy emissions: 241Am237Np + + with a half life of 432.6 y. -
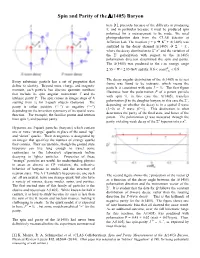
Spin and Parity of the Λ(1405) Baryon
Spin and Parity of the (1405) Baryon here [1], precisely because of the difficulty in producing it, and in particular because it must be produced spin polarized for a measurement to be made. We used photoproduction data from the CLAS detector at Jefferson Lab. The reaction + p K+ + (1405) was analyzed in the decay channel (1405) + + , where the decay distribution to + and the variation of the + polarization with respect to the (1405) polarization direction determined the spin and parity. The (1405) was produced in the c.m. energy range K 2.55 < W < 2.85 GeV and for 0.6 coscm.. 0.9 . The decay angular distribution of the (1405) in its rest Every subatomic particle has a set of properties that frame was found to be isotropic, which means the define its identity. Beyond mass, charge, and magnetic particle is consistent with spin J = ½. The first figure moment, each particle has discrete quantum numbers illustrates how the polarization P of a parent particle that include its spin angular momentum J and its with spin ½, in this case the (1405), transfers intrinsic parity P. The spin comes in integer steps of + starting from ½ for 3-quark objects (baryons). The polarization Q to the daughter baryon, in this case the , depending on whether the decay is in a spatial S wave parity is either positive (“+”) or negative (“”) (L=0) or P wave (L=1). This distinction is what depending on the inversion symmetry of its spatial wave determines the parity of the final state, and hence of the function. For example, the familiar proton and neutron parent. -

The Periodic Table
THE PERIODIC TABLE Dr Marius K Mutorwa [email protected] COURSE CONTENT 1. History of the atom 2. Sub-atomic Particles protons, electrons and neutrons 3. Atomic number and Mass number 4. Isotopes and Ions 5. Periodic Table Groups and Periods 6. Properties of metals and non-metals 7. Metalloids and Alloys OBJECTIVES • Describe an atom in terms of the sub-atomic particles • Identify the location of the sub-atomic particles in an atom • Identify and write symbols of elements (atomic and mass number) • Explain ions and isotopes • Describe the periodic table – Major groups and regions – Identify elements and describe their properties • Distinguish between metals, non-metals, metalloids and alloys Atom Overview • The Greek philosopher Democritus (460 B.C. – 370 B.C.) was among the first to suggest the existence of atoms (from the Greek word “atomos”) – He believed that atoms were indivisible and indestructible – His ideas did agree with later scientific theory, but did not explain chemical behavior, and was not based on the scientific method – but just philosophy John Dalton(1766-1844) In 1803, he proposed : 1. All matter is composed of atoms. 2. Atoms cannot be created or destroyed. 3. All the atoms of an element are identical. 4. The atoms of different elements are different. 5. When chemical reactions take place, atoms of different elements join together to form compounds. J.J.Thomson (1856-1940) 1. Proposed the first model of the atom. 2. 1897- Thomson discovered the electron (negatively- charged) – cathode rays 3. Thomson suggested that an atom is a positively- charged sphere with electrons embedded in it. -

A Discussion on Characteristics of the Quantum Vacuum
A Discussion on Characteristics of the Quantum Vacuum Harold \Sonny" White∗ NASA/Johnson Space Center, 2101 NASA Pkwy M/C EP411, Houston, TX (Dated: September 17, 2015) This paper will begin by considering the quantum vacuum at the cosmological scale to show that the gravitational coupling constant may be viewed as an emergent phenomenon, or rather a long wavelength consequence of the quantum vacuum. This cosmological viewpoint will be reconsidered on a microscopic scale in the presence of concentrations of \ordinary" matter to determine the impact on the energy state of the quantum vacuum. The derived relationship will be used to predict a radius of the hydrogen atom which will be compared to the Bohr radius for validation. The ramifications of this equation will be explored in the context of the predicted electron mass, the electrostatic force, and the energy density of the electric field around the hydrogen nucleus. It will finally be shown that this perturbed energy state of the quan- tum vacuum can be successfully modeled as a virtual electron-positron plasma, or the Dirac vacuum. PACS numbers: 95.30.Sf, 04.60.Bc, 95.30.Qd, 95.30.Cq, 95.36.+x I. BACKGROUND ON STANDARD MODEL OF COSMOLOGY Prior to developing the central theme of the paper, it will be useful to present the reader with an executive summary of the characteristics and mathematical relationships central to what is now commonly referred to as the standard model of Big Bang cosmology, the Friedmann-Lema^ıtre-Robertson-Walker metric. The Friedmann equations are analytic solutions of the Einstein field equations using the FLRW metric, and Equation(s) (1) show some commonly used forms that include the cosmological constant[1], Λ. -

The Subatomic Particle Mass Spectrum
The Subatomic Particle Mass Spectrum Robert L. Oldershaw 12 Emily Lane Amherst, MA 01002 USA [email protected] Key Words: Subatomic Particles; Particle Mass Spectrum; General Relativity; Kerr Metric; Discrete Self-Similarity; Discrete Scale Relativity 1 Abstract: Representative members of the subatomic particle mass spectrum in the 100 MeV to 7,000 MeV range are retrodicted to a first approximation using the Kerr solution of General Relativity. The particle masses appear to form a restricted set of quantized values of a Kerr- based angular momentum-mass relation: M = n1/2 M, where values of n are a set of discrete integers and M is a revised Planck mass. A fractal paradigm manifesting global discrete self- similarity is critical to a proper determination of M, which differs from the conventional Planck mass by a factor of roughly 1019. This exceedingly simple and generic mass equation retrodicts the masses of a representative set of 27 well-known particles with an average relative error of 1.6%. A more rigorous mass formula, which includes the total spin angular momentum rule of Quantum Mechanics, the canonical spin values of the particles, and the dimensionless rotational parameter of the Kerr angular momentum-mass relation, is able to retrodict the masses of the 8 dominant baryons in the 900 MeV to 1700 MeV range at the < 99.7% > level. 2 “There remains one especially unsatisfactory feature [of the Standard Model of particle physics]: the observed masses of the particles, m. There is no theory that adequately explains these numbers. We use the numbers in all our theories, but we do not understand them – what they are, or where they come from. -

Good Practice Guide for Isotope Ratio Mass Spectrometry, FIRMS (2011)
Good Practice Guide for Isotope Ratio Mass Spectrometry Good Practice Guide for Isotope Ratio Mass Spectrometry First Edition 2011 Editors Dr Jim Carter, UK Vicki Barwick, UK Contributors Dr Jim Carter, UK Dr Claire Lock, UK Acknowledgements Prof Wolfram Meier-Augenstein, UK This Guide has been produced by Dr Helen Kemp, UK members of the Steering Group of the Forensic Isotope Ratio Mass Dr Sabine Schneiders, Germany Spectrometry (FIRMS) Network. Dr Libby Stern, USA Acknowledgement of an individual does not indicate their agreement with Dr Gerard van der Peijl, Netherlands this Guide in its entirety. Production of this Guide was funded in part by the UK National Measurement System. This publication should be cited as: First edition 2011 J. F. Carter and V. J. Barwick (Eds), Good practice guide for isotope ratio mass spectrometry, FIRMS (2011). ISBN 978-0-948926-31-0 ISBN 978-0-948926-31-0 Copyright © 2011 Copyright of this document is vested in the members of the FIRMS Network. IRMS Guide 1st Ed. 2011 Preface A few decades ago, mass spectrometry (by which I mean organic MS) was considered a “black art”. Its complex and highly expensive instruments were maintained and operated by a few dedicated technicians and its output understood by only a few academics. Despite, or because, of this the data produced were amongst the “gold standard” of analytical science. In recent years a revolution occurred and MS became an affordable, easy to use and routine technique in many laboratories. Although many (rightly) applaud this popularisation, as a consequence the “black art” has been replaced by a “black box”: SAMPLES GO IN → → RESULTS COME OUT The user often has little comprehension of what goes on “under the hood” and, when “things go wrong”, the inexperienced operator can be unaware of why (or even that) the results that come out do not reflect the sample that goes in. -

Lesson 1: the Single Electron Atom: Hydrogen
Lesson 1: The Single Electron Atom: Hydrogen Irene K. Metz, Joseph W. Bennett, and Sara E. Mason (Dated: July 24, 2018) Learning Objectives: 1. Utilize quantum numbers and atomic radii information to create input files and run a single-electron calculation. 2. Learn how to read the log and report files to obtain atomic orbital information. 3. Plot the all-electron wavefunction to determine where the electron is likely to be posi- tioned relative to the nucleus. Before doing this exercise, be sure to read through the Ins and Outs of Operation document. So, what do we need to build an atom? Protons, neutrons, and electrons of course! But the mass of a proton is 1800 times greater than that of an electron. Therefore, based on de Broglie’s wave equation, the wavelength of an electron is larger when compared to that of a proton. In other words, the wave-like properties of an electron are important whereas we think of protons and neutrons as particle-like. The separation of the electron from the nucleus is called the Born-Oppenheimer approximation. So now we need the wave-like description of the Hydrogen electron. Hydrogen is the simplest atom on the periodic table and the most abundant element in the universe, and therefore the perfect starting point for atomic orbitals and energies. The compu- tational tool we are going to use is called OPIUM (silly name, right?). Before we get started, we should know what’s needed to create an input file, which OPIUM calls a parameter files. Each parameter file consist of a sequence of ”keyblocks”, containing sets of related parameters.