DOCSLIB.ORG

O-C. Atic Correction,Resulting from the Effect of Causes Not Allowed for In

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
O-C. Atic Correction,Resulting from the Effect of Causes Not Allowed for In VOL. 16, 1930 STA TISTICS: W. J. L UYTEN 257 ON SOME STATISTICAL PROPERTIES OF DOUBLE STARS IN SPACE. H1. ON THE MEAN PERIOD OF DOUBLE STARS IN SPA CE By WILLBM J. LUYTSN HARVARD COLLAGS OBS1RVATORY, CAMBRIDGE, MASSACHUSETTS Communicated February 15, 1930 In the previous paper a formula was derived for the computation of the period of a binary star when only the parallax, and the angular separation at a given moment are known. Before actually using such a formula, it is always well to test it on a group of stars for which the period, to be estimated from the formula, is already known with reasonable accuracy. For the data required in this computation, the writer is under obligation to Dr. W. H. Van den Bos who kindly supplied the results of the latest known measures of these double stars-in many cases his own unpublished measures. Table 1 contains the data needed for the actual comparison for 15 binary stars of known parallax and period, arranged in order of increasing period, and designated by the name under which these stars are known to double-star observers. The second, third, and fourth columns con- tain the angular separation, according to the latest known measure, the adopted parallax, and the mass of the system. The fifth column gives the logarithm of the period, calculated by means of the formula derived in the previous paper, which formula is again repeated at the foot of table 1. The sixth and seventh columns show the period derived by double star calculators, and its logarithm, while the eighth column gives the differences O-C. According to formula (1) the standard deviation to be expected in any individual logarithm of period is 0.34 (as a minimum), hence that in the mean of 15 periods should be 0.09. From table 1 we notice that the mean value of log P as calculated from the formula is. 1.83 i 0.09, while that of the observed periods is 1.89. The difference O-C = +0.06, only two-thirds of the standard deviation, is small enough to inspire confidence in formula (1). It may well be explained by accidental errors; yet the possibility should not be excluded that formula (1) requires a small system- atic correction, resulting from the effect of causes not allowed for in its derivation, such as observational selection and discovery chance. The influence of the latter, however, would be expected to act in the opposite sense. From the internal discordances of the values of O-C in the last column, a standard deviation of 0.27 would be indicated for an individual estimate made by means of the formula. Since this value is smaller than Downloaded by guest on October 1, 2021 258 STA TISTICS: W. J. L UYTEN PROC. N. A. S. that derived from the theory, it again inspires confidence in the formula, and we may assume that its present small size is accidental. Formula (1) may now be judged to be reasonably reliable, and we may thus proceed with its application to the problem of the estimation of the mean period of double stars in space. For the definitions used in judging what is a double star, and what is, or are the periods in a multiple system, reference must be made to the previous paper. It appears to the writer TABLE 1 ST" d M ss wGP P(O) woP(O) O-C j 733 0!72 0!100 1.0 1.43 26.7 1.43 0.00 r Her (22084) 1.2 0.112 2.1 1.51 34.5 1.54 +0.03 a CMi 3k 0.307 1.6 1.54 40.2 1.60 +0.06 Mlb 4 AB 1.26 0.140 1.1 1.40 42.2 1.62 +0.22 LHer BC 0.74 0.107 0.90 1.43 43.0 1.63 +0.20 Krii60 AB 1.36 0.258 0.45 1.06 44.3 1.65 +0.59 a CMa AB 10.6 0.366 3.4 2.07 50.0 1.70 -0.37 t UMa AB-CD 1.61 0.145 1.4 1.63 59.9 1.78 +0.15 a Cen AB 7.02 0.757 2.04 1.44 80.1 1.90 +0.46 70 Oph (2 2272) 6.56 0.194 1.7 2.32 87.7 1.94 -0.38 Brsb 13 3.60 0.140 0.8 2.32 130?* 2.11 -0.21 t Boo 3.01 0.173 1.0 2.01 151 2.18 +0.17 A5 (p Uri) 9.22 0.165 2.32 2.58 219 2.34 -0.22 o EriBC 4.52 0.200 0.64 2.27 248 2.39 +0.12 v Cas 8.14 0.180 1.4 2.56 508 2.71 +0.15 1.83 1.89 +0.06 ^0.09 *0.07 * According to the orbit derived by Van den Bos (B. A. N., 2, 29, and 3, 154) the period of Brsb 13 = 41G Arae is 100.9 years. From his own recent measures, however, Dr. Van den Bos concludes that this period is much too short, and estimates the real period at something like 130 years. Log P = 1.460 log d -0.487 log M +0.168 * 0.34 (1) that the solution of the problem may best be attempted by calculating the periods of all double stars nearer than a given distance-ten parsecs in the present investigation. The material has been taken from the list of stars in Harvard Annals, Vol. 85, No. 5. To these have been added a Trianguli, since the re-determination of its parallax at the McCormick Observatory now leaves little doubt about its being nearer than ten par- secs. Among southern stars, the new Yale parallax of p Eridani places this binary well within our limits, while, for the sake of completeness, t Reticuli has also been included, although the parallax of this star is known with but scant measure of certainty. It is possible that another system of parallaxes than the one used here would place 02547, 2 1280, Brsb 5 and ,B 733 = 85 Pegasi further away than 10 parsecs; while it is almost certain that 02;539 AC, and Chri 2448 will fall outside those Downloaded by guest on October 1, 2021 VoL. 16, 1930 STA TISTICS: W. J. L UYTEN 259 limits. In an investigation such as the present, the inclusion of these stars does no harm, provided that no other double star has been omitted nearer than the furthest of those in the present list. This is believed and hoped to be the case, insofar as contemporary parallax information TABLE 2 STAR PRIUOD LOG P a Tri 0.0272 -1.57 t UMa CD 0.027 * -1.56 x Dra 0.769 -0.11 v Boo 1.36 +0.13 t UMa AB 1.82 +0.26 TABLE 3 NAME d T d(A. U.) ABS. MAG. MASS LOG P 02 547 AB 4V8 0!100 .48 9.3, 9.4 0.77 2.68 O2 547 AB-C 330 0.100 3300 9.3, 9.4, 10.2 1.11 5.28 Bo 187 39 0.281 139 10.4, 13.0 0.51 3.44 Millb. 377 2.3 0.115 20 10. 13. 0.51 2.31 K Tuc AB (h 3423) 5.1 0.11? 46 = 5.2, 7.4 1.50 2.51 Lac 353 CD* (I 27) 1.2 0.11? 11- 7.8, 8.8 1.03 1.58 K Tuc-Lac 353 AB-CD 319.4 0.11? 2875 * 5.2, 7.4, 7.8, 8.8 2.53 5.02 Lpz II 961 150 0.142 1060 6.6, 12.2 0.91 4.60 r Ret 310 0.1? 3100 ' 5.2, 5.5 1.8 5.13 o2 Eri A-BCt 83 0.200 415 6.0 + mass 0.64 1.38 3.92 -y Lep (HV 50) 95 0.149 639 4.7, 7.3 1.58 4.17 Z 1280 5.2 0.100 52 8.7, 9.1 0.86 2.70 2 1321 19.4 0.163 119 9.1, 9.1 0.84 3.24 Hu 1128 5.0 0.104 48 5.6, 14 0.99 2.62 Q2 539 AC 7.8 0.095 87 7.3, 9.7 0.95 3.01 Brs 5 (P = 342y??) 1.57 0.100 15.7 8.0, 8.0 1.00 1.91 a Cen AB-Ctt 6740 0.760 8860 15.5 + mass 2.04 2.20 5.77 Sh 190 14.2 0.181 78.8 7.1, 10.2 0.94 2.95 Chri 2448 63.7 0.095 670 8.8 10.5 0.76 4.35 W-Ott 5811 512 0.160 3210 10.2, 12.4 0.56 5.41 Sh 243 AB 4.3 0.174 24.8 6.5, 6.5 1.36 2.14 36 Oph-30 Sco AB-C 730 0.174 4200 6.5, 6.5, 7.8 1.89 5.32 Mlb 4 AB-C 31 0.144 215 11.1 + mass 1.1 1.40 3.51 IA Her A-BC 32 0.105 305 3.7 + mass 0.9 2.20 3.64 Z 2398 16 0.294 54.4 11.1, 11.7 0.55 2.83 h 5173 9 0.243 37 7.2, 13.2 0.78 2.51 61 Cyg (Z 2758) 21 0.300 70 8.0, 8.7 0.95 2.87 * The period of 1 27 may well be 100 years.
Load more

Recommended publications
  • Ioptron AZ Mount Pro Altazimuth Mount Instruction
    ® iOptron® AZ Mount ProTM Altazimuth Mount Instruction Manual Product #8900, #8903 and #8920 This product is a precision instrument. Please read the included QSG before assembling the mount. Please read the entire Instruction Manual before operating the mount. If you have any questions please contact us at [email protected] WARNING! NEVER USE A TELESCOPE TO LOOK AT THE SUN WITHOUT A PROPER FILTER! Looking at or near the Sun will cause instant and irreversible damage to your eye. Children should always have adult supervision while observing. 2 Table of Content Table of Content ......................................................................................................................................... 3 1. AZ Mount ProTM Altazimuth Mount Overview...................................................................................... 5 2. AZ Mount ProTM Mount Assembly ........................................................................................................ 6 2.1. Parts List .......................................................................................................................................... 6 2.2. Identification of Parts ....................................................................................................................... 7 2.3. Go2Nova® 8407 Hand Controller .................................................................................................... 8 2.3.1. Key Description .......................................................................................................................
    [Show full text]
  • Curriculum Vitae
    Neil T. Zimmerman Postdoctoral Research Associate Jan 2014 { Present High Contrast Imaging Laboratory Dept. of Mechanical and Aerospace Engineering Princeton University Princeton, NJ [email protected] http://neilzim.net Professional Experience Postdoctoral Fellow Oct 2011 { Dec 2013 Max Planck Institute for Astronomy Heidelberg, Germany Education Ph.D., Astronomy Oct 2011 Columbia University New York, NY M.Phil., Astronomy May 2008 Columbia University New York, NY M.E., Electrical Engineering May 2006 The Cooper Union for the Advancement of Science and Art New York, NY B.E., Electrical Engineering, Summa Cum Laude May 2004 The Cooper Union for the Advancement of Science and Art New York, NY Postdoctoral Research • Designed a new coronagraph for WFIRST-AFTA optimized for broadband IFS spectroscopy of gas giants. • Developed a low-order wavefront sensor concept applicable to very high-contrast coronagraphy. • Measured the infrared spectral energy distribution of the directly-imaged Jovian analog GJ 504 b. • Made a data pipeline for LEECH, a thermal infrared exoplanet imaging survey at LBT, and delivered the first sensitivity verifications to the collaboration. • Revised the science case for ESPRI, an astrometric exoplanet survey with the VLT Interferometer. • Calibrated a bimorph deformable mirror for the wavefront sensor testbed of the ESO's GRAVITY instru- ment. Ph.D. Thesis: High-Contrast Observations with an Integral Field Spectrograph • Confirmed the physical association of Alcor's M-dwarf companion through a novel relative astrometry technique. • Designed and implemented the data extraction and calibration software for Project 1640, a coronagraphic integral field spectrograph. • Carried out the first combined aperture mask + integral field spectrograph observation.
    [Show full text]
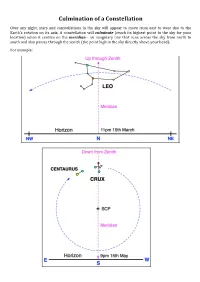
  • Culmination of a Constellation
    Culmination of a Constellation Over any night, stars and constellations in the sky will appear to move from east to west due to the Earth’s rotation on its axis. A constellation will culminate (reach its highest point in the sky for your location) when it centres on the meridian - an imaginary line that runs across the sky from north to south and also passes through the zenith (the point high in the sky directly above your head). For example: When to Observe Constellations The taBle shows the approximate time (AEST) constellations will culminate around the middle (15th day) of each month. Constellations will culminate 2 hours earlier for each successive month. Note: add an hour to the given time when daylight saving time is in effect. The time “12” is midnight. Sunrise/sunset times are rounded off to the nearest half an hour. Sun- Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec Rise 5am 5:30 6am 6am 7am 7am 7am 6:30 6am 5am 4:30 4:30 Set 7pm 6:30 6pm 5:30 5pm 5pm 5pm 5:30 6pm 6pm 6:30 7pm And 5am 3am 1am 11pm 9pm Aqr 5am 3am 1am 11pm 9pm Aql 4am 2am 12 10pm 8pm Ara 4am 2am 12 10pm 8pm Ari 5am 3am 1am 11pm 9pm Aur 10pm 8pm 4am 2am 12 Boo 3am 1am 11pm 9pm 7pm Cnc 1am 11pm 9pm 7pm 3am CVn 3am 1am 11pm 9pm 7pm CMa 11pm 9pm 7pm 3am 1am Cap 5am 3am 1am 11pm 9pm 7pm Car 2am 12 10pm 8pm 6pm Cen 4am 2am 12 10pm 8pm 6pm Cet 4am 2am 12 10pm 8pm Cha 3am 1am 11pm 9pm 7pm Col 10pm 8pm 4am 2am 12 Com 3am 1am 11pm 9pm 7pm CrA 3am 1am 11pm 9pm 7pm CrB 4am 2am 12 10pm 8pm Crv 3am 1am 11pm 9pm 7pm Cru 3am 1am 11pm 9pm 7pm Cyg 5am 3am 1am 11pm 9pm 7pm Del
    [Show full text]
  • Theia: Faint Objects in Motion Or the New Astrometry Frontier
    Theia: Faint objects in motion or the new astrometry frontier The Theia Collaboration ∗ July 6, 2017 Abstract In the context of the ESA M5 (medium mission) call we proposed a new satellite mission, Theia, based on rel- ative astrometry and extreme precision to study the motion of very faint objects in the Universe. Theia is primarily designed to study the local dark matter properties, the existence of Earth-like exoplanets in our nearest star systems and the physics of compact objects. Furthermore, about 15 % of the mission time was dedicated to an open obser- vatory for the wider community to propose complementary science cases. With its unique metrology system and “point and stare” strategy, Theia’s precision would have reached the sub micro-arcsecond level. This is about 1000 times better than ESA/Gaia’s accuracy for the brightest objects and represents a factor 10-30 improvement for the faintest stars (depending on the exact observational program). In the version submitted to ESA, we proposed an optical (350-1000nm) on-axis TMA telescope. Due to ESA Technology readiness level, the camera’s focal plane would have been made of CCD detectors but we anticipated an upgrade with CMOS detectors. Photometric mea- surements would have been performed during slew time and stabilisation phases needed for reaching the required astrometric precision. Authors Management team: Céline Boehm (PI, Durham University - Ogden Centre, UK), Alberto Krone-Martins (co-PI, Universidade de Lisboa - CENTRA/SIM, Portugal) and, in alphabetical order, António Amorim
    [Show full text]
  • Faint Objects in Motion: the New Frontier of High Precision Astrometry
    White paper for the Voyage 2050 long-term plan in the ESA Science Programme Faint objects in motion: the new frontier of high precision astrometry Contact Scientist: Fabien Malbet Institut de Planétologie et d’Astrophysique de Grenoble (IPAG) Université Grenoble Alpes, CS 40700, F-38058 Grenoble cedex 9, France Email: [email protected], Phone: +33 476 63 58 33 version 20190805 Faint objects in motion : the new frontier of high precision astrometry Faint objects in motion: the new on the most critical questions of cosmology, astron- frontier of high precision astrometry omy and particle physics. Sky survey telescopes and powerful targeted telesco- 1.1 Dark matter pes play complementary roles in astronomy. In order to The current hypothesis of cold dark matter (CDM) ur- investigate the nature and characteristics of the mo- gently needs verification. Dark matter (DM) is essential tions of very faint objects, a flexibly-pointed instrument to the L + CDM cosmological model (LCDM), which suc- capable of high astrometric accuracy is an ideal comple- cessfully describes the large-scale distribution of galax- ment to current astrometric surveys and a unique tool for ies and the angular fluctuations of the Cosmic Microwave precision astrophysics. Such a space-based mission Background, as confirmed by the ESA / Planck mission. will push the frontier of precision astrometry from ev- Dark matter is the dominant form of matter (∼ 85%) in idence of earth-massed habitable worlds around the the Universe, and ensures the formation and stability of nearest starts, and also into distant Milky way objects enmeshed galaxies and clusters of galaxies.
    [Show full text]
  • The Detectability of Nightside City Lights on Exoplanets
    Draft version September 6, 2021 Typeset using LATEX twocolumn style in AASTeX63 The Detectability of Nightside City Lights on Exoplanets Thomas G. Beatty1 1Department of Astronomy and Steward Observatory, University of Arizona, Tucson, AZ 85721; [email protected] ABSTRACT Next-generation missions designed to detect biosignatures on exoplanets will also be capable of plac- ing constraints on the presence of technosignatures (evidence for technological life) on these same worlds. Here, I estimate the detectability of nightside city lights on habitable, Earth-like, exoplan- ets around nearby stars using direct-imaging observations from the proposed LUVOIR and HabEx observatories. I use data from the Soumi National Polar-orbiting Partnership satellite to determine the surface flux from city lights at the top of Earth's atmosphere, and the spectra of commercially available high-power lamps to model the spectral energy distribution of the city lights. I consider how the detectability scales with urbanization fraction: from Earth's value of 0.05%, up to the limiting case of an ecumenopolis { or planet-wide city. I then calculate the minimum detectable urbanization fraction using 300 hours of observing time for generic Earth-analogs around stars within 8 pc of the Sun, and for nearby known potentially habitable planets. Though Earth itself would not be detectable by LUVOIR or HabEx, planets around M-dwarfs close to the Sun would show detectable signals from city lights for urbanization levels of 0.4% to 3%, while city lights on planets around nearby Sun-like stars would be detectable at urbanization levels of & 10%. The known planet Proxima b is a particu- larly compelling target for LUVOIR A observations, which would be able to detect city lights twelve times that of Earth in 300 hours, an urbanization level that is expected to occur on Earth around the mid-22nd-century.
    [Show full text]
  • 1903Aj 23 . . . 22K 22 the Asteojsomic Al
    22 THE ASTEOJSOMIC AL JOUENAL. Nos- 531-532 22K . Taking into account the smallness of the weights in- concerned. Through the use of these tables the positions . volved, the individual differences which make up the and motions of many stars not included in the present 23 groups in the preceding table agree^very well. catalogue can be brought into systematic harmony with it, and apparently without materially less accuracy for the in- dividual stars than could be reached by special compu- Tables of Systematic Correction for N2 and A. tations for these stars in conformity with the system of B. 1903AJ The results of the foregoing comparisons. have been This is especially true of the star-places computed by utilized to form tables of systematic corrections for ISr2, An, Dr. Auwers in the catalogues, Ai and As. As will be seen Ai and As. In right-ascension no distinction is necessary by reference to the catalogue the positions and motions of between the various catalogues published by Dr. Auwers, south polar stars taken from N2 agree better with the beginning with the Fundamental-G at alo g ; but in decli- results of this investigation than do those taken from As, nation the distinction between the northern, intermediate, which, in turn, are quoted from the Cape Catalogue for and southern catalogues must be preserved, so far as is 1890. SYSTEMATIC COBEECTIOEB : CEDEE OF DECLINATIONS. Eight-Ascensions ; Cokrections, ¿las and 100z//xtf. Declinations; Corrections, Æs and IOOzZ/x^. B — ISa B —A B —N2 B —An B —Ai âas 100 â[is âas 100 âgô âSs 100
    [Show full text]
  • Ioptron CEM26 Center Balanced Equatorial Mount
    iOptron® CEM26 Center Balanced Equatorial Mount Instruction Manual Product CEM26 and CEM26EC Read the included Quick Setup Guide (QSG) BEFORE taking the mount out of the case! This product is a precision instrument and uses a magnetic gear meshing mechanism. Please read the included QSG before assembling the mount. Please read the entire Instruction Manual before operating the mount. You must hold the mount firmly when disengaging or adjusting the gear switches. Otherwise personal injury and/or equipment damage may occur. Any worm system damage due to improper gear meshing/slippage will not be covered by iOptron’s limited warranty. If you have any questions please contact us at [email protected] WARNING! NEVER USE A TELESCOPE TO LOOK AT THE SUN WITHOUT A PROPER FILTER! Looking at or near the Sun will cause instant and irreversible damage to your eye. Children should always have adult supervision while observing. 2 Table of Content Table of Content ................................................................................................................................................. 3 1. CEM26 Overview ........................................................................................................................................... 5 2. CEM26 Terms ................................................................................................................................................ 6 2.1. Parts List .................................................................................................................................................
    [Show full text]
  • A Green Line Around the Box Means a Habitable Planet Exists in the Starsystem
    Hussey 575 BD+30 2494 BD+24 2733 1.5 BD+14 2774 2.5 1.5 1.5 Ross 512 1.5 WO 9502 1.5 BD+17 2785 2 BD+15 3108 G136-101 Sigma Bootis BD+30 2512 1 Struve 1785 1.5 1 2.5 via LP441.33 1.5 BD+24 2786 1.5 1.5 1.5 1.5 1.5 45 Bootis L1344-37 GJ 3966 Ross 863 1.5 Lambda Serpentis Wolf 497 BD+25 2874 1.5 3 via V645 Herc Gliese 625 1 1.5 3.5 via GJ 3910 3 via V645 Herc 1.5 BD-9 3413 GJ-1179 Zeta Herculis 1.5 Eta Bootes 1 Rho Coronae Borealis 1.5 1.5 2.5 via Giclas 258.33 Luyten 758-105 BD+54 1716 1 BD+25 3173 Giclas 179-43 1.5 1.5 1.5 1 3 via Ross 948 3 via WO 9564 3 via GJ 3796 3 via Ross 948 Eta Coronae Borealis Chi Draconis 3 via HYG86887 1 3.5 via V645 Herc 1 Gamma Serpentis 2 BD+17 2611 (VESTA) Arcturus 3 via V645 Herc 3 via BD+21 2763 3.5 via BD+0 2989, DT Virginis 4 via HYG86887&8 Struve 2135 BD+33 2777 14 Herculis Porimma (Gamma Virginis) 3.5 via BD+45 2247 3 via BD+41 2695 1.5 3.5 BD+60 1623 BD+53 1719 THETIS 1.5 Chi Hercules 2 3.5 1.5 1.5 BD+38 3095 3.5 via BD+46 1189 Mu Herculis 4 via WO 9564 CR Draconis BD+52 2045 3 via BD+43 2796 1.5 3 via Giclas 179-43 BD+36 2393 Queen Isabel Star Sigma Draconis 3.5 via BD+43 2796 CE Bootes 1.5 BD+19 2881 1 1.5 1.5 1.5 2.5 I Bootis via BD+45 2247 BD+47 2112 1 4 via EGWD 329, CR Draconis 3 via LP 272-25 4.5 via Ross 948, L 910-10 44 Bootis Aitkens Double Star 1 ADS 10288 3 via BD+61 2068 1.5 Gilese 625 1.5 Vega 3 via Kuiper 79 3 via Giclas 179-43 4 via BD+46 1189, BD+50 2030 Ross 52 Theta Draconis 2 EV Lacertae Gliese 892 BD+39 2947 3 via BD+18 3421 1.5 0.5 Theta Bootis 1.5 3 via EV Lacertae 2.5 via
    [Show full text]
  • Architecture for Space-Based Exoplanet Spectroscopy in the Mid- Infrared
    Architecture for space-based exoplanet spectroscopy in the mid- infrared Joseph Green*, Case Bradford, Thomas Gautier, Michael Rodgers, Erkin Sidick and Gautam Vasisht Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, CA 91109 ABSTRACT Characterizing exoearths at wavelength about 10 micron offers many benefits over visible coronagraphy. Apart from providing direct access to a number of significant bio-signatures, direct-imaging in the mid-infrared can provides 1000 times or more relaxation to contrast requirements while greatly shortening the time-scales over which the system must be stable. This in-turn enables tremendous relief to optical manufacturing, control and stability tolerances bringing them in- line with current technology state of the art. In this paper, we explore a reference design that co-optimizes a large segmented linearized aperture telescope with one-dimensional phase-induced aperture apodization providing high-contrast imaging for spectroscopic analysis. By rotating about a parent star, the chemical signatures of its planets are characterized while affording additional means for background suppression. Keywords: Exoplanet Spectroscopy, Segmented Space Telescopes, Strip Apertures, PIAA, Mid-Infrared, Coronagraphy 1. INTRODUCTION There have been many concepts over the years pursuing the objective direct imaging and characterization of exoearths in the visible wavelengths. The Terrestrial Planet Finder Coronagraph (TPFC) mission was an earlier examples that found in the baseline
    [Show full text]
  • Instruction Manual
    iOptron® GEM28 German Equatorial Mount Instruction Manual Product GEM28 and GEM28EC Read the included Quick Setup Guide (QSG) BEFORE taking the mount out of the case! This product is a precision instrument and uses a magnetic gear meshing mechanism. Please read the included QSG before assembling the mount. Please read the entire Instruction Manual before operating the mount. You must hold the mount firmly when disengaging or adjusting the gear switches. Otherwise personal injury and/or equipment damage may occur. Any worm system damage due to improper gear meshing/slippage will not be covered by iOptron’s limited warranty. If you have any questions please contact us at [email protected] WARNING! NEVER USE A TELESCOPE TO LOOK AT THE SUN WITHOUT A PROPER FILTER! Looking at or near the Sun will cause instant and irreversible damage to your eye. Children should always have adult supervision while observing. 2 Table of Content Table of Content ................................................................................................................................................. 3 1. GEM28 Overview .......................................................................................................................................... 5 2. GEM28 Terms ................................................................................................................................................ 6 2.1. Parts List .................................................................................................................................................
    [Show full text]
  • Map 5 (Ftnoncanonwork5b.Pdf)
    BD+62°780 3.2 2.7 BD+21°652 GD 294 3.0 BD+53°934 RIM GJ 1073 VERENIGDE 2.2 2.4 SECTOR 1.9 2.7 RANDWAARTS CONCORDIUM 1.9 COMPAGNIE 1.6 5.1 Wolf 230 2.3 BD+20°802 5.1 Lambda Aurigae 2.2 Capella 3.1 BD+52°857 2.7 Iota Persei 3.3 BD+63°238 BD+10°1050 3.6 ADS 5054 IMPERIAL JAPANESE 2.0 2.7 Ranma New New Detroit New New Jersey THE BD+36°1979 STATES 3.4 3.4 BD+74°1047 Wolf 1346 9.4 2.0 4.0 BD+34°363 Theta Persei THOUSAND 3.1 2.3 2.1 3.1 5.2 5.1 NATIONS 4.0 2.9 1.7 2.4 Eta Cephei 3.0 Pivot Dollarton COMMON MIDGARD BD+25°613 3.6 4.1 Thousand Nations BD+09°736 VY Arietis BD+41°328 REPUBLIC 6.4 GJ 1248 0.9 BD+05°1168 5.2 HERDING Gl 895.2 2.8 Iota Pegasi 3.3 BD+24°4357 Alshain 1.5 2.0 Fuji Midori 4.7 5.9 BD+28°1660 1.9 2.5 Iota Ursae Majoris BD+46°1551 GJ 1292 0.7 Alderamin 4.6 4.5 BD+02°305 2.4 GD 806 3.1 BD+04°123 Gl 772 AC+70°8247 1.9 BD+66°1281 2.3 4.4 1.6 5.0 4.3 1.1 4.2 4.4 3.9 1.7 1.9 BD-02°129 Iota Piscium 3.9 Wolf 46 1.8 Mu Cassiopeiae 2.8 8.7 1.9 3.0 Girona 2.7 4.3 3.7 2.5 2.6 2.0 BD-01°565 3.2 LTT 11262 BD+11°383 2.7 3.2 BD+02°4076 3.3 2.1 3.9 New Tokyo 4.1 GJ 1228 3.0 BD+19°279 3.5 BD+20°85 1.6 1.5 Castor 5.1 Kpr 37 3.0 1.7 2.6 3.2 2.1 EURASIAN Theta Ursae Majoris Gl 64 2.3 2.7 4.8 Pi(1) Ursae Majoris SOLAR 2.6 4.0 1.5 2.4 BD-02°0690 5.2 UNION 2.8 2.9 1.6 Delta Aquilae BD+61°1678 2.0 3.9 BD+67°1014 3.4 2.5 BD+56°2966 2.1 FEDERAL 5.3 GJ 1289 3.0 5.9 Vega 2.4 Mu Herculis 2.9 3.4 2.4 New Yamatc 3.4 2.8 STATS 1.8 BD+74°456 2.8 2.2 BS 9088 1.8 BD+28°4704 3.2 4.3 BD+56°1459 BD-05°642 EUROPA 1.7 GJ 1232 2.4 1.5 7.0 Garabaldi Merlon 3.8 1.9 2.8
    [Show full text]