DOCSLIB.ORG

Hypothesis Testing III

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Hypothesis Testing III Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz Hypothesis testing III Botond Szabo Leiden University Leiden, 16 April 2018 Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz Outline 1 Kolmogorov-Smirnov test 2 Mann-Whitney test 3 Normality test 4 Brief summary 5 Quiz Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz One-sample Kolmogorov-Smirnov test IID observations X1;:::; Xn∼ F : Want to test H0 : F = F0 versus H1 : F 6=F0; where F0 is some fixed CDF. Test statistic p p Tn = nDn = n sup jF^n(x) − F0(x)j x If X1;:::; Xn ∼ F0 and F0 is continuous, then the asymptotic distribution of Tn is independent of F0 and is given by the Kolmogorov distribution. Reject the null hypothesis if Tn > Kα; where Kα is the 1 − α quantile of the Kolmogorov distribution. Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz Kolmogorov-Smirnov test (estimated parameters) IID data X1;:::; Xn ∼ F : Want to test H0 : F 2 F versus H1 : F 2= F; where F = fFθ : θ 2 Θg: Test statistic p p ^ Tn = nDn = n sup jFn(x) − Fθ^(x)j; x where θ^ is an estimate of θ based on Xi 's. Astronomers often proceed by treating θ^ as a constant and use the critical values from the usual Kolmogorov-Smirnov test. Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz Kolmogorov-Smirnov test (continued) This is a faulty practice: asymptotically Tn will typically not have the Kolmogorov distribution. Extra work required to obtain the correct critical values. The case when Fθ is the normal CDF has been worked out explicitly (Lilliefors test). Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz Two-sample Kolmogorov-Smirnov test IID observations X1;:::; Xn∼ FX and Y1;:::; Ym∼ FY : Want to test H0 : FX = FY versus H1 : FX 6=FY : Test statistic r nm r nm Tn;m = Dn;m = sup jF^X (x) − F^Y (x)j: n + m n + m x The limit distribution of Tn;m under the null hypothesis is the Kolmogorov distribution. Reject the null hypothesis if Tn;m > Kα; where Kα is the 1 − α quantile of the Kolmogorov distribution. Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz Mann-Whitney test IID observations X1;:::; Xn∼ FX and Y1;:::; Ym∼ FY : Want to test H0 : FX = FY versus H1 : FX 6=FY : Mann-Whitney test (or Wilcoxon rank sum test): Basic idea: group all the n + m observations together, rank them in order of increasing size and look at the rank sum of Y 's, say (Wilcoxon statistic). If the latter takes too unlikelya value compared to what we could have obtained under the null hypthesis, we reject the null hypothesis. Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz Example Example Consider the data in the following table (ranks are shown in parentheses): X 0s Y 's 1 (1) 6 (4) 3 (2) 4 (3) The rank sum of X 's is 3 and that of Y 's is R = 7: 4 Under the null hypothesis each of the 2 = 6 assignments of ranks to Y 's are equally likely. Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz Example (continued) Example Ranks R f1; 2g 3 f1; 3g 4 f1; 4g 5 f2; 3g 5 f2; 4g 6 f3; 4g 7 Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz Example (continued) Example Under the null hypothesis the distribution of R is: r 3 4 5 6 7 1 1 1 1 1 P(R = r) 6 6 3 6 6 In particular, P(R = 7) = 1=6: So if the null hypothesis were true, the rank sum we saw would occur one time out of six purely on the basis of chance. Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz Mann-Whitney test: formalisation It can be shown that the rank sum (Wilcoxon statistic) can be expressed in terms of the Mann-Whitney statistic m n 1 X X U = 1 : mn [Xi <Yj ] i=1 j=1 The latter is an estimator of P(X < Y ): If FX =FY ; then P(X < Y ) = 1=2: The statistic U is trying to detect deviation from this. Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz Shapiro-Wilk test IID observations X1;:::; Xn ∼ F : Want to test H0 : F is normal vs H1 : F is not normal : Test statistic Pn 2 ( ai X ) W = i=1 (i) ; n Pn 2 i=1(Xi − X ) where X(i) is the ith order statistics, mT V −1 (a ;:::; a ) = ; 1 n (mT V −1V −1m)1=2 with mi 's the expectations of order statistics of IID standard normal random variables Z1;:::; Zn; and V is the corresponding covariance matrix. Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz Shapiro-Wilk test (continued) The test rejects for small values of Wn: The distribution of Wn is tabulated (or approximated), which allows determination of the critical values. Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz Brief summary Wald test relies on an asymptotic argument and is useful in the large sample settings. t-test is exact (no asymptotics) and useful, but makes the normality assumption. Likelihood ratio test is excellent, and even the best in various senses in various setups, but makes parametric assumptions. There are many normality tests, Shapiro-Wilk is just one example. They complement nicely graphical tools for checking normality (histogram, QQ-plot). Not so useful with small samples, but small samples always pose difficulties. Nonparametric tests are nice, sometimes exact, other times based on asymptotic arguments. No silver bullet. Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz Question 1 What is not true for the one-sample Kolmogorov-Smirnov test? Answers: 1 It is a nonparametric test. p ^ 2 The test statistics is Tn = n supx jFn(x) − F0(x)j 3 The asymptotic distribution of Tn depends on F0. 4 The asymptotic distribution of Tn is the Kolmogorov distribution. Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz Question 1 What is not true for the one-sample Kolmogorov-Smirnov test? Answers: 1 It is a nonparametric test. p ^ 2 The test statistics is Tn = n supx jFn(x) − F0(x)j 3 The asymptotic distribution of Tn depends on F0. 4 The asymptotic distribution of Tn is the Kolmogorov distribution. Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz Question 2 What is the basic idea in the Mann-Whitney test for checking if two data sets are coming from the same distribution? Answers: 1 Rank the observations and check if the rand sum of the first sample is not too unlikely. 2 Check if the average of the observations is different. 3 The empirical distributions are close to each other. 4 The difference of the observations should concentrate aorund zero. Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz Question 2 What is the basic idea in the Mann-Whitney test for checking if two data sets are coming from the same distribution? Answers: 1 Rank the observations and check if the rand sum of the first sample is not too unlikely. 2 Check if the average of the observations is different. 3 The empirical distributions are close to each other. 4 The difference of the observations should concentrate aorund zero. Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz Question 3 What is not true for the Shapiro-Wilk test? Answers: 1 It is a nonparametric test. 2 It is a normality test. 3 The distribution of the test statisitcs Wn is given in a table. 4 It is the single best test to check normality and especially useful for small sample size. Kolmogorov-Smirnov test Mann-Whitney test Normality test Brief summary Quiz Question 3 What is not true for the Shapiro-Wilk test? Answers: 1 It is a nonparametric test. 2 It is a normality test. 3 The distribution of the test statisitcs Wn is given in a table. 4 It is the single best test to check normality and especially useful for small sample size..
Load more

Recommended publications
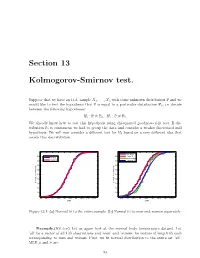
  • Section 13 Kolmogorov-Smirnov Test
    Section 13 Kolmogorov-Smirnov test. Suppose that we have an i.i.d. sample X1; : : : ; Xn with some unknown distribution P and we would like to test the hypothesis that P is equal to a particular distribution P0; i.e. decide between the following hypotheses: H : P = P ; H : P = P : 0 0 1 6 0 We already know how to test this hypothesis using chi-squared goodness-of-fit test. If dis­ tribution P0 is continuous we had to group the data and consider a weaker discretized null hypothesis. We will now consider a different test for H0 based on a very different idea that avoids this discretization. 1 1 men data 0.9 0.9 'men' fit all data women data 0.8 normal fit 0.8 'women' fit 0.7 0.7 0.6 0.6 0.5 0.5 0.4 0.4 Cumulative probability 0.3 Cumulative probability 0.3 0.2 0.2 0.1 0.1 0 0 96 96.5 97 97.5 98 98.5 99 99.5 100 100.5 96.5 97 97.5 98 98.5 99 99.5 100 100.5 Data Data Figure 13.1: (a) Normal fit to the entire sample. (b) Normal fit to men and women separately. Example.(KS test) Let us again look at the normal body temperature dataset. Let ’all’ be a vector of all 130 observations and ’men’ and ’women’ be vectors of length 65 each corresponding to men and women. First, we fit normal distribution to the entire set ’all’.
    [Show full text]
  • Downloaded 09/24/21 09:09 AM UTC
    MARCH 2007 NOTES AND CORRESPONDENCE 1151 NOTES AND CORRESPONDENCE A Cautionary Note on the Use of the Kolmogorov–Smirnov Test for Normality DAG J. STEINSKOG Nansen Environmental and Remote Sensing Center, and Bjerknes Centre for Climate Research, and Geophysical Institute, University of Bergen, Bergen, Norway DAG B. TJØSTHEIM Department of Mathematics, University of Bergen, Bergen, Norway NILS G. KVAMSTØ Geophysical Institute, University of Bergen, and Bjerknes Centre for Climate Research, Bergen, Norway (Manuscript received and in final form 28 April 2006) ABSTRACT The Kolmogorov–Smirnov goodness-of-fit test is used in many applications for testing normality in climate research. This note shows that the test usually leads to systematic and drastic errors. When the mean and the standard deviation are estimated, it is much too conservative in the sense that its p values are strongly biased upward. One may think that this is a small sample problem, but it is not. There is a correction of the Kolmogorov–Smirnov test by Lilliefors, which is in fact sometimes confused with the original Kolmogorov–Smirnov test. Both the Jarque–Bera and the Shapiro–Wilk tests for normality are good alternatives to the Kolmogorov–Smirnov test. A power comparison of eight different tests has been undertaken, favoring the Jarque–Bera and the Shapiro–Wilk tests. The Jarque–Bera and the Kolmogorov– Smirnov tests are also applied to a monthly mean dataset of geopotential height at 500 hPa. The two tests give very different results and illustrate the danger of using the Kolmogorov–Smirnov test. 1. Introduction estimates of skewness and kurtosis. Such moments can be used to diagnose nonlinear processes and to provide The Kolmogorov–Smirnov test (hereafter the KS powerful tools for validating models (see also Ger- test) is a much used goodness-of-fit test.
    [Show full text]
  • Exponentiality Test Using a Modified Lilliefors Test Achut Prasad Adhikari
    University of Northern Colorado Scholarship & Creative Works @ Digital UNC Dissertations Student Research 5-1-2014 Exponentiality Test Using a Modified Lilliefors Test Achut Prasad Adhikari Follow this and additional works at: http://digscholarship.unco.edu/dissertations Recommended Citation Adhikari, Achut Prasad, "Exponentiality Test Using a Modified Lilliefors Test" (2014). Dissertations. Paper 63. This Text is brought to you for free and open access by the Student Research at Scholarship & Creative Works @ Digital UNC. It has been accepted for inclusion in Dissertations by an authorized administrator of Scholarship & Creative Works @ Digital UNC. For more information, please contact [email protected]. UNIVERSITY OF NORTHERN COLORADO Greeley, Colorado The Graduate School AN EXPONENTIALITY TEST USING A MODIFIED LILLIEFORS TEST A Dissertation Submitted in Partial Fulfillment Of the Requirements for the Degree of Doctor of Philosophy Achut Prasad Adhikari College of Education and Behavioral Sciences Department of Applied Statistics and Research Methods May 2014 ABSTRACT Adhikari, Achut Prasad An Exponentiality Test Using a Modified Lilliefors Test. Published Doctor of Philosophy dissertation, University of Northern Colorado, 2014. A new exponentiality test was developed by modifying the Lilliefors test of exponentiality for the purpose of improving the power of the test it directly modified. Lilliefors has considered the maximum absolute differences between the sample empirical distribution function (EDF) and the exponential cumulative distribution function (CDF). The proposed test considered the sum of all the absolute differences between the CDF and EDF. By considering the sum of all the absolute differences rather than only a point difference of each observation, the proposed test would expect to be less affected by individual extreme (too low or too high) observations and capable of detecting smaller, but consistent, differences between the distributions.
    [Show full text]
  • Power Comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling Tests
    Journal ofStatistical Modeling and Analytics Vol.2 No.I, 21-33, 2011 Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests Nornadiah Mohd Razali1 Yap Bee Wah 1 1Faculty ofComputer and Mathematica/ Sciences, Universiti Teknologi MARA, 40450 Shah Alam, Selangor, Malaysia E-mail: nornadiah@tmsk. uitm. edu.my, yapbeewah@salam. uitm. edu.my ABSTRACT The importance of normal distribution is undeniable since it is an underlying assumption of many statistical procedures such as I-tests, linear regression analysis, discriminant analysis and Analysis of Variance (ANOVA). When the normality assumption is violated, interpretation and inferences may not be reliable or valid. The three common procedures in assessing whether a random sample of independent observations of size n come from a population with a normal distribution are: graphical methods (histograms, boxplots, Q-Q-plots), numerical methods (skewness and kurtosis indices) and formal normality tests. This paper* compares the power offour formal tests of normality: Shapiro-Wilk (SW) test, Kolmogorov-Smirnov (KS) test, Lillie/ors (LF) test and Anderson-Darling (AD) test. Power comparisons of these four tests were obtained via Monte Carlo simulation of sample data generated from alternative distributions that follow symmetric and asymmetric distributions. Ten thousand samples ofvarious sample size were generated from each of the given alternative symmetric and asymmetric distributions. The power of each test was then obtained by comparing the test of normality statistics with the respective critical values. Results show that Shapiro-Wilk test is the most powerful normality test, followed by Anderson-Darling test, Lillie/ors test and Kolmogorov-Smirnov test. However, the power ofall four tests is still low for small sample size.
    [Show full text]
  • Univariate Analysis and Normality Test Using SAS, STATA, and SPSS
    © 2002-2006 The Trustees of Indiana University Univariate Analysis and Normality Test: 1 Univariate Analysis and Normality Test Using SAS, STATA, and SPSS Hun Myoung Park This document summarizes graphical and numerical methods for univariate analysis and normality test, and illustrates how to test normality using SAS 9.1, STATA 9.2 SE, and SPSS 14.0. 1. Introduction 2. Graphical Methods 3. Numerical Methods 4. Testing Normality Using SAS 5. Testing Normality Using STATA 6. Testing Normality Using SPSS 7. Conclusion 1. Introduction Descriptive statistics provide important information about variables. Mean, median, and mode measure the central tendency of a variable. Measures of dispersion include variance, standard deviation, range, and interquantile range (IQR). Researchers may draw a histogram, a stem-and-leaf plot, or a box plot to see how a variable is distributed. Statistical methods are based on various underlying assumptions. One common assumption is that a random variable is normally distributed. In many statistical analyses, normality is often conveniently assumed without any empirical evidence or test. But normality is critical in many statistical methods. When this assumption is violated, interpretation and inference may not be reliable or valid. Figure 1. Comparing the Standard Normal and a Bimodal Probability Distributions Standard Normal Distribution Bimodal Distribution .4 .4 .3 .3 .2 .2 .1 .1 0 0 -5 -3 -1 1 3 5 -5 -3 -1 1 3 5 T-test and ANOVA (Analysis of Variance) compare group means, assuming variables follow normal probability distributions. Otherwise, these methods do not make much http://www.indiana.edu/~statmath © 2002-2006 The Trustees of Indiana University Univariate Analysis and Normality Test: 2 sense.
    [Show full text]
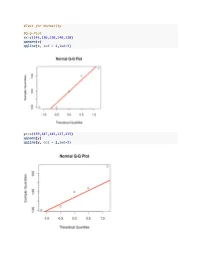
  • Test for Normality #QQ-Plot X<-C(145130120140120
    #Test for Normality #Q-Q-Plot x<-c(145,130,120,140,120) qqnorm(x) qqline(x, col = 2,lwd=3) y<-c(159,147,145,137,135) qqnorm(y) qqline(y, col = 2,lwd=3) #Lilliefors Test #install.packages("nortest") library(nortest) x<-c(145,130,120,140,120) y<-c(159,147,145,137,135) lillie.test(x) ## ## Lilliefors (Kolmogorov-Smirnov) normality test ## ## data: x ## D = 0.23267, p-value = 0.4998 lillie.test(y) ## ## Lilliefors (Kolmogorov-Smirnov) normality test ## ## data: y ## D = 0.20057, p-value = 0.7304 #Mann-Whitney-U Test #MWU Test: unpaired data x<-c(5,5,4,5,3) y<-c(22,14,5,17,30) #exact MWU Test, problem with ties wilcox.test(x,y) ## Warning in wilcox.test.default(x, y): cannot compute exact p-value with ## ties ## ## Wilcoxon rank sum test with continuity correction ## ## data: x and y ## W = 1.5, p-value = 0.02363 ## alternative hypothesis: true location shift is not equal to 0 #asymptotic MWU Test with continuity correction wilcox.test(x,y,exact=FALSE, correct=FALSE) ## ## Wilcoxon rank sum test ## ## data: x and y ## W = 1.5, p-value = 0.01775 ## alternative hypothesis: true location shift is not equal to 0 #asymptotic MWU Test without continuity correction wilcox.test(x,y,exact=FALSE, correct=TRUE) ## ## Wilcoxon rank sum test with continuity correction ## ## data: x and y ## W = 1.5, p-value = 0.02363 ## alternative hypothesis: true location shift is not equal to 0 #Calculating the ranks salve<-c(x,y) group<-c(rep("A",length(x)),rep("B",length(y))) data<-data.frame(salve,group) r1<-sum(rank(data$salve)[data$group=="A"]) r1 ## [1] 16.5 r2<-sum(rank(data$salve)[data$group=="B"])
    [Show full text]
  • Nonparametric Methods
    Chapter 6 Nonparametric Methods CHAPTER VI; SECTION A: INTRODUCTION TO NONPARAMETRIC METHODS Purposes of Nonparametric Methods: Nonparametric methods are uniquely useful for testing nominal (categorical) and ordinal (ordered) scaled data--situations where parametric tests are not generally available. An important second use is when an underlying assumption for a parametric method has been violated. In this case, the interval/ratio scale data can be easily transformed into ordinal scale data and the counterpart nonparametric method can be used. Inferential and Descriptive Statistics: The nonparametric methods described in this chapter are used for both inferential and descriptive statistics. Inferential statistics use data to draw inferences (i.e., derive conclusions) or to make predictions. In this chapter, nonparametric inferential statistical methods are used to draw conclusions about one or more populations from which the data samples have been taken. Descriptive statistics aren’t used to make predictions but to describe the data. This is often best done using graphical methods. Examples: An analyst or engineer might be interested to assess the evidence regarding: 1. The difference between the mean/median accident rates of several marked and unmarked crosswalks (when parametric Student’s t test is invalid because sample distributions are not normal). 2. The differences between the absolute average errors between two types of models for forecasting traffic flow (when analysis of variance is invalid because distribution of errors is not normal). 3. The relationship between the airport site evaluation ordinal rankings of two sets of judges, i.e., citizens and airport professionals. 4. The differences between neighborhood districts in their use of a regional mall for purposes of planning transit routes.
    [Show full text]
  • Null Hypothesis Against an Alternative Hypothesis
    Medical Statistics with R Dr. Gulser Caliskan Prof. Giuseppe Verlato Unit of Epidemiology and Medical Statistics Department of Diagnostics and Public Health University of Verona, Italy LESSON 4 INDEX 1. Independent T-Test 2. Wilcoxon Rank-Sum (Mann-Whitney U Test) 3. Paired T-Test 4. Wilcoxon Sign Test 5. ANOVA (Analysis of Varyans) 6. Kruskal Wallis H Test Classical Hypothesis Testing Test of a null hypothesis against an alternative hypothesis. There are five steps, the first four of which should be done before inspecting the data. Step 1. Declare the null hypothesis H0 and the alternative hypothesis H1. Types Of Hypotheses A hypothesis that completely specifies the parameters is called simple. If it leaves some parameter undetermined it is composite. A hypothesis is one-sided if it proposes that a parameter is > some value or < some value; it is two-sided if it simply says the parameter is /= some value. Types of Error Rejecting H0 when it is actually true is called a Type I Error. In biomedical settings it can be considered a false positive. (Null hypothesis says “nothing is happening” but we decide“there is disease”.) Step 2. Specify an acceptable level of Type I error, α, normally 0.05 or 0.01. This is the threshold used in deciding to reject H0 or not. If α = 0.05 and we determine the probability of our data assuming H0 is 0.0001, then we reject H0. The Test Statistic Step 3. Select a test statistic. This is a quantity calculated from the data whose value leads me to reject the null hypothesis or not.
    [Show full text]
  • Power Comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling Tests
    Journal of Statistical Modeling and Analytics Vol.2 No.1, 21-33, 2011 Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests Nornadiah Mohd Razali1 Yap Bee Wah1 1Faculty of Computer and Mathematical Sciences, Universiti Teknologi MARA, 40450 Shah Alam, Selangor, Malaysia E-mail: [email protected], [email protected] ABSTRACT The importance of normal distribution is undeniable since it is an underlying assumption of many statistical procedures such as t-tests, linear regression analysis, discriminant analysis and Analysis of Variance (ANOVA). When the normality assumption is violated, interpretation and inferences may not be reliable or valid. The three common procedures in assessing whether a random sample of independent observations of size n come from a population with a normal distribution are: graphical methods (histograms, boxplots, Q-Q-plots), numerical methods (skewness and kurtosis indices) and formal normality tests. This paper* compares the power of four formal tests of normality: Shapiro-Wilk (SW) test, Kolmogorov-Smirnov (KS) test, Lilliefors (LF) test and Anderson-Darling (AD) test. Power comparisons of these four tests were obtained via Monte Carlo simulation of sample data generated from alternative distributions that follow symmetric and asymmetric distributions. Ten thousand samples of various sample size were generated from each of the given alternative symmetric and asymmetric distributions. The power of each test was then obtained by comparing the test of normality statistics with the respective critical values. Results show that Shapiro-Wilk test is the most powerful normality test, followed by Anderson-Darling test, Lilliefors test and Kolmogorov-Smirnov test.
    [Show full text]
  • Normality Assumption in Statistical Data Analysis
    Data Science NORMALITY ASSUMPTION IN STATISTICAL DATA ANALYSIS S.Ya. Shatskikh1, L.E. Melkumova2 1Samara National Research University, Samara, Russia 2Mercury Development Russia, Samara, Russia Abstract. The article is devoted to normality assumption in statistical data analysis. It gives a short historical review of the development of scientific views on the normal law and its applications. It also briefly covers normality tests and analyzes possible consequences of using the normality assumption incorrectly. Keywords: normal law, normality assumption, normal distribution, Gaussian distribution, central limit theorem, normality tests. Citation: Shatskikh SYa, Melkumova LE. Normality assumption in statistical data analysis. CEUR Workshop Proceedings, 2016; 1638: 763-768. DOI: 10.18287/1613-0073-2016-1638-763-768 “Mechanism" of the central limit theorem Normal distribution can serve as a good approximation for processing observations if the random variable in question can be considered as a sum of a large number of in- dependent random variables 푋1, … , 푋푛, where each of the variables contributes to the common sum: 1 푥 푛 푛 2 푢2 2 1 − Lim ℙ {∑ (푋푘 − 푚푘)⁄(∑ 휎푘 ) ≤ 푥 } = ∫ 푒 2 푑푢, 푛→∞ √2휋 푘=1 푘=1 −∞ 2 필{푋푘} = 푚푘, 픻{푋푘} = 휎푘 < ∞. This theory was developed in the classical limit theorems, namely the De Moivre- Laplace theorem, the Lyapunov theorem and the Lindeberg-Feller theorem. By the beginning of the 20th century this argument already had a rather wide support in practice. Many practical experiments confirmed that the observed distributions obey the normal law. The general acknowledgement of the normal law at that point of time was mainly based on observations and measurement results in physical sciences and in particular in astronomy and geodesy.
    [Show full text]
  • VILACOMUN-THESIS-2017.Pdf
    Copyright by Alfredo Vila Común 2017 The Thesis Committee for Alfredo Vila Común Certifies that this is the approved version of the following thesis: Exploratory Study of Visual Management Application in Peruvian Construction Projects APPROVED BY SUPERVISING COMMITTEE: Supervisor: Carlos H. Caldas Fernanda Leite Exploratory Study of Visual Management Application in Peruvian Construction Projects by Alfredo Vila Común Thesis Presented to the Faculty of the Graduate School of The University of Texas at Austin in Partial Fulfillment of the Requirements for the Degree of Master of Science in Engineering The University of Texas at Austin December 2017 Dedication This thesis is dedicated to my beloved wife, for her love, patience, and continued encouragement; To my beloved family, for their support. Acknowledgements I would like to thank Dr. Carlos H. Caldas for all his support, guidance, availability, confidence, and wisdom to assist me, without which this thesis would not have been possible. I am extremely grateful to him. I would also like to thank Dr. Fernanda Leite for their advice and encouragement, and to all CEPM faculty for sharing their knowledge with me through classes and informal chats. I would also like to extend my gratitude to PRONABEC, without its scholarship programs this experience abroad would not have been possible for me. Thanks to all survey participants, especially the ones that allowed me to visit their projects, and share their knowledge to enrich this study. Finally, special thanks to Construction Engineering and Project Management students, who provided me with so much advice, friendship, and support, which really made graduate school a much more rewarding experience.
    [Show full text]
  • Modified Lilliefors Test Achut Adhikari University of Northern Colorado, [email protected]
    Journal of Modern Applied Statistical Methods Volume 14 | Issue 1 Article 9 5-1-2015 Modified Lilliefors Test Achut Adhikari University of Northern Colorado, [email protected] Jay Schaffer University of Northern Colorado, [email protected] Follow this and additional works at: http://digitalcommons.wayne.edu/jmasm Recommended Citation Adhikari, Achut and Schaffer, Jay (2015) "Modified Lilliefors Test," Journal of Modern Applied Statistical Methods: Vol. 14 : Iss. 1 , Article 9. DOI: 10.22237/jmasm/1430453280 Available at: http://digitalcommons.wayne.edu/jmasm/vol14/iss1/9 This Regular Article is brought to you for free and open access by the Open Access Journals at DigitalCommons@WayneState. It has been accepted for inclusion in Journal of Modern Applied Statistical Methods by an authorized editor of DigitalCommons@WayneState. Journal of Modern Applied Statistical Methods Copyright © 2015 JMASM, Inc. May 2015, Vol. 14, No. 1, 53-69. ISSN 1538 − 9472 Modified Lilliefors Test A. Adhikari J. Schaffer University of Northern Colorado University of Northern Colorado Greeley, Colorado Greeley, Colorado A new exponentiality test was developed by modifying the Lilliefors test of exponentiality. The proposed test considered the sum of all the absolute differences between the exponential cumulative distribution function (CDF) and the sample empirical distribution function (EDF). The proposed test is simple to understand and easy to compute. Keywords: Cumulative distribution function, empirical distribution function, exponentiality test, critical value, significance level, and power Introduction Exponential distributions are quite often used in duration models and survival analysis, including several applications in macroeconomics, finance and labor economics (optimal insurance policy, duration of unemployment spell, retirement behavior, etc.).
    [Show full text]