DOCSLIB.ORG

AN16-LS16 Abstracts

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
AN16-LS16 Abstracts AN16-LS16 Abstracts Abstracts are printed as submitted by the authors. Society for Industrial and Applied Mathematics 3600 Market Street, 6th Floor Philadelphia, PA 19104-2688 USA Telephone: +1-215-382-9800 Fax: +1-215-386-7999 Conference E-mail: [email protected] Conference web: www.siam.org/meetings/ Membership and Customer Service: 800-447-7426 (US & Canada) or +1-215-382-9800 (worldwide) 2 2016 SIAM Annual Meeting Table of Contents AN16 Annual Meeting Abstracts ................................................4 LS16 Life Sciences Abstracts ...................................................157 SIAM Presents Since 2008, SIAM has recorded many Invited Lectures, Prize Lectures, and selected Minisymposia from various conferences. These are available by visiting SIAM Presents (http://www.siam.org/meetings/presents.php). 2016 SIAM Annual Meeting 3 AN16 Abstracts 4 AN16 Abstracts SP1 University of Cambridge AWM-SIAM Sonia Kovalevsky Lecture - Bioflu- [email protected] ids of Reproduction: Oscillators, Viscoelastic Net- works and Sticky Situations JP1 From fertilization to birth, successful mammalian repro- Spatio-temporal Dynamics of Childhood Infectious duction relies on interactions of elastic structures with a Disease: Predictability and the Impact of Vaccina- fluid environment. Sperm flagella must move through cer- tion vical mucus to the uterus and into the oviduct, where fertil- ization occurs. In fact, some sperm may adhere to oviduc- Violent epidemics of childhood infections such as measles tal epithelia, and must change their pattern of oscillation provide a particularly clear illustration of oscillatory to escape. In addition, coordinated beating of oviductal ’predator-prey’ dynamics. We discuss limits on the pre- cilia also drives the flow. Sperm-egg penetration, trans- dictability of these systems, both in the era before vacci- port of the fertilized ovum from the oviduct to its implan- nation and at present, where vaccine hesitancy limits the tation in the uterus and, indeed, birth itself are rich ex- effectiveness of vaccination programs in many countries. amples of elasto-hydrodynamic coupling. We will discuss We also discuss the impact of viral evolution on predictabil- successes and challenges in the mathematical and compu- ity and the design of vaccination programs, with particular tational modeling of the biofluids of reproduction. In addi- reference to influenza and rotavirus. tion, we will present reduced models that evoke intriguing questions in fundamental fluid dynamics. Bryan Grenfell Princeton University Lisa J. Fauci [email protected] Tulane University Department of Mathematics [email protected] CP1 Analysis of Block Methods for Toeplitz Matrices SP2 Toeplitz matrices and matrices from related matrix alge- The John von Neumann Lecture: Satisfiability and bras arise in a variety of applications including signal pro- Combinatorics cessing and partial differential equations. The analysis of iterative solvers for linear systems is usually based on The Satisfiability Problem, which asks whether or not a studying the generating symbol of the iteration matrix. given Boolean formula can be satisfied for some values of Block methods can be studied using proper decomposi- its variables, has long been thought to be computationally tions of the matrices, resulting in analyses that fit in the hopeless. Indeed, SAT is the well-known ”Poster Child” established framework used to analyze non-blocked meth- for NP-complete problems. But algorithmic breakthroughs ods. These techniques will be presented in this talk. have made it possible for many important special cases of the problem to be solved efficiently. Industrial-strength Matthias Bolten ”SAT solvers” have become a billion-dollar industry, and University of Wuppertal they play a vital part in the design of contemporary com- Department of Mathematics puters. The speaker will explain how the new SAT tech- [email protected] nology also helps us to solve a wide variety of problems that belong to combinatorial mathematics. CP1 Donald E. Knuth A Feast Eigenvalue Algorithm Without Solving Stanford University Linear Systems mam(at)theory.stanford.edu The FEAST Eigenvalue algorithm uses a shift-invert strat- egy that requires solving multiple linear systems in the SP3 complex plane. Similarly to other shift-invert algorithms, W.T. and Idalia Reid Prize in Mathematics solving the linear systems represents the most challenging part of the computation. We present an innovative mod- Not available at time of publication. ification of FEAST that finds interior eigenpairs without solving linear systems, instead using only a few iterations Ioannis Kevrekidis of iterative refinement per subspace update, thus removing Dept. of Chemical Engineering the need for using matrix factorizations or preconditioner Princeton University matrices. [email protected] Brendan Gavin ECE Department SP4 University of Massachusetts, Amherst I. E. Block Community Lecture: Toy Models [email protected] Would you like to come see some toys? ’Toys’ here have a special sense: objects of daily life which you can find or Eric Polizzi make in minutes, yet which, if played with imaginatively, University of Massachusetts, Amherst, USA reveal surprises that keep scientists puzzling for a while. [email protected] We will see table-top demos of many such toys and visit some of the science that they open up. The common theme CP1 is singularity. Combining Krylov Subspace Recycling with Recy- Tadashi Tokieda cling Preconditioners for Sequences of Linear Sys- AN16 Abstracts 5 tems the utility of the Lavalette distribution in several dataset and discuss estimation and goodness of fit methods. Preconditioners are generally essential for fast convergence of iterative solvers. For sequences of systems, it may be Oscar Fontanelli, Pedro Miramontes advantageous to recycle (update and reuse) precondition- Facultad de Ciencias, Universidad Nacional Aut´onoma de ers. Recycling Krylov subspaces from previous systems M´exic is a complementary method for reducing computational [email protected], [email protected] cost. We examine the combination of recycling subspaces with recycling preconditioners, providing theoretical and Germinal Cocho numerical analysis. Applications include model reduction, Instituto de Fsica, Universidad Nacional Aut´onoma de tomography, and others. M´exico cocho@fisica.unam.mx Arielle K. Grim-McNally, Eric De Sturler Virginia Tech Wentian Li [email protected], [email protected] The Feinstein Institute for Medical Research [email protected] CP1 Neighbor Discovery for Algebraic Multigrid and CP2 Matrix Migration Optimizing Radioactive Contamination Monitor- ing Using Utility Functions in a Bayesian Network The idea of a neighbor — processors to whom point-to- point messages get sent/received — is core to MPI-based After an incident involving radionuclides release, the level parallelism. Finding those communication patterns re- of radioactive contamination of individuals is assessed from quires neighbor discovery, which can be quie expensive. results of bioassay monitoring. Such retrospective assess- We will focus on two computational kernels involved in al- ment is prone to uncertainty which Bayesian methods gebraic multigrid — migration of sparse matrices between are well-adapted to evaluate. An algorithm based on a processors and sparse matrix-matrix multiplication. We Bayesian network (BN) providing an initial quantification will show that for these kernels, passing additional infor- of the contamination and its associated uncertainty was de- mation during point-to-point communication can allow one veloped to optimize bioassay monitoring. The best follow- to perform neighbor discovery more efficiently. up program is then determined through a prospective util- ity function integrated in the BN. Christopher Siefert Sandia National Laboratories Leila Gharsalli [email protected] IRSN, France [email protected] CP1 Mathilde Vincent Heavy Ball Minimal Residual Method for Least- Ancient IRSN Squares Problem [email protected] The heavy ball minimal residual (HBMR) method is pre- sented for solving overdetermined least-squares problem Estelle Davesne, Eric Chojnacki, Eric Blanchardon Ax − b ,whereA is a sparse matrix. HBMR method IRSN 2 [email protected], [email protected], seeks optimal approximate solutions of the least- squares T [email protected] problem by minimizing the residual norm A r 2 over both the Krylov subspace obtained by the restarted Golub- Kahan bidiagonalization process and the information of the CP2 Krylov subspaces in the previous cycles. Numerical exper- iments are reported to show the advantages of the HBMR Modeling Extreme Weather Events method. The 2016 Blizzard brought disastrous outcomes to the Mei Yang Northeastern U.S. Using extreme value analysis to ana- University of Texas at Arlington lyze NYCs historical daily extreme snowfall data up to [email protected] the 2006-2007 winter, we will determine if predicting the Blizzard was reasonable. Initial analysis shows that time- independent extreme value models did not predict the Bliz- Ren-Cang Li zard, suggesting models need to take climate changes into University of Texas - Arlington account. We also will use data up to January 2016 to assess [email protected] return levels for future extreme events. Mintaek Lee CP2 Boise State University New Insights into Scaling Laws: The Lavalette Dis- [email protected] tribution and Its Properties We introduce a novel family of probability
Load more

Recommended publications
  • June 2014 Society Meetings Society and Events SHEPHARD PRIZE: NEW PRIZE Meetings for MATHEMATICS 2014 and Events Following a Very Generous Tions Open in Late 2014
    LONDONLONDON MATHEMATICALMATHEMATICAL SOCIETYSOCIETY NEWSLETTER No. 437 June 2014 Society Meetings Society and Events SHEPHARD PRIZE: NEW PRIZE Meetings FOR MATHEMATICS 2014 and Events Following a very generous tions open in late 2014. The prize Monday 16 June donation made by Professor may be awarded to either a single Midlands Regional Meeting, Loughborough Geoffrey Shephard, the London winner or jointly to collaborators. page 11 Mathematical Society will, in 2015, The mathematical contribution Friday 4 July introduce a new prize. The prize, to which an award will be made Graduate Student to be known as the Shephard must be published, though there Meeting, Prize will be awarded bienni- is no requirement that the pub- London ally. The award will be made to lication be in an LMS-published page 8 a mathematician (or mathemati- journal. Friday 4 July cians) based in the UK in recog- Professor Shephard himself is 1 Society Meeting nition of a specific contribution Professor of Mathematics at the Hardy Lecture to mathematics with a strong University of East Anglia whose London intuitive component which can be main fields of interest are in page 9 explained to those with little or convex geometry and tessella- Wednesday 9 July no knowledge of university math- tions. Professor Shephard is one LMS Popular Lectures ematics, though the work itself of the longest-standing members London may involve more advanced ideas. of the LMS, having given more page 17 The Society now actively en- than sixty years of membership. Tuesday 19 August courages members to consider The Society wishes to place on LMS Meeting and Reception nominees who could be put record its thanks for his support ICM 2014, Seoul forward for the award of a in the establishment of the new page 11 Shephard Prize when nomina- prize.
    [Show full text]
  • Animal Welfare and the Paradox of Animal Consciousness
    ARTICLE IN PRESS Animal Welfare and the Paradox of Animal Consciousness Marian Dawkins1 Department of Zoology, University of Oxford, Oxford, UK 1Corresponding author: e-mail address: [email protected] Contents 1. Introduction 1 2. Animal Consciousness: The Heart of the Paradox 2 2.1 Behaviorism Applies to Other People Too 5 3. Human Emotions and Animals Emotions 7 3.1 Physiological Indicators of Emotion 7 3.2 Behavioral Components of Emotion 8 3.2.1 Vacuum Behavior 10 3.2.2 Rebound 10 3.2.3 “Abnormal” Behavior 10 3.2.4 The Animal’s Point of View 11 3.2.5 Cognitive Bias 15 3.2.6 Expressions of the Emotions 15 3.3 The Third Component of Emotion: Consciousness 16 4. Definitions of Animal Welfare 24 5. Conclusions 26 References 27 1. INTRODUCTION Consciousness has always been both central to and a stumbling block for animal welfare. On the one hand, the belief that nonhuman animals suffer and feel pain is what draws many people to want to study animal welfare in the first place. Animal welfare is seen as fundamentally different from plant “welfare” or the welfare of works of art precisely because of the widely held belief that animals have feelings and experience emotions in ways that plants or inanimate objectsdhowever valuableddo not (Midgley, 1983; Regan, 1984; Rollin, 1989; Singer, 1975). On the other hand, consciousness is also the most elusive and difficult to study of any biological phenomenon (Blackmore, 2012; Koch, 2004). Even with our own human consciousness, we are still baffled as to how Advances in the Study of Behavior, Volume 47 ISSN 0065-3454 © 2014 Elsevier Inc.
    [Show full text]
  • Marvin Gaye As Vocal Composer 63 Andrew Flory
    Sounding Out Pop Analytical Essays in Popular Music Edited by Mark Spicer and John Covach The University of Michigan Press • Ann Arbor Copyright © by the University of Michigan 2010 All rights reserved Published in the United States of America by The University of Michigan Press Manufactured in the United States of America c Printed on acid-free paper 2013 2012 2011 2010 4321 No part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, or otherwise, without the written permission of the publisher. A CIP catalog record for this book is available from the British Library. Library of Congress Cataloging-in-Publication Data Sounding out pop : analytical essays in popular music / edited by Mark Spicer and John Covach. p. cm. — (Tracking pop) Includes index. ISBN 978-0-472-11505-1 (cloth : alk. paper) — ISBN 978-0-472-03400-0 (pbk. : alk. paper) 1. Popular music—History and criticism. 2. Popular music— Analysis, appreciation. I. Spicer, Mark Stuart. II. Covach, John Rudolph. ML3470.S635 2010 781.64—dc22 2009050341 Contents Preface vii Acknowledgments xi 1 Leiber and Stoller, the Coasters, and the “Dramatic AABA” Form 1 john covach 2 “Only the Lonely” Roy Orbison’s Sweet West Texas Style 18 albin zak 3 Ego and Alter Ego Artistic Interaction between Bob Dylan and Roger McGuinn 42 james grier 4 Marvin Gaye as Vocal Composer 63 andrew flory 5 A Study of Maximally Smooth Voice Leading in the Mid-1970s Music of Genesis 99 kevin holm-hudson 6 “Reggatta de Blanc” Analyzing
    [Show full text]
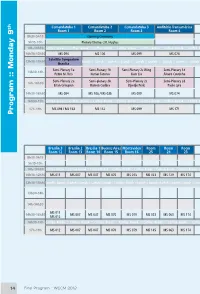
  • Program :: Monday 9
    Comandatuba 1 Comandatuba 2 Comandatuba 3 Auditório Transamérica Una Ilhéus São Paulo 3 São Paulo 2 São Paulo 1 Quito Santiago th Room 1 Room 2 Room 3 Room 4 Room 5 Room 6 Room 7 Room 8 Room 9 Room 10 Room 11 8h30-9h15 Opening Ceremony 9h15-10h Plenary Thomas J.R. Hughes 10h-10h30 Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break 10h30-12h30 MS 094 MS 106 MS 099 MS 074 MS 142 MS 133 MS 001 MS 075 MS 085 MS 002 Satellite Symposium 12h30-13h30 Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch :: Lunch Brasília Semi-Plenary 1a Semi-Plenary 1b Semi-Plenary 2c Wing Semi-Plenary 1d 13h30-14h Pedro M. Reis Kumar Tamma Kam Liu Álvaro Coutinho Semi-Plenary 2a Semi-plenary 2b Semi-Plenary 2c Semi-Plenary 2d 14h-14h30 Eitan Grinspun Ramon Codina Djordje Peric Paulo Lyra 14h30-16h30 MS 094 MS 106 / MS 035 MS 099 MS 074 MS 142 MS 133 MS 001 MS 075 MS 085 MS 002 16h30-17h Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break :: Coffee Break 17h-19h MS 094 / MS 163 MS 132 MS 099 MS 171 MS 142 / MS 005 MS 116 MS 001 MS 075 MS 085 MS 002 Program :: Monday 9 Brasília 3 Brasília 2 Brasília 1 Buenos Aires Montevideo Room Room Room Room Room Room Room Room
    [Show full text]
  • Animal Welfare Regulation in the Australian Agricultural Sector: a Legitimacy Maximising Analysis
    Animal Welfare Regulation in the Australian Agricultural Sector: A Legitimacy Maximising Analysis Jed Goodfellow LLB/BA (Hons), GDLP Macquarie Law School Macquarie University This thesis is presented for the degree of Doctor of Philosophy in Law September 2015 In dedication to each of the 605 million sentient beings used for food and fibre in Australia every year, and to the people who wish to represent their interests. Contents Abstract ........................................................................................................................... v Statement of Candidate .......................................................................................................... vi Acknowledgements ................................................................................................................. vii List of Tables and Figures ..................................................................................................... ix PART I - Setting the Regulatory Scene Chapter 1: Introduction ........................................................................................... 3 1.1 Background to research problem ....................................................................... 3 1.2 Research objectives and questions ..................................................................... 7 1.3 Methodology: the legitimacy and regulatory analytical framework .................. 8 1.3.1 Legitimacy theory ........................................................................................ 9 1.3.2 Input legitimacy
    [Show full text]
  • 14Th U.S. National Congress on Computational Mechanics
    14th U.S. National Congress on Computational Mechanics Montréal • July 17-20, 2017 Congress Program at a Glance Sunday, July 16 Monday, July 17 Tuesday, July 18 Wednesday, July 19 Thursday, July 20 Registration Registration Registration Registration Short Course 7:30 am - 5:30 pm 7:30 am - 5:30 pm 7:30 am - 5:30 pm 7:30 am - 11:30 am Registration 8:00 am - 9:30 am 8:30 am - 9:00 am OPENING PL: Tarek Zohdi PL: Andrew Stuart PL: Mark Ainsworth PL: Anthony Patera 9:00 am - 9.45 am Chair: J.T. Oden Chair: T. Hughes Chair: L. Demkowicz Chair: M. Paraschivoiu Short Courses 9:45 am - 10:15 am Coffee Break Coffee Break Coffee Break Coffee Break 9:00 am - 12:00 pm 10:15 am - 11:55 am Technical Session TS1 Technical Session TS4 Technical Session TS7 Technical Session TS10 Lunch Break 11:55 am - 1:30 pm Lunch Break Lunch Break Lunch Break CLOSING aSPL: Raúl Tempone aSPL: Ron Miller aSPL: Eldad Haber 1:30 pm - 2:15 pm bSPL: Marino Arroyo bSPL: Beth Wingate bSPL: Margot Gerritsen Short Courses 2:15 pm - 2:30 pm Break-out Break-out Break-out 1:00 pm - 4:00 pm 2:30 pm - 4:10 pm Technical Session TS2 Technical Session TS5 Technical Session TS8 4:10 pm - 4:40 pm Coffee Break Coffee Break Coffee Break Congress Registration 2:00 pm - 8:00 pm 4:40 pm - 6:20 pm Technical Session TS3 Poster Session TS6 Technical Session TS9 Reception Opening in 517BC Cocktail Coffee Breaks in 517A 7th floor Terrace Plenary Lectures (PL) in 517BC 7:00 pm - 7:30 pm Cocktail and Banquet 6:00 pm - 8:00 pm Semi-Plenary Lectures (SPL): Banquet in 517BC aSPL in 517D 7:30 pm - 9:30 pm Viewing of Fireworks bSPL in 516BC Fireworks and Closing Reception Poster Session in 517A 10:00 pm - 10:30 pm on 7th floor Terrace On behalf of Polytechnique Montréal, it is my pleasure to welcome, to Montreal, the 14th U.S.
    [Show full text]
  • Www .Ima.Umn.Edu
    ce Berkeley National Laboratory) ce Berkeley Who should attend? Industrial engineers and scientists who want to learn about modern techniques in scientific computations Researchers from academic institutions involved in multidisciplinary collaborations Organizer Robert V. Kohn Tutorial Lectures: Weinan E Leslie F. Greengard courtesy and S.Graphics J-D. Yu Sakia (Epson Research Corporation), and J.A. Sethian (Dept. and Lawren UC Berkeley of Mathematics, James A. Sethian www.ima.umn.edu The primary goal of this workshop is to facilitate the use of the best computational techniques in important industrial applications. Key developers of three of the most significant recent or emerging paradigms of computation – fast multipole methods, level set methods, and multiscale computation – will provide tutorial introductions to these classes of methods. Presentations will be particularly geared to scientists using or interested in using these approaches in industry. In addition the workshop will include research reports, poster presentations, and problem posing by industrial researchers, and offer ample time for both formal and informal discussion, related to the use of these new methods of computation. The IMA is an NSF funded Institute Schedule Weinan E received his Ph.D. from the University of California at Los Angeles in 1989. He was visiting MONDAY, MARCH 28 member at the Courant Institute from 1989 to 1991. He joined the IAS in Princeton as a long term mem- All talks are in Lecture Hall EE/CS 3-180 ber in 1992 and went on to take a faculty 8:30 Coffee and Registration position at the Courant Institute at New York Reception Room EE/CS 3-176 University in 1994.
    [Show full text]
  • Analysis-Guided Improvements of the Material Point Method
    ANALYSIS-GUIDED IMPROVEMENTS OF THE MATERIAL POINT METHOD by Michael Dietel Steffen A dissertation submitted to the faculty of The University of Utah in partial fulfillment of the requirements for the degree of Doctor of Philosophy in Computing School of Computing The University of Utah December 2009 Copyright c Michael Dietel Steffen 2009 ° All Rights Reserved THE UNIVERSITY OF UTAH GRADUATE SCHOOL SUPERVISORY COMMITTEE APPROVAL of a dissertation submitted by Michael Dietel Steffen This dissertation has been read by each member of the following supervisory committee and by majority vote has been found to be satisfactory. Chair: Robert M. Kirby Martin Berzins Christopher R. Johnson Steven G. Parker James E. Guilkey THE UNIVERSITY OF UTAH GRADUATE SCHOOL FINAL READING APPROVAL To the Graduate Council of the University of Utah: I have read the dissertation of Michael Dietel Steffen in its final form and have found that (1) its format, citations, and bibliographic style are consistent and acceptable; (2) its illustrative materials including figures, tables, and charts are in place; and (3) the final manuscript is satisfactory to the Supervisory Committee and is ready for submission to The Graduate School. Date Robert M. Kirby Chair, Supervisory Committee Approved for the Major Department Martin Berzins Chair/Dean Approved for the Graduate Council Charles A. Wight Dean of The Graduate School ABSTRACT The Material Point Method (MPM) has shown itself to be a powerful tool in the simulation of large deformation problems, especially those involving complex geometries and contact where typical finite element type methods frequently fail. While these large complex problems lead to some impressive simulations and so- lutions, there has been a lack of basic analysis characterizing the errors present in the method, even on the simplest of problems.
    [Show full text]
  • Hutnan Ethology Bulletin
    Hutnan Ethology Bulletin VOLUME 12, ISSUE 1 ISSN 0739-2036 MARCH 1997 © 1997 The International Society for Human Ethology obviously not in the interests of the slaves. Why don't they go on strike? Because the slaves are not genetically related to anything that comes out of the nest where they are now working. Any gene that tended to make them go on strike would have no possibility of being benefited by the striking action. The copies of their genes, the ·copies of these striking workers genes, would be back in the home nest, and they would be being turned out by the queen, which the striking workers left behind. So there would be no opportunity for a phenotypic effect, namely striking, to benefit germ line copies of themselves. You also write about an ant species called Monomorium santschii in which there are no workers. The queen invades a nest of another species, and then uses chemicals to induce the An Interview of workers to adopt her, and to kill their own queen. How is it possible that natural sdection Richard Dawkins did not act against such incredible deception and manipulation, which must have been going By Frans Roes, Lauriergracht 127-II, 1016 on for millions of years? RK Amsterdam, The Netherlands In any kind of arms race, it is possible for one Richard Dawkins is a zoologist and Professor of . side in the arms race to lose consistently. Public. Understanding of Science at Oxford Monomorium santschii is a very rare species. If University. Of his best-selling books, The you look back in the ancestry of the victim- Selfish Gene (1976) probably did most in species over many millions of years, many of bringing the evolutionary message home to both their ancestors may never have encountered a professional and a general readership.
    [Show full text]
  • 1 Stairway to Heaven Led Zeppelin 1971 2 Hey Jude the Beatles 1968
    1 Stairway To Heaven Led Zeppelin 1971 2 Hey Jude The Beatles 1968 3 (I Can't Get No) Satisfaction Rolling Stones 1965 4 Jailhouse Rock Elvis Presley 1957 5 Born To Run Bruce Springsteen 1975 6 I Want To Hold Your Hand The Beatles 1964 7 Yesterday The Beatles 1965 8 Peggy Sue Buddy Holly 1957 9 Imagine John Lennon 1971 10 Johnny B. Goode Chuck Berry 1958 11 Born In The USA Bruce Springsteen 1985 12 Happy Together The Turtles 1967 13 Mack The Knife Bobby Darin 1959 14 Brown Sugar Rolling Stones 1971 15 Blueberry Hill Fats Domino 1956 16 I Heard It Through The Grapevine Marvin Gaye 1968 17 American Pie Don McLean 1972 18 Proud Mary Creedence Clearwater Revival 1969 19 Let It Be The Beatles 1970 20 Nights In White Satin Moody Blues 1972 21 Light My Fire The Doors 1967 22 My Girl The Temptations 1965 23 Help! The Beatles 1965 24 California Girls Beach Boys 1965 25 Born To Be Wild Steppenwolf 1968 26 Take It Easy The Eagles 1972 27 Sherry Four Seasons 1962 28 Stop! In The Name Of Love The Supremes 1965 29 A Hard Day's Night The Beatles 1964 30 Blue Suede Shoes Elvis Presley 1956 31 Like A Rolling Stone Bob Dylan 1965 32 Louie Louie The Kingsmen 1964 33 Still The Same Bob Seger & The Silver Bullet Band 1978 34 Hound Dog Elvis Presley 1956 35 Jumpin' Jack Flash Rolling Stones 1968 36 Tears Of A Clown Smokey Robinson & The Miracles 1970 37 Addicted To Love Robert Palmer 1986 38 (We're Gonna) Rock Around The Clock Bill Haley & His Comets 1955 39 Layla Derek & The Dominos 1972 40 The House Of The Rising Sun The Animals 1964 41 Don't Be Cruel Elvis Presley 1956 42 The Sounds Of Silence Simon & Garfunkel 1966 43 She Loves You The Beatles 1964 44 Old Time Rock And Roll Bob Seger & The Silver Bullet Band 1979 45 Heartbreak Hotel Elvis Presley 1956 46 Jump (For My Love) Pointer Sisters 1984 47 Little Darlin' The Diamonds 1957 48 Won't Get Fooled Again The Who 1971 49 Night Moves Bob Seger & The Silver Bullet Band 1977 50 Oh, Pretty Woman Roy Orbison 1964 51 Ticket To Ride The Beatles 1965 52 Lady Styx 1975 53 Good Vibrations Beach Boys 1966 54 L.A.
    [Show full text]
  • Date of Event Name - Venue - Event Type
    Jay's Disco's Playlist Request Form Date Of Event Name - Venue - Event Type - Please either E-mail this form back to [email protected] 2 weeks before your event or Send it to Jay's Disco's, 72 Alexandra Road, Walsall, WS1 4DX 3 weeks before your event. If you havent had a reply from ourselves then please call us on 07919921430 at least 2 days before your event Also if you are sending a copy via post then please keep a copy as I would hate it to get lost in the post. "DO" Play "DON'T PLAY 1 I Heard It Through The Grapevine - Marvin Gaye 2 My Girl - Temptations 3 Reach Out I'll Be There - Four Tops 4 Where Did Our Love Go? - Supremes 5 What's Goin' On? - Marvin Gaye 6 Dancing in the Street - Martha & The Vandellas 7 I Want You Back - Jackson 5 8 Superstition - Stevie Wonder 9 Please Mr. Postman - Marvelettes 10 My Guy - Mary Wells 11 (Love Is Like a) Heat Wave - Martha & The Vandellas 12 Do You Love Me? - Contours 13 Let's Get It On - Marvin Gaye 14 Ain't No Mountain High Enough - Marvin Gaye & Tammi Terrell 15 The Tracks of My Tears - Smokey Robinson & The Miracles 16 Shotgun - Jr. Walker & The All Stars 17 I'll Be There - Jackson 5 18 Baby Love - Supremes 19 Papa Was a Rollin' Stone - Temptations 20 Uptight (Everything's Alright) - Stevie Wonder 21 I Can't Help Myself (Sugar Pie Honey Bunch) - Four Tops 22 The Tears of a Clown - Smokey Robinson & The Miracles 23 Stop! In the Name of Love - Supremes 24 You've Really Got a Hold On Me - Miracles 25 Just My Imagination (Running Away With Me) - Temptations 26 Baby I Need Your
    [Show full text]
  • A Free-Space Adaptive Fmm-Based Pde Solver in Three Dimensions M.Harper Langston, Leslie Greengardand Denis Zorin
    Communications in Applied Mathematics and Computational Science A FREE-SPACE ADAPTIVE FMM-BASED PDE SOLVER IN THREE DIMENSIONS M. HARPER LANGSTON, LESLIE GREENGARD AND DENIS ZORIN vol. 6 no. 1 2011 mathematical sciences publishers COMM. APP. MATH. AND COMP. SCI. Vol. 6, No. 1, 2011 msp A FREE-SPACE ADAPTIVE FMM-BASED PDE SOLVER IN THREE DIMENSIONS M. HARPER LANGSTON, LESLIE GREENGARD AND DENIS ZORIN We present a kernel-independent, adaptive fast multipole method (FMM) of arbi- trary order accuracy for solving elliptic PDEs in three dimensions with radiation and periodic boundary conditions. The algorithm requires only the ability to evaluate the Green’s function for the governing equation and a representation of the source distribution (the right-hand side) that can be evaluated at arbitrary points. The performance is accelerated in three ways. First, we construct a piecewise polynomial approximation of the right-hand side and compute far-field expansions in the FMM from the coefficients of this approximation. Second, we precompute tables of quadratures to handle the near-field interactions on adaptive octree data structures, keeping the total storage requirements in check through the exploitation of symmetries. Third, we employ shared-memory parallelization methods and load-balancing techniques to accelerate the major algorithmic loops of the FMM. We present numerical examples for the Laplace, modified Helmholtz and Stokes equations. 1. Introduction Many problems in scientific computing call for the efficient solution to linear partial differential equations with constant coefficients. On regular grids with separable Dirichlet, Neumann or periodic boundary conditions, such equations can be solved using fast, direct methods.
    [Show full text]