DOCSLIB.ORG

Data Representation in Visualisation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Data Representation in Visualisation Visualisation : Lecture 4 Data Representation in Visualisation Visualisation – Lecture 4 Taku Komura Institute for Perception, Action & Behaviour School of Informatics Taku Komura Data Representation 1 Visualisation : Lecture 4 Data Representation ● We have a system architecture for visualisation – the visualisation pipeline – rendering techniques ● Data is ........ – discrete (in representation) – structured / unstructured (e.g. grid / cloud) – of a specific dimension D (e.g. 2D / 3D) Taku Komura Data Representation 2 Visualisation : Lecture 4 Discrete vs. Continuous ● Real World is continuous ● Data is discrete – Computers are good in handling discrete data – discrete representation of a real world (of abstract) concept ● Difficult to visualise continuous shape from raw discrete sampling? – we need topology and interpolation Taku Komura Data Representation 3 Visualisation : Lecture 4 Interpolation & Topology ● If we introduce topology our visualisation of discrete data improves – The topology helps the visual system to do the interpolation Taku Komura Data Representation 4 Visualisation : Lecture 4 Topology ● Topology : relationships within the data invariant under geometric transformation (i.e. Orientation, translation) i.e. the information which vertex is connected to which edge, which face is composed of which edges , etc. Taku Komura Data Representation 5 Visualisation : Lecture 4 Interpolation & Topology ● What if these colour represented spatial temperature at these 8 discrete points? – e.g. colour scale blue(=cold)→green→red( = hot) – How easy is it to visualise the temperature field over the whole cube? Taku Komura Data Representation 6 Visualisation : Lecture 4 Interpolation & Topology ● Use interpolation to shade whole cube: – Interpolation: increasing resolution of a discrete representation by producing intermediate samples — in example: producing intermediate colour pixels over cube topology from discrete vertex samples Taku Komura Data Representation 7 Visualisation : Lecture 4 How to interpolate over a rectangle? ● Will the red color dot on the right lower corner affect the color of the point near the left top? Taku Komura Data Representation 8 Visualisation : Lecture 4 Importance of representation ● What happens if we change the representation? ● Discrete data samples remain the same – topology has changed ⇒ effects interpolation ⇒ effects visualisation Taku Komura Data Representation 9 Visualisation : Lecture 4 How to interpolate in this case? ● Will the red color dot on the right lower corner affect the color of point near the left top? Taku Komura Data Representation 10 Visualisation : Lecture 4 Interpolation in digital images ● Some digital cameras use interpolation to produce a larger image than the sensor captured or to create digital zoom. ● Also using the topology data No interpolation Taku Komura With interpolation Data Representation 11 Visualisation : Lecture 4 Topological Dimension • Data has an inherent topological dimension – I.e minimum number of independent continuous variables needed to specify the location inside the data – Points : 0D, – curves : 1D, – surfaces : 2D, – volumes : 3D – Time dependent volumes : 4D Taku Komura Data Representation 12 Visualisation : Lecture 4 Data Representation ● Data objects : structure + value – referred to as datasets Abstract Concrete (e.g. VTK) Structure - Topology Consists of - Geometry Cells, points (grid) ————————— ————————— Data Attributes Scalars, vectors Normals, texture coordinates, tensors etc Taku Komura Data Representation 13 Visualisation : Lecture 4 What is a dataset? ● Dataset consists of 2 main components – structure of the data – value – attributes associated to particular parts of the structure – structure gives spatial meaning to the attributes values = { blue, green, green, green, green, green, turquoise, red} – – – attributes alone are meaningless without structure Taku Komura Data Representation 14 Visualisation : Lecture 4 Structure of Data ● Structure has 2 main parts – topology : — determines interpolation required for visualisation — “shape” of data OR – geometry — instantiation of the topology — specific position of points in geometric space Taku Komura Data Representation 15 Visualisation : Lecture 4 Concrete Representation of Datasets ● Points specify where the data is known – specify geometry in ℝN ● Cells allow us to interpolate between points – specify topology of points Point with known attribute data (i.e. colour ≈ temperature) Cell (i.e. the triangle) over which we can interpolate data. Taku Komura Data Representation 16 Visualisation : Lecture 4 Cells ● Fundamental building blocks of the shapes ● Various Cell Types – defined by topological dimension – specified as an ordered point list – primary or composite cells — composite : consists of one or more primary cells Taku Komura Data Representation 17 Visualisation : Lecture 4 Zero-dimensional cell types ● Vertex – Primary zero-dimensional cell – Definition: single point ● Polyvertex – Composite zero-dimensional cell — composite : comprises of several vertex cells – Definition: arbitrarily ordered set of points Taku Komura Data Representation 18 Visualisation : Lecture 4 One-dimensional cell types ● Line – Primary one-dimensional cell type – Definition: 2 points, direction is from first to second point. ● Polyline – Composite one-dimensional cell type – Definition: an ordered set of n+1 points, where n is the number of lines in the polyline Taku Komura Data Representation 19 Visualisation : Lecture 4 Two-dimensional cell types - 1 ● Triangle – Primary 2D cell type – Definition: counter-clockwise ordering of 3 points — order of the points specifies the direction of the surface normal ● Triangle strip – Composite 2D cell consisting of a strip of triangles – Definition: ordered list of n+2 points — n is the number of triangles ● Quadrilateral – Primary 2D cell type – Definition: ordered list of four points lying in a plane — constraints: convex + edges must not intersect Taku Komura Data Representation 20 Visualisation : Lecture 4 Two-dimensional cell types - 2 ● Pixel – Primary 2D cell, consisting of 4 points — topologically equivalent to a quadrilateral — constraints: perpendicular edges; axis aligned – numbering is in increasing axis coordinates ● Polygon – Primary 2D cell type – Definition: ordered list of 3 or more points — constraint: may not self-intersect Taku Komura Data Representation 21 Visualisation : Lecture 4 Three-dimensional cell types ● Tetrahedron – Definition: list of 4 non-planar points — Six edges, four faces ● Hexahedron – Definition: ordered list of 8 points — six quadrilateral faces, 12 edges, 8 vertices — constraint: edges and faces must not intersect ● Voxel – Topologically equivalent to Hexahedron – constraint: each face is perpendicular to a coordinate axis – “3D pixels” Taku Komura Data Representation 22 Visualisation : Lecture 4 Example Applications & Cell Types ● Lines – Segmentation of tissues from images ● Pixels – images, regular height map data ● Quadrilaterals – Finite element analysis ● Voxels : “3D pixels” – volume data : medical scanners Taku Komura Data Representation 23 Visualisation : Lecture 4 Attribute Data ● Information associated with data topology – usually associated to points or cells ● Examples : – temperature, wind speed, humidity, rain fall (meteorology) – heat flux, stress, vibration (engineering) – surface normal, colour (computer graphics) ● Usually categorised into specific types: – scalar (1D) – vector (commonly 2D or 3D; ND in ℝN) – tensor (N dimensional array) Taku Komura Data Representation 24 Visualisation : Lecture 4 Attribute Data : Scalar ● Single valued data at each location ozone levels elevation from reference plane – volume density (MRI) – simplest and most common form of visualisation data Taku Komura Data Representation 25 Visualisation : Lecture 4 Attribute Data : Vector Data ● Magnitude and direction at each location – 3D triplet of values (i, j, k) Wind Speed Force / Displacement Magnetic Field – Also Normals – vectors of unit length (magnitude = 1) Taku Komura Data Representation 26 Visualisation : Lecture 4 Attribute Data : Tensor Data ● K-dimensional array at each location – Generalisation of vectors and matrices – Tensor of rank k can be considered a k-dimensional table — Rank 0 is a scalar — Rank 1 is a vector — Rank 2 is a matrix — Rank 3 is a regular 3D array ● Tensor visualisation is an active area of research – covered later in lectures Taku Komura Data Representation 27 Visualisation : Lecture 4 Types of Dataset ● Defined by structure type: regular or irregular ● If there is a mathematical relationship between the point & cell positions it is regular – if the points are regular, the geometry is regular – if the cells are regular, the topology is regular ● Regular data can be implicitly represented – saves storage and computation (e.g. grid based representation) Taku Komura Data Representation 28 Visualisation : Lecture 4 Regular : Structured Points ● Points & cells arranged in a regular grid – axis aligned grid – for line elements (1D), pixels (2D) or voxels (3D) – e.g. images (2D), medical scanners (3D) – regular topology and geometry — uniform, equally spaced, axis aligned cells Taku Komura Data Representation 29 Visualisation : Lecture 4 Regular : Rectilinear Grid ● Points and cells arranged in a regular grid – topology is regular – geometry is partially regular – points are arranged along the axes but the spacing may vary – e.g. log-scale Taku Komura Data Representation 30 Visualisation
Load more

Recommended publications
  • ICES REPORT 14-22 Characterization, Enumeration and Construction Of
    ICES REPORT 14-22 August 2014 Characterization, Enumeration and Construction of Almost-regular Polyhedra by Muhibur Rasheed and Chandrajit Bajaj The Institute for Computational Engineering and Sciences The University of Texas at Austin Austin, Texas 78712 Reference: Muhibur Rasheed and Chandrajit Bajaj, "Characterization, Enumeration and Construction of Almost-regular Polyhedra," ICES REPORT 14-22, The Institute for Computational Engineering and Sciences, The University of Texas at Austin, August 2014. Characterization, Enumeration and Construction of Almost-regular Polyhedra Muhibur Rasheed and Chandrajit Bajaj Center for Computational Visualization Institute of Computational Engineering and Sciences The University of Texas at Austin Austin, Texas, USA Abstract The symmetries and properties of the 5 known regular polyhedra are well studied. These polyhedra have the highest order of 3D symmetries, making them exceptionally attractive tem- plates for (self)-assembly using minimal types of building blocks, from nanocages and virus capsids to large scale constructions like glass domes. However, the 5 polyhedra only represent a small number of possible spherical layouts which can serve as templates for symmetric assembly. In this paper, we formalize the notion of symmetric assembly, specifically for the case when only one type of building block is used, and characterize the properties of the corresponding layouts. We show that such layouts can be generated by extending the 5 regular polyhedra in a sym- metry preserving way. The resulting family remains isotoxal and isohedral, but not isogonal; hence creating a new class outside of the well-studied regular, semi-regular and quasi-regular classes and their duals Catalan solids and Johnson solids. We also show that this new family, dubbed almost-regular polyhedra, can be parameterized using only two variables and constructed efficiently.
    [Show full text]
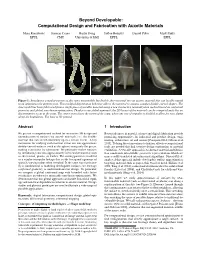
  • Omputational Design and Fabrication with Auxetic Materials
    Beyond Developable: Computational Design and Fabrication with Auxetic Materials Mina Konakovic´ Keenan Crane Bailin Deng Sofien Bouaziz Daniel Piker Mark Pauly EPFL CMU University of Hull EPFL EPFL Figure 1: Introducing a regular pattern of slits turns inextensible, but flexible sheet material into an auxetic material that can locally expand in an approximately uniform way. This modified deformation behavior allows the material to assume complex double-curved shapes. The shoe model has been fabricated from a single piece of metallic material using a new interactive rationalization method based on conformal geometry and global, non-linear optimization. Thanks to our global approach, the 2D layout of the material can be computed such that no discontinuities occur at the seam. The center zoom shows the region of the seam, where one row of triangles is doubled to allow for easy gluing along the boundaries. The base is 3D printed. Abstract 1 Introduction We present a computational method for interactive 3D design and Recent advances in material science and digital fabrication provide rationalization of surfaces via auxetic materials, i.e., flat flexible promising opportunities for industrial and product design, engi- material that can stretch uniformly up to a certain extent. A key neering, architecture, art and science [Caneparo 2014; Gibson et al. motivation for studying such material is that one can approximate 2015]. To bring these innovations to fruition, effective computational doubly-curved surfaces (such as the sphere) using only flat pieces, tools are needed that link creative design exploration to material making it attractive for fabrication. We physically realize surfaces realization. A versatile approach is to abstract material and fabrica- by introducing cuts into approximately inextensible material such tion constraints into suitable geometric representations which are as sheet metal, plastic, or leather.
    [Show full text]
  • Generating Apparently-Random Colour Patterns
    Computational Aesthetics in Graphics, Visualization, and Imaging (2012) D. Cunningham and D. House (Editors) Random Discrete Colour Sampling Henrik Lieng Christian Richardt Neil A. Dodgson Generating apparently-randomUniversity of Cambridge colour patterns Used with permission of the authors Figure 1: We present an algorithm that distributes colours randomly using a human-centric definition of randomness. Left: Colours distributed using Matlab’s random-number generator. Middle: Result of our algorithm. Notice that our algorithm does not produce any distinctive patterns. Right: An image similar to one of Damien Hirst’s spot paintings. Abstract Apparently-random distributions of colours in a discrete setting have been used by many artists and craftsmen in the past century. Manual colourisation is a tedious and difficult process. Automatic colourisation, on the other hand, tends not to not look ‘random’ to a human, as randomly-generated clusters and patterns stimulate human perception and break the appearance of randomness. We propose an algorithm that minimises these apparent patterns, making the distribution of colours look as if they have been distributed randomly by a human. We show that our approach is superior to current solutions, especially for small numbers of colours. Our algorithm is easily extendible to non-regular patterns in any coordinate system. Categories and Subject Descriptors (according to ACM CCS): I.3.8 [Computer Graphics]: Applications; I.3.m [Com- puter Graphics]: Miscellaneous—Visual Arts; J.5 [Arts and Humanities]: Fine Arts. 1. Introduction Random colour sampling in the spatially discrete space was used in the early twentieth-century by numerous artists such as Jean Arp, Sophie Tauber and Vilmos Huszár.
    [Show full text]
  • Eindhoven University of Technology MASTER Lateral Stiffness Of
    Eindhoven University of Technology MASTER Lateral stiffness of hexagrid structures de Meijer, J.H.M. Award date: 2012 Link to publication Disclaimer This document contains a student thesis (bachelor's or master's), as authored by a student at Eindhoven University of Technology. Student theses are made available in the TU/e repository upon obtaining the required degree. The grade received is not published on the document as presented in the repository. The required complexity or quality of research of student theses may vary by program, and the required minimum study period may vary in duration. General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain ‘Lateral Stiffness of Hexagrid Structures’ - Master’s thesis – - Main report – - A 2012.03 – - O 2012.03 – J.H.M. de Meijer 0590897 July, 2012 Graduation committee: Prof. ir. H.H. Snijder (supervisor) ir. A.P.H.W. Habraken dr.ir. H. Hofmeyer Eindhoven University of Technology Department of the Built Environment Structural Design Preface This research forms the main part of my graduation thesis on the lateral stiffness of hexagrids. It explores the opportunities of a structural stability system that has been researched insufficiently.
    [Show full text]
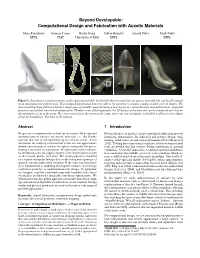
  • Beyond Developable: Omputational Design and Fabrication with Auxetic Materials
    Beyond Developable: Computational Design and Fabrication with Auxetic Materials Mina Konakovic´ Keenan Crane Bailin Deng Sofien Bouaziz Daniel Piker Mark Pauly EPFL CMU University of Hull EPFL EPFL Figure 1: Introducing a regular pattern of slits turns inextensible, but flexible sheet material into an auxetic material that can locally expand in an approximately uniform way. This modified deformation behavior allows the material to assume complex double-curved shapes. The shoe model has been fabricated from a single piece of metallic material using a new interactive rationalization method based on conformal geometry and global, non-linear optimization. Thanks to our global approach, the 2D layout of the material can be computed such that no discontinuities occur at the seam. The center zoom shows the region of the seam, where one row of triangles is doubled to allow for easy gluing along the boundaries. The base is 3D printed. Abstract 1 Introduction We present a computational method for interactive 3D design and Recent advances in material science and digital fabrication provide rationalization of surfaces via auxetic materials, i.e., flat flexible promising opportunities for industrial and product design, engi- material that can stretch uniformly up to a certain extent. A key neering, architecture, art and science [Caneparo 2014; Gibson et al. motivation for studying such material is that one can approximate 2015]. To bring these innovations to fruition, effective computational doubly-curved surfaces (such as the sphere) using only flat pieces, tools are needed that link creative design exploration to material making it attractive for fabrication. We physically realize surfaces realization. A versatile approach is to abstract material and fabrica- by introducing cuts into approximately inextensible material such tion constraints into suitable geometric representations which are as sheet metal, plastic, or leather.
    [Show full text]
  • Visualization of Regular Maps
    Symmetric Tiling of Closed Surfaces: Visualization of Regular Maps Jarke J. van Wijk Dept. of Mathematics and Computer Science Technische Universiteit Eindhoven [email protected] Abstract The first puzzle is trivial: We get a cube, blown up to a sphere, which is an example of a regular map. A cube is 2×4×6 = 48-fold A regular map is a tiling of a closed surface into faces, bounded symmetric, since each triangle shown in Figure 1 can be mapped to by edges that join pairs of vertices, such that these elements exhibit another one by rotation and turning the surface inside-out. We re- a maximal symmetry. For genus 0 and 1 (spheres and tori) it is quire for all solutions that they have such a 2pF -fold symmetry. well known how to generate and present regular maps, the Platonic Puzzle 2 to 4 are not difficult, and lead to other examples: a dodec- solids are a familiar example. We present a method for the gener- ahedron; a beach ball, also known as a hosohedron [Coxeter 1989]; ation of space models of regular maps for genus 2 and higher. The and a torus, obtained by making a 6 × 6 checkerboard, followed by method is based on a generalization of the method for tori. Shapes matching opposite sides. The next puzzles are more challenging. with the proper genus are derived from regular maps by tubifica- tion: edges are replaced by tubes. Tessellations are produced us- ing group theory and hyperbolic geometry. The main results are a generic procedure to produce such tilings, and a collection of in- triguing shapes and images.
    [Show full text]
  • A Principled Approach to the Modelling of Kagome Weave Patterns for the Fabrication of Interlaced Lattice Structures Using Straight Strips
    Beyond the basket case: A principled approach to the modelling of kagome weave patterns for the fabrication of interlaced lattice structures using straight strips. Phil Ayres, Alison Grace Martin, Mateusz Zwierzycki Phil Ayres [email protected] CITA, Denmark Alison Grace Martin [email protected] Independant 3D Weaver, Italy Mateusz Zwierzycki [email protected] The Object, Poland Keywords: Kagome, triaxial weaving, basket weaving, textiles, mesh topology, mesh valence, mesh dual, fabrication, constraint modelling, constraint based simulation, design computation 72 AAG2018 73 Abstract This paper explores how computational methods of representation can support and extend kagome handcraft towards the fabrication of interlaced lattice structures in an expanded set of domains, beyond basket making. Through reference to the literature and state of the art, we argue that the instrumentalisation of kagome principles into computational design methods is both timely and relevant; it addresses a growing interest in such structures across design and engineering communities; it also fills a current gap in tools that facilitate design and fabrication investigation across a spectrum of expertise, from the novice to the expert. The paper describes the underlying topological and geometrical principles of kagome weave, and demonstrates the direct compatibility of these principles to properties of computational triangular meshes and their duals. We employ the known Medial Construction method to generate the weave pattern, edge ‘walking’ methods to consolidate geometry into individual strips, physics based relaxation to achieve a materially informed final geometry and projection to generate fabri- cation information. Our principle contribution is the combination of these methods to produce a principled workflow that supports design investigation of kagome weave patterns with the constraint of being made using straight strips of material.
    [Show full text]
  • A Continuous Coordinate System for the Plane by Triangular Symmetry
    Article A Continuous Coordinate System for the Plane by Triangular Symmetry Benedek Nagy 1,* and Khaled Abuhmaidan 2 Department of Mathematics, Faculty of Arts and Sciences, Eastern Mediterranean University, via Mersin 10, Turkey, Famagusta 99450, North Cyprus; [email protected] * Correspondence: [email protected] Received: 20 December 2018; Accepted: 31 January 2019; Published: 9 February 2019 Abstract: The concept of the grid is broadly used in digital geometry and other fields of computer science. It consists of discrete points with integer coordinates. Coordinate systems are essential for making grids easy to use. Up to now, for the triangular grid, only discrete coordinate systems have been investigated. These have limited capabilities for some image-processing applications, including transformations like rotations or interpolation. In this paper, we introduce the continuous triangular coordinate system as an extension of the discrete triangular and hexagonal coordinate systems. The new system addresses each point of the plane with a coordinate triplet. Conversion between the Cartesian coordinate system and the new system is described. The sum of three coordinate values lies in the closed interval [−1, 1], which gives many other vital properties of this coordinate system. Keywords: barycentric coordinate system; coordinate system; hexagonal grid; triangular grid; tri- hexagonal grid; transformations 1. Introduction The concept of the grid is essential and heavily used in digital geometry and in digital image processing. A grid is comprised of discrete points addressed with integer vectors. There are three regular tessellations of the plane, which define the square, hexagonal, and triangular grids (named after the form of the pixels used as tiles) [1].
    [Show full text]
  • Direct Generation of Regular-Grid Ground Surface Map from In-Vehicle Stereo Image Sequences
    2013 IEEE International Conference on Computer Vision Workshops Direct Generation of Regular-Grid Ground Surface Map From In-Vehicle Stereo Image Sequences Shigeki Sugimoto Kouma Motooka Masatoshi Okutomi Tokyo Institute of Technology 2–12–1–S5–22 Ookayama, Meguro-ku, Tokyo, 153–0834 Japan [email protected], [email protected], [email protected] Abstract ous real-time robot applications, including traversable area detection, path planning, and map extension. Our ultimate We propose a direct method for incrementally estimat- goal here is to develop an efficient method for incrementally ing a regular-grid ground surface map from stereo image estimating a DEM of a large ground area, no matter whether sequences captured by nearly front-looking stereo cameras, the target ground is off-road or not, from stereo image se- taking illumination changes on all images into considera- quences captured by in-vehicle nearly-front-looking stereo tion. At each frame, we simultaneously estimate a camera cameras. motion and vertex heights of the regular mesh, composed A DEM can be estimated by fitting a point cloud to a of piecewise triangular patches, drawn on a level plane in regular-grid surface model. Considered with the require- the ground coordinate system, by minimizing a cost repre- ment of computational efficiency in robotics, a possible senting the differences of the photometrically transformed choice is to fit a regular-grid surface to the sparse point pixel values in homography-related projective triangular cloud estimated by an efficient stereo SLAM technique (e.g. patches over three image pairs in a two-frame stereo im- [4, 8]), or to the denser point cloud estimated at each frame age sequence.
    [Show full text]
  • Recursive Tilings and Space-Filling Curves with Little Fragmentation
    Recursive tilings and space-filling curves with little fragmentation Herman Haverkort∗ October 24, 2018 Abstract This paper defines the Arrwwid number of a recursive tiling (or space-filling curve) as the smallest number a such that any ball Q can be covered by a tiles (or curve sections) with total volume O(volume(Q)). Recursive tilings and space-filling curves with low Arrwwid numbers can be applied to optimise disk, memory or server access patterns when processing sets of points in Rd. This paper presents recursive tilings and space-filling curves with optimal Arrwwid numbers. For d 3, we see that regular cube tilings and space-filling curves cannot have optimal Arrwwid≥ number, and we see how to construct alternatives with better Arrwwid numbers. 1 Introduction 1.1 The problem Consider a set of data points in a bounded region U of R2, stored on disk. A standard operation on such point sets is to retrieve all points that lie inside a certain query range, for example a circle or a square. To prevent large delays because of disk head movements while answering such queries, it is desirable that the points are stored on disk in a clustered way [2, 9, 10, 11, 15]. Similar considerations arise when storing spatial data in certain types of distributed networks [19] or when scanning spatial objects to render them as a raster image; in the latter case it is desirable that the pixels that cover any particular object are scanned in a clustered way, so that the object does not have to be brought into cache too often [21].
    [Show full text]
  • A Continuous Coordinate System for the Plane by Triangular Symmetry
    S S symmetry Article A Continuous Coordinate System for the Plane by Triangular Symmetry Benedek Nagy * and Khaled Abuhmaidan Department of Mathematics, Faculty of Arts and Sciences, Eastern Mediterranean University, via Mersin 10, Turkey, Famagusta 99450, North Cyprus; [email protected] * Correspondence: [email protected] Received: 20 December 2018; Accepted: 31 January 2019; Published: 9 February 2019 Abstract: The concept of the grid is broadly used in digital geometry and other fields of computer science. It consists of discrete points with integer coordinates. Coordinate systems are essential for making grids easy to use. Up to now, for the triangular grid, only discrete coordinate systems have been investigated. These have limited capabilities for some image-processing applications, including transformations like rotations or interpolation. In this paper, we introduce the continuous triangular coordinate system as an extension of the discrete triangular and hexagonal coordinate systems. The new system addresses each point of the plane with a coordinate triplet. Conversion between the Cartesian coordinate system and the new system is described. The sum of three coordinate values lies in the closed interval [−1, 1], which gives many other vital properties of this coordinate system. Keywords: barycentric coordinate system; coordinate system; hexagonal grid; triangular grid; tri-hexagonal grid; transformations 1. Introduction The concept of the grid is essential and heavily used in digital geometry and in digital image processing. A grid is comprised of discrete points addressed with integer vectors. There are three regular tessellations of the plane, which define the square, hexagonal, and triangular grids (named after the form of the pixels used as tiles) [1].
    [Show full text]
  • Omputational Design and Fabrication with Auxetic Materials
    This is an Open Access document downloaded from ORCA, Cardiff University's institutional repository: http://orca.cf.ac.uk/98566/ This is the author’s version of a work that was submitted to / accepted for publication. Citation for final published version: Konaković, Mina, Crane, Keenan, Deng, Bailin, Bouaziz, Sofien, Piker, Daniel and Pauly, Mark 2016. Beyond developable: Computational design and fabrication with auxetic materials. ACM Transactions on Graphics 35 (4) , 89. 10.1145/2897824.2925944 file Publishers page: http://dx.doi.org/10.1145/2897824.2925944 <http://dx.doi.org/10.1145/2897824.2925944> Please note: Changes made as a result of publishing processes such as copy­editing, formatting and page numbers may not be reflected in this version. For the definitive version of this publication, please refer to the published source. You are advised to consult the publisher’s version if you wish to cite this paper. This version is being made available in accordance with publisher policies. See http://orca.cf.ac.uk/policies.html for usage policies. Copyright and moral rights for publications made available in ORCA are retained by the copyright holders. To appear in ACM TOG 35(4). Beyond Developable: Computational Design and Fabrication with Auxetic Materials Mina Konakovic´ Keenan Crane Bailin Deng Sofien Bouaziz Daniel Piker Mark Pauly EPFL CMU University of Hull EPFL EPFL Figure 1: Introducing a regular pattern of slits turns inextensible, but flexible sheet material into an auxetic material that can locally expand in an approximately uniform way. This modified deformation behavior allows the material to assume complex double-curved shapes.
    [Show full text]