DOCSLIB.ORG

A Fast Method of Flood Discharge Estimation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Fast Method of Flood Discharge Estimation HYDROLOGICAL PROCESSES Hydrol. Process. 18, 1671–1684 (2004) Published online 8 March 2004 in Wiley InterScience (www.interscience.wiley.com). DOI: 10.1002/hyp.1476 A fast method of flood discharge estimation Yen-Chang Chen1* and Chao-Lin Chiu2 1 Department of Civil Engineering, National Taipei University of Technology, Taipei, Taiwan 2 Department of Civil and Environmental Engineering, University of Pittsburgh, Pittsburgh, PA 15261, USA Abstract: Discharge, especially during flood periods, is among the most important information necessary for flood control, water resources planning and management. Owing to the high flood velocities, flood discharge usually cannot be measured efficiently by conventional methods, which explains why records of flood discharge are scarce or do not exist for the watersheds in Taiwan. A fast method of flood discharge estimation is presented. The greatest advantage of the proposed method is its application to estimate flood discharge that cannot be measured by conventional methods. It has as its basis the regularity of open-channel flows, i.e. that nature maintains a constant ratio of mean to maximum velocities at a given channel section by adjusting the velocity distribution and the channel geometry. The maximum velocity at a given section can be determined easily over a single vertical profile, which tends to remain invariant with time and discharge, and can be converted to the mean velocity of the entire cross-section by multying by the constant ratio. Therefore the mean velocity is a common multiple of maximum velocity and the mean/maximum velocity ratio. The channel cross-sectional area can be determined from the gauge height, the water depth at the y-axis or the product of the channel width multiplied by the water depth at the y-axis. Then the most commonly used method, i.e. the velocity–area method, which determines discharge as the product of the cross-sectional area multiplied by mean velocity, is applied to estimate the flood discharge. Only a few velocity measurements on the y-axis are necessary to estimate flood discharge. Moreover the location of the y-axis will not vary with time and water stage. Once the relationship of mean and maximum velocities is established, the flood estimation can be determined efficiently. This method avoids exposure to hazardous environments and sharply reduces the measurement time and cost. The method can be applied in both high and low flows in rivers. Available laboratory flume and stream-flow data are used to illustrate accuracy and reliability, and results show that this method can quickly and accurately estimate flood discharges. Copyright 2004 John Wiley & Sons, Ltd. KEY WORDS discharge; entropy; flood estimation; mean/maximum velocity ratio; probability INTRODUCTION Discharge, the volume of water flowing through a cross-section of a stream in a given amount of time provides useful information for understanding hydrological processes. These data are very useful for water resources planning, design of hydraulic structures, flood control and decision making. A continuous record of discharge and stage can be used to construct a stage–discharge rating curve that is the most commonly used method to estimate discharge. A stage–discharge rating curve commonly obeys the equation of the form (Rantz, 1982b) Q D pG eN 1 where Q is the discharge that is usually made by current meter, p and N are constants, G is the stage and e is the water stage of zero flow. Under uniform flow conditions, discharge is then obtained by the measured stage and stage–discharge rating curve. However, a large portion of the annual transportation of water and sediment occurs during floods. It is particularly important to make discharge measurements when stream * Correspondence to: Yen-Chang Chen, Department of Civil Engineering, National Taipei University of Technology, Taipei, Taiwan. E-mail: [email protected] Copyright 2004 John Wiley & Sons, Ltd. 1672 Y.-C. CHEN AND C.-L. CHIU stages are high. Such measurements form the basis for flood warning, flood forecasting, reservoir operation and estimates of annual flow volumes. The stage–discharge relationship is subject to shifts as a result of flood wave during high water. Owing to the energy slope varying with time, the stage–discharge rating curve cannot be used to estimate discharge when backwater or highly unsteady flow exits. During a flood period, which is invariably unsteady, the stage–discharge relation is a loop as described in Figure 1, which shows that at a given water level the stage–discharge relationship obtained during steady flow periods tends to underestimate the discharge when the flow is rising, and overestimate it when the flow is subsiding. The individual conditions of an unsteady flow have individual energy slopes. Each individual flood should have an individual loop. Each loop therefore can only display only an individual flood. Consequently, it would be difficult to estimate flood discharge accurately by using a stage–discharge rating curve. Many indirect methods (Rantz, 1982b; Bureau of Reclamation, 1997) are used to estimate flood discharge. The slope–area method, which makes use of empirical equations along with the energy slope, is the most commonly used technique to make determinations of peak discharge. The channel-geometry method, which relies on discharge and channel dimensions, is used to estimate mean annual flood (Wharton and Tomlinson, 1999). However, it is difficult to measure real-time flood discharge accurately. The indirect methods cannot be of sufficient accuracy even when the flood discharge is estimated by floats (Chow, 1964). Floats are used under conditions for which no conventional method is available. Moreover flood discharge estimated by indirect methods is unreliable (Quick, 1991) and usually cannot be verified. The current-meter method is the most popular, convenient and widely used direct method of discharge measurement. The concept of the current-meter method is to divide the cross-section of an open channel into several elemental strips, and measure the velocities and depths by current meter and cable at the centre of each strip. The discharge of the stream cross-section is computed by using the mid-section or mean-section methods. The disadvantages of the current-meter method are that they are costly, labour intensive and tedious. Thus flood discharge measurement is difficult using the current-meter method. The moving-boat method is usually used to measure discharge rapidly on large steams and estuaries. However, it is frequently impractical and dangerous to use the moving-boat method during floods. Accurate 30 Unsteady flow in flume with unvegetated flood plain (Tu et al. 1995) Observed data (5) 25 Variation with time (4) t(s) (3) (1) 99 (2) (2) 100 (1) 20 (3) 105 (4) 120 (5) 150 Steady (6) (6) 200 (7) 220 15 (8) 250 (7) Q (l/s) (9) 254 (8) 10 (9) 5 0 45678910 D (cm) Figure 1. Stage–discharge loop during a flood simulated in the laboratory. Reproduced from Chiu and Chen, 2003 Copyright 2004 John Wiley & Sons, Ltd. Hydrol. Process. 18, 1671–1684 (2004) FLOOD DISCHARGE ESTIMATION 1673 estimation of flood discharge requires velocity sampling and measurement of water depths across the channel. Measuring flood discharge during highly unsteady flow has to be completed as rapidly as possible, owing to the fact that flow conditions change rapidly. Flood discharge measurement can be hazardous to personnel and instruments. In order to avoid exposure to the hazardous environment too long, some non-contact methods (Spicer et al., 1997; Herschy, 1999; Costa et al., 2000) that do not involve immersing equipment in the stream have been developed to measure flood discharge. They measure only water surface velocities. A surface-velocity coefficient of 0Ð85 or 0Ð86 is preferred to convert water surface velocity to mean velocity when a surface-velocity method is used (Rantz, 1982a). However, the maximum velocity usually occurs beneath the water surface during flood periods. The higher the water stage is, the deeper the location of maximum velocity. It is, thus, easy to underestimate flood discharges by using non-contact methods. Figure 2 shows the velocity distribution of unsteady flow. The mean velocity is 54Ð1 cm/s, and the maximum velocity occurs beneath the water surface at around 0Ð6 depth. If the mean velocity is estimated by non-contact methods, and the surface-velocity coefficient 0Ð85 is used, it will be underestimated and be only 41Ð1 cm/s. Consequently, flood discharge cannot be determined easily and accurately using conventional methods, particularly in wide open-channels. Until recently, a key limitation to understanding flood flow has been the difficulty and expense associated with using conventional methods. Owing to rapid change of flow conditions allowing very little time for measurements, new techniques have been applied to measure velocity quickly (Klein et al., 1993; Schultz, 1996; Callede et al., 2000; Sulzer et al., 2002). However, a new method to determine flood discharge efficiently is still required. A fast method of flood discharge measurement that is efficient and requires only a small number of velocity samples is preferred. (Chen and Chiu, 2002) have successfully used an efficient method to estimate discharge in tidal streams with the strong effects of turbulent flow. The concept of the method presented in this study is to attain efficiency of discharge measurements by observing and understanding the physical process of flood flow and by taking advantage of regularities recognizable in the flow. Discharge through a cross-section in a natural channel is estimated from the mean velocity in the section and the cross- sectional area. The method proposed is based on the constant ratio of mean to maximum velocities (Chiu and 8 Flume Data (Tu et al., 1995) Water in unvegetated flood plain Surface velocity = 48.4 cm/s 7 Unsteady flow, t=120 s Φ=0.78 umax=59.1 cm/s 6 D=8.4 cm h=5.4 cm h/D=0.645 5 Mean velocity = 54.1 cm/s Mean velocity by surface-velocity method = 41.1 cm/s 4 y (cm) 3 2 1 0 0 10203040506070 u (cm/s) Figure 2.
Load more

Recommended publications
  • Class 14: Basic Hydrograph Analysis Class 14: Hydrograph Analysis
    Engineering Hydrology Class 14: Basic Hydrograph Analysis Class 14: Hydrograph Analysis Learning Topics and Goals: Objectives 1. Explain how hydrographs relate to hyetographs Hydrograph 2. Create DRO (direct runoff) hydrographs by separating baseflow Description 3. Relate runoff volume to watershed area and create UH (next time) Unit Hydrographs Separating Baseflow DRO Hydrographs Ocean Class 14: Hydrograph Analysis Learning Gross rainfall = depression storage + Objectives evaporation + infiltration Hydrograph + surface runoff Description Unit Hydrographs Separating Baseflow Rainfall excess = (gross rainfall – abstractions) DRO = Direct Runoff = DRO Hydrographs = net rainfall with the primary abstraction being infiltration (i.e., assuming depression storage is small and evaporation can be neglected) Class 14: Hydrograph Hydrograph Defined Analysis Learning • a hydrograph is a plot of the Objectives variation of discharge with Hydrograph Description respect to time (it can also be Unit the variation of stage or other Hydrographs water property with respect to Separating time) Baseflow DRO • determining the amount of Hydrographs infiltration versus the amount of runoff is critical for hydrograph interpretation Class 14: Hydrograph Meteorological Factors Analysis Learning • Rainfall intensity and pattern Objectives • Areal distribution of rainfall Hydrograph • Size and duration of the storm event Description Unit Physiographic Factors Hydrographs Separating • Size and shape of the drainage area Baseflow • Slope of the land surface and channel
    [Show full text]
  • River Dynamics 101 - Fact Sheet River Management Program Vermont Agency of Natural Resources
    River Dynamics 101 - Fact Sheet River Management Program Vermont Agency of Natural Resources Overview In the discussion of river, or fluvial systems, and the strategies that may be used in the management of fluvial systems, it is important to have a basic understanding of the fundamental principals of how river systems work. This fact sheet will illustrate how sediment moves in the river, and the general response of the fluvial system when changes are imposed on or occur in the watershed, river channel, and the sediment supply. The Working River The complex river network that is an integral component of Vermont’s landscape is created as water flows from higher to lower elevations. There is an inherent supply of potential energy in the river systems created by the change in elevation between the beginning and ending points of the river or within any discrete stream reach. This potential energy is expressed in a variety of ways as the river moves through and shapes the landscape, developing a complex fluvial network, with a variety of channel and valley forms and associated aquatic and riparian habitats. Excess energy is dissipated in many ways: contact with vegetation along the banks, in turbulence at steps and riffles in the river profiles, in erosion at meander bends, in irregularities, or roughness of the channel bed and banks, and in sediment, ice and debris transport (Kondolf, 2002). Sediment Production, Transport, and Storage in the Working River Sediment production is influenced by many factors, including soil type, vegetation type and coverage, land use, climate, and weathering/erosion rates.
    [Show full text]
  • Real-Time Stream Flow Gages in Montana
    REAL-TIME STREAM FLOW GAGES IN MONTANA Montana is home to over 264 real-time stream lows and improve water management practices. It gages located throughout the state. These gages can drive the understanding for other sciences and and their networks assist in delivering water data to helps inform citizens on how we can prepare for scientists and the public. While Montana’s demand changes in our water supply. It is imperative to for water continues to grow, water availability maintain as many gages as possible to preserve varies from year-to-year and can change these historical records for current and future dramatically in any given year. Managing supply and generations. demand challenges is an ongoing feature of life. REAL-TIME GAGES Accurate, near real-time, publicly accessible information on stream flows assists both day to day A real-time stream gage is used to report stream decision making and long-term planning, as well as flow (discharge) in cubic feet per second. These emergency planning and notification. This gages measure the stage (height) of the river in feet, information is generated in Montana by multiple and water temperature along with other networks of real-time stream gages operated by the environmental data. U.S. Geological Survey (USGS), the Department of Natural Resources and Conservation (DNRC), and some tribes. Within each network, the operation and maintenance of gages are financially supported by different sources including federal, state, tribal, local, and private funds. Some of the gages are funded by multiple agencies and organizations. The recorded data are essential to make informed water management decisions across the state.
    [Show full text]
  • Chapter 5 Streamflow Data
    Part 630 Hydrology National Engineering Handbook Chapter 5 Streamflow Data (210–VI–NEH, Amend. 76, November 2015) Chapter 5 Streamflow Data Part 630 National Engineering Handbook Issued November 2015 The U.S. Department of Agriculture (USDA) prohibits discrimination against its customers, em- ployees, and applicants for employment on the bases of race, color, national origin, age, disabil- ity, sex, gender identity, religion, reprisal, and where applicable, political beliefs, marital status, familial or parental status, sexual orientation, or all or part of an individual’s income is derived from any public assistance program, or protected genetic information in employment or in any program or activity conducted or funded by the Department. (Not all prohibited bases will apply to all programs and/or employment activities.) If you wish to file a Civil Rights program complaint of discrimination, complete the USDA Pro- gram Discrimination Complaint Form (PDF), found online at http://www.ascr.usda.gov/com- plaint_filing_cust.html, or at any USDA office, or call (866) 632-9992 to request the form. You may also write a letter containing all of the information requested in the form. Send your completed complaint form or letter to us by mail at U.S. Department of Agriculture, Director, Office of Adju- dication, 1400 Independence Avenue, S.W., Washington, D.C. 20250-9410, by fax (202) 690-7442 or email at [email protected] Individuals who are deaf, hard of hearing or have speech disabilities and you wish to file either an EEO or program complaint please contact USDA through the Federal Relay Service at (800) 877- 8339 or (800) 845-6136 (in Spanish).
    [Show full text]
  • Classifying Rivers - Three Stages of River Development
    Classifying Rivers - Three Stages of River Development River Characteristics - Sediment Transport - River Velocity - Terminology The illustrations below represent the 3 general classifications into which rivers are placed according to specific characteristics. These categories are: Youthful, Mature and Old Age. A Rejuvenated River, one with a gradient that is raised by the earth's movement, can be an old age river that returns to a Youthful State, and which repeats the cycle of stages once again. A brief overview of each stage of river development begins after the images. A list of pertinent vocabulary appears at the bottom of this document. You may wish to consult it so that you will be aware of terminology used in the descriptive text that follows. Characteristics found in the 3 Stages of River Development: L. Immoor 2006 Geoteach.com 1 Youthful River: Perhaps the most dynamic of all rivers is a Youthful River. Rafters seeking an exciting ride will surely gravitate towards a young river for their recreational thrills. Characteristically youthful rivers are found at higher elevations, in mountainous areas, where the slope of the land is steeper. Water that flows over such a landscape will flow very fast. Youthful rivers can be a tributary of a larger and older river, hundreds of miles away and, in fact, they may be close to the headwaters (the beginning) of that larger river. Upon observation of a Youthful River, here is what one might see: 1. The river flowing down a steep gradient (slope). 2. The channel is deeper than it is wide and V-shaped due to downcutting rather than lateral (side-to-side) erosion.
    [Show full text]
  • Stormwater Phase II Rule: Illicit Discharge Detection And
    United States Office of Water EPA 833-F-00-007 Environmental Protection (4203) January 2000 (revised December 2005) Agency Fact Sheet 2.5 Stormwater Phase II Final Rule Illicit Discharge Detection and Elimination Minimum Control Measure Stormwater Phase II his fact sheet profiles the Illicit Discharge Detection and Elimination minimum control Final Rule Tmeasure, one of six measures the operator of a Phase II regulated small municipal separate Fact Sheet Series storm sewer system (MS4) is required to include in its stormwater management program to meet the conditions of its National Pollutant Discharge Elimination System (NPDES) permit. This fact sheet outlines the Phase II Final Rule requirements and offers some general guidance Overview on how to satisfy them. It is important to keep in mind that the small MS4 operator has a great 1.0 – Stormwater Phase II Final deal of flexibility in choosing exactly how to satisfy the minimum control measure Rule: An Overview requirements. Small MS4 Program What Is An “Illicit Discharge”? 2.0 – Small MS4 Stormwater Program Overview ederal regulations define an illicit discharge Table 1 2.1 – Who’s Covered? Designation as “...any discharge to an MS4 that is not and Waivers of Regulated Small F MS4s composed entirely of stormwater...” with some Sources of exceptions. These exceptions include discharges Illicit Discharges 2.2 – Urbanized Areas: Definition and Description from NPDES-permitted industrial sources and discharges from fire-fighting activities. Illicit Sanitary wastewater discharges (see Table 1) are considered “illicit” Minimum Control Measures Effluent from septic tanks because MS4s are not designed to accept, process, 2.3 – Public Education and or discharge such non-stormwater wastes.
    [Show full text]
  • Hydrological Measurements
    Water Quality Monitoring - A Practical Guide to the Design and Implementation of Freshwater Quality Studies and Monitoring Programmes Edited by Jamie Bartram and Richard Ballance Published on behalf of United Nations Environment Programme and the World Health Organization © 1996 UNEP/WHO ISBN 0 419 22320 7 (Hbk) 0 419 21730 4 (Pbk) Chapter 12 - HYDROLOGICAL MEASUREMENTS This chapter was prepared by E. Kuusisto. Hydrological measurements are essential for the interpretation of water quality data and for water resource management. Variations in hydrological conditions have important effects on water quality. In rivers, such factors as the discharge (volume of water passing through a cross-section of the river in a unit of time), the velocity of flow, turbulence and depth will influence water quality. For example, the water in a stream that is in flood and experiencing extreme turbulence is likely to be of poorer quality than when the stream is flowing under quiescent conditions. This is clearly illustrated by the example of the hysteresis effect in river suspended sediments during storm events (see Figure 13.2). Discharge estimates are also essential when calculating pollutant fluxes, such as where rivers cross international boundaries or enter the sea. In lakes, the residence time (see section 2.1.1), depth and stratification are the main factors influencing water quality. A deep lake with a long residence time and a stratified water column is more likely to have anoxic conditions at the bottom than will a small lake with a short residence time and an unstratified water column. It is important that personnel engaged in hydrological or water quality measurements are familiar, in general terms, with the principles and techniques employed by each other.
    [Show full text]
  • A Look at the Links Between Drainage Density and Flood Statistics
    Hydrol. Earth Syst. Sci., 13, 1019–1029, 2009 www.hydrol-earth-syst-sci.net/13/1019/2009/ Hydrology and © Author(s) 2009. This work is distributed under Earth System the Creative Commons Attribution 3.0 License. Sciences A look at the links between drainage density and flood statistics B. Pallard1, A. Castellarin2, and A. Montanari2 1International Center for Agricultural Science and Natural resource Management Studies, Montpellier Supagro, Montpellier, France 2Faculty of Engineering, University of Bologna, Bologna, Italy Received: 28 August 2008 – Published in Hydrol. Earth Syst. Sci. Discuss.: 22 October 2008 Revised: 16 June 2009 – Accepted: 16 June 2009 – Published: 7 July 2009 Abstract. We investigate the links between the drainage den- Woodyer and Brookfield, 1966). Dd is also higher in highly sity of a river basin and selected flood statistics, namely, branched drainage basins with a relatively rapid hydrologic mean, standard deviation, coefficient of variation and coef- response (Melton, 1957). ficient of skewness of annual maximum series of peak flows. The drainage density exertes on flood peaks significant The investigation is carried out through a three-stage anal- controls which can be broadly divided between direct and ysis. First, a numerical simulation is performed by using a indirect effects (Merz and Bloschl¨ , 2008; Bloschl¨ , 2008). spatially distributed hydrological model in order to highlight Among the most significant direct effects there is the con- how flood statistics change with varying drainage density. trol associated with the length of the stream network and Second, a conceptual hydrological model is used in order hillslope paths. Because flow velocity is higher in the river to analytically derive the dependence of flood statistics on network, Dd significantly affects the concentration time and drainage density.
    [Show full text]
  • The Relationship Between Drainage Density and Soil Erosion Rate: a Study of Five Watersheds in Ardebil Province, Iran
    River Basin Management VIII 129 The relationship between drainage density and soil erosion rate: a study of five watersheds in Ardebil Province, Iran A. Moeini1, N. K. Zarandi1, E. Pazira1 & Y. Badiollahi2 1Department of Watershed Management, College of Agriculture and Natural Resources, Science and Research Branch, Islamic Azad University, Iran 2University College of Nabie Akram (UCNA), Iran Abstract Drainage density is one of the parameters that can be considered as an indicator of erosion rate. This study analysed the relationship between drainage density and soil erosion in five watersheds in Iran. The drainage density was measured using satellite images, aerial photos, and topographic maps by Geographic Information Systems (GIS) technologies. MPSIAC model was employed in a GIS environment to create soil erosion maps using data from meteorological stations, soil surveys, topographic maps, satellite images and results of other relevant studies. Then the correlation between drainage density and erosion rate was measured. The mean soil loss rate in the study areas were 1 to 6.43 t.h-1.y-1 and drainage density values varied 1.44 to 5.43 Km Km-1.The results indicate that the relationship between these two factors improved when the types of sheet erosion, mechanical erosion and mass erosion was ignored because these types of erosion were not mainly influenced by the power of runoff. There was a high correlation between drainage density and erosion in most of the watersheds. Finally a significant relationship was seen between drainage density and erosion in all watersheds. Based on the results obtained, the present method for distinguishing soil erosion was effective and can be used for operational erosion monitoring in other watersheds with the same climate characteristics in Iran.
    [Show full text]
  • Illicit Discharge and Stormwater Sewer Connection of Bannock County, Idaho Ordinance No
    #20925888 ILLICIT DISCHARGE AND STORMWATER SEWER CONNECTION OF BANNOCK COUNTY, IDAHO ORDINANCE NO. 6 SECTION 100 TITLE, PURPOSE AND INTENT: 110 TITLE : This ORDINANCE shall be known as the ILLICIT DISCHARGE AND STORMWATER SEWER CONNECTION ORDINANCE OF BANNOCK COUNTY, IDAHO. 110 STATUTORY AUTHORITY: The legislature of the State of Idaho in I.C. 31-714 authorized the Board of County Commissioners of Bannock County to pass ordinances to provide for the safety and promote the health and prosperity of the inhabitants of the county and to protect the property within the county. 120 STATEMENT OF PURPOSE: The purpose of this ordinance is to comply with the requirements of the county's national pollutant discharge elimination system (NPDES) permit no. IDS-028053, the federal clean water act, and to provide for the health, safety, and general welfare of the citizens of the county through the regulation of non-storm water discharges to the storm drainage system as required by federal and state law by establishing methods to control the introduction of pollutants into the municipal separate storm sewer system. The objectives of this ordinance are: A. To regulate the contribution of pollutants to the municipal separate storm sewer system (MS4) by stormwater discharges by any user. B. To prohibit illicit connections and discharges to the municipal separate storm sewer system. C. To establish legal authority to carry out all inspection, surveillance and monitoring procedures necessary to ensure compliance of this ordinance. D. To establish penalties associated with violations of this ordinance. SECTION 200 DEFINITIONS For the purposes of this ordinance, the following shall mean: AUTHORIZED ENFORCEMENT AGENT: The Bannock County Planning Director or the Bannock County Building Official or his designee.
    [Show full text]
  • Chapter 2 - WATER QUALITY
    Water Quality Monitoring - A Practical Guide to the Design and Implementation of Freshwater Quality Studies and Monitoring Programmes Edited by Jamie Bartram and Richard Ballance Published on behalf of United Nations Environment Programme and the World Health Organization © 1996 UNEP/WHO ISBN 0 419 22320 7 (Hbk) 0 419 21730 4 (Pbk) Chapter 2 - WATER QUALITY This chapter was prepared by M. Meybeck, E. Kuusisto, A. Mäkelä and E. Mälkki “Water quality” is a term used here to express the suitability of water to sustain various uses or processes. Any particular use will have certain requirements for the physical, chemical or biological characteristics of water; for example limits on the concentrations of toxic substances for drinking water use, or restrictions on temperature and pH ranges for water supporting invertebrate communities. Consequently, water quality can be defined by a range of variables which limit water use. Although many uses have some common requirements for certain variables, each use will have its own demands and influences on water quality. Quantity and quality demands of different users will not always be compatible, and the activities of one user may restrict the activities of another, either by demanding water of a quality outside the range required by the other user or by lowering quality during use of the water. Efforts to improve or maintain a certain water quality often compromise between the quality and quantity demands of different users. There is increasing recognition that natural ecosystems have a legitimate place in the consideration of options for water quality management. This is both for their intrinsic value and because they are sensitive indicators of changes or deterioration in overall water quality, providing a useful addition to physical, chemical and other information.
    [Show full text]
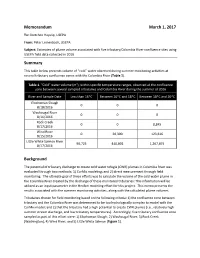
  • Estimates of Plume Volume Associated with Five Tributary/Columbia River Confluence Sites Using USEPA Field Data Collected in 2016
    Memorandum March 1, 2017 To: Gretchen Hayslip, USEPA From: Peter Leinenbach, USEPA Subject: Estimates of plume volume associated with five tributary/Columbia River confluence sites using USEPA field data collected in 2016 Summary This table below presents volume of “cold” water observed during summer monitoring activities at several tributary confluence zones with the Columbia River (Table 1). Table 1. “Cold” water volume (m3), within specific temperature ranges, observed at the confluence zone between several sampled tributaries and Columbia River during the summer of 2016 River and Sample Date Less than 16*C Between 16*C and 18*C Between 18*C and 20*C Elochoman Slough 0 0 0 8/18/2016 Washougal River 0 0 0 8/16/2016 Rock Creek 0 0 8,845 8/17/2016 Wind River 0 20,390 123,616 8/15/2016 Little White Salmon River 90,723 440,801 1,267,874 8/17/2016 Background The potential of tributary discharge to create cold water refugia (CWR) plumes in Columbia River was evaluated through two methods: 1) CorMix modeling; and 2) direct measurement through field monitoring. The ultimate goal of these efforts was to calculate the volume of the cold water plume in the Columbia River created by the discharge of these monitored tributaries: This information will be utilized as an input parameter in the HexSim modeling effort for this project. This memo presents the results associated with the summer monitoring activities, along with the calculated plume volumes. Tributaries chosen for field monitoring based on the following criteria: 1) the confluence zone between tributary and the Colombia River was determined to be too hydrologically complex to model with the CorMix model; and 2) that the tributary had a high potential to create CWR plumes (i.e., relatively high summer stream discharge, and low tributary temperatures).
    [Show full text]