DOCSLIB.ORG

Development and Preliminary Results of Point Source Observations

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Development and Preliminary Results of Point Source Observations The Atacama Cosmology Telescope: Development and Preliminary Results of Point Source Observations Ryan P. Fisher A DISSERTATION PRESENTED TO THE FACULTY OF PRINCETON UNIVERSITY IN CANDIDACY FOR THE DEGREE OF DOCTOR OF PHILOSOPHY RECOMMENDED FOR ACCEPTANCE BY THE DEPARTMENT OF PHYSICS [Adviser: Joseph W. Fowler] November 2009 c Copyright by Ryan Patrick Fisher, 2009. All rights reserved. Abstract The Atacama Cosmology Telescope (ACT) is a six meter diameter telescope designed to measure the millimeter sky with arcminute angular resolution. The instrument is cur- rently conducting its third season of observations from Cerro Toco in the Chilean Andes. The primary science goal of the experiment is to expand our understanding of cosmology by mapping the temperature fluctuations of the Cosmic Microwave Background (CMB) at angular scales corresponding to multipoles up to ` ∼ 10000: The primary receiver for current ACT observations is the Millimeter Bolometer Ar- ray Camera (MBAC). The instrument is specially designed to observe simultaneously at 148 GHz, 218 GHz and 277 GHz. To accomplish this, the camera has three separate de- tector arrays, each containing approximately 1000 detectors. After discussing the ACT experiment in detail, a discussion of the development and testing of the cold readout elec- tronics for the MBAC is presented. Currently, the ACT collaboration is in the process of generating maps of the microwave sky using our first and second season observations. The analysis used to generate these maps requires careful data calibration to produce maps of the arcminute scale CMB tem- perature fluctuations. Tests and applications of several elements of the ACT calibrations are presented in the context of the second season observations. Scientific exploration has already begun on preliminary maps made using these calibrations. The final portion of this thesis is dedicated to discussing the point sources observed by the ACT. A discus- sion of the techniques used for point source detection and photometry is followed by a presentation of our current measurements of point source spectral indices. iii Acknowledgments I am very grateful for the opportunities I have had to learn and grow as a researcher thanks to Princeton University. The atmosphere of excitement for discovery in the Physics Department is like nothing I have ever experienced before. Through my years of gradu- ate work, I have been guided and supported by Lyman Page, Suzanne Staggs, and my advisor, Joseph Fowler. I truly appreciate having the opportunity to study under such a brilliant trio of scientists. I especially would like to thank Joe for helping me through my years of graduate work and for spending countless hours having discussions with me on topics ranging from cosmology to coffee. I owe very much of this thesis to the work of so many other individuals. I have been lucky to both follow in the footsteps of many great scientists who have come before me, and walk the path with the most excellent of peers one could wish for. In particular, I have had the pleasure of working with and learning from the many members who have been a part of the ACT collaboration including: Mike Niemack, Judy Lau, Toby Marriage, Asad Aboobaker, Yue Zhao, Tom Essinger-Hileman, John Appel, Lucas Parker, Sudeep Das, Amir Hajian, Viviana Acquaviva, Beth Reid, Kevin Huffenburger, Elia Battistelli, Rolondo Du¨nner, Matt Hasselfield, Mike Nolta, Jon Sievers, Neelima Sehgal, Matt Hilton, Jo Dunk- ley, Norm Jarosik, Kavi Moodley, David Spergel, Omelan Stryzak, Daniel Swetz, Danica Marsden, Krista Martocci, Alex Dahlen, Leizhi Sun, Sarah Denny, Mark Halpern, Jeff Klein, Michele Limon, Robert Lupton, Randy Doriese, Gene Hilton, Jay Chervenak, Ryan Warne and Audrey Sederberg, to name but a few. I would like to thank all of the staff of the Physics Department, and especially those who are always so friendly and helpful to me: Barbara Grunwerg, Claude Champagne, Mary Santay, Laurel Lerner, Angela Glenn, John Washington and Mike Peloso. I would also like to particularly thank the members of the machine shop lunch crew, Glenn, Bill, Ray, and occasionally Bob Austin, who have shared many an excellent conversation with me. I would like to especially thank the two individuals who have shared far more than just an office with me over the last few years, Eric Switzer and Adam Hincks, for their camaraderie, help and friendship. My years at Princeton have gifted me with so many friends, including many whom I have already acknowledged as peers. I could hardly imagine listing the countless number of individuals who have brought an ounce of happiness to my time at Princeton, but I would like to point out a few individuals who have been truly good friends. First, I would like to thank the basement crew of Justin Brown, Rajat Ghosh, Scott Seltzer, Hoan Dang, and Giorgos Vasilakis, for providing me with both friendship and entertainment on the many occasions when I required it. Next I would like to thank Omelan Stryzak and Ted Lewis for always providing me with the help I needed, but more importantly by far for their friendships extending beyond the walls and topics of Jadwin Hall. Finally, I would like to thank Sam Taylor, Lewis Andrew Wray, Nick Pavlov and Jeremy Booher for all of the fun times we’ve spent together. To Nick and Justin and Jeremy, thanks for all of the laughter you have brought into my life all these years. To all of my friends: I will miss you dearly iv when I move on, and I hope that our paths will cross again. I owe so very much to the love and support of my parents, Jackie and Gary Fisher. Thank you both for helping me through everything that I have done. Throughout my years of study, I have always had the love of my life by my side. She has always helped me through my greatest times of need and given me a reason to be happy every day. My greatest thanks go to you, Julie, I love you, and I dedicate this thesis to you and our future together. v vi Contents Abstract......................................... iii Acknowledgments................................... iv List of Figures.....................................x List of Tables...................................... xiii 1 Cosmology, the CMB, and the Atacama Cosmology Telescope1 1.1 The CMB.....................................3 1.2 Primary Anisotropies of the CMB........................5 1.3 Secondary Effects................................ 11 1.4 Millimeter Astronomy............................... 13 1.5 The ACT Experiment............................... 14 1.5.1 ACT Observations............................ 16 1.6 Outline of Thesis................................. 17 2 The ACT Telescope Systems Overview 19 2.1 Telescope Infrastructure............................. 20 2.1.1 Measurements of the Telescope Beam................. 24 2.2 The MBAC.................................... 26 2.2.1 ACT Cold Optics and Bandpasses................... 26 2.2.2 Detector Arrays.............................. 26 2.2.3 Detector Circuitry............................. 31 2.2.4 Cold Readout Electronics........................ 35 2.3 Receiver Cabin Electronics........................... 40 2.3.1 The MCE Readout System....................... 41 2.3.2 Data Modes in the MCE......................... 41 2.4 Data Readout Computers............................ 45 2.5 Data........................................ 46 3 Tests of Multiplexing Electronics for the Atacama Cosmology Telescope 49 3.1 Mux Chip Testing Experimental Setup..................... 50 3.2 IcMax Characterization.............................. 54 3.2.1 Selection Criteria............................. 54 3.2.2 Analysis of Desired Biasing Currents.................. 56 3.2.3 Wafer Characterization......................... 61 3.2.4 Anticipated Requirements for Mux Chips................ 63 vii 3.3 Advancements in Mux Chip Production and Screening After the Initial Study 65 3.4 Automated Testing of Mux Chip Assemblies.................. 65 3.5 Aggregate Testing Results............................ 67 3.6 Final Array Chip Performance.......................... 69 4 ACT Calibration for 2008 71 4.1 Detector and Readout Circuit Formalism.................... 72 4.2 The Load Curve Test............................... 79 4.2.1 2008 AR1 IV Curve Problem and Solution............... 83 4.3 The Bias Step Test................................ 85 4.3.1 Analysis of Bias Step Test Files..................... 88 4.3.2 Tests of the Analysis Code....................... 91 4.3.3 Comparisons of IV Curve and Bias Step Tests............ 103 4.4 Atmospheric Flat Fielding Calibration...................... 109 4.4.1 Concept.................................. 109 4.4.2 Implementation.............................. 112 4.4.3 Detailed Description of AR3 Difficulties................ 117 4.5 Efficiency Computations............................. 118 4.6 Final Calibration Method and Results...................... 122 4.6.1 Absolute Calibration to Uranus..................... 131 4.6.2 Conclusion................................ 132 5 Point Sources in the ACT Survey 133 5.1 Point Source Types................................ 134 5.1.1 Radio Source Radiation Mechanism.................. 134 5.1.2 IR Source Radiation........................... 137 5.2 Project Motivation and Goals.......................... 139 5.2.1 Spectral Indices............................. 139 5.2.2 Source Characteristics.......................... 140 5.2.3 Cluster Observations.......................... 140 5.2.4 Additional Motivations.......................... 141 5.2.5 Goals of This Research........................
Load more

Recommended publications
  • Detection of Polarization in the Cosmic Microwave Background Using DASI
    Detection of Polarization in the Cosmic Microwave Background using DASI Thesis by John M. Kovac A Dissertation Submitted to the Faculty of the Division of the Physical Sciences in Candidacy for the Degree of Doctor of Philosophy The University of Chicago Chicago, Illinois 2003 Copyright c 2003 by John M. Kovac ° (Defended August 4, 2003) All rights reserved Acknowledgements Abstract This is a sample acknowledgement section. I would like to take this opportunity to The past several years have seen the emergence of a new standard cosmological model thank everyone who contributed to this thesis. in which small temperature di®erences in the cosmic microwave background (CMB) I would like to take this opportunity to thank everyone. I would like to take on degree angular scales are understood to arise from acoustic oscillations in the hot this opportunity to thank everyone. I would like to take this opportunity to thank plasma of the early universe, sourced by primordial adiabatic density fluctuations. In everyone. the context of this model, recent measurements of the temperature fluctuations have led to profound conclusions about the origin, evolution and composition of the uni- verse. Given knowledge of the temperature angular power spectrum, this theoretical framework yields a prediction for the level of the CMB polarization with essentially no free parameters. A determination of the CMB polarization would therefore provide a critical test of the underlying theoretical framework of this standard model. In this thesis, we report the detection of polarized anisotropy in the Cosmic Mi- crowave Background radiation with the Degree Angular Scale Interferometer (DASI), located at the Amundsen-Scott South Pole research station.
    [Show full text]
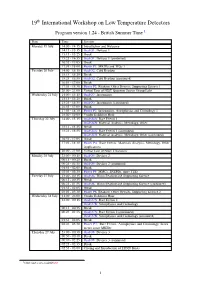
  • 19 International Workshop on Low Temperature Detectors
    19th International Workshop on Low Temperature Detectors Program version 1.24 - British Summer Time 1 Date Time Session Monday 19 July 14:00 - 14:15 Introduction and Welcome 14:15 - 15:15 Oral O1: Devices 1 15:15 - 15:25 Break 15:25 - 16:55 Oral O1: Devices 1 (continued) 16:55 - 17:05 Break 17:05 - 18:00 Poster P1: MKIDs and TESs 1 Tuesday 20 July 14:00 - 15:15 Oral O2: Cold Readout 15:15 - 15:25 Break 15:25 - 16:55 Oral O2: Cold Readout (continued) 16:55 - 17:05 Break 17:05 - 18:30 Poster P2: Readout, Other Devices, Supporting Science 1 20:00 - 21:00 Virtual Tour of NIST Quantum Sensor Group Labs Wednesday 21 July 14:00 - 15:15 Oral O3: Instruments 15:15 - 15:25 Break 15:25 - 16:55 Oral O3: Instruments (continued) 16:55 - 17:05 Break 17:05 - 18:30 Poster P3: Instruments, Astrophysics and Cosmology 1 18:00 - 19:00 Vendor Exhibitor Hour Thursday 22 July 14:00 - 15:15 Oral O4A: Rare Events 1 Oral O4B: Material Analysis, Metrology, Other 15:15 - 15:25 Break 15:25 - 16:55 Oral O4A: Rare Events 1 (continued) Oral O4B: Material Analysis, Metrology, Other (continued) 16:55 - 17:05 Break 17:05 - 18:30 Poster P4: Rare Events, Materials Analysis, Metrology, Other Applications 20:00 - 21:00 Virtual Tour of NIST Cleanoom Monday 26 July 23:00 - 00:15 Oral O5: Devices 2 00:15 - 00:25 Break 00:25 - 01:55 Oral O5: Devices 2 (continued) 01:55 - 02:05 Break 02:05 - 03:30 Poster P5: MMCs, SNSPDs, more TESs Tuesday 27 July 23:00 - 00:15 Oral O6: Warm Readout and Supporting Science 00:15 - 00:25 Break 00:25 - 01:55 Oral O6: Warm Readout and Supporting Science
    [Show full text]
  • CMB Telescopes and Optical Systems to Appear In: Planets, Stars and Stellar Systems (PSSS) Volume 1: Telescopes and Instrumentation
    CMB Telescopes and Optical Systems To appear in: Planets, Stars and Stellar Systems (PSSS) Volume 1: Telescopes and Instrumentation Shaul Hanany ([email protected]) University of Minnesota, School of Physics and Astronomy, Minneapolis, MN, USA, Michael Niemack ([email protected]) National Institute of Standards and Technology and University of Colorado, Boulder, CO, USA, and Lyman Page ([email protected]) Princeton University, Department of Physics, Princeton NJ, USA. March 26, 2012 Abstract The cosmic microwave background radiation (CMB) is now firmly established as a funda- mental and essential probe of the geometry, constituents, and birth of the Universe. The CMB is a potent observable because it can be measured with precision and accuracy. Just as importantly, theoretical models of the Universe can predict the characteristics of the CMB to high accuracy, and those predictions can be directly compared to observations. There are multiple aspects associated with making a precise measurement. In this review, we focus on optical components for the instrumentation used to measure the CMB polarization and temperature anisotropy. We begin with an overview of general considerations for CMB ob- servations and discuss common concepts used in the community. We next consider a variety of alternatives available for a designer of a CMB telescope. Our discussion is guided by arXiv:1206.2402v1 [astro-ph.IM] 11 Jun 2012 the ground and balloon-based instruments that have been implemented over the years. In the same vein, we compare the arc-minute resolution Atacama Cosmology Telescope (ACT) and the South Pole Telescope (SPT). CMB interferometers are presented briefly. We con- clude with a comparison of the four CMB satellites, Relikt, COBE, WMAP, and Planck, to demonstrate a remarkable evolution in design, sensitivity, resolution, and complexity over the past thirty years.
    [Show full text]
  • From Current Cmbology to Its Polarization and SZ Frontiers Circa TAW8 3
    AMiBA 2001: High-z Clusters, Missing Baryons, and CMB Polarization ASP Conference Series, Vol. 999, 2002 L-W Chen, C-P Ma, K-W Ng and U-L Pen, eds Concluding Remarks: From Current CMBology to its Polarization and Sunyaev-Zeldovich Frontiers circa TAW8 J. Richard Bond Canadian Institute for Theoretical Astrophysics, University of Toronto, Toronto, Ontario, M5S 3H8, Canada Abstract. I highlight the remarkable advances in the past few years in CMB research on total primary anisotropies, in determining the power spectrum, deriving cosmological parameters from it, and more generally lending credence to the basic inflation-based paradigm for cosmic struc- ture formation, with a flat geometry, substantial dark matter and dark energy, baryonic density in good accord with that from nucleosynthe- sis, and a nearly scale invariant initial fluctuation spectrum. Some pa- rameters are nearly degenerate with others and CMB polarization and many non-CMB probes are needed to determine them, even within the paradigm. Such probes and their tools were the theme of the TAW8 meeting: our grand future of CMB polarization, with AMiBA, ACBAR, B2K2, CBI, COMPASS, CUPMAP, DASI, MAP, MAXIPOL, PIQUE, Planck, POLAR, Polatron, QUEST, Sport/BaRSport, and of Sunyaev- Zeldovich experiments, also using an array of platforms and detectors, e.g., AMiBA, AMI (Ryle+), CBI, CARMA (OVROmm+BIMA), MINT, SZA, BOLOCAM+CSO, LMT, ACT. The SZ probe will be informed and augmented by new ambitious attacks on other cluster-system observables discussed at TAW8: X-ray, optical, weak lensing. Interpreting the mix is complicated by such issues as entropy injection, inhomogeneity, non- sphericity, non-equilibrium, and these effects must be sorted out for the cluster system to contribute to “high precision cosmology”, especially the quintessential physics of the dark energy that adds further mystery to a dark matter dominated Universe.
    [Show full text]
  • The Design of the Ali CMB Polarization Telescope Receiver
    The design of the Ali CMB Polarization Telescope receiver M. Salatinoa,b, J.E. Austermannc, K.L. Thompsona,b, P.A.R. Aded, X. Baia,b, J.A. Beallc, D.T. Beckerc, Y. Caie, Z. Changf, D. Cheng, P. Chenh, J. Connorsc,i, J. Delabrouillej,k,e, B. Doberc, S.M. Duffc, G. Gaof, S. Ghoshe, R.C. Givhana,b, G.C. Hiltonc, B. Hul, J. Hubmayrc, E.D. Karpela,b, C.-L. Kuoa,b, H. Lif, M. Lie, S.-Y. Lif, X. Lif, Y. Lif, M. Linkc, H. Liuf,m, L. Liug, Y. Liuf, F. Luf, X. Luf, T. Lukasc, J.A.B. Matesc, J. Mathewsonn, P. Mauskopfn, J. Meinken, J.A. Montana-Lopeza,b, J. Mooren, J. Shif, A.K. Sinclairn, R. Stephensonn, W. Sunh, Y.-H. Tsengh, C. Tuckerd, J.N. Ullomc, L.R. Valec, J. van Lanenc, M.R. Vissersc, S. Walkerc,i, B. Wange, G. Wangf, J. Wango, E. Weeksn, D. Wuf, Y.-H. Wua,b, J. Xial, H. Xuf, J. Yaoo, Y. Yaog, K.W. Yoona,b, B. Yueg, H. Zhaif, A. Zhangf, Laiyu Zhangf, Le Zhango,p, P. Zhango, T. Zhangf, Xinmin Zhangf, Yifei Zhangf, Yongjie Zhangf, G.-B. Zhaog, and W. Zhaoe aStanford University, Stanford, CA 94305, USA bKavli Institute for Particle Astrophysics and Cosmology, Stanford, CA 94305, USA cNational Institute of Standards and Technology, Boulder, CO 80305, USA dCardiff University, Cardiff CF24 3AA, United Kingdom eUniversity of Science and Technology of China, Hefei 230026 fInstitute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049 gNational Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012 hNational Taiwan University, Taipei 10617 iUniversity of Colorado Boulder, Boulder, CO 80309, USA jIN2P3, CNRS, Laboratoire APC, Universit´ede Paris, 75013 Paris, France kIRFU, CEA, Universit´eParis-Saclay, 91191 Gif-sur-Yvette, France lBeijing Normal University, Beijing 100875 mAnhui University, Hefei 230039 nArizona State University, Tempe, AZ 85004, USA oShanghai Jiao Tong University, Shanghai 200240 pSun Yat-Sen University, Zhuhai 519082 ABSTRACT Ali CMB Polarization Telescope (AliCPT-1) is the first CMB degree-scale polarimeter to be deployed on the Tibetan plateau at 5,250 m above sea level.
    [Show full text]
  • Clover: Measuring Gravitational-Waves from Inflation
    ClOVER: Measuring gravitational-waves from Inflation Executive Summary The existence of primordial gravitational waves in the Universe is a fundamental prediction of the inflationary cosmological paradigm, and determination of the level of this tensor contribution to primordial fluctuations is a uniquely powerful test of inflationary models. We propose an experiment called ClOVER (ClObserVER) to measure this tensor contribution via its effect on the geometric properties (the so-called B-mode) of the polarization of the Cosmic Microwave Background (CMB) down to a sensitivity limited by the foreground contamination due to lensing. In order to achieve this sensitivity ClOVER is designed with an unprecedented degree of systematic control, and will be deployed in Antarctica. The experiment will consist of three independent telescopes, operating at 90, 150 or 220 GHz respectively, and each of which consists of four separate optical assemblies feeding feedhorn arrays arrays of superconducting detectors with phase as well as intensity modulation allowing the measurement of all three Stokes parameters I, Q and U in every pixel. This project is a combination of the extensive technical expertise and experience of CMB measurements in the Cardiff Instrumentation Group (Gear) and Cavendish Astrophysics Group (Lasenby) in UK, the Rome “La Sapienza” (de Bernardis and Masi) and Milan “Bicocca” (Sironi) CMB groups in Italy, and the Paris College de France Cosmology group (Giraud-Heraud) in France. This document is based on the proposal submitted to PPARC by the UK groups (and funded with 4.6ML), integrated with additional information on the Dome-C site selected for the operations. This document has been prepared to obtain an endorsement from the INAF (Istituto Nazionale di Astrofisica) on the scientific quality of the proposed experiment to be operated in the Italian-French base of Dome-C, and to be submitted to the Commissione Scientifica Nazionale Antartica and to the French INSU and IPEV.
    [Show full text]
  • Extrapolation of Galactic Dust Emission at 100 Microns to Cosmic Microwave Background Radiation Frequencies Using FIRAS
    Extrapolation of Galactic Dust Emission at 100 Microns to Cosmic Microwave Background Radiation Frequencies Using FIRAS The Harvard community has made this article openly available. Please share how this access benefits you. Your story matters Citation Finkbeiner, Douglas P., Marc Davis, and David J. Schlegel. 1999. “Extrapolation of Galactic Dust Emission at 100 Microns to Cosmic Microwave Background Radiation Frequencies Using FIRAS.” The Astrophysical Journal 524 (2) (October 20): 867–886. doi:10.1086/307852. Published Version 10.1086/307852 Citable link http://nrs.harvard.edu/urn-3:HUL.InstRepos:33462888 Terms of Use This article was downloaded from Harvard University’s DASH repository, and is made available under the terms and conditions applicable to Other Posted Material, as set forth at http:// nrs.harvard.edu/urn-3:HUL.InstRepos:dash.current.terms-of- use#LAA THE ASTROPHYSICAL JOURNAL, 524:867È886, 1999 October 20 ( 1999. The American Astronomical Society. All rights reserved. Printed in U.S.A. EXTRAPOLATION OF GALACTIC DUST EMISSION AT 100 MICRONS TO COSMIC MICROWAVE BACKGROUND RADIATION FREQUENCIES USING FIRAS DOUGLAS P. FINKBEINER AND MARC DAVIS University of California at Berkeley, Departments of Physics and Astronomy, 601 Campbell Hall, Berkeley, CA 94720; dÐnk=astro.berkeley.edu, marc=deep.berkeley.edu AND DAVID J. SCHLEGEL Princeton University, Department of Astrophysics, Peyton Hall, Princeton, NJ 08544; schlegel=astro.princeton.edu Received 1999 March 5; accepted 1999 June 8 ABSTRACT We present predicted full-sky maps of submillimeter and microwave emission from the di†use inter- stellar dust in the Galaxy. These maps are extrapolated from the 100 km emission and 100/240 km Ñux ratio maps that Schlegel, Finkbeiner, & Davis generated from IRAS and COBE/DIRBE data.
    [Show full text]
  • The Cℓover Experiment
    Invited Paper The CℓOVER Experiment L. Piccirillo1, P. Ade2, M. D. Audley3, C. Baines1, R. Battye1, M. Brown3, P. Calisse2, A. Challinor5,6, W. D. Duncan7, P. Ferreira4, W. Gear2, D. M. Glowacka3, D. Goldie3, P.K. Grimes4, M. Halpern8, V. Haynes1, G. C. Hilton7, K. D. Irwin7, B. Johnson4, M. Jones4, A. Lasenby3, P. Leahy1, J. Leech4, S. Lewis1, B. Maffei1, L. Martinis1, P. D. Mauskopf2, S. J. Melhuish1, C. E. North4, D. O'Dea3, S. Parsley2, G. Pisano1, C. D. Reintsema7, G. Savini2, R.V. Sudiwala2, D. Sutton4, A. Taylor4, G. Teleberg2, D. Titterington3, V. N. Tsaneva3, C. Tucker2, R. Watson1, S. Withington3, G. Yassin4, J. Zhang2 1 School of Physics and Astronomy, University of Manchester, UK 2 School of Physics and Astronomy, Cardiff University, UK 3 Cavendish Laboratory, University of Cambridge, Cambridge, UK 4 Astrophysics, University of Oxford, Oxford, UK 5 Institute of Astronomy, University of Cambridge, Cambridge, UK 6 DAMTP, University of Cambridge, Cambridge, UK 7 National Institute of Standards and Technology, USA 8 University of British Columbia, Canada CℓOVER is a multi-frequency experiment optimised to measure the Cosmic Microwave Background (CMB) polarization, in particular the B- mode component. CℓOVER comprises two instruments observing respectively at 97 GHz and 150/225 GHz. The focal plane of both instruments consists of an array of corrugated feed-horns coupled to TES detectors cooled at 100 mK. The primary science goal of CℓOVER is to be sensitive to gravitational waves down to r ~ 0.03 (at 3σ) in two years of operations. 1 Introduction The Cosmic Microwave Background (CMB) Radiation is a very powerful tool to study the origin and evolution of the Universe.
    [Show full text]
  • A Fast Iterative Multi-Grid Map-Making Algorithm for CMB Experiments
    A&A 374, 358–370 (2001) Astronomy DOI: 10.1051/0004-6361:20010692 & c ESO 2001 Astrophysics MAPCUMBA: A fast iterative multi-grid map-making algorithm for CMB experiments O. Dor´e1,R.Teyssier1,2,F.R.Bouchet1,D.Vibert1, and S. Prunet3 1 Institut d’Astrophysique de Paris, 98bis, Boulevard Arago, 75014 Paris, France 2 Service d’Astrophysique, DAPNIA, Centre d’Etudes´ de Saclay, 91191 Gif-sur-Yvette, France 3 CITA, McLennan Labs, 60 St George Street, Toronto, ON M5S 3H8, Canada Received 21 December 2000 / Accepted 2 May 2001 Abstract. The data analysis of current Cosmic Microwave Background (CMB) experiments like BOOMERanG or MAXIMA poses severe challenges which already stretch the limits of current (super-) computer capabilities, if brute force methods are used. In this paper we present a practical solution for the optimal map making problem which can be used directly for next generation CMB experiments like ARCHEOPS and TopHat, and can probably be extended relatively easily to the full PLANCK case. This solution is based on an iterative multi-grid Jacobi algorithm which is both fast and memory sparing. Indeed, if there are Ntod data points along the one dimensional timeline to analyse, the number of operations is of O(Ntod ln Ntod) and the memory requirement is O(Ntod). Timing and accuracy issues have been analysed on simulated ARCHEOPS and TopHat data, and we discuss as well the issue of the joint evaluation of the signal and noise statistical properties. Key words. methods: data analysis – cosmic microwave background 1. Introduction in this massive computing approach, i.e.
    [Show full text]
  • Mid-Infrared Selection of Brown Dwarfs and High-Redshift Quasars
    Submitted to the Astrophysical Journal Mid-Infrared Selection of Brown Dwarfs and High-Redshift Quasars Daniel Stern1, J. Davy Kirkpatrick2, Lori E. Allen3, Chao Bian4, Andrew Blain4, Kate Brand5, Mark Brodwin1, Michael J. I. Brown6, Richard Cool7, Vandana Desai4, Arjun Dey8, Peter Eisenhardt1, Anthony Gonzalez9, Buell T. Jannuzi8, Karin Menendez-Delmestre4, Howard A. Smith3, B. T. Soifer4,10, Glenn P. Tiede11 & E. Wright12 ABSTRACT We discuss color selection of rare objects in a wide-field, multiband survey span- ning from the optical to the mid-infrared. Simple color criteria simultaneously identify and distinguish two of the most sought after astrophysical sources: the coolest brown dwarfs and the most distant quasars. We present spectroscopically-confirmed examples of each class identified in the IRAC Shallow Survey of the Bo¨otes field of the NOAO Deep Wide-Field Survey. ISS J142950.9+333012 is a T4.5 brown dwarf at a distance of approximately 42 pc, and ISS J142738.5+331242 is a radio-loud quasar at redshift z = 6.12. Our selection criteria identify a total of four candidates over 8 square degrees of the Bo¨otes field. The other two candidates are both confirmed 5.5 <z< 6 quasars, previously reported by Cool et al. (2006). We discuss the implications of these dis- coveries and conclude that there are excellent prospects for extending such searches to cooler brown dwarfs and higher redshift quasars. 1Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Dr., Mail Stop 169-506, Pasadena, CA 91109 [e-mail: [email protected]]
    [Show full text]
  • A Bit of History Satellites Balloons Ground-Based
    Experimental Landscape ● A Bit of History ● Satellites ● Balloons ● Ground-Based Ground-Based Experiments There have been many: ABS, ACBAR, ACME, ACT, AMI, AMiBA, APEX, ATCA, BEAST, BICEP[2|3]/Keck, BIMA, CAPMAP, CAT, CBI, CLASS, COBRA, COSMOSOMAS, DASI, MAT, MUSTANG, OVRO, Penzias & Wilson, etc., PIQUE, Polatron, Polarbear, Python, QUaD, QUBIC, QUIET, QUIJOTE, Saskatoon, SP94, SPT, SuZIE, SZA, Tenerife, VSA, White Dish & more! QUAD 2017-11-17 Ganga/Experimental Landscape 2/33 Balloons There have been a number: 19 GHz Survey, Archeops, ARGO, ARCADE, BOOMERanG, EBEX, FIRS, MAX, MAXIMA, MSAM, PIPER, QMAP, Spider, TopHat, & more! BOOMERANG 2017-11-17 Ganga/Experimental Landscape 3/33 Satellites There have been 4 (or 5?): Relikt, COBE, WMAP, Planck (+IRTS!) Planck 2017-11-17 Ganga/Experimental Landscape 4/33 Rockets & Airplanes For example, COBRA, Berkeley-Nagoya Excess, U2 Anisotropy Measurements & others... It’s difficult to get integration time on these platforms, so while they are still used in the infrared, they are no longer often used for the http://aether.lbl.gov/www/projects/U2/ CMB. 2017-11-17 Ganga/Experimental Landscape 5/33 (from R. Stompor) Radek Stompor http://litebird.jp/eng/ 2017-11-17 Ganga/Experimental Landscape 6/33 Other Satellite Possibilities ● US “CMB Probe” ● CORE-like – Studying two possibilities – Discussions ongoing ● Imager with India/ISRO & others ● Spectrophotometer – Could include imager – Inputs being prepared for AND low-angular- the Decadal Process resolution spectrophotometer? https://zzz.physics.umn.edu/ipsig/
    [Show full text]
  • Imagine the Universe News - 1 March 2001 3/7/01 6:40 PM
    Imagine the Universe News - 1 March 2001 3/7/01 6:40 PM ˚enter search text ____________________________________________________________________________________________ Imaginemagine the Universe News Thee Latest on the Structure and Evolution of Our Universe For More ____________________________________________________________________________________________ Information... Vol 5. No. 4 1 March 2001 Classyassy Antarctic Balloon Learn more Capturesr es the Earliest Light of about the Universe electromagnetic radiation. McMurdo Station,n, Antarctica -- If you think penguins in Antarctica look classy in their tuxedos, you shoulduld see our scientific balloon wearing a top hat. Read questions and answers about cosmology. Visit the TopHat, an innovativevative hat-shaped TopHat site! astronomy experimentriment that sits on top of a balloon, circled around the frozen continent Antarctic at 120,000 feet foror nearly two weeks in Experiments for Beginning January, collectingng light from the cosmic Scientists microwave backgroundgroundradiation . The flight was a success, and TopHat scientists are noww back in the relative warmth of the Unitednited States, beginning the News Archive yearlong processs of analyzing the data. Observing the microwaveicrowave background, formed about 300,0000,000 years after the big bang, enables scientistsientists to understand the nature of our Universeiverse when it was an infant. The radiationtion comes from an era before the creationon of stars andgalaxies . The Universe is now about 10 to 15 billion TopHat Launch years old. Click for larger image. "It is remarkable that we can determine so much with such data," said Stephan Meyer, a TopHat scientist at the University of Chicago. "For instance, we can measure the mass of the Universe to about 10 percent accuracy. The data will also help to establish whether the Universe will expand forever, or eventually collapse upon itself." TopHat measures the clumpiness of matter when the Universe was very young.
    [Show full text]