DOCSLIB.ORG

Clover: Measuring Gravitational-Waves from Inflation

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Clover: Measuring Gravitational-Waves from Inflation ClOVER: Measuring gravitational-waves from Inflation Executive Summary The existence of primordial gravitational waves in the Universe is a fundamental prediction of the inflationary cosmological paradigm, and determination of the level of this tensor contribution to primordial fluctuations is a uniquely powerful test of inflationary models. We propose an experiment called ClOVER (ClObserVER) to measure this tensor contribution via its effect on the geometric properties (the so-called B-mode) of the polarization of the Cosmic Microwave Background (CMB) down to a sensitivity limited by the foreground contamination due to lensing. In order to achieve this sensitivity ClOVER is designed with an unprecedented degree of systematic control, and will be deployed in Antarctica. The experiment will consist of three independent telescopes, operating at 90, 150 or 220 GHz respectively, and each of which consists of four separate optical assemblies feeding feedhorn arrays arrays of superconducting detectors with phase as well as intensity modulation allowing the measurement of all three Stokes parameters I, Q and U in every pixel. This project is a combination of the extensive technical expertise and experience of CMB measurements in the Cardiff Instrumentation Group (Gear) and Cavendish Astrophysics Group (Lasenby) in UK, the Rome “La Sapienza” (de Bernardis and Masi) and Milan “Bicocca” (Sironi) CMB groups in Italy, and the Paris College de France Cosmology group (Giraud-Heraud) in France. This document is based on the proposal submitted to PPARC by the UK groups (and funded with 4.6ML), integrated with additional information on the Dome-C site selected for the operations. This document has been prepared to obtain an endorsement from the INAF (Istituto Nazionale di Astrofisica) on the scientific quality of the proposed experiment to be operated in the Italian-French base of Dome-C, and to be submitted to the Commissione Scientifica Nazionale Antartica and to the French INSU and IPEV. 1 Index 1: Scientific Objective 3 1.1: Cosmic microwave background polarization observables 1.2: Current status of cosmic microwave background polarimetry 1.3 The scientific case for CLOVER 1.4: Foregrounds 1.5: Other Polarization Experiments 2: Technical specification 21 2.1: Overview of the experiment 2.2: Detailed description of key areas 2.2.1: Telescope and mount 2.2.2: Cryogenics 2.2.3: Array and polarimeter 2.3.3: Horns 2.3.4: Orthomode transducers (OMTs) 2.3.5: Waveguide hybrids 2.3.6: Phase shifters 2.3.7: Waveguide twists, transitions and bends 2.3.8: Superconducting detector array 2.4: Systematics 2.5: Scanning strategy 2.6: Site and Logistics 3: New technologies 41 4: Implementation of ClOVER/BRAIN at Dome-C 41 4.1: Introduction 4.2: Buidings/Construction 4.3: Electrical 4.4: Data Storage 4.5: Calibration 4.6: Timing and Personnel 5: Costs to UK 44 6: Costs to Italy and France 44 7: Draft Memorandum of Understanding between UK, France, Italy 45 2 1: Scientific objective 1.1: Cosmic microwave background polarization observables Thomson scattering of anisotropic radiation at last scattering gives rise to linear polarization in the cosmic microwave background (Rees 1968). The polarization signal is expected to have an r.m.s. ~5 mK, peaking at multipoles l~1000, corresponding to the angle ( q~p/l ) subtended by the photon mean free path at last scattering. The polarization signal depends sensitively on the fluctuations on the last scattering surface, and thus encodes a wealth of cosmological information, complementary to that contained in the temperature anisotropies. In addition, large-angle polarization is generated by subsequent re-scattering as the universe reionizes, providing a unique probe of the ionization history at high redshift. Linear polarization, characterised by Stokes parameters Q and U, can be decomposed into a curl-free part (electric; denoted E) and a divergence-free part (magnetic or B; Seljak & Zaldarriaga 1997; Kamionkowski, Kosowsky & Stebbins 1997). The electric and magnetic parts can be represented by their spherical multipoles on the full sky, Elm and Blm, which are related to the Stokes parameters by a spin-2 spherical harmonic expansion: r m r (Q ± iU )(n) = å(Elm m Blm )m2 Yl (n) l,m Under the assumption of statistical isotropy, different l and m modes are uncorrelated, and the * E polarization power spectra are defined by e.g. Elm Elm = Cl . The cross-correlation between E and B vanishes if parity invariance holds in the mean. Rotationally- and parity-invariant T E B theories thus predict four non-vanishing power spectra, C l , C l , C l and the cross-correlation of TE E and T, the temperature anisotropies, Cl . Examples of pure electric and magnetic polarization patterns are given in Fig.1.1. The cosmological importance of the E-B decomposition stems from the result that linear, scalar (density) perturbations do not produce magnetic polarization (Seljak & Zaldarriaga 1997; Kamionkowski et al. 1997) since they give rise to a spatial pattern of the polarization field at last scattering that is curl-free. However, a cosmological background of gravitational waves (tensor modes), such as that generated in most models of inflation, produces both E-and 3 B-mode polarization with similar power in each mode. The power is concentrated around l~100 since the amplitude of gravitational waves damps once inside the horizon. The polarization from gravitational waves adds incoherently with that from density perturbations, but the E-B decomposition allows the two contributions to be cleanly disentangled. Vortical motion of the primordial plasma, due to vector modes at last scattering, would also produce B-mode polarization, but vector modes are only expected to be significant in models with active generation of perturbations (e.g. defect models). Such models are definitively ruled out as the main source of structure formation by current CMB temperature anisotropy data. A detection of large-angle, primordial magnetic polarization in the CMB would thus be very strong evidence for a cosmological background of gravitational waves. An additional source of magnetic polarization arises from weak gravitational lensing of CMB photons by large-scale structure. These deflections re-map the curl-free pattern of polarization from density perturbations, redistributing some E-mode power into B-mode, even in the absence of gravitational waves (Zaldarriaga & Seljak 1998). The various theoretical power spectra of the polarization and temperature anisotropies are shown in Figure 1.2 for the concordance flat, L-CDM model (Spergel et al. 2003) with optical depth through reionization t=0.148. The density fluctuations are adiabatic with spectral index 2 ns=0.96 , and the tensor-to-scalar ratio r =0.15 appropriate to chaotic (f ) inflation. Only the temperature anisotropy spectrum has been mapped accurately to date, but the E and B TE power spectra, and the lensing contribution to C l , can be predicted with reasonable accuracy from current data. However, the amplitude of the gravitational wave background is subject only to weak upper bounds by the anisotropy data. Although the amplitude of is not known, its shape is robust since it depends mainly on cosmological parameters that are already well constrained. 1.2: Current status of cosmic microwave background polarimetry A detection of the polarization of the CMB was first announced in 2002 by the Degree Angular Scale Interferometer team (DASI; Kovac et al. 2002). They report a five-sigma detection of electric polarization, but no evidence for magnetic polarization in their data. These conclusions 4 have been reiforced but not changed significantly by the recently published analysis of 3 years of data from DASI (Leitch et al. 2004). The CBI experiment has also detected E-modes polarization at smaller scales, and with a similar significance (Readhead et al. 2004). At the time of writing the only other published detection is of the TE cross-correlation from the one- year WMAP data (Kogut et al. 2003). The DASI, CBI and WMAP detections have already had considerable scientific impact: •The presence of acoustic oscillations in the TE and E power spectra with precisely the phase relation and amplitude to the temperature spectrum that is predicted for passive, adiabatic fluctuations, lends further support to this paradigm for structure formation, and allows strong upper limits to be placed on the amplitude of isocurvature fluctuations (Peiris et al. 2003; Gordon & Lewis 2003). •The detection of a correlation between polarization and temperature around l~150 is clear evidence for adiabatic, apparently super-horizon fluctuations at last scattering. Inflation is the simplest, causal mechanism for generating such fluctuations. •The excess power on large scales in the cross-correlation of T and E, seen by WMAP, points to early (and complex) reionization with optical depth t˜0.17 (based on a fit to the TE power spectrum alone). As already noted, B-mode polarization of the CMB is currently subject only to weak upper limits. The best limit on large scales, l~10, is from the POLAR experiment (Keating et al. 2001), while the best limits on smaller scales are from DASI . These (95-per cent) upper limits are shown in Figure 1.4. Although the current upper limit on r from B-mode polarization is much weaker than that inferred from the CMB temperature anisotropies, the former route has the potential to detect much lower levels of r with improvements in instrumentation, but the latter route is limited by the inescapable cosmic variance of the dominant density- perturbation signal in the temperature anisotropies. Indeed, a perfect temperature-anisotropy experiment can only detect r>0.07, even assuming all other parameters are known. Supplementing the temperature anisotropies with electric polarization makes only a modest further improvement. 5 1.3 The scientific case for CLOVER 1.3.1: Mapping the B-mode power spectrum The main science goal of CLOVER is to measure the power spectrum of B -mode polarization in the multipole range 20–1000.
Load more

Recommended publications
  • The WMAP Results and Cosmology
    The WMAP results and cosmology Rachel Bean Cornell University SLAC Summer Institute July 19th 2006 Rachel Bean : SSI July 29th 2006 1/44 Plan o Overview o Introduction to CMB temperature and polarization o The maps and spectra o Cosmological implications Rachel Bean : SSI July 29th 2006 2/44 What is WMAP? o Satellite detecting primordial photons “cosmic microwave background” Rachel Bean : SSI July 29th 2006 3/44 Science Team C. Barnes (Princeton) N. Odegard (GSFC) R. Bean (Cornell) L. Page (Princeton) C. Bennett (JHU) D. Spergel (Princeton) O. Dore (CITA) G. Tucker (Brown) M. Halpern (UBC) L. Verde (Penn) R. Hill (GSFC) J. Weiland (GSFC) G. Hinshaw (GSFC) E. Wollack (GSFC) N. Jarosik (Princeton) A. Kogut (GSFC) E. Komatsu (Texas) M. Limon (GSFC) S. Meyer (Chicago) H. Peiris (Chicago) M. Nolta (CITA) Rachel Bean : SSI July 29th 2006 4/44 Plan o Overview o Introduction to CMB temperature and polarization o The maps and spectra o Cosmological implications Rachel Bean : SSI July 29th 2006 5/44 CMB is a near perfect primordial blackbody spectrum Universe expanding and cooling over time… Kinney 1) Optically opaque plasma photons scattering off electrons 3) ‘Free Streaming’ CMB Thermalized (blackbody) photons at 2) The ‘last scattering’ of photons ~6000K diluted and redshifted by ~300,000 years after the Big Bang, universe’s expansion -> ~2.726K neutral atoms form and photons stop background we measure today. interacting with them. Rachel Bean : SSI July 29th 2006 6/44 The oldest fossil from the early universe Recombination CMB Nucleosynthesis Processes during opaque era imprint in CMB fluctuations Inflation and Grand Unification? Quantum Gravity/ Trans-Planckian effects….
    [Show full text]
  • Proceedings of Spie
    PROCEEDINGS OF SPIE SPIEDigitalLibrary.org/conference-proceedings-of-spie Survey strategy optimization for the Atacama Cosmology Telescope De Bernardis, F., Stevens, J., Hasselfield, M., Alonso, D., Bond, J. R., et al. F. De Bernardis, J. R. Stevens, M. Hasselfield, D. Alonso, J. R. Bond, E. Calabrese, S. K. Choi, K. T. Crowley, M. Devlin, J. Dunkley, P. A. Gallardo, S. W. Henderson, M. Hilton, R. Hlozek, S. P. Ho, K. Huffenberger, B. J. Koopman, A. Kosowsky, T. Louis, M. S. Madhavacheril, J. McMahon, S. Næss, F. Nati, L. Newburgh, M. D. Niemack, L. A. Page, M. Salatino, A. Schillaci, B. L. Schmitt, N. Sehgal, J. L. Sievers, S. M. Simon, D. N. Spergel, S. T. Staggs, A. van Engelen, E. M. Vavagiakis, E. J. Wollack, "Survey strategy optimization for the Atacama Cosmology Telescope," Proc. SPIE 9910, Observatory Operations: Strategies, Processes, and Systems VI, 991014 (15 July 2016); doi: 10.1117/12.2232824 Event: SPIE Astronomical Telescopes + Instrumentation, 2016, Edinburgh, United Kingdom Downloaded From: https://www.spiedigitallibrary.org/conference-proceedings-of-spie on 06 Oct 2020 Terms of Use: https://www.spiedigitallibrary.org/terms-of-use Survey strategy optimization for the Atacama Cosmology Telescope F. De Bernardisa, J. R. Stevensa, M. Hasselfieldb,c, D. Alonsod, J. R. Bonde, E. Calabresed, S. K. Choif, K. T. Crowleyf, M. Devling, J. Dunkleyd, P. A. Gallardoa, S. W. Hendersona, M. Hiltonh, R. Hlozeki, S. P. Hof, K. Huffenbergerj, B. J. Koopmana, A. Kosowskyk, T. Louisl, M. S. Madhavacherilm, J. McMahonn, S. Naessd, F. Natig, L. Newburghi, M. D. Niemacka, L. A. Pagef, M. Salatinof, A.
    [Show full text]
  • Analysis and Measurement of Horn Antennas for CMB Experiments
    Analysis and Measurement of Horn Antennas for CMB Experiments Ian Mc Auley (M.Sc. B.Sc.) A thesis submitted for the Degree of Doctor of Philosophy Maynooth University Department of Experimental Physics, Maynooth University, National University of Ireland Maynooth, Maynooth, Co. Kildare, Ireland. October 2015 Head of Department Professor J.A. Murphy Research Supervisor Professor J.A. Murphy Abstract In this thesis the author's work on the computational modelling and the experimental measurement of millimetre and sub-millimetre wave horn antennas for Cosmic Microwave Background (CMB) experiments is presented. This computational work particularly concerns the analysis of the multimode channels of the High Frequency Instrument (HFI) of the European Space Agency (ESA) Planck satellite using mode matching techniques to model their farfield beam patterns. To undertake this analysis the existing in-house software was upgraded to address issues associated with the stability of the simulations and to introduce additional functionality through the application of Single Value Decomposition in order to recover the true hybrid eigenfields for complex corrugated waveguide and horn structures. The farfield beam patterns of the two highest frequency channels of HFI (857 GHz and 545 GHz) were computed at a large number of spot frequencies across their operational bands in order to extract the broadband beams. The attributes of the multimode nature of these channels are discussed including the number of propagating modes as a function of frequency. A detailed analysis of the possible effects of manufacturing tolerances of the long corrugated triple horn structures on the farfield beam patterns of the 857 GHz horn antennas is described in the context of the higher than expected sidelobe levels detected in some of the 857 GHz channels during flight.
    [Show full text]
  • CMB Beam Systematics: Impact on Lensing Parameter Estimation
    CMB Beam Systematics: Impact on Lensing Parameter Estimation N.J. Miller, M. Shimon, B.G. Keating Center for Astrophysics and Space Sciences, University of California, San Diego, 9500 Gilman Drive, La Jolla, CA, 92093-0424 (Dated: January 26) The cosmic microwave background (CMB) is a rich source of cosmological information. Thanks to the simplicity and linearity of the theory of cosmological perturbations, observations of the CMB’s polarization and temperature anisotropy can reveal the parameters which describe the contents, structure, and evolution of the cosmos. Temperature anisotropy is necessary but not sufficient to fully mine the CMB of its cosmological information as it is plagued with various parameter degenera- cies. Fortunately, CMB polarization breaks many of these degeneracies and adds new information and increased precision. Of particular interest is the CMB’s B-mode polarization which provides a handle on several cosmological parameters most notably the tensor-to-scalar ratio, r, and is sen- sitive to parameters which govern the growth of large scale structure (LSS) and evolution of the gravitational potential. These imprint CMB temperature anisotropy and cause E-to-B-mode po- larization conversion via gravitational lensing. However, both primordial gravitational-wave- and secondary lensing-induced B-mode signals are very weak and therefore prone to various foregrounds and systematics. In this work we use Fisher-matrix-based estimations and apply, for the first time, Monte-Carlo Markov Chain (MCMC) simulations to determine
    [Show full text]
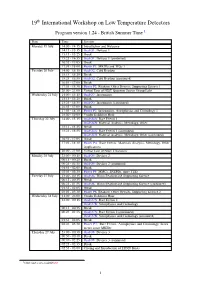
  • 19 International Workshop on Low Temperature Detectors
    19th International Workshop on Low Temperature Detectors Program version 1.24 - British Summer Time 1 Date Time Session Monday 19 July 14:00 - 14:15 Introduction and Welcome 14:15 - 15:15 Oral O1: Devices 1 15:15 - 15:25 Break 15:25 - 16:55 Oral O1: Devices 1 (continued) 16:55 - 17:05 Break 17:05 - 18:00 Poster P1: MKIDs and TESs 1 Tuesday 20 July 14:00 - 15:15 Oral O2: Cold Readout 15:15 - 15:25 Break 15:25 - 16:55 Oral O2: Cold Readout (continued) 16:55 - 17:05 Break 17:05 - 18:30 Poster P2: Readout, Other Devices, Supporting Science 1 20:00 - 21:00 Virtual Tour of NIST Quantum Sensor Group Labs Wednesday 21 July 14:00 - 15:15 Oral O3: Instruments 15:15 - 15:25 Break 15:25 - 16:55 Oral O3: Instruments (continued) 16:55 - 17:05 Break 17:05 - 18:30 Poster P3: Instruments, Astrophysics and Cosmology 1 18:00 - 19:00 Vendor Exhibitor Hour Thursday 22 July 14:00 - 15:15 Oral O4A: Rare Events 1 Oral O4B: Material Analysis, Metrology, Other 15:15 - 15:25 Break 15:25 - 16:55 Oral O4A: Rare Events 1 (continued) Oral O4B: Material Analysis, Metrology, Other (continued) 16:55 - 17:05 Break 17:05 - 18:30 Poster P4: Rare Events, Materials Analysis, Metrology, Other Applications 20:00 - 21:00 Virtual Tour of NIST Cleanoom Monday 26 July 23:00 - 00:15 Oral O5: Devices 2 00:15 - 00:25 Break 00:25 - 01:55 Oral O5: Devices 2 (continued) 01:55 - 02:05 Break 02:05 - 03:30 Poster P5: MMCs, SNSPDs, more TESs Tuesday 27 July 23:00 - 00:15 Oral O6: Warm Readout and Supporting Science 00:15 - 00:25 Break 00:25 - 01:55 Oral O6: Warm Readout and Supporting Science
    [Show full text]
  • Maturity of Lumped Element Kinetic Inductance Detectors For
    Astronomy & Astrophysics manuscript no. Catalano˙f c ESO 2018 September 26, 2018 Maturity of lumped element kinetic inductance detectors for space-borne instruments in the range between 80 and 180 GHz A. Catalano1,2, A. Benoit2, O. Bourrion1, M. Calvo2, G. Coiffard3, A. D’Addabbo4,2, J. Goupy2, H. Le Sueur5, J. Mac´ıas-P´erez1, and A. Monfardini2,1 1 LPSC, Universit Grenoble-Alpes, CNRS/IN2P3, 2 Institut N´eel, CNRS, Universit´eJoseph Fourier Grenoble I, 25 rue des Martyrs, Grenoble, 3 Institut de Radio Astronomie Millim´etrique (IRAM), Grenoble, 4 LNGS - Laboratori Nazionali del Gran Sasso - Assergi (AQ), 5 Centre de Sciences Nucl´eaires et de Sciences de la Mati`ere (CSNSM), CNRS/IN2P3, bat 104 - 108, 91405 Orsay Campus Preprint online version: September 26, 2018 ABSTRACT This work intends to give the state-of-the-art of our knowledge of the performance of lumped element kinetic inductance detectors (LEKIDs) at millimetre wavelengths (from 80 to 180 GHz). We evaluate their optical sensitivity under typical background conditions that are representative of a space environment and their interaction with ionising particles. Two LEKID arrays, originally designed for ground-based applications and composed of a few hundred pixels each, operate at a central frequency of 100 and 150 GHz (∆ν/ν about 0.3). Their sensitivities were characterised in the laboratory using a dedicated closed-cycle 100 mK dilution cryostat and a sky simulator, allowing for the reproduction of realistic, space-like observation conditions. The impact of cosmic rays was evaluated by exposing the LEKID arrays to alpha particles (241Am) and X sources (109Cd), with a read-out sampling frequency similar to those used for Planck HFI (about 200 Hz), and also with a high resolution sampling level (up to 2 MHz) to better characterise and interpret the observed glitches.
    [Show full text]
  • CMB Telescopes and Optical Systems to Appear In: Planets, Stars and Stellar Systems (PSSS) Volume 1: Telescopes and Instrumentation
    CMB Telescopes and Optical Systems To appear in: Planets, Stars and Stellar Systems (PSSS) Volume 1: Telescopes and Instrumentation Shaul Hanany ([email protected]) University of Minnesota, School of Physics and Astronomy, Minneapolis, MN, USA, Michael Niemack ([email protected]) National Institute of Standards and Technology and University of Colorado, Boulder, CO, USA, and Lyman Page ([email protected]) Princeton University, Department of Physics, Princeton NJ, USA. March 26, 2012 Abstract The cosmic microwave background radiation (CMB) is now firmly established as a funda- mental and essential probe of the geometry, constituents, and birth of the Universe. The CMB is a potent observable because it can be measured with precision and accuracy. Just as importantly, theoretical models of the Universe can predict the characteristics of the CMB to high accuracy, and those predictions can be directly compared to observations. There are multiple aspects associated with making a precise measurement. In this review, we focus on optical components for the instrumentation used to measure the CMB polarization and temperature anisotropy. We begin with an overview of general considerations for CMB ob- servations and discuss common concepts used in the community. We next consider a variety of alternatives available for a designer of a CMB telescope. Our discussion is guided by arXiv:1206.2402v1 [astro-ph.IM] 11 Jun 2012 the ground and balloon-based instruments that have been implemented over the years. In the same vein, we compare the arc-minute resolution Atacama Cosmology Telescope (ACT) and the South Pole Telescope (SPT). CMB interferometers are presented briefly. We con- clude with a comparison of the four CMB satellites, Relikt, COBE, WMAP, and Planck, to demonstrate a remarkable evolution in design, sensitivity, resolution, and complexity over the past thirty years.
    [Show full text]
  • The Design of the Ali CMB Polarization Telescope Receiver
    The design of the Ali CMB Polarization Telescope receiver M. Salatinoa,b, J.E. Austermannc, K.L. Thompsona,b, P.A.R. Aded, X. Baia,b, J.A. Beallc, D.T. Beckerc, Y. Caie, Z. Changf, D. Cheng, P. Chenh, J. Connorsc,i, J. Delabrouillej,k,e, B. Doberc, S.M. Duffc, G. Gaof, S. Ghoshe, R.C. Givhana,b, G.C. Hiltonc, B. Hul, J. Hubmayrc, E.D. Karpela,b, C.-L. Kuoa,b, H. Lif, M. Lie, S.-Y. Lif, X. Lif, Y. Lif, M. Linkc, H. Liuf,m, L. Liug, Y. Liuf, F. Luf, X. Luf, T. Lukasc, J.A.B. Matesc, J. Mathewsonn, P. Mauskopfn, J. Meinken, J.A. Montana-Lopeza,b, J. Mooren, J. Shif, A.K. Sinclairn, R. Stephensonn, W. Sunh, Y.-H. Tsengh, C. Tuckerd, J.N. Ullomc, L.R. Valec, J. van Lanenc, M.R. Vissersc, S. Walkerc,i, B. Wange, G. Wangf, J. Wango, E. Weeksn, D. Wuf, Y.-H. Wua,b, J. Xial, H. Xuf, J. Yaoo, Y. Yaog, K.W. Yoona,b, B. Yueg, H. Zhaif, A. Zhangf, Laiyu Zhangf, Le Zhango,p, P. Zhango, T. Zhangf, Xinmin Zhangf, Yifei Zhangf, Yongjie Zhangf, G.-B. Zhaog, and W. Zhaoe aStanford University, Stanford, CA 94305, USA bKavli Institute for Particle Astrophysics and Cosmology, Stanford, CA 94305, USA cNational Institute of Standards and Technology, Boulder, CO 80305, USA dCardiff University, Cardiff CF24 3AA, United Kingdom eUniversity of Science and Technology of China, Hefei 230026 fInstitute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049 gNational Astronomical Observatories, Chinese Academy of Sciences, Beijing 100012 hNational Taiwan University, Taipei 10617 iUniversity of Colorado Boulder, Boulder, CO 80309, USA jIN2P3, CNRS, Laboratoire APC, Universit´ede Paris, 75013 Paris, France kIRFU, CEA, Universit´eParis-Saclay, 91191 Gif-sur-Yvette, France lBeijing Normal University, Beijing 100875 mAnhui University, Hefei 230039 nArizona State University, Tempe, AZ 85004, USA oShanghai Jiao Tong University, Shanghai 200240 pSun Yat-Sen University, Zhuhai 519082 ABSTRACT Ali CMB Polarization Telescope (AliCPT-1) is the first CMB degree-scale polarimeter to be deployed on the Tibetan plateau at 5,250 m above sea level.
    [Show full text]
  • Arxiv:1412.0626V1 [Astro-Ph.CO] 1 Dec 2014 Versity, 3400 N
    Draft: December 2, 2014 Preprint typeset using LATEX style emulateapj v. 05/12/14 THE ATACAMA COSMOLOGY TELESCOPE: LENSING OF CMB TEMPERATURE AND POLARIZATION DERIVED FROM COSMIC INFRARED BACKGROUND CROSS-CORRELATION Alexander van Engelen1,2, Blake D. Sherwin3, Neelima Sehgal2, Graeme E. Addison4, Rupert Allison5, Nick Battaglia6, Francesco de Bernardis7, J. Richard Bond1, Erminia Calabrese5, Kevin Coughlin8, Devin Crichton9, Rahul Datta8, Mark J. Devlin10, Joanna Dunkley5, Rolando Dunner¨ 11, Emily Grace12, Megan Gralla9, Amir Hajian1, Matthew Hasselfield13,4, Shawn Henderson7, J. Colin Hill14, Matt Hilton15, Adam D. Hincks4, Renee´ Hlozek13, Kevin M. Huffenberger16, John P. Hughes17, Brian Koopman7, Arthur Kosowsky18, Thibaut Louis5, Marius Lungu10, Mathew Madhavacheril2, Lo¨ıc Maurin11, Jeff McMahon8, Kavilan Moodley15, Charles Munson8, Sigurd Naess5, Federico Nati19, Laura Newburgh20, Michael D. Niemack7, Michael R. Nolta1, Lyman A. Page12, Christine Pappas12, Bruce Partridge21, Benjamin L. Schmitt10, Jonathan L. Sievers22,23,12, Sara Simon12, David N. Spergel13, Suzanne T. Staggs12, Eric R. Switzer24,1, Jonathan T. Ward10, Edward J. Wollack24 Draft: December 2, 2014 ABSTRACT We present a measurement of the gravitational lensing of the Cosmic Microwave Background (CMB) temperature and polarization fields obtained by cross-correlating the reconstructed convergence signal from the first season of ACTPol data at 146 GHz with Cosmic Infrared Background (CIB) fluctu- ations measured using the Planck satellite. Using an overlap area of 206 square degrees, we detect gravitational lensing of the CMB polarization by large-scale structure at a statistical significance of 4:5σ. Combining both CMB temperature and polarization data gives a lensing detection at 9:1σ sig- nificance. A B-mode polarization lensing signal is present with a significance of 3:2σ.
    [Show full text]
  • Searching for the Missing Baryons in Clusters
    Searching for the missing baryons in clusters Bilhuda Rasheed, Neta Bahcall1, and Paul Bode Department of Astrophysical Sciences, 4 Ivy Lane, Peyton Hall, Princeton University, Princeton, NJ 08544 Edited by Marc Davis, University of California, Berkeley, CA, and approved January 10, 2011 (received for review July 8, 2010) Observations of clusters of galaxies suggest that they contain few- fraction in the richest clusters, it is still systematically below er baryons (gas plus stars) than the cosmic baryon fraction. This the cosmic value. This baryon discrepancy, especially the gas frac- “missing baryon” puzzle is especially surprising for the most mas- tion, is observed to increase with decreasing cluster mass (14, 15). sive clusters, which are expected to be representative of the cosmic This raises the questions: Where are the missing baryons? Why matter content of the universe (baryons and dark matter). Here we are they “missing”? show that the baryons may not actually be missing from clusters, Attempted explanations for the missing baryons in clusters but rather are extended to larger radii than typically observed. The range from preheating or other energy inputs that expel gas from baryon deficiency is typically observed in the central regions of the system (16–22, and references therein), to the suggestion of clusters (∼0.5 the virial radius). However, the observed gas-density additional baryonic components not yet detected [e.g., cool gas, profile is significantly shallower than the mass-density profile, faint stars (10, 23)]. Simulations, which do suggest a depletion of implying that the gas is more extended than the mass and that cluster gas in the inner regions of clusters, do not yet contain all the gas fraction increases with radius.
    [Show full text]
  • Calibration of a Polarimetric Microwave Radiometer Using a Double Directional Coupler
    remote sensing Article Calibration of a Polarimetric Microwave Radiometer Using a Double Directional Coupler Luisa de la Fuente 1,* , Beatriz Aja 1 , Enrique Villa 2 and Eduardo Artal 1 1 Departamento de Ingeniería de Comunicaciones, Universidad de Cantabria, 39005 Santander, Spain; [email protected] (B.A.); [email protected] (E.A.) 2 IACTEC, Instituto de Astrofísica de Canarias, 38205 La Laguna, Spain; [email protected] * Correspondence: [email protected] Abstract: This paper presents a built-in calibration procedure of a 10-to-20 GHz polarimeter aimed at measuring the I, Q, U Stokes parameters of cosmic microwave background (CMB) radiation. A full-band square waveguide double directional coupler, mounted in the antenna-feed system, is used to inject differently polarized reference waves. A brief description of the polarimetric microwave radiometer and the system calibration injector is also reported. A fully polarimetric calibration is also possible using the designed double directional coupler, although the presented calibration method in this paper is proposed to obtain three of the four Stokes parameters with the introduced microwave receiver, since V parameter is expected to be zero for the CMB radiation. Experimental results are presented for linearly polarized input waves in order to validate the built-in calibration system. Keywords: radiometer; polarimeter calibration; microwave polarimeter; radiometer calibration; radio astronomy receiver; cosmic microwave background receiver; Stokes parameters Citation: de la Fuente, L.; Aja, B.; Villa, E.; Artal, E. Calibration of a 1. Introduction Polarimetric Microwave Radiometer Remote sensing applications employ sensitive instruments to fulfill the scientific goals Using a Double Directional Coupler. of dedicated missions or projects, either space or terrestrial.
    [Show full text]
  • The Atacama Cosmology Telescope (Act): Beam Profiles and First Sz Cluster Maps
    ApJS, 191 :423-438, 20 I 0 DECEMBER Preprint typeset using ""TEX style emulateapj v. 11/10/09 THE ATACAMA COSMOLOGY TELESCOPE (ACT): BEAM PROFILES AND FIRST SZ CLUSTER MAPS A, D, HINCKS I, V, ACQUAVIVA 2,3, p, A, R, ADE4, p, AGUIRRES, M, AMIRI6, J, W, ApPEL I, L. F, BARRIENTOS5, E, S, BATTISTELU7,6, 9 6 IO I I2 12 13 J, R, BONDs, B, BROWN , B, BURGER , 1. CHERVENAK , S, DAS I.I.3, M, J. DEVLIN , S. R. DICKER , W, B, DORIESE , I4 1 3 5 I I s 6 J. DUNKLEy . , R. DONNER , T. ESSINGER-HILEMAN , R. P. FISHER , J. W. FOWLER I , A. HAJIAN ,3.1, M. HALPERN , 6 I5 13 I6 17 I4 I8 M. HASSELFIELD , C, HERNANDEZ-MONTEAGUDO , G, C. HILTON , M. HILTON . , R. HLOZEK , K, M. HUFFENBERGER , I9 2 5 I3 20 5 I2 I2 D. H. HUGHES , J. P. HUGHES , L. INFANTE , K. D. IRWIN , R, JIMENEZ , J. B. JUIN , M. KAUL , J. KLEIN , A. KOSOWSKy9, 23 12 24 3 25 3 I2 26 4 J. M, LAU21.22.1 , M, LIMON . ,! , Y-T. LIN . .5, R, H. LUPTON), T. A. MARRIAGE . , D. MARSDEN , K, MARTOCCI ), p, MAUSKOPF , 2 27 8 F. MENANTEAU , K. MOODLEyI6.I7, H. MOSELEYIO, C. B. NETTERFIELD , M. D. NIEMACK 13.1, M. R. NOLTA , L, A. PAGE I, I 28 5 20 1 21 8 I L. PARKER , B. PARTRIDGE , H, QUINTANA , B. REID . , N. SEHGAL , J. SIEVERS , D. N. SPERGEL 3, S. T. STAGGS , 0. STRYZAK I, I2 13 26 I2 29 30 20 I6 31 D.
    [Show full text]