Mindstorms: Children, Computers, and Powerful Ideas
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

REFERENCE DOCUMENT Containing the Annual Financial Report Fiscal Year 2016 PROFILE
REFERENCE DOCUMENT containing the Annual Financial Report Fiscal Year 2016 PROFILE The Lagardère group is a global leader in content publishing, production, broadcasting and distribution, whose powerful brands leverage its virtual and physical networks to attract and enjoy qualifi ed audiences. The Group’s business model relies on creating a lasting and exclusive relationship between the content it offers and its customers. It is structured around four business divisions: • Books and e-Books: Lagardère Publishing • Travel Essentials, Duty Free & Fashion, and Foodservice: Lagardère Travel Retail • Press, Audiovisual (Radio, Television, Audiovisual Production), Digital and Advertising Sales Brokerage: Lagardère Active • Sponsorship, Content, Consulting, Events, Athletes, Stadiums, Shows, Venues and Artists: Lagardère Sports and Entertainment 1945: at the end of World 1986: Hachette regains 26 March 2003: War II, Marcel Chassagny founds control of Europe 1. Arnaud Lagardère is appointed Matra (Mécanique Aviation Managing Partner of TRAction), a company focused 10 February 1988: Lagardère SCA. on the defence industry. Matra is privatised. 2004: the Group acquires 1963: Jean-Luc Lagardère 30 December 1992: a portion of Vivendi Universal becomes Chief Executive Publishing’s French and following the failure of French Offi cer of Matra, which Spanish assets. television channel La Cinq, has diversifi ed into aerospace Hachette is merged into Matra and automobiles. to form Matra-Hachette, 2007: the Group reorganises and Lagardère Groupe, a French around four major institutional 1974: Sylvain Floirat asks partnership limited by shares, brands: Lagardère Publishing, Jean-Luc Lagardère to head is created as the umbrella Lagardère Services (which the Europe 1 radio network. company for the entire became Lagardère Travel Retail ensemble. -

A Universal Modular ACTOR Formalism for Artificial
Artificial Intelligence A Universal Modular ACTOR Formalism for Artificial Intelligence Carl Hewitt Peter Bishop Richard Steiger Abstract This paper proposes a modular ACTOR architecture and definitional method for artificial intelligence that is conceptually based on a single kind of object: actors [or, if you will, virtual processors, activation frames, or streams]. The formalism makes no presuppositions about the representation of primitive data structures and control structures. Such structures can be programmed, micro-coded, or hard wired 1n a uniform modular fashion. In fact it is impossible to determine whether a given object is "really" represented as a list, a vector, a hash table, a function, or a process. The architecture will efficiently run the coming generation of PLANNER-like artificial intelligence languages including those requiring a high degree of parallelism. The efficiency is gained without loss of programming generality because it only makes certain actors more efficient; it does not change their behavioral characteristics. The architecture is general with respect to control structure and does not have or need goto, interrupt, or semaphore primitives. The formalism achieves the goals that the disallowed constructs are intended to achieve by other more structured methods. PLANNER Progress "Programs should not only work, but they should appear to work as well." PDP-1X Dogma The PLANNER project is continuing research in natural and effective means for embedding knowledge in procedures. In the course of this work we have succeeded in unifying the formalism around one fundamental concept: the ACTOR. Intuitively, an ACTOR is an active agent which plays a role on cue according to a script" we" use the ACTOR metaphor to emphasize the inseparability of control and data flow in our model. -

Issue Hero Villain Place Result Avengers Spotlight #26 Iron Man
Issue Hero Villain Place Result Avengers Spotlight #26 Iron Man, Hawkeye Wizard, other villains Vault Breakout stopped, but some escape New Mutants #86 Rusty, Skids Vulture, Tinkerer, Nitro Albany Everyone Arrested Damage Control #1 John, Gene, Bart, (Cap) Wrecking Crew Vault Thunderball and Wrecker escape Avengers #311 Quasar, Peggy Carter, other Avengers employees Doombots Avengers Hydrobase Hydrobase destroyed Captain America #365 Captain America Namor (controlled by Controller) Statue of Liberty Namor defeated Fantastic Four #334 Fantastic Four Constrictor, Beetle, Shocker Baxter Building FF victorious Amazing Spider-Man #326 Spiderman Graviton Daily Bugle Graviton wins Spectacular Spiderman #159 Spiderman Trapster New York Trapster defeated, Spidey gets cosmic powers Wolverine #19 & 20 Wolverine, La Bandera Tiger Shark Tierra Verde Tiger Shark eaten by sharks Cloak & Dagger #9 Cloak, Dagger, Avengers Jester, Fenris, Rock, Hydro-man New York Villains defeated Web of Spiderman #59 Spiderman, Puma Titania Daily Bugle Titania defeated Power Pack #53 Power Pack Typhoid Mary NY apartment Typhoid kills PP's dad, but they save him. Incredible Hulk #363 Hulk Grey Gargoyle Las Vegas Grey Gargoyle defeated, but escapes Moon Knight #8-9 Moon Knight, Midnight, Punisher Flag Smasher, Ultimatum Brooklyn Ultimatum defeated, Flag Smasher killed Doctor Strange #11 Doctor Strange Hobgoblin, NY TV studio Hobgoblin defeated Doctor Strange #12 Doctor Strange, Clea Enchantress, Skurge Empire State Building Enchantress defeated Fantastic Four #335-336 Fantastic -

Compiler Error Messages Considered Unhelpful: the Landscape of Text-Based Programming Error Message Research
Working Group Report ITiCSE-WGR ’19, July 15–17, 2019, Aberdeen, Scotland Uk Compiler Error Messages Considered Unhelpful: The Landscape of Text-Based Programming Error Message Research Brett A. Becker∗ Paul Denny∗ Raymond Pettit∗ University College Dublin University of Auckland University of Virginia Dublin, Ireland Auckland, New Zealand Charlottesville, Virginia, USA [email protected] [email protected] [email protected] Durell Bouchard Dennis J. Bouvier Brian Harrington Roanoke College Southern Illinois University Edwardsville University of Toronto Scarborough Roanoke, Virgina, USA Edwardsville, Illinois, USA Scarborough, Ontario, Canada [email protected] [email protected] [email protected] Amir Kamil Amey Karkare Chris McDonald University of Michigan Indian Institute of Technology Kanpur University of Western Australia Ann Arbor, Michigan, USA Kanpur, India Perth, Australia [email protected] [email protected] [email protected] Peter-Michael Osera Janice L. Pearce James Prather Grinnell College Berea College Abilene Christian University Grinnell, Iowa, USA Berea, Kentucky, USA Abilene, Texas, USA [email protected] [email protected] [email protected] ABSTRACT of evidence supporting each one (historical, anecdotal, and empiri- Diagnostic messages generated by compilers and interpreters such cal). This work can serve as a starting point for those who wish to as syntax error messages have been researched for over half of a conduct research on compiler error messages, runtime errors, and century. Unfortunately, these messages which include error, warn- warnings. We also make the bibtex file of our 300+ reference corpus ing, and run-time messages, present substantial difficulty and could publicly available. -

Agent-Based Modeling with Netlogo
Agent-Based Modeling with NetLogo Uri Wilensky Center for Connected Learning and Computer-Based Modeling Northwestern Institute on Complex Systems Departments of Computer Science & Learning Sciences Northwestern University Agent-Based Modeling in NetLogo SFI MOOC, Summer 2016 1 History: Roman to Hindu-Arabic Europe – at the turn of the first millenium • Before widespread adoption of Hindu-Arabic, very few could do multiplication/division • Scientists recognized superiority immediately • But widespread adoption took a very long time • Was in surreptitious use, but not official 2 Restructurations Structurations -- the encoding of the knowledge in a domain as a function of the representational infrastructure used to express the knowledge Restructurations -- A change from one structuration of a domain to another resulting from a change in representational infrastructure --- Wilensky & Papert 2006;2010 What is important and hard for people today? Similar to numeracy importance for science but difficulties in understanding, today we need to make sense of complex systems yet we find it difficult. What are Complex Systems? • Systems with a large number of interacting parts, evolving over time • Decentralized decisions vs. centralized control • Emergent global patterns from local interactions and decisions • Examples: ecosystems, economies, immune systems, molecular systems, minds, stock market, democratic government... Emergent Phenomena • Structure (Rules) at Micro- level leads to pattern at Macro- level • Order without Design • No leader or orchestrator -

Inspiring Mathematical Creativity Through Juggling
Journal of Humanistic Mathematics Volume 10 | Issue 2 July 2020 Inspiring Mathematical Creativity through Juggling Ceire Monahan Montclair State University Mika Munakata Montclair State University Ashwin Vaidya Montclair State University Sean Gandini Follow this and additional works at: https://scholarship.claremont.edu/jhm Part of the Arts and Humanities Commons, and the Mathematics Commons Recommended Citation Monahan, C. Munakata, M. Vaidya, A. and Gandini, S. "Inspiring Mathematical Creativity through Juggling," Journal of Humanistic Mathematics, Volume 10 Issue 2 (July 2020), pages 291-314. DOI: 10.5642/ jhummath.202002.14 . Available at: https://scholarship.claremont.edu/jhm/vol10/iss2/14 ©2020 by the authors. This work is licensed under a Creative Commons License. JHM is an open access bi-annual journal sponsored by the Claremont Center for the Mathematical Sciences and published by the Claremont Colleges Library | ISSN 2159-8118 | http://scholarship.claremont.edu/jhm/ The editorial staff of JHM works hard to make sure the scholarship disseminated in JHM is accurate and upholds professional ethical guidelines. However the views and opinions expressed in each published manuscript belong exclusively to the individual contributor(s). The publisher and the editors do not endorse or accept responsibility for them. See https://scholarship.claremont.edu/jhm/policies.html for more information. Inspiring Mathematical Creativity Through Juggling Ceire Monahan Department of Mathematical Sciences, Montclair State University, New Jersey, USA -
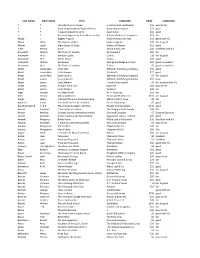
LAST NAME FIRST NAME TITLE PUBLISHER PRICE CONDITION ? ? the Life of Fancis Covell E
LAST NAME FIRST NAME TITLE PUBLISHER PRICE CONDITION ? ? The Life of Fancis Covell E. Wilmshurst, Blackheath $15 poor to fair ? ? Good Housekeeping's Book of Meals Good Housekeepind $23 poor ? ? A Supreme Book for Girls Dean & Son $10 good ? ? Personal Hygiene for Every Man and Boy A Social Guidance Enterprises $13 fair Abbey J. Biggles in Spain Oxford University Press $13 good with d/c Abbot Willis The Nations at War Leslie-Judge Co. $35 fair to good Abbott Jacob Mary Queen of Scots Makers of History $12 good Adler Renata Gone Simon & Schuster $20 Excellent with d/c Ainsworth William The Tower of London W. Foulsham $20 fair Ainsworth W. H. Windsor Castle Collins $8 fair to good Ainsworth W. H. Old St. Paul's Collins $10 good Ainsworth William Rookwood George Routledge and Sons $13 good to excellent Ainsworth W. H. The Tower of London Collins $5 good to excellent Alcott Louisa May Little Men Whitman Publishing Company $10 good Alcott Louisa May Little Women Goldsmith $22 good Alcott Louisa May Eight Cousins Whitman Publishing Company $7 fair to good Alcott Louisa Rose in Bloom Whitman Publishing Company $15 poor Alcott Lousia Little Women Juvenile Productions $5 fair to good with d/c Alcott Louisa An Old-Fashion Girl Donohue $10 poor to fair Alcott Louisa Little Women Saalfield $18 fair Alger Horatio In a New World M. A. Donohue $12 fair Allen Hervey Anthony Adverse Farrar and Rinehart Inc. $115 fair to good Angel Henry Practical Plane and Solid Geomerty William Collins, Sons $5 fair Appleton Victor Tom Swift and His Giant Robot Grosset & Dunlap $5 good Aquith & Bigland C. -

The Comparability Between Modular and Non-Modular
THE COMPARABILITY BETWEEN MODULAR AND NON-MODULAR EXAMINATIONS AT GCE ADVANCED LEVEL Elizabeth A Gray PhD INSTITUTE OF EDUCATION UNIVERSITY OF LONDON 1 ABSTRACT The prime concern of this thesis is the comparability of two types of assessment now prevalent in Advanced level GeE examinations. The more conventional linear scheme assesses all candidates terminally, and the only way to improve the grade awarded is to re-take the whole examination. In contrast, the relatively new modular schemes of assessment include testing opportunities throughout the course of study. This not only has formative effects but allows quantifiable improvements in syllabus results through the medium of the resit option. There are obvious differences between the two schemes, but this does not necessarily imply that they are not comparable in their grading standards. It is this standard which the thesis attempts to address by considering the different variabilities of each of the schemes, and how these might impinge upon the outcomes of the grading process as evidenced in the final grade distributions. A key issue is that of legitimate and illegitimate variabilities - the former perhaps allowing an improvement in performance while maintaining grading standards; the latter possibly affecting the grading standard because its effect was not fully taken into account in the awarding process. By looking at a linear and modular syllabus in mathematics, the differences between the two are investigated, and although not fully generalisable, it is clear that many of the worries which were advanced when modular schemes were first introduced are groundless. Most candidates are seen to use the testing flexibility to their advantage, but there is little evidence of over-testing. -

Microworlds: Building Powerful Ideas in the Secondary School
US-China Education Review A 9 (2012) 796-803 Earlier title: US-China Education Review, ISSN 1548-6613 D DAVID PUBLISHING Microworlds: Building Powerful Ideas in the Secondary School Craig William Jenkins University of Wales, Wales, UK In the 1960s, the MIT (Massachusetts Institute of Technology) developed a programming language called LOGO. Underpinning this invention was a profound new philosophy of how learners learn. This paper reviews research in the area and asks how one notion in particular, that of a microworld, may be used by secondary school educators to build powerful ideas in STEM (science, technology, engineering, and mathematics) subjects. Keywords: microworlds, programming, STEM (science, technology, engineering, and mathematics), constructionism, education Theories of Knowing This paper examines the microworld as a tool for acquiring powerful ideas in secondary education and explores their potential role in making relevant conceptual learning accessible through practical, constructionist approaches. In line with this aim, the paper is split into three main sections: The first section looks at the underlying educational theory behind microworlds in order to set up the rest of the paper; The second section critically examines the notion of a microworld in order to draw out the characteristics of a microworlds approach to learning; Finally, the paper ends with a real-world example of a microworld that is designed to build key, powerful ideas within a STEM (science, technology, engineering, and mathematics) domain of knowledge. To begin to understand the educational theory behind microworlds, a good starting point is to consider the ways in which learners interact with educational technology. In 1980, Robert Taylor (1980) provided a useful framework for understanding such interactions. -

An Algebraic Theory of Actors and Its Application to a Simple Object-Based Language
An Algebraic Theory of Actors and Its Application to a Simple Object-Based Language Gul Agha and Prasanna Thati University of Illinois at Urbana-Champaign, USA {agha,thati}@cs.uiuc.edu http://osl.cs.uiuc.edu/ 1 Introduction The development of Simula by Ole-Johan Dahl and Kristen Nygaard introduced a number of important programming language concepts – object which supports modularity in programming through encapsulation of data and procedures, the concept of class which organizes behavior and supports Abstract Data Types, and the concept inheritance which provides subtyping relations and reuse [6]. Peter Wegner terms programming languages which use objects as object-based languages, and reserves the term object-oriented languages for languages which also support classes and inheritance [58]. Concurrency provides a natural model for the execution of objects: in fact, Simula uses co-routines to simulate a simple form of concurrency in a sequen- tial execution environment. The resulting execution is tightly synchronized and, while this execution model is appropriate for simulations which use a global virtual clock, it is not an adequate model for distributed systems. The Actor Model unifies the notion of objects with concurrency; an actor is a concurrent object which operates asynchronously and interacts with other actors by sending asynchronous messages [2]. Many models for concurrent and distributed computation have been devel- oped. An early and influential model is Petri Nets developed by Carl Adam Petri [44]. In the Petri Net model, there are two kinds of elements – nodes and tokens. Nodes are connected to other nodes by fixed (static) links. Tokens are passed be- tween nodes using these links. -

In-Jest-Study-Guide
with Nels Ross “The Inspirational Oddball” . Study Guide ABOUT THE PRESENTER Nels Ross is an acclaimed performer and speaker who has won the hearts of international audiences. Applying his diverse background in performing arts and education, Nels works solo and with others to present school assemblies and programs which blend physical theater, variety arts, humor, and inspiration… All “in jest,” or in fun! ABOUT THE PROGRAM In Jest school assemblies and programs are based on the underlying principle that every person has value. Whether highlighting character, healthy choices, science & math, reading, or another theme, Nels employs physical theater and participation to engage the audience, juggling and other variety arts to teach the concepts, and humor to make it both fun and memorable. GOALS AND OBJECTIVES This program will enhance awareness and appreciation of physical theater and variety arts. In addition, the activities below provide connections to learning standards and the chosen theme. (What theme? Ask your artsineducation or assembly coordinator which specific program is coming to your school, and see InJest.com/schoolassemblyprograms for the latest description.) GETTING READY FOR THE PROGRAM ● Arrange for a clean, well lit SPACE, adjusting lights in advance as needed. Nels brings his own sound system, and requests ACCESS 4560 minutes before & after for set up & take down. ● Make announcements the day before to remind students and staff. For example: “Tomorrow we will have an exciting program with Nels Ross from In Jest. Be prepared to enjoy humor, juggling, and stunts in this uplifting celebration!” ● Discuss things which students might see and terms which they might not know: Physical Theater.. -

A Simplified Introduction to Virus Propagation Using Maple's Turtle Graphics Package
E. Roanes-Lozano, C. Solano-Macías & E. Roanes-Macías.: A simplified introduction to virus propagation using Maple's Turtle Graphics package A simplified introduction to virus propagation using Maple's Turtle Graphics package Eugenio Roanes-Lozano Instituto de Matemática Interdisciplinar & Departamento de Didáctica de las Ciencias Experimentales, Sociales y Matemáticas Facultad de Educación, Universidad Complutense de Madrid, Spain Carmen Solano-Macías Departamento de Información y Comunicación Facultad de CC. de la Documentación y Comunicación, Universidad de Extremadura, Spain Eugenio Roanes-Macías Departamento de Álgebra, Universidad Complutense de Madrid, Spain [email protected] ; [email protected] ; [email protected] Partially funded by the research project PGC2018-096509-B-100 (Government of Spain) 1 E. Roanes-Lozano, C. Solano-Macías & E. Roanes-Macías.: A simplified introduction to virus propagation using Maple's Turtle Graphics package 1. INTRODUCTION: TURTLE GEOMETRY AND LOGO • Logo language: developed at the end of the ‘60s • Characterized by the use of Turtle Geometry (a.k.a. as Turtle Graphics). • Oriented to introduce kids to programming (Papert, 1980). • Basic movements of the turtle (graphic cursor): FD, BK RT, LT. • It is not based on a Cartesian Coordinate system. 2 E. Roanes-Lozano, C. Solano-Macías & E. Roanes-Macías.: A simplified introduction to virus propagation using Maple's Turtle Graphics package • Initially robots were used to plot the trail of the turtle. http://cyberneticzoo.com/cyberneticanimals/1969-the-logo-turtle-seymour-papert-marvin-minsky-et-al-american/ 3 E. Roanes-Lozano, C. Solano-Macías & E. Roanes-Macías.: A simplified introduction to virus propagation using Maple's Turtle Graphics package • IBM Logo / LCSI Logo (’80) 4 E.