DOCSLIB.ORG

QUANTUM PHYSICS I a Muon Is a Particle Identical to an Electron Except Its Mass Is About 200 Times Larger. a Muonic Hydrogen Is

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
QUANTUM PHYSICS I a Muon Is a Particle Identical to an Electron Except Its Mass Is About 200 Times Larger. a Muonic Hydrogen Is QUANTUM PHYSICS I PROBLEM SET 5 - SOLUTION due November 10th before class A. Muonic hydrogen A muon is a particle identical to an electron except its mass is about 200 times larger. A muonic hydrogen is a bound state of a proton to a muon (instead of a proton and an electron as in the usual hydrogen). i) Use Bohr's theory to calculate the energy levels of the muonic hydrogen. What is the energy of the ground state (in eV ) ? We proceed as we (well, Bohr) did in the regular hydrogen atom. We use Newton's law e2 v2 2 = mµ (1) 4π0r r F ma | {z } and the Bohr quantization condition | {z } L = mµvr = n~; (2) where n = 1; 2 · · · . Eliminating v in the first equation and plugging in the second we can find r 2 4π0~ 2 rn = 2 n : (3) mµe The energy in each orbit can be found by 2 2 2 2 mµv e mµ e 1 mµ hydrogen En = − = − 2 2 = En ≈ 200 × (−13:6 eV ) ≈ −2:72keV; (4) 2 4π0r 2~ 4π0 n me where in the last step we restrict ourselves to the n = 1 case. Note that, in the calculation above, we assume that the nucleus does not move. Due to the difference in the masses of the proton and electron (mp ≈ 2000me) that was an excellent approximation for the hydrogen atom. here, the difference between the proton and muon mass is not so large so this approximation is not so good. ii) Is the muon non-relativistic in the ground state of the muonic hydrogen ? The rest mass of the muon is about 200 × me ≈ 200 × 500 keV , which is much larger than the binding (or kinetic) energy of the muon in the muonic hydrogen. The muon is as non-relativistic here and the electron is in the hydrogen atom (there are, however relativistic corrections to the hydrogen spectrum and they are easily measured). iii) What is the wavelength of a photon emitted in a transition between the first excited state and the ground state ? Which kind of photon is it ( radio, microwave, visible, ultraviolet, X-ray, γ-ray, ...) ? The energy of the photon equals the difference in energy between the ground and first excited state 1 1 E = 2:72keV ( − ) ≈ 2:04keV: (5) γ 12 22 Using E = hν and λ = c/ν we find the wavelength to be hc λ = ≈ 0:6 nm; (6) E which is in the X-ray region. iv) Besides the mass, muons differ from electron by the fact that they \decay" into an electron and two massless, chargeless particles called \neutrinos". The lifetime for the decay is about 2 × 10−6s. Does the muon have the time to orbit the proton several times before decaying when it is in the ground state of muonic hydrogen ? The time it takes for the muon to go around one orbit is T = r=v. From 3 we find that v = n~=(mµr) so, for the ground state we have 2 2 3 −15 r m r 4π0~c 1 ~ 4:13=2π × 10 eV:s − T = = µ = ≈ (137)2 ≈ 6 × 10 15s >> muon lifetime: (7) ~ 2 ~2 2 6 eV 2 v e c mµ 1 × 10 c2 c 1/α2 | {z } 2 B. Operator wizardry i) Show that the operator p^ = −i~d=dx is an hermitian operator. 1 1 1 ∗ d d ∗ d ∗ hfjp^jgi = dx f (x)(−i~ )g(x) = dx (i~ f (x))g(x) = dx (−i~ f(x)) g(x) = hpf^ jgi: (8) Z−∞ dx Z−∞ dx Z−∞ dx ii) Compute − y ^ e i ~ pf(x): (9) Hint: expand the exponential and remember the Taylor series expression. − y ^ y 1 y 2 e i ~ pf(x) = (1 − i p^ + (−i p^) + · · · )f(x) (10) ~ 2! ~ d 1 d = (1 − y + (−y )2 + · · · )f(x) (11) dx 2! dx 0 1 00 = f(x) − yf (x) + y2f (x) + · · · (12) 2! = f(x − y): (13) ^ iii) Show that Ψ(x; t) = e−iHt=~Ψ(x; 0) satisfies the Schr¨odinger equation. It is said that p^ generates space transla- tions (from item ii) and H^ generates time translations (by item iii). ^ 1 −iHt n d − ^ ~ d ( ) i~ e iHt= Ψ(x; 0) = i~ ~ Ψ(x; 0) (14) dt dt n! nX=0 1 ^ ( −iHt )n−1 = nH^ ~ Ψ(x; 0) (15) n! nX=1 1 ^ 0 ( −iHt )n = H^ ~ Ψ(x; 0) (16) n0! nX0=0 − ^ ~ = H^ e iHt= Ψ(x; 0): (17).
Load more

Recommended publications
  • The Particle Zoo
    219 8 The Particle Zoo 8.1 Introduction Around 1960 the situation in particle physics was very confusing. Elementary particlesa such as the photon, electron, muon and neutrino were known, but in addition many more particles were being discovered and almost any experiment added more to the list. The main property that these new particles had in common was that they were strongly interacting, meaning that they would interact strongly with protons and neutrons. In this they were different from photons, electrons, muons and neutrinos. A muon may actually traverse a nucleus without disturbing it, and a neutrino, being electrically neutral, may go through huge amounts of matter without any interaction. In other words, in some vague way these new particles seemed to belong to the same group of by Dr. Horst Wahl on 08/28/12. For personal use only. particles as the proton and neutron. In those days proton and neutron were mysterious as well, they seemed to be complicated compound states. At some point a classification scheme for all these particles including proton and neutron was introduced, and once that was done the situation clarified considerably. In that Facts And Mysteries In Elementary Particle Physics Downloaded from www.worldscientific.com era theoretical particle physics was dominated by Gell-Mann, who contributed enormously to that process of systematization and clarification. The result of this massive amount of experimental and theoretical work was the introduction of quarks, and the understanding that all those ‘new’ particles as well as the proton aWe call a particle elementary if we do not know of a further substructure.
    [Show full text]
  • The Five Common Particles
    The Five Common Particles The world around you consists of only three particles: protons, neutrons, and electrons. Protons and neutrons form the nuclei of atoms, and electrons glue everything together and create chemicals and materials. Along with the photon and the neutrino, these particles are essentially the only ones that exist in our solar system, because all the other subatomic particles have half-lives of typically 10-9 second or less, and vanish almost the instant they are created by nuclear reactions in the Sun, etc. Particles interact via the four fundamental forces of nature. Some basic properties of these forces are summarized below. (Other aspects of the fundamental forces are also discussed in the Summary of Particle Physics document on this web site.) Force Range Common Particles It Affects Conserved Quantity gravity infinite neutron, proton, electron, neutrino, photon mass-energy electromagnetic infinite proton, electron, photon charge -14 strong nuclear force ≈ 10 m neutron, proton baryon number -15 weak nuclear force ≈ 10 m neutron, proton, electron, neutrino lepton number Every particle in nature has specific values of all four of the conserved quantities associated with each force. The values for the five common particles are: Particle Rest Mass1 Charge2 Baryon # Lepton # proton 938.3 MeV/c2 +1 e +1 0 neutron 939.6 MeV/c2 0 +1 0 electron 0.511 MeV/c2 -1 e 0 +1 neutrino ≈ 1 eV/c2 0 0 +1 photon 0 eV/c2 0 0 0 1) MeV = mega-electron-volt = 106 eV. It is customary in particle physics to measure the mass of a particle in terms of how much energy it would represent if it were converted via E = mc2.
    [Show full text]
  • Identical Particles
    8.06 Spring 2016 Lecture Notes 4. Identical particles Aram Harrow Last updated: May 19, 2016 Contents 1 Fermions and Bosons 1 1.1 Introduction and two-particle systems .......................... 1 1.2 N particles ......................................... 3 1.3 Non-interacting particles .................................. 5 1.4 Non-zero temperature ................................... 7 1.5 Composite particles .................................... 7 1.6 Emergence of distinguishability .............................. 9 2 Degenerate Fermi gas 10 2.1 Electrons in a box ..................................... 10 2.2 White dwarves ....................................... 12 2.3 Electrons in a periodic potential ............................. 16 3 Charged particles in a magnetic field 21 3.1 The Pauli Hamiltonian ................................... 21 3.2 Landau levels ........................................ 23 3.3 The de Haas-van Alphen effect .............................. 24 3.4 Integer Quantum Hall Effect ............................... 27 3.5 Aharonov-Bohm Effect ................................... 33 1 Fermions and Bosons 1.1 Introduction and two-particle systems Previously we have discussed multiple-particle systems using the tensor-product formalism (cf. Section 1.2 of Chapter 3 of these notes). But this applies only to distinguishable particles. In reality, all known particles are indistinguishable. In the coming lectures, we will explore the mathematical and physical consequences of this. First, consider classical many-particle systems. If a single particle has state described by position and momentum (~r; p~), then the state of N distinguishable particles can be written as (~r1; p~1; ~r2; p~2;:::; ~rN ; p~N ). The notation (·; ·;:::; ·) denotes an ordered list, in which different posi­ tions have different meanings; e.g. in general (~r1; p~1; ~r2; p~2)6 = (~r2; p~2; ~r1; p~1). 1 To describe indistinguishable particles, we can use set notation.
    [Show full text]
  • Muon Decay 1
    Muon Decay 1 LIFETIME OF THE MUON Introduction Muons are unstable particles; otherwise, they are rather like electrons but with much higher masses, approximately 105 MeV. Radioactive nuclear decays do not release enough energy to produce them; however, they are readily available in the laboratory as the dominant component of the cosmic ray flux at the earth’s surface. There are two types of muons, with opposite charge, and they decay into electrons or positrons and two neutrinos according to the rules + + µ → e νe ν¯µ − − µ → e ν¯e νµ . The muon decay is a radioactiveprocess which follows the usual exponential law for the probability of survival for a given time t. Be sure that you understand the basis for this law. The goal of the experiment is to measure the muon lifetime which is roughly 2 µs. With care you can make the measurement with an accuracy of a few percent or better. In order to achieve this goal in a conceptually simple way, we look only at those muons that happen to come to rest inside our detector. That is, we first capture a muon and then measure the elapsed time until it decays. Muons are rather penetrating particles, they can easily go through meters of concrete. Nevertheless, a small fraction of the muons will be slowed down and stopped in the detector. As shown in Figure 1, the apparatus consists of two types of detectors. There is a tank filled with liquid scintillator (a big metal box) viewed by two photomultiplier tubes (Left and Right) and two plastic scintillation counters (flat panels wrapped in black tape), each viewed by a photomul- tiplier tube (Top and Bottom).
    [Show full text]
  • Muon Neutrino Mass Without Oscillations
    The Distant Possibility of Using a High-Luminosity Muon Source to Measure the Mass of the Neutrino Independent of Flavor Oscillations By John Michael Williams [email protected] Markanix Co. P. O. Box 2697 Redwood City, CA 94064 2001 February 19 (v. 1.02) Abstract: Short-baseline calculations reveal that if the neutrino were massive, it would show a beautifully structured spectrum in the energy difference between storage ring and detector; however, this spectrum seems beyond current experimental reach. An interval-timing paradigm would not seem feasible in a short-baseline experiment; however, interval timing on an Earth-Moon long baseline experiment might be able to improve current upper limits on the neutrino mass. Introduction After the Kamiokande and IMB proton-decay detectors unexpectedly recorded neutrinos (probably electron antineutrinos) arriving from the 1987A supernova, a plethora of papers issued on how to use this happy event to estimate the mass of the neutrino. Many of the estimates based on these data put an upper limit on the mass of the electron neutrino of perhaps 10 eV c2 [1]. When Super-Kamiokande and other instruments confirmed the apparent deficit in electron neutrinos from the Sun, and when a deficit in atmospheric muon- neutrinos likewise was observed, this prompted the extension of the kaon-oscillation theory to neutrinos, culminating in a flavor-oscillation theory based by analogy on the CKM quark mixing matrix. The oscillation theory was sensitive enough to provide evidence of a neutrino mass, even given the low statistics available at the largest instruments. J. M. Williams Neutrino Mass Without Oscillations (2001-02-19) 2 However, there is reason to doubt that the CKM analysis validly can be applied physically over the long, nonvirtual propagation distances of neutrinos [2].
    [Show full text]
  • Quantum Mechanics
    Quantum Mechanics Richard Fitzpatrick Professor of Physics The University of Texas at Austin Contents 1 Introduction 5 1.1 Intendedaudience................................ 5 1.2 MajorSources .................................. 5 1.3 AimofCourse .................................. 6 1.4 OutlineofCourse ................................ 6 2 Probability Theory 7 2.1 Introduction ................................... 7 2.2 WhatisProbability?.............................. 7 2.3 CombiningProbabilities. ... 7 2.4 Mean,Variance,andStandardDeviation . ..... 9 2.5 ContinuousProbabilityDistributions. ........ 11 3 Wave-Particle Duality 13 3.1 Introduction ................................... 13 3.2 Wavefunctions.................................. 13 3.3 PlaneWaves ................................... 14 3.4 RepresentationofWavesviaComplexFunctions . ....... 15 3.5 ClassicalLightWaves ............................. 18 3.6 PhotoelectricEffect ............................. 19 3.7 QuantumTheoryofLight. .. .. .. .. .. .. .. .. .. .. .. .. .. 21 3.8 ClassicalInterferenceofLightWaves . ...... 21 3.9 QuantumInterferenceofLight . 22 3.10 ClassicalParticles . .. .. .. .. .. .. .. .. .. .. .. .. .. .. 25 3.11 QuantumParticles............................... 25 3.12 WavePackets .................................. 26 2 QUANTUM MECHANICS 3.13 EvolutionofWavePackets . 29 3.14 Heisenberg’sUncertaintyPrinciple . ........ 32 3.15 Schr¨odinger’sEquation . 35 3.16 CollapseoftheWaveFunction . 36 4 Fundamentals of Quantum Mechanics 39 4.1 Introduction ..................................
    [Show full text]
  • Proton Therapy ACKNOWLEDGEMENTS
    AMERICAN BRAIN TUMOR ASSOCIATION Proton Therapy ACKNOWLEDGEMENTS ABOUT THE AMERICAN BRAIN TUMOR ASSOCIATION Founded in 1973, the American Brain Tumor Association (ABTA) was the first national nonprofit organization dedicated solely to brain tumor research. For over 40 years, the Chicago-based ABTA has been providing comprehensive resources that support the complex needs of brain tumor patients and caregivers, as well as the critical funding of research in the pursuit of breakthroughs in brain tumor diagnosis, treatment and care. To learn more about the ABTA, visit www.abta.org. We gratefully acknowledge Anita Mahajan, Director of International Development, MD Anderson Proton Therapy Center, director, Pediatric Radiation Oncology, co-section head of Pediatric and CNS Radiation Oncology, The University of Texas MD Anderson Cancer Center; Kevin S. Oh, MD, Department of Radiation Oncology, Massachusetts General Hospital; and Sridhar Nimmagadda, PhD, assistant professor of Radiology, Medicine and Oncology, Johns Hopkins University, for their review of this edition of this publication. This publication is not intended as a substitute for professional medical advice and does not provide advice on treatments or conditions for individual patients. All health and treatment decisions must be made in consultation with your physician(s), utilizing your specific medical information. Inclusion in this publication is not a recommendation of any product, treatment, physician or hospital. COPYRIGHT © 2015 ABTA REPRODUCTION WITHOUT PRIOR WRITTEN PERMISSION IS PROHIBITED AMERICAN BRAIN TUMOR ASSOCIATION Proton Therapy INTRODUCTION Brain tumors are highly variable in their treatment and prognosis. Many are benign and treated conservatively, while others are malignant and require aggressive combinations of surgery, radiation and chemotherapy.
    [Show full text]
  • On the Possibility of Generating a 4-Neutron Resonance with a {\Boldmath $ T= 3/2$} Isospin 3-Neutron Force
    On the possibility of generating a 4-neutron resonance with a T = 3/2 isospin 3-neutron force E. Hiyama Nishina Center for Accelerator-Based Science, RIKEN, Wako, 351-0198, Japan R. Lazauskas IPHC, IN2P3-CNRS/Universite Louis Pasteur BP 28, F-67037 Strasbourg Cedex 2, France J. Carbonell Institut de Physique Nucl´eaire, Universit´eParis-Sud, IN2P3-CNRS, 91406 Orsay Cedex, France M. Kamimura Department of Physics, Kyushu University, Fukuoka 812-8581, Japan and Nishina Center for Accelerator-Based Science, RIKEN, Wako 351-0198, Japan (Dated: September 26, 2018) We consider the theoretical possibility to generate a narrow resonance in the four neutron system as suggested by a recent experimental result. To that end, a phenomenological T = 3/2 three neutron force is introduced, in addition to a realistic NN interaction. We inquire what should be the strength of the 3n force in order to generate such a resonance. The reliability of the three-neutron force in the T = 3/2 channel is exmined, by analyzing its consistency with the low-lying T = 1 states of 4H, 4He and 4Li and the 3H+ n scattering. The ab initio solution of the 4n Schr¨odinger equation is obtained using the complex scaling method with boundary conditions appropiate to the four-body resonances. We find that in order to generate narrow 4n resonant states a remarkably attractive 3N force in the T = 3/2 channel is required. I. INTRODUCTION ergy axis (physical domain) it will have no significant impact on a physical process. The possibility of detecting a four-neutron (4n) structure of Following this line of reasoning, some calculations based any kind – bound or resonant state – has intrigued the nuclear on semi-realistic NN forces indicated null [13] or unlikely physics community for the last fifty years (see Refs.
    [Show full text]
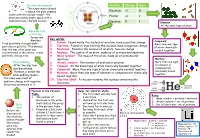
  • Key Words: 1. Proton: Found Inside the Nucleus of an Atom, Have a Positive Charge 2. Electron: Found in Rings Orbiting the Nucle
    Nucleus development Particle Charge Mass This experiment allowed Rutherford to replace the plum pudding Electron -1 0 model with the nuclear model – the Proton +1 1 atom was mainly empty space with a small positively charged nucleus Neutron 0 1 Element All the same type of atom Alpha particle scattering Geiger and Key words: Marsden 1. Proton: Found inside the nucleus of an atom, have a positive charge Compound fired positively-charged alpha More than one type 2. Electron: Found in rings orbiting the nucleus, have a negative charge particles at gold foil. This showed of atom chemically that the mas of an atom was 3. Neutrons: Found in the nucleus of an atom, have no charge bonded together concentrated in the centre, it was 4. Nucleus: The centre of an atom, made up of protons and neutrons positively charged too 5. Mass number: The mass of the atom, made up of protons and neutrons Mixture Plum pudding 6. Atomic number: The number of protons in an atom More than one type After the electron 7. Element: All the same type of atom chemically bonded together of element or was discovered, 8. Compound: More than one type of atom chemically bonded together compound not chemically bound Thomson created the 9. Mixture: More than one type of element or compound not chemically together plum pudding model – bound together the atom was a ball of 10. Electron Shell: A ring surrounding the nucleus containing the positive charge with negative electrons electrons scattered in it Position in the Periodic Rules for electron shells: Table: 1.
    [Show full text]
  • TO the POSSIBILITY of BOUND STATES BETWEEN TWO ELECTRONS Alexander A
    WEPPP031 Proceedings of IPAC2012, New Orleans, Louisiana, USA TO THE POSSIBILITY OF BOUND STATES BETWEEN TWO ELECTRONS Alexander A. Mikhailichenko, Cornell University, LEPP, Ithaca, NY 14853, USA Abstract spins for reduction of minimal emittance restriction arisen from Eq. 1. In some sense it is an attempt to prepare the We analyze the possibility to compress dynamically the pure quantum mechanical state between just two polarized electron bunch so that the distance between electrons. What is important here is that the distance some electrons in the bunch comes close to the Compton between two electrons should be of the order of the wavelength, arranging a bound state, as the attraction by Compton wavelength. We attracted attention in [2,3] that the magnetic momentum-induced force at this distance attraction between two electrons determined by the dominates repulsion by the electrostatic force for the magnetic force of oppositely oriented magnetic moments. appropriately prepared orientation of the magnetic In this case the resulting spin is zero. Another possibility moments of the electron-electron pair. This electron pair considered below. behaves like a boson now, so the restriction for the In [4], it was suggested a radical explanation of minimal emittance of the beam becomes eliminated. structure of all elementary particles caused by magnetic Some properties of such degenerated electron gas attraction at the distances of the order of Compton represented also. wavelength. In [5], motion of charged particle in a field OVERVIEW of magnetic dipole was considered. In [4] and [5] the term in Hamiltonian responsible for the interaction Generation of beams of particles (electrons, positrons, between magnetic moments is omitted, however as it protons, muons) with minimal emittance is a challenging looks like problem in contemporary beam physics.
    [Show full text]
  • Muons: Particles of the Moment
    FEATURES Measurements of the anomalous magnetic moment of the muon provide strong hints that the Standard Model of particle physics might be incomplete Muons: particles of the moment David W Hertzog WHEN asked what the most important strange, bottom and top; and six leptons, issue in particle physics is today, my ABORATORY namely the electron, muon and tau- colleagues offer three burning ques- L lepton plus their associated neutrinos. ATIONAL tions: What is the origin of mass? Why N A different set of particles is respon- is the universe made of matter and not sible for the interactions between these equal parts of matter and antimatter? ROOKHAVEN matter particles in the model. The elec- And is there any physics beyond the B tromagnetic interaction that binds elec- Standard Model? trons to nuclei results from the exchange The first question is being addressed of photons, whereas the strong force by a feverish quest to find the Higgs that binds quarks together inside neut- boson, which is believed to be respon- rons, protons and other hadrons is car- sible for the mass of fundamental par- ried by particles called gluons. The ticles. The Tevatron at Fermilab, which third force in the Standard Model – the is currently running, or the Large Had- weak nuclear interaction, which is re- ron Collider at CERN, which is due sponsible for radioactive decay – is car- to start experiments in 2007, should OWMAN ried by the W and Z bosons. B IPP eventually provide the answer to this R Physicists love the Standard Model, question by detecting the Higgs and but they do not like it.
    [Show full text]
  • Detection of a Strange Particle
    10 extraordinary papers Within days, Watson and Crick had built a identify the full set of codons was completed in forensics, and research into more-futuristic new model of DNA from metal parts. Wilkins by 1966, with Har Gobind Khorana contributing applications, such as DNA-based computing, immediately accepted that it was correct. It the sequences of bases in several codons from is well advanced. was agreed between the two groups that they his experiments with synthetic polynucleotides Paradoxically, Watson and Crick’s iconic would publish three papers simultaneously in (see go.nature.com/2hebk3k). structure has also made it possible to recog- Nature, with the King’s researchers comment- With Fred Sanger and colleagues’ publica- nize the shortcomings of the central dogma, ing on the fit of Watson and Crick’s structure tion16 of an efficient method for sequencing with the discovery of small RNAs that can reg- to the experimental data, and Franklin and DNA in 1977, the way was open for the com- ulate gene expression, and of environmental Gosling publishing Photograph 51 for the plete reading of the genetic information in factors that induce heritable epigenetic first time7,8. any species. The task was completed for the change. No doubt, the concept of the double The Cambridge pair acknowledged in their human genome by 2003, another milestone helix will continue to underpin discoveries in paper that they knew of “the general nature in the history of DNA. biology for decades to come. of the unpublished experimental results and Watson devoted most of the rest of his ideas” of the King’s workers, but it wasn’t until career to education and scientific administra- Georgina Ferry is a science writer based in The Double Helix, Watson’s explosive account tion as head of the Cold Spring Harbor Labo- Oxford, UK.
    [Show full text]