DOCSLIB.ORG

Quantum Mechanics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Quantum Mechanics Quantum Mechanics Richard Fitzpatrick Professor of Physics The University of Texas at Austin Contents 1 Introduction 5 1.1 Intendedaudience................................ 5 1.2 MajorSources .................................. 5 1.3 AimofCourse .................................. 6 1.4 OutlineofCourse ................................ 6 2 Probability Theory 7 2.1 Introduction ................................... 7 2.2 WhatisProbability?.............................. 7 2.3 CombiningProbabilities. ... 7 2.4 Mean,Variance,andStandardDeviation . ..... 9 2.5 ContinuousProbabilityDistributions. ........ 11 3 Wave-Particle Duality 13 3.1 Introduction ................................... 13 3.2 Wavefunctions.................................. 13 3.3 PlaneWaves ................................... 14 3.4 RepresentationofWavesviaComplexFunctions . ....... 15 3.5 ClassicalLightWaves ............................. 18 3.6 PhotoelectricEffect ............................. 19 3.7 QuantumTheoryofLight. .. .. .. .. .. .. .. .. .. .. .. .. .. 21 3.8 ClassicalInterferenceofLightWaves . ...... 21 3.9 QuantumInterferenceofLight . 22 3.10 ClassicalParticles . .. .. .. .. .. .. .. .. .. .. .. .. .. .. 25 3.11 QuantumParticles............................... 25 3.12 WavePackets .................................. 26 2 QUANTUM MECHANICS 3.13 EvolutionofWavePackets . 29 3.14 Heisenberg’sUncertaintyPrinciple . ........ 32 3.15 Schr¨odinger’sEquation . 35 3.16 CollapseoftheWaveFunction . 36 4 Fundamentals of Quantum Mechanics 39 4.1 Introduction ................................... 39 4.2 Schr¨odinger’sEquation . 39 4.3 NormalizationoftheWavefunction . 39 4.4 ExpectationValuesandVariances . 42 4.5 Ehrenfest’sTheorem.............................. 43 4.6 Operators .................................... 45 4.7 MomentumRepresentation. 47 4.8 Heisenberg’sUncertaintyPrinciple . ....... 50 4.9 EigenstatesandEigenvalues . 53 4.10 Measurement .................................. 56 4.11 ContinuousEigenvalues. 57 4.12 StationaryStates ............................... 60 5 One-Dimensional Potentials 63 5.1 Introduction ................................... 63 5.2 InfinitePotentialWell . .. .. .. .. .. .. .. .. .. .. .. .. .. 63 5.3 SquarePotentialBarrier. 64 5.4 WKBApproximation .............................. 70 5.5 ColdEmission .................................. 72 5.6 AlphaDecay ................................... 73 5.7 SquarePotentialWell ............................. 75 5.8 SimpleHarmonicOscillator . 80 6 Multi-Particle Systems 85 6.1 Introduction ................................... 85 6.2 FundamentalConcepts ............................. 85 6.3 Non-InteractingParticles . 86 6.4 Two-ParticleSystems ............................. 88 6.5 IdenticalParticles .............................. 89 7 Three-Dimensional Quantum Mechanics 93 7.1 Introduction ................................... 93 7.2 FundamentalConcepts ............................. 93 7.3 ParticleinaBox................................. 96 7.4 DegenerateElectronGases . 97 7.5 White-DwarfStars................................ 100 CONTENTS 3 8 Orbital Angular Momentum 103 8.1 Introduction ...................................103 8.2 AngularMomentumOperators. 103 8.3 RepresentationofAngularMomentum . 105 8.4 EigenstatesofAngularMomentum. 106 8.5 Eigenvalues of Lz ................................107 8.6 Eigenvalues of L2 ................................108 8.7 SphericalHarmonics .............................. 110 9 Central Potentials 115 9.1 Introduction ...................................115 9.2 DerivationofRadialEquation . 115 9.3 InfiniteSphericalPotentialWell . 118 9.4 HydrogenAtom .................................121 9.5 RydbergFormula ................................126 10 Spin Angular Momentum 129 10.1 Introduction ................................... 129 10.2 SpinOperators.................................. 129 10.3 SpinSpace....................................130 2 10.4 Eigenstates of Sz and S .............................131 10.5 PauliRepresentation . 133 10.6 SpinPrecession ................................. 136 11 Addition of Angular Momentum 141 11.1 Introduction ................................... 141 11.2 GeneralPrinciples. .. .. .. .. .. .. .. .. .. .. .. .. .. .. 141 11.3 AngularMomentumintheHydrogenAtom . 144 11.4 TwoSpinOne-HalfParticles . 147 12 Time-Independent Perturbation Theory 151 12.1 Introduction ................................... 151 12.2 ImprovedNotation ............................... 151 12.3 Two-StateSystem ................................ 153 12.4 Non-DegeneratePerturbationTheory . 155 12.5 QuadraticStarkEffect. 156 12.6 DegeneratePerturbationTheory . 160 12.7 LinearStarkEffect. .. .. .. .. .. .. .. .. .. .. .. .. .. .. 163 12.8 FineStructureofHydrogen. 164 12.9 ZeemanEffect ..................................169 12.10HyperfineStructure . 170 13 Time-Dependent Perturbation Theory 175 4 QUANTUM MECHANICS 13.1 Introduction ................................... 175 13.2 PreliminaryAnalysis. 175 13.3 Two-StateSystem ................................ 177 13.4 SpinMagneticResonance. 178 13.5 PerturbationExpansion . 180 13.6 HarmonicPerturbations. 181 13.7 ElectromagneticRadiation . 183 13.8 ElectricDipoleApproximation . 186 13.9 SpontaneousEmission . 188 13.10 RadiationfromaHarmonicOscillator . .......190 13.11SelectionRules ................................ 191 13.12 2P 1S TransitionsinHydrogen . 192 13.13IntensityRules................................ 194 13.14ForbiddenTransitions→ . 194 14 Variational Methods 197 14.1 Introduction ................................... 197 14.2 VariationalPrinciple. 197 14.3 HeliumAtom ..................................199 14.4 HydrogenMoleculeIon. 204 15 Scattering Theory 209 15.1 Introduction ................................... 209 15.2 Fundamentals ..................................209 15.3 BornApproximation.. .. .. .. .. .. .. .. .. .. .. .. .. .. .. 211 15.4 PartialWaves ..................................213 15.5 DeterminationofPhase-Shifts . 216 15.6 HardSphereScattering . 217 15.7 LowEnergyScattering . 219 15.8 Resonances....................................220 Introduction 5 1 Introduction 1.1 Intended audience These lecture notes outline a single semester course on non-relativistic quantum mechanics which is primarily intended for upper-division undergraduate physics majors. The course assumes some previous knowledge of physics and mathematics. In particular, prospective students should be reasonably familiar with Newtonian dynamics, elementary classical electromagnetism and special relativity, the physics and mathematics of waves (includ- ing the representation of waves via complex functions), basic probability theory, ordinary and partial differential equations, linear algebra, vector algebra, and Fourier series and transforms. 1.2 Major Sources The textbooks which I have consulted most frequently whilst developing course material are: The Principles of Quantum Mechanics, P.A.M. Dirac, 4th Edition (revised), (Oxford Univer- sity Press, Oxford UK, 1958). Quantum Mechanics, E. Merzbacher, 2nd Edition, (John Wiley & Sons, New York NY, 1970). Introduction to the Quantum Theory, D. Park, 2nd Edition, (McGraw-Hill, New York NY, 1974). Modern Quantum Mechanics, J.J. Sakurai, (Benjamin/Cummings, Menlo Park CA, 1985). Quantum Theory, D. Bohm, (Dover, New York NY, 1989). Problems in Quantum Mechanics, G.L. Squires, (Cambridge University Press, Cambridge UK, 1995). Quantum Physics, S. Gasiorowicz, 2nd Edition, (John Wiley & Sons, New York NY, 1996). Nonclassical Physics, R. Harris, (Addison-Wesley, Menlo Park CA, 1998). Introduction to Quantum Mechanics, D.J. Griffiths, 2nd Edition, (Pearson Prentice Hall, Upper Saddle River NJ, 2005). 6 QUANTUM MECHANICS 1.3 Aim of Course The aim of this course is to develop non-relativistic quantum mechanics as a complete theory of microscopic dynamics, capable of making detailed predictions, with a minimum of abstract mathematics. 1.4 Outline of Course The first part of the course is devoted to an in-depth exploration of the basic principles of quantum mechanics. After a brief review of probability theory, in Chapter 2, we shall start, in Chapter 3, by examining how many of the central ideas of quantum mechanics are a direct consequence of wave-particle duality—i.e., the concept that waves sometimes act as particles, and particles as waves. We shall then proceed to investigate the rules of quantum mechanics in a more systematic fashion in Chapter 4. Quantum mechanics is used to examine the motion of a single particle in one dimension, many particles in one dimension, and a single particle in three dimensions, in Chapters 5, 6, and 7, respectively. Chapter 8 is devoted to the investigation of orbital angular momentum, and Chapter 9 to the closely related subject of particle motion in a central potential. Finally, in Chapters 10 and 11, we shall examine spin angular momentum, and the addition of orbital and spin angular momentum, respectively. The second part of this course describes selected practical applications of quantum mechanics. In Chapter 12, time-independent perturbation theory is used to investigate the Stark effect, the Zeeman effect, fine structure, and hyperfine structure, in the hydrogen atom. Time-dependent perturbation theory is employed to study radiative transitions in the hydrogen atom in Chapter 13. Chapter 14 illustrates the use of variational methods in quantum mechanics. Finally, Chapter 15 contains an introduction to quantum scattering theory. Probability Theory 7 2 Probability Theory 2.1 Introduction This section is devoted
Load more

Recommended publications
  • The Particle Zoo
    219 8 The Particle Zoo 8.1 Introduction Around 1960 the situation in particle physics was very confusing. Elementary particlesa such as the photon, electron, muon and neutrino were known, but in addition many more particles were being discovered and almost any experiment added more to the list. The main property that these new particles had in common was that they were strongly interacting, meaning that they would interact strongly with protons and neutrons. In this they were different from photons, electrons, muons and neutrinos. A muon may actually traverse a nucleus without disturbing it, and a neutrino, being electrically neutral, may go through huge amounts of matter without any interaction. In other words, in some vague way these new particles seemed to belong to the same group of by Dr. Horst Wahl on 08/28/12. For personal use only. particles as the proton and neutron. In those days proton and neutron were mysterious as well, they seemed to be complicated compound states. At some point a classification scheme for all these particles including proton and neutron was introduced, and once that was done the situation clarified considerably. In that Facts And Mysteries In Elementary Particle Physics Downloaded from www.worldscientific.com era theoretical particle physics was dominated by Gell-Mann, who contributed enormously to that process of systematization and clarification. The result of this massive amount of experimental and theoretical work was the introduction of quarks, and the understanding that all those ‘new’ particles as well as the proton aWe call a particle elementary if we do not know of a further substructure.
    [Show full text]
  • Lecture 32 Relevant Sections in Text: §3.7, 3.9 Total Angular Momentum
    Physics 6210/Spring 2008/Lecture 32 Lecture 32 Relevant sections in text: x3.7, 3.9 Total Angular Momentum Eigenvectors How are the total angular momentum eigenvectors related to the original product eigenvectors (eigenvectors of Lz and Sz)? We will sketch the construction and give the results. Keep in mind that the general theory of angular momentum tells us that, for a 1 given l, there are only two values for j, namely, j = l ± 2. Begin with the eigenvectors of total angular momentum with the maximum value of angular momentum: 1 1 1 jj = l; j = ; j = l + ; m = l + i: 1 2 2 2 j 2 Given j1 and j2, there is only one linearly independent eigenvector which has the appro- priate eigenvalue for Jz, namely 1 1 jj = l; j = ; m = l; m = i; 1 2 2 1 2 2 so we have 1 1 1 1 1 jj = l; j = ; j = l + ; m = l + i = jj = l; j = ; m = l; m = i: 1 2 2 2 2 1 2 2 1 2 2 To get the eigenvectors with lower eigenvalues of Jz we can apply the ladder operator J− = L− + S− to this ket and normalize it. In this way we get expressions for all the kets 1 1 1 1 1 jj = l; j = 1=2; j = l + ; m i; m = −l − ; −l + ; : : : ; l − ; l + : 1 2 2 j j 2 2 2 2 The details can be found in the text. 1 1 Next, we consider j = l − 2 for which the maximum mj value is mj = l − 2.
    [Show full text]
  • Path Integrals in Quantum Mechanics
    Path Integrals in Quantum Mechanics Dennis V. Perepelitsa MIT Department of Physics 70 Amherst Ave. Cambridge, MA 02142 Abstract We present the path integral formulation of quantum mechanics and demon- strate its equivalence to the Schr¨odinger picture. We apply the method to the free particle and quantum harmonic oscillator, investigate the Euclidean path integral, and discuss other applications. 1 Introduction A fundamental question in quantum mechanics is how does the state of a particle evolve with time? That is, the determination the time-evolution ψ(t) of some initial | i state ψ(t ) . Quantum mechanics is fully predictive [3] in the sense that initial | 0 i conditions and knowledge of the potential occupied by the particle is enough to fully specify the state of the particle for all future times.1 In the early twentieth century, Erwin Schr¨odinger derived an equation specifies how the instantaneous change in the wavefunction d ψ(t) depends on the system dt | i inhabited by the state in the form of the Hamiltonian. In this formulation, the eigenstates of the Hamiltonian play an important role, since their time-evolution is easy to calculate (i.e. they are stationary). A well-established method of solution, after the entire eigenspectrum of Hˆ is known, is to decompose the initial state into this eigenbasis, apply time evolution to each and then reassemble the eigenstates. That is, 1In the analysis below, we consider only the position of a particle, and not any other quantum property such as spin. 2 D.V. Perepelitsa n=∞ ψ(t) = exp [ iE t/~] n ψ(t ) n (1) | i − n h | 0 i| i n=0 X This (Hamiltonian) formulation works in many cases.
    [Show full text]
  • Key Concepts for Future QIS Learners Workshop Output Published Online May 13, 2020
    Key Concepts for Future QIS Learners Workshop output published online May 13, 2020 Background and Overview On behalf of the Interagency Working Group on Workforce, Industry and Infrastructure, under the NSTC Subcommittee on Quantum Information Science (QIS), the National Science Foundation invited 25 researchers and educators to come together to deliberate on defining a core set of key concepts for future QIS learners that could provide a starting point for further curricular and educator development activities. The deliberative group included university and industry researchers, secondary school and college educators, and representatives from educational and professional organizations. The workshop participants focused on identifying concepts that could, with additional supporting resources, help prepare secondary school students to engage with QIS and provide possible pathways for broader public engagement. This workshop report identifies a set of nine Key Concepts. Each Concept is introduced with a concise overall statement, followed by a few important fundamentals. Connections to current and future technologies are included, providing relevance and context. The first Key Concept defines the field as a whole. Concepts 2-6 introduce ideas that are necessary for building an understanding of quantum information science and its applications. Concepts 7-9 provide short explanations of critical areas of study within QIS: quantum computing, quantum communication and quantum sensing. The Key Concepts are not intended to be an introductory guide to quantum information science, but rather provide a framework for future expansion and adaptation for students at different levels in computer science, mathematics, physics, and chemistry courses. As such, it is expected that educators and other community stakeholders may not yet have a working knowledge of content covered in the Key Concepts.
    [Show full text]
  • Identical Particles
    8.06 Spring 2016 Lecture Notes 4. Identical particles Aram Harrow Last updated: May 19, 2016 Contents 1 Fermions and Bosons 1 1.1 Introduction and two-particle systems .......................... 1 1.2 N particles ......................................... 3 1.3 Non-interacting particles .................................. 5 1.4 Non-zero temperature ................................... 7 1.5 Composite particles .................................... 7 1.6 Emergence of distinguishability .............................. 9 2 Degenerate Fermi gas 10 2.1 Electrons in a box ..................................... 10 2.2 White dwarves ....................................... 12 2.3 Electrons in a periodic potential ............................. 16 3 Charged particles in a magnetic field 21 3.1 The Pauli Hamiltonian ................................... 21 3.2 Landau levels ........................................ 23 3.3 The de Haas-van Alphen effect .............................. 24 3.4 Integer Quantum Hall Effect ............................... 27 3.5 Aharonov-Bohm Effect ................................... 33 1 Fermions and Bosons 1.1 Introduction and two-particle systems Previously we have discussed multiple-particle systems using the tensor-product formalism (cf. Section 1.2 of Chapter 3 of these notes). But this applies only to distinguishable particles. In reality, all known particles are indistinguishable. In the coming lectures, we will explore the mathematical and physical consequences of this. First, consider classical many-particle systems. If a single particle has state described by position and momentum (~r; p~), then the state of N distinguishable particles can be written as (~r1; p~1; ~r2; p~2;:::; ~rN ; p~N ). The notation (·; ·;:::; ·) denotes an ordered list, in which different posi­ tions have different meanings; e.g. in general (~r1; p~1; ~r2; p~2)6 = (~r2; p~2; ~r1; p~1). 1 To describe indistinguishable particles, we can use set notation.
    [Show full text]
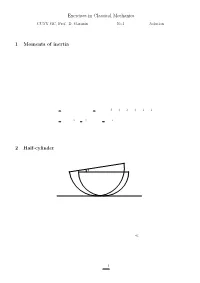
  • Exercises in Classical Mechanics 1 Moments of Inertia 2 Half-Cylinder
    Exercises in Classical Mechanics CUNY GC, Prof. D. Garanin No.1 Solution ||||||||||||||||||||||||||||||||||||||||| 1 Moments of inertia (5 points) Calculate tensors of inertia with respect to the principal axes of the following bodies: a) Hollow sphere of mass M and radius R: b) Cone of the height h and radius of the base R; both with respect to the apex and to the center of mass. c) Body of a box shape with sides a; b; and c: Solution: a) By symmetry for the sphere I®¯ = I±®¯: (1) One can ¯nd I easily noticing that for the hollow sphere is 1 1 X ³ ´ I = (I + I + I ) = m y2 + z2 + z2 + x2 + x2 + y2 3 xx yy zz 3 i i i i i i i i 2 X 2 X 2 = m r2 = R2 m = MR2: (2) 3 i i 3 i 3 i i b) and c): Standard solutions 2 Half-cylinder ϕ (10 points) Consider a half-cylinder of mass M and radius R on a horizontal plane. a) Find the position of its center of mass (CM) and the moment of inertia with respect to CM. b) Write down the Lagrange function in terms of the angle ' (see Fig.) c) Find the frequency of cylinder's oscillations in the linear regime, ' ¿ 1. Solution: (a) First we ¯nd the distance a between the CM and the geometrical center of the cylinder. With σ being the density for the cross-sectional surface, so that ¼R2 M = σ ; (3) 2 1 one obtains Z Z 2 2σ R p σ R q a = dx x R2 ¡ x2 = dy R2 ¡ y M 0 M 0 ¯ 2 ³ ´3=2¯R σ 2 2 ¯ σ 2 3 4 = ¡ R ¡ y ¯ = R = R: (4) M 3 0 M 3 3¼ The moment of inertia of the half-cylinder with respect to the geometrical center is the same as that of the cylinder, 1 I0 = MR2: (5) 2 The moment of inertia with respect to the CM I can be found from the relation I0 = I + Ma2 (6) that yields " µ ¶ # " # 1 4 2 1 32 I = I0 ¡ Ma2 = MR2 ¡ = MR2 1 ¡ ' 0:3199MR2: (7) 2 3¼ 2 (3¼)2 (b) The Lagrange function L is given by L('; '_ ) = T ('; '_ ) ¡ U('): (8) The potential energy U of the half-cylinder is due to the elevation of its CM resulting from the deviation of ' from zero.
    [Show full text]
  • Singlet NMR Methodology in Two-Spin-1/2 Systems
    Singlet NMR Methodology in Two-Spin-1/2 Systems Giuseppe Pileio School of Chemistry, University of Southampton, SO17 1BJ, UK The author dedicates this work to Prof. Malcolm H. Levitt on the occasion of his 60th birthaday Abstract This paper discusses methodology developed over the past 12 years in order to access and manipulate singlet order in systems comprising two coupled spin- 1/2 nuclei in liquid-state nuclear magnetic resonance. Pulse sequences that are valid for different regimes are discussed, and fully analytical proofs are given using different spin dynamics techniques that include product operator methods, the single transition operator formalism, and average Hamiltonian theory. Methods used to filter singlet order from byproducts of pulse sequences are also listed and discussed analytically. The theoretical maximum amplitudes of the transformations achieved by these techniques are reported, together with the results of numerical simulations performed using custom-built simulation code. Keywords: Singlet States, Singlet Order, Field-Cycling, Singlet-Locking, M2S, SLIC, Singlet Order filtration Contents 1 Introduction 2 2 Nuclear Singlet States and Singlet Order 4 2.1 The spin Hamiltonian and its eigenstates . 4 2.2 Population operators and spin order . 6 2.3 Maximum transformation amplitude . 7 2.4 Spin Hamiltonian in single transition operator formalism . 8 2.5 Relaxation properties of singlet order . 9 2.5.1 Coherent dynamics . 9 2.5.2 Incoherent dynamics . 9 2.5.3 Central relaxation property of singlet order . 10 2.6 Singlet order and magnetic equivalence . 11 3 Methods for manipulating singlet order in spin-1/2 pairs 13 3.1 Field Cycling .
    [Show full text]
  • Toward Quantum Simulation with Rydberg Atoms Thanh Long Nguyen
    Study of dipole-dipole interaction between Rydberg atoms : toward quantum simulation with Rydberg atoms Thanh Long Nguyen To cite this version: Thanh Long Nguyen. Study of dipole-dipole interaction between Rydberg atoms : toward quantum simulation with Rydberg atoms. Physics [physics]. Université Pierre et Marie Curie - Paris VI, 2016. English. NNT : 2016PA066695. tel-01609840 HAL Id: tel-01609840 https://tel.archives-ouvertes.fr/tel-01609840 Submitted on 4 Oct 2017 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. DÉPARTEMENT DE PHYSIQUE DE L’ÉCOLE NORMALE SUPÉRIEURE LABORATOIRE KASTLER BROSSEL THÈSE DE DOCTORAT DE L’UNIVERSITÉ PIERRE ET MARIE CURIE Spécialité : PHYSIQUE QUANTIQUE Study of dipole-dipole interaction between Rydberg atoms Toward quantum simulation with Rydberg atoms présentée par Thanh Long NGUYEN pour obtenir le grade de DOCTEUR DE L’UNIVERSITÉ PIERRE ET MARIE CURIE Soutenue le 18/11/2016 devant le jury composé de : Dr. Michel BRUNE Directeur de thèse Dr. Thierry LAHAYE Rapporteur Pr. Shannon WHITLOCK Rapporteur Dr. Bruno LABURTHE-TOLRA Examinateur Pr. Jonathan HOME Examinateur Pr. Agnès MAITRE Examinateur To my parents and my brother To my wife and my daughter ii Acknowledgement “Voici mon secret.
    [Show full text]
  • The Statistical Interpretation of Entangled States B
    The Statistical Interpretation of Entangled States B. C. Sanctuary Department of Chemistry, McGill University 801 Sherbrooke Street W Montreal, PQ, H3A 2K6, Canada Abstract Entangled EPR spin pairs can be treated using the statistical ensemble interpretation of quantum mechanics. As such the singlet state results from an ensemble of spin pairs each with an arbitrary axis of quantization. This axis acts as a quantum mechanical hidden variable. If the spins lose coherence they disentangle into a mixed state. Whether or not the EPR spin pairs retain entanglement or disentangle, however, the statistical ensemble interpretation resolves the EPR paradox and gives a mechanism for quantum “teleportation” without the need for instantaneous action-at-a-distance. Keywords: Statistical ensemble, entanglement, disentanglement, quantum correlations, EPR paradox, Bell’s inequalities, quantum non-locality and locality, coincidence detection 1. Introduction The fundamental questions of quantum mechanics (QM) are rooted in the philosophical interpretation of the wave function1. At the time these were first debated, covering the fifty or so years following the formulation of QM, the arguments were based primarily on gedanken experiments2. Today the situation has changed with numerous experiments now possible that can guide us in our search for the true nature of the microscopic world, and how The Infamous Boundary3 to the macroscopic world is breached. The current view is based upon pivotal experiments, performed by Aspect4 showing that quantum mechanics is correct and Bell’s inequalities5 are violated. From this the non-local nature of QM became firmly entrenched in physics leading to other experiments, notably those demonstrating that non-locally is fundamental to quantum “teleportation”.
    [Show full text]
  • The Hydrogen Atom (Finite Difference Equation/Discrete Wave Vectors/Bohr-Rydberg Formula) FREDERICK T
    Proc. Natl. Acad. Sci. USA Vol. 83, pp. 5753-5755, August 1986 Chemistry Discrete wave mechanics: The hydrogen atom (finite difference equation/discrete wave vectors/Bohr-Rydberg formula) FREDERICK T. WALL Department of Chemistry, B-017, University of California at San Diego, La Jolla, CA 92093 Contributed by Frederick T. Wall, March 31, 1986 ABSTRACT The quantum mechanical problem of the hy- its wave vector energy counterpart.* If V is small compared drogen atom is treated by use of a finite difference equation in to mc2, then V and l9 are substantially the same, but for large place of Schrodinger's differential equation. The exact solu- negative values of V, the two can be significantly different. tion leads to a wave vector energy expression that is readily The next question to be answered is how the potential en- converted to the Bohr-Rydberg formula. (The calculations ergy is introduced into the finite difference equation. In our here reported are limited to spherically symmetric states.) The problem, we shall write that wave vectors reduce to the familiar solutions of Schrodinger's equation as c -- w. The internal consistency and limiting be- O(r - A) - 2(X + V/mc2)4(r) + /(r + A) = 0, [2] havior provide support for the view that the equations em- ployed could well constitute an approach to a relativistic for- with mulation of wave mechanics. X = = (1 - 26/E)"2 [3] In an earlier paper (1), I set forth a simple difference equa- EI/E tion for the wave mechanical description of a free particle. This was accompanied by a postulatory basis for interpreting where & is the wave vector energy, and certain parameters related to the energy, thus appearing to provide a possible connection to relativity.
    [Show full text]
  • Note to 8.13 Students
    Note to 8.13 students: Feel free to look at this paper for some suggestions about the lab, but please reference/acknowledge me as if you had read my report or spoken to me in person. Also note that this is only one way to do the lab and data analysis, and there are nearly an infinite number of other things to do that would be better. I made some mistakes doing this lab. Here are a couple I found (and some more tips): Use a smaller step and get more precise data than what we had. Then fit • a curve, don’t just pick out a peak. The Hg calibration is actually something like a sin wave instead of a cubic. • Also don’t follow the old version of Melissionos word for word. They use an optical system with a prism oppose to a diffraction grating. We took data strategically so we could use unweighted fits • The mystery tube was actually N, whoops my bad. We later found a • drawer full of tubes and compared the colors. It was obviously N. Again whoops, it was our first experiment okay?! 1 Optical Spectroscopy Rachel Bowens-Rubin∗ MIT Department of Physics (Dated: July 12, 2010) The spectra of mercury, hydrogen, deuterium, sodium, and an unidentified mystery tube were measured using a monochromator to determine diffrent properties of their spectra. The spectrum of mercury was used to calibrate for error due to optics in the monochronomator. The measurements of the Balmer series lines were used to determine the Rydberg constants for hydrogen and deuterium, 7 7 1 7 7 1 Rh =1.0966 10 0.0002 10 m− and Rd=1.0970 10 0.0003 10 m− .
    [Show full text]
  • Quantum Mechanics for Beginners OUP CORRECTED PROOF – FINAL, 10/3/2020, Spi OUP CORRECTED PROOF – FINAL, 10/3/2020, Spi
    OUP CORRECTED PROOF – FINAL, 10/3/2020, SPi Quantum Mechanics for Beginners OUP CORRECTED PROOF – FINAL, 10/3/2020, SPi OUP CORRECTED PROOF – FINAL, 10/3/2020, SPi Quantum Mechanics for Beginners with applications to quantum communication and quantum computing M. Suhail Zubairy Texas A&M University 1 OUP CORRECTED PROOF – FINAL, 10/3/2020, SPi 3 Great Clarendon Street, Oxford, OX2 6DP, United Kingdom Oxford University Press is a department of the University of Oxford. It furthers the University’s objective of excellence in research, scholarship, and education by publishing worldwide. Oxford is a registered trade mark of Oxford University Press in the UK and in certain other countries © M. Suhail Zubairy 2020 The moral rights of the author have been asserted First Edition published in 2020 Impression: 1 All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, without the prior permission in writing of Oxford University Press, or as expressly permitted by law, by licence or under terms agreed with the appropriate reprographics rights organization. Enquiries concerning reproduction outside the scope of the above should be sent to the Rights Department, Oxford University Press, at the address above You must not circulate this work in any other form and you must impose this same condition on any acquirer Published in the United States of America by Oxford University Press 198 Madison Avenue, New York, NY 10016, United States of America British Library Cataloguing
    [Show full text]