DOCSLIB.ORG

Charm and Strange Quark Contributions to the Proton Structure

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Charm and Strange Quark Contributions to the Proton Structure Report series ISSN 0284 - 2769 of SE9900247 THE SVEDBERG LABORATORY and \ DEPARTMENT OF RADIATION SCIENCES UPPSALA UNIVERSITY Box 533, S-75121 Uppsala, Sweden http://www.tsl.uu.se/ TSL/ISV-99-0204 February 1999 Charm and Strange Quark Contributions to the Proton Structure Kristel Torokoff1 Dept. of Radiation Sciences, Uppsala University, Box 535, S-751 21 Uppsala, Sweden Abstract: The possibility to have charm and strange quarks as quantum mechanical fluc- tuations in the proton wave function is investigated based on a model for non-perturbative QCD dynamics. Both hadron and parton basis are examined. A scheme for energy fluctu- ations is constructed and compared with explicit energy-momentum conservation. Resulting momentum distributions for charniand_strange quarks in the proton are derived at the start- ing scale Qo f°r the perturbative QCD evolution. Kinematical constraints are found to be important when comparing to the "intrinsic charm" model. Master of Science Thesis Linkoping University Supervisor: Gunnar Ingelman, Uppsala University 1 kuldsepp@tsl .uu.se 30-37 Contents 1 Introduction 1 2 Standard Model 3 2.1 Introductory QCD 4 2.2 Light-cone variables 5 3 Experiments 7 3.1 The HERA machine 7 3.2 Deep Inelastic Scattering 8 4 Theory 11 4.1 The Parton model 11 4.2 The structure functions 12 4.3 Perturbative QCD corrections 13 4.4 The DGLAP equations 14 5 The Edin-Ingelman Model 15 6 Heavy Quarks in the Proton Wave Function 19 6.1 Extrinsic charm 19 6.2 Intrinsic charm 20 6.3 Hadronisation 22 6.4 The El-model applied to heavy quarks 23 6.4.1 The hadron basis 24 6.4.2 The parton basis 25 7 Energy Fluctuation in Hadron Basis 25 7.1 Kinematics 26 7.2 Detailed description of the method 28 7.3 Constraints 29 8 Energy Fluctuation in Parton Basis 30 8.1 Kinematics 30 8.2 Constraints 31 9 Energy Conservation in Hadron Basis 31 9.1 Kinematics 31 9.2 Constraints 33 10 Energy Conservation in Parton Basis 33 10.1 Kinematics 33 10.2 Constraints 34 11 The Momentum Fraction x and Bjorken Scaling Variable XB 34 11.1 General definition of x and XB 34 11.2 The relationship of x and XB in the methods 35 12 Overview of the Methods 36 12.1 The method with energy fluctuation 36 12.2 The method with energy conservation 37 13 Results on Charm 37 13.1 Internal model quantities 37 13.2 Charm quark momentum distributions 39 14 Discussion 41 14.1 The credibility of the methods 41 14.2 The capability of the methods 43 15 Strangeness 44 16 Results on Strange Quarks 45 16.1 Internal model quantities 45 16.2 Strange quark momentum distributions 45 16.3 Discussion 46 17 Conclusions 47 "I ca'n't believe that}" said Alice. "Ca'n't you?" the Queen said in a pitying tone. "Try again: draw a long breath, and shut your eyes." Alice laughed. "There is no use trying," she said, "one ca'n't believe impossible things." "I daresay you haven't had much practice," said the Queen. Why, sometimes I've believed as many as six impossible things before breakfast." Lewis Carroll 1 Introduction The first experimental evidence that the proton has an internal structure was obtained in 1969 at Stanford Linear Accelerator Center (SLAC) [1]. Since then many high energy physics experiments have been performed and shown that the proton is a bound state of quarks. The valence quarks (two up and one down quark) give the proton its characteristic quantum numbers. A new theory of strong interactions, Quantum ChromoDynamics (QCD), has been developed, where the interaction between quarks is mediated by the field quanta called gluons. The proton, once thought to be a simple pointlike particle is found to have a complex internal structure. As a quantum mechanical particle, the proton may fluctuate in any way as long as its quantum numbers are conserved. Described in a hadron basis the proton may fluctuate into a baryon (a three quark bound state) and a meson (a bound state of a quark and an anti-quark), in parton basis additional quark anti-quark pairs are considered. The life-time of a fluctuation is given by the Heisenberg uncertainty relation, At ~ -^. Thus, the smaller the mass of the fluctuation, the longer the life-time and thereby the larger the probability of having such a fluctuation. In general these probability amplitudes are unknown. Naturally the fluctuations into light particles should be dominant due to the low mass, but in principle there may also exist fluctuations into heavy particles, even including charm. The problem is rather how to describe these fluctuations. All these fluctuations are part of the total proton wave function. Unfortunately this wave function is largely unknown. It cannot be derived from first principles because of the complex non-perturbative internal dynamics of the proton. Experiments give merely limited information because only one parton is probed at a time. In this way the wave function can be partially represented by momentum distributions of partons, i.e. quarks and gluons in the proton. These distributions provide the probabilities of scattering on a certain quark or gluon. They are conventionally obtained by fitting parametrisations to experimental data. A model to derive these distributions from non-perturbative dynamics was presented by Edin and Ingelman [3]. The El-model is based on quantum mechanical fluctuations. The valence parton distributions were derived from partonic fluctuations in the proton while the additional partons were assumed to originate from hadronic fluctuations of the proton. For a long time it was a common belief that only the massless or approximately massless partons (gluons, up and down quarks) may be part of the proton wave function. Heavy quarks were treated as "extrinsic", i.e. generated by large-momentum processes described by perturbative QCD. The conventional mechanism for charm production is the photon-gluon- fusion (PGF) process photon + gluon -> charm + anticharm. However there are experimental data which are in conflict with the predictions of the PGF model. Contrary to expectations, charm quarks have been found to also carry larger fractions of the proton's momentum [10], and charmed particles have been observed closer to the proton beam direction [11]. These data indicate an additional source of charm production. This has led to a model with "intrinsic" heavy quarks in the proton [9]. The model has been studied for over 15 years, but has still not been neither confirmed nor ruled out. As a further investigation of this problem, this thesis develops the El-model to be applicable also for heavy quark fluctuations in the proton. This includes a careful analysis of suitable quantum mechanical bases and treatment of energy fluctuations. The report is organised as follows. In Section 2 background material in terms of the Standard Model and the strong interaction are reviewed based on books such as those in [2]. The natural units are used throughout this thesis, i.e. c = h = I. The internal structure of the proton is best studied in deep inelastic electron-proton scattering experiments, as discussed in Section 3, and with theoretical aspects treated in Section 4. The El-model is described in Section 5. In Section 6 alternative descriptions of charm and strange quarks in the proton are discussed. The new approaches derived from the El-model are described and applied to charmed fluctuations in Sections 7 to 10 and to strange fluctuations in Section 15. A detailed treatment of the momentum fraction x is given in Section 11. The methods are summarised and compared in block diagrams in Section 12. The resulting charm momentum distributions are presented in Section 13, followed by a critical discussion of methods and results in Section 14. Similarly, the case of strangeness is discussed in 16. Finally, Section 17 gives a concluding discussion. 2 Standard Model The Standard Model (SM) is the theoretical framework which describes the elementary parti- cles and their interactions as known today. The theory is mathematically self-consistent but has 19 parameters that must be determined from data. Yet, no experimental result in conflict with the model has been found. In SM the fundamental particles are the leptons and the quarks. Up to the present limits of resolution, ~ 10~18m, they are known to be structureless. They can be arranged into three generations of increasing mass, as shown in Table 1. Flavour Mass Electric Flavour Mass Electric Flavour Mass Electric GeV charge GeV charge GeV charge u ~ 0.005 2/3 c ~ 1.4 2/3 t ~170 2/3 d ~0.01 -1/3 s ~0.2 -1/3 b ~4.7 -1/3 e 0.000511 -1 0.106 -1 T 1.7771 -1 9 < 7 x 10~ 0 < 0.0003 0 Vr <0.03 0 Table 1: The elementary particles in Standard Model The six types of quarks, the flavours, are called up, down, charm, strange, top and bottom. In addition to the electric charge they also carry colour, which is the charge of the strong interaction. There are three different colour charges, conventionally labelled as red, green and blue. Each charged lepton, i.e. electron, muon and taon, has a neutrino associated with it. For each of these particles there exists a corresponding anti-particle with opposite sign of many quantum numbers. The fundamental interactions in the SM are shortly summarised in Table 2. Interaction Field Basic coupling Couplings Range 2 quanta Quarks Leptons atQ 0 2^y Y^ Electromagnetic (EM) photon 7 A A a « 10~2 oo ± /d /e 18 Weak Z°,W oew ~ ID 10- m Strong gluons g a « 1 10-15m Table 2: The fundamental interactions and some of their properties.
Load more

Recommended publications
  • The Five Common Particles
    The Five Common Particles The world around you consists of only three particles: protons, neutrons, and electrons. Protons and neutrons form the nuclei of atoms, and electrons glue everything together and create chemicals and materials. Along with the photon and the neutrino, these particles are essentially the only ones that exist in our solar system, because all the other subatomic particles have half-lives of typically 10-9 second or less, and vanish almost the instant they are created by nuclear reactions in the Sun, etc. Particles interact via the four fundamental forces of nature. Some basic properties of these forces are summarized below. (Other aspects of the fundamental forces are also discussed in the Summary of Particle Physics document on this web site.) Force Range Common Particles It Affects Conserved Quantity gravity infinite neutron, proton, electron, neutrino, photon mass-energy electromagnetic infinite proton, electron, photon charge -14 strong nuclear force ≈ 10 m neutron, proton baryon number -15 weak nuclear force ≈ 10 m neutron, proton, electron, neutrino lepton number Every particle in nature has specific values of all four of the conserved quantities associated with each force. The values for the five common particles are: Particle Rest Mass1 Charge2 Baryon # Lepton # proton 938.3 MeV/c2 +1 e +1 0 neutron 939.6 MeV/c2 0 +1 0 electron 0.511 MeV/c2 -1 e 0 +1 neutrino ≈ 1 eV/c2 0 0 +1 photon 0 eV/c2 0 0 0 1) MeV = mega-electron-volt = 106 eV. It is customary in particle physics to measure the mass of a particle in terms of how much energy it would represent if it were converted via E = mc2.
    [Show full text]
  • The Particle World
    The Particle World ² What is our Universe made of? This talk: ² Where does it come from? ² particles as we understand them now ² Why does it behave the way it does? (the Standard Model) Particle physics tries to answer these ² prepare you for the exercise questions. Later: future of particle physics. JMF Southampton Masterclass 22–23 Mar 2004 1/26 Beginning of the 20th century: atoms have a nucleus and a surrounding cloud of electrons. The electrons are responsible for almost all behaviour of matter: ² emission of light ² electricity and magnetism ² electronics ² chemistry ² mechanical properties . technology. JMF Southampton Masterclass 22–23 Mar 2004 2/26 Nucleus at the centre of the atom: tiny Subsequently, particle physicists have yet contains almost all the mass of the discovered four more types of quark, two atom. Yet, it’s composite, made up of more pairs of heavier copies of the up protons and neutrons (or nucleons). and down: Open up a nucleon . it contains ² c or charm quark, charge +2=3 quarks. ² s or strange quark, charge ¡1=3 Normal matter can be understood with ² t or top quark, charge +2=3 just two types of quark. ² b or bottom quark, charge ¡1=3 ² + u or up quark, charge 2=3 Existed only in the early stages of the ² ¡ d or down quark, charge 1=3 universe and nowadays created in high energy physics experiments. JMF Southampton Masterclass 22–23 Mar 2004 3/26 But this is not all. The electron has a friend the electron-neutrino, ºe. Needed to ensure energy and momentum are conserved in ¯-decay: ¡ n ! p + e + º¯e Neutrino: no electric charge, (almost) no mass, hardly interacts at all.
    [Show full text]
  • Qcd in Heavy Quark Production and Decay
    QCD IN HEAVY QUARK PRODUCTION AND DECAY Jim Wiss* University of Illinois Urbana, IL 61801 ABSTRACT I discuss how QCD is used to understand the physics of heavy quark production and decay dynamics. My discussion of production dynam- ics primarily concentrates on charm photoproduction data which is compared to perturbative QCD calculations which incorporate frag- mentation effects. We begin our discussion of heavy quark decay by reviewing data on charm and beauty lifetimes. Present data on fully leptonic and semileptonic charm decay is then reviewed. Mea- surements of the hadronic weak current form factors are compared to the nonperturbative QCD-based predictions of Lattice Gauge The- ories. We next discuss polarization phenomena present in charmed baryon decay. Heavy Quark Effective Theory predicts that the daugh- ter baryon will recoil from the charmed parent with nearly 100% left- handed polarization, which is in excellent agreement with present data. We conclude by discussing nonleptonic charm decay which are tradi- tionally analyzed in a factorization framework applicable to two-body and quasi-two-body nonleptonic decays. This discussion emphasizes the important role of final state interactions in influencing both the observed decay width of various two-body final states as well as mod- ifying the interference between Interfering resonance channels which contribute to specific multibody decays. "Supported by DOE Contract DE-FG0201ER40677. © 1996 by Jim Wiss. -251- 1 Introduction the direction of fixed-target experiments. Perhaps they serve as a sort of swan song since the future of fixed-target charm experiments in the United States is A vast amount of important data on heavy quark production and decay exists for very short.
    [Show full text]
  • Higgs and Particle Production in Nucleus-Nucleus Collisions
    Higgs and Particle Production in Nucleus-Nucleus Collisions Zhe Liu Submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy in the Graduate School of Arts and Sciences Columbia University 2016 c 2015 Zhe Liu All Rights Reserved Abstract Higgs and Particle Production in Nucleus-Nucleus Collisions Zhe Liu We apply a diagrammatic approach to study Higgs boson, a color-neutral heavy particle, pro- duction in nucleus-nucleus collisions in the saturation framework without quantum evolution. We assume the strong coupling constant much smaller than one. Due to the heavy mass and colorless nature of Higgs particle, final state interactions are absent in our calculation. In order to treat the two nuclei dynamically symmetric, we use the Coulomb gauge which gives the appropriate light cone gauge for each nucleus. To further eliminate initial state interactions we choose specific prescriptions in the light cone propagators. We start the calculation from only two nucleons in each nucleus and then demonstrate how to generalize the calculation to higher orders diagrammatically. We simplify the diagrams by the Slavnov-Taylor-Ward identities. The resulting cross section is factorized into a product of two Weizsäcker-Williams gluon distributions of the two nuclei when the transverse momentum of the produced scalar particle is around the saturation momentum. To our knowledge this is the first process where an exact analytic formula has been formed for a physical process, involving momenta on the order of the saturation momentum, in nucleus-nucleus collisions in the quasi-classical approximation. Since we have performed the calculation in an unconventional gauge choice, we further confirm our results in Feynman gauge where the Weizsäcker-Williams gluon distribution is interpreted as a transverse momentum broadening of a hard gluons traversing a nuclear medium.
    [Show full text]
  • Baryon Number Fluctuation and the Quark-Gluon Plasma
    Baryon Number Fluctuation and the Quark-Gluon Plasma Z. W. Lin and C. M. Ko Because of the fractional baryon number Using the generating function at of quarks, baryon and antibaryon number equilibrium, fluctuations in the quark-gluon plasma is less than those in the hadronic matter, making them plausible signatures for the quark-gluon plasma expected to be formed in relativistic heavy ion with g(l) = ∑ Pn = 1 due to normalization of collisions. To illustrate this possibility, we have the multiplicity probability distribution, it is introduced a kinetic model that takes into straightforward to obtain all moments of the account both production and annihilation of equilibrium multiplicity distribution. In terms of quark-antiquark or baryon-antibaryon pairs [1]. the fundamental unit of baryon number bo in the In the case of only baryon-antibaryon matter, the mean baryon number per event is production from and annihilation to two mesons, given by i.e., m1m2 ↔ BB , we have the following master equation for the multiplicity distribution of BB pairs: while the squared baryon number fluctuation per baryon at equilibrium is given by In obtaining the last expressions in Eqs. (5) and In the above, Pn(ϑ) denotes the probability of ϑ 〈σ 〉 (6), we have kept only the leading term in E finding n pairs of BB at time ; G ≡ G v 〈σ 〉 corresponding to the grand canonical limit, and L ≡ L v are the momentum-averaged cross sections for baryon production and E 1, as baryons and antibaryons are abundantly produced in heavy ion collisions at annihilation, respectively; Nk represents the total number of particle species k; and V is the proper RHIC.
    [Show full text]
  • Particle Physics Dr Victoria Martin, Spring Semester 2012 Lecture 12: Hadron Decays
    Particle Physics Dr Victoria Martin, Spring Semester 2012 Lecture 12: Hadron Decays !Resonances !Heavy Meson and Baryons !Decays and Quantum numbers !CKM matrix 1 Announcements •No lecture on Friday. •Remaining lectures: •Tuesday 13 March •Friday 16 March •Tuesday 20 March •Friday 23 March •Tuesday 27 March •Friday 30 March •Tuesday 3 April •Remaining Tutorials: •Monday 26 March •Monday 2 April 2 From Friday: Mesons and Baryons Summary • Quarks are confined to colourless bound states, collectively known as hadrons: " mesons: quark and anti-quark. Bosons (s=0, 1) with a symmetric colour wavefunction. " baryons: three quarks. Fermions (s=1/2, 3/2) with antisymmetric colour wavefunction. " anti-baryons: three anti-quarks. • Lightest mesons & baryons described by isospin (I, I3), strangeness (S) and hypercharge Y " isospin I=! for u and d quarks; (isospin combined as for spin) " I3=+! (isospin up) for up quarks; I3="! (isospin down) for down quarks " S=+1 for strange quarks (additive quantum number) " hypercharge Y = S + B • Hadrons display SU(3) flavour symmetry between u d and s quarks. Used to predict the allowed meson and baryon states. • As baryons are fermions, the overall wavefunction must be anti-symmetric. The wavefunction is product of colour, flavour, spin and spatial parts: ! = "c "f "S "L an odd number of these must be anti-symmetric. • consequences: no uuu, ddd or sss baryons with total spin J=# (S=#, L=0) • Residual strong force interactions between colourless hadrons propagated by mesons. 3 Resonances • Hadrons which decay due to the strong force have very short lifetime # ~ 10"24 s • Evidence for the existence of these states are resonances in the experimental data Γ2/4 σ = σ • Shape is Breit-Wigner distribution: max (E M)2 + Γ2/4 14 41.
    [Show full text]
  • Arxiv:1502.07763V2 [Hep-Ph] 1 Apr 2015
    Constraints on Dark Photon from Neutrino-Electron Scattering Experiments S. Bilmi¸s,1 I. Turan,1 T.M. Aliev,1 M. Deniz,2, 3 L. Singh,2, 4 and H.T. Wong2 1Department of Physics, Middle East Technical University, Ankara 06531, Turkey. 2Institute of Physics, Academia Sinica, Taipei 11529, Taiwan. 3Department of Physics, Dokuz Eyl¨ulUniversity, Izmir,_ Turkey. 4Department of Physics, Banaras Hindu University, Varanasi, 221005, India. (Dated: April 2, 2015) Abstract A possible manifestation of an additional light gauge boson A0, named as Dark Photon, associated with a group U(1)B−L is studied in neutrino electron scattering experiments. The exclusion plot on the coupling constant gB−L and the dark photon mass MA0 is obtained. It is shown that contributions of interference term between the dark photon and the Standard Model are important. The interference effects are studied and compared with for data sets from TEXONO, GEMMA, BOREXINO, LSND as well as CHARM II experiments. Our results provide more stringent bounds to some regions of parameter space. PACS numbers: 13.15.+g,12.60.+i,14.70.Pw arXiv:1502.07763v2 [hep-ph] 1 Apr 2015 1 CONTENTS I. Introduction 2 II. Hidden Sector as a beyond the Standard Model Scenario 3 III. Neutrino-Electron Scattering 6 A. Standard Model Expressions 6 B. Very Light Vector Boson Contributions 7 IV. Experimental Constraints 9 A. Neutrino-Electron Scattering Experiments 9 B. Roles of Interference 13 C. Results 14 V. Conclusions 17 Acknowledgments 19 References 20 I. INTRODUCTION The recent discovery of the Standard Model (SM) long-sought Higgs at the Large Hadron Collider is the last missing piece of the SM which is strengthened its success even further.
    [Show full text]
  • Fully Strange Tetraquark Sss¯S¯ Spectrum and Possible Experimental Evidence
    PHYSICAL REVIEW D 103, 016016 (2021) Fully strange tetraquark sss¯s¯ spectrum and possible experimental evidence † Feng-Xiao Liu ,1,2 Ming-Sheng Liu,1,2 Xian-Hui Zhong,1,2,* and Qiang Zhao3,4,2, 1Department of Physics, Hunan Normal University, and Key Laboratory of Low-Dimensional Quantum Structures and Quantum Control of Ministry of Education, Changsha 410081, China 2Synergetic Innovation Center for Quantum Effects and Applications (SICQEA), Hunan Normal University, Changsha 410081, China 3Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China 4University of Chinese Academy of Sciences, Beijing 100049, China (Received 21 August 2020; accepted 5 January 2021; published 26 January 2021) In this work, we construct 36 tetraquark configurations for the 1S-, 1P-, and 2S-wave states, and make a prediction of the mass spectrum for the tetraquark sss¯s¯ system in the framework of a nonrelativistic potential quark model without the diquark-antidiquark approximation. The model parameters are well determined by our previous study of the strangeonium spectrum. We find that the resonances f0ð2200Þ and 2340 2218 2378 f2ð Þ may favor the assignments of ground states Tðsss¯s¯Þ0þþ ð Þ and Tðsss¯s¯Þ2þþ ð Þ, respectively, and the newly observed Xð2500Þ at BESIII may be a candidate of the lowest mass 1P-wave 0−þ state − 2481 0þþ 2440 Tðsss¯s¯Þ0 þ ð Þ. Signals for the other ground state Tðsss¯s¯Þ0þþ ð Þ may also have been observed in PC −− the ϕϕ invariant mass spectrum in J=ψ → γϕϕ at BESIII. The masses of the J ¼ 1 Tsss¯s¯ states are predicted to be in the range of ∼2.44–2.99 GeV, which indicates that the ϕð2170Þ resonance may not be a good candidate of the Tsss¯s¯ state.
    [Show full text]
  • Arxiv:0810.4453V1 [Hep-Ph] 24 Oct 2008
    The Physics of Glueballs Vincent Mathieu Groupe de Physique Nucl´eaire Th´eorique, Universit´e de Mons-Hainaut, Acad´emie universitaire Wallonie-Bruxelles, Place du Parc 20, BE-7000 Mons, Belgium. [email protected] Nikolai Kochelev Bogoliubov Laboratory of Theoretical Physics, Joint Institute for Nuclear Research, Dubna, Moscow region, 141980 Russia. [email protected] Vicente Vento Departament de F´ısica Te`orica and Institut de F´ısica Corpuscular, Universitat de Val`encia-CSIC, E-46100 Burjassot (Valencia), Spain. [email protected] Glueballs are particles whose valence degrees of freedom are gluons and therefore in their descrip- tion the gauge field plays a dominant role. We review recent results in the physics of glueballs with the aim set on phenomenology and discuss the possibility of finding them in conventional hadronic experiments and in the Quark Gluon Plasma. In order to describe their properties we resort to a va- riety of theoretical treatments which include, lattice QCD, constituent models, AdS/QCD methods, and QCD sum rules. The review is supposed to be an informed guide to the literature. Therefore, we do not discuss in detail technical developments but refer the reader to the appropriate references. I. INTRODUCTION Quantum Chromodynamics (QCD) is the theory of the hadronic interactions. It is an elegant theory whose full non perturbative solution has escaped our knowledge since its formulation more than 30 years ago.[1] The theory is asymptotically free[2, 3] and confining.[4] A particularly good test of our understanding of the nonperturbative aspects of QCD is to study particles where the gauge field plays a more important dynamical role than in the standard hadrons.
    [Show full text]
  • Proton Therapy ACKNOWLEDGEMENTS
    AMERICAN BRAIN TUMOR ASSOCIATION Proton Therapy ACKNOWLEDGEMENTS ABOUT THE AMERICAN BRAIN TUMOR ASSOCIATION Founded in 1973, the American Brain Tumor Association (ABTA) was the first national nonprofit organization dedicated solely to brain tumor research. For over 40 years, the Chicago-based ABTA has been providing comprehensive resources that support the complex needs of brain tumor patients and caregivers, as well as the critical funding of research in the pursuit of breakthroughs in brain tumor diagnosis, treatment and care. To learn more about the ABTA, visit www.abta.org. We gratefully acknowledge Anita Mahajan, Director of International Development, MD Anderson Proton Therapy Center, director, Pediatric Radiation Oncology, co-section head of Pediatric and CNS Radiation Oncology, The University of Texas MD Anderson Cancer Center; Kevin S. Oh, MD, Department of Radiation Oncology, Massachusetts General Hospital; and Sridhar Nimmagadda, PhD, assistant professor of Radiology, Medicine and Oncology, Johns Hopkins University, for their review of this edition of this publication. This publication is not intended as a substitute for professional medical advice and does not provide advice on treatments or conditions for individual patients. All health and treatment decisions must be made in consultation with your physician(s), utilizing your specific medical information. Inclusion in this publication is not a recommendation of any product, treatment, physician or hospital. COPYRIGHT © 2015 ABTA REPRODUCTION WITHOUT PRIOR WRITTEN PERMISSION IS PROHIBITED AMERICAN BRAIN TUMOR ASSOCIATION Proton Therapy INTRODUCTION Brain tumors are highly variable in their treatment and prognosis. Many are benign and treated conservatively, while others are malignant and require aggressive combinations of surgery, radiation and chemotherapy.
    [Show full text]
  • 11. the Cabibbo-Kobayashi-Maskawa Mixing Matrix
    11. CKM mixing matrix 103 11. THE CABIBBO-KOBAYASHI-MASKAWA MIXING MATRIX Revised 1997 by F.J. Gilman (Carnegie-Mellon University), where ci =cosθi and si =sinθi for i =1,2,3. In the limit K. Kleinknecht and B. Renk (Johannes-Gutenberg Universit¨at θ2 = θ3 = 0, this reduces to the usual Cabibbo mixing with θ1 Mainz). identified (up to a sign) with the Cabibbo angle [2]. Several different forms of the Kobayashi-Maskawa parametrization are found in the In the Standard Model with SU(2) × U(1) as the gauge group of literature. Since all these parametrizations are referred to as “the” electroweak interactions, both the quarks and leptons are assigned to Kobayashi-Maskawa form, some care about which one is being used is be left-handed doublets and right-handed singlets. The quark mass needed when the quadrant in which δ lies is under discussion. eigenstates are not the same as the weak eigenstates, and the matrix relating these bases was defined for six quarks and given an explicit A popular approximation that emphasizes the hierarchy in the size parametrization by Kobayashi and Maskawa [1] in 1973. It generalizes of the angles, s12 s23 s13 , is due to Wolfenstein [4], where one ≡ the four-quark case, where the matrix is parametrized by a single sets λ s12 , the sine of the Cabibbo angle, and then writes the other angle, the Cabibbo angle [2]. elements in terms of powers of λ: × By convention, the mixing is often expressed in terms of a 3 3 1 − λ2/2 λAλ3(ρ−iη) − unitary matrix V operating on the charge e/3 quarks (d, s,andb): V = −λ 1 − λ2/2 Aλ2 .
    [Show full text]
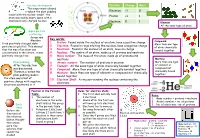
  • Key Words: 1. Proton: Found Inside the Nucleus of an Atom, Have a Positive Charge 2. Electron: Found in Rings Orbiting the Nucle
    Nucleus development Particle Charge Mass This experiment allowed Rutherford to replace the plum pudding Electron -1 0 model with the nuclear model – the Proton +1 1 atom was mainly empty space with a small positively charged nucleus Neutron 0 1 Element All the same type of atom Alpha particle scattering Geiger and Key words: Marsden 1. Proton: Found inside the nucleus of an atom, have a positive charge Compound fired positively-charged alpha More than one type 2. Electron: Found in rings orbiting the nucleus, have a negative charge particles at gold foil. This showed of atom chemically that the mas of an atom was 3. Neutrons: Found in the nucleus of an atom, have no charge bonded together concentrated in the centre, it was 4. Nucleus: The centre of an atom, made up of protons and neutrons positively charged too 5. Mass number: The mass of the atom, made up of protons and neutrons Mixture Plum pudding 6. Atomic number: The number of protons in an atom More than one type After the electron 7. Element: All the same type of atom chemically bonded together of element or was discovered, 8. Compound: More than one type of atom chemically bonded together compound not chemically bound Thomson created the 9. Mixture: More than one type of element or compound not chemically together plum pudding model – bound together the atom was a ball of 10. Electron Shell: A ring surrounding the nucleus containing the positive charge with negative electrons electrons scattered in it Position in the Periodic Rules for electron shells: Table: 1.
    [Show full text]