DOCSLIB.ORG

A Multi-Method Simulation of a High-Frequency Bus Line Using Anylogic

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Multi-Method Simulation of a High-Frequency Bus Line Using Anylogic A multi-method simulation of a high-frequency bus line using AnyLogic Thierry van der Spek Name Two LIACS, Leiden University LIACS, Leiden University [email protected] [email protected] ABSTRACT able approach to visualize this bus line and create a better In this work a mixed agent-based and discrete event simula- comprehension of frequently occurring problems. One of the tion model is developed for a high frequency bus route in the external factors, the number of passengers, is modelled and Netherlands. With this model, different passenger growth can be configured to analyse several passenger growth sce- scenarios can be easily evaluated. This simulation model narios. The effect of these scenarios is illustrated by several helps policy makers to predict changes that have to be made key performance indicators (KPIs), determined by Arriva. to bus routes and planned travel times before problems oc- This paper is structured as follows: In Section 2, common cur. The model is validated using several performance indi- domain terminology is introduced to gain a better under- cators, showing that under some model assumptions, it can standing of the problems occurring. In Section 3, the prob- realistically simulate real-life situations. The simulation's lems occurring are described by formulating our KPIs. In workings are illustrated by two use cases. Section 4, we look into related work in this domain, and also at other agent-based and discrete-event simulation models. 1. INTRODUCTION Section 5 discusses the data that is considered and the data sets that are used. Also, the preprocessing of data that In all metropolitan areas, people rely on buses as a means is needed to generate our model is discussed. Thereafter, of transportation. Commuters increasingly use public trans- in Section 6, the modelling choices that are made are dis- port to get to or go from their work or study location in these cussed. In Section 7, the discussed model is validated using areas. This puts a high strain on bus companies to pro- the defined KPIs and two use cases of passenger growth are vide a reliable and frequent service, especially during rush discussed. Finally, in Section 8, we conclude this work and hours. The procession of buses is easily disrupted by dif- possible future perspectives are briefly discussed. ferent factors such as congestion, traffic lights, open bridges and passengers boarding or alighting. This causes delays, which again may cause bus bunching. Bus bunching, the 2. BACKGROUND INFORMATION uneven spacing of buses over a route, causes uneven load- In this section, we go over some basic definitions that are ing of passengers and therefore inefficient usage of material. needed to gain a better understanding of the problem defini- Furthermore, passenger satisfaction may be lower due to full tion and the proposed model. Furthermore, common charac- buses. teristics for service quality and reliability that the proposed In the Randstad megalopolis in central-western Nether- model provides insight into are defined. lands, several high-frequency bus lines are created to inter- connect cities. Such a high-frequency line provides a quick 2.1 Preliminaries connection between places, but inherently is challenged by In this section, notation needed to define the bus route these disruptive influences. This work aims to create insight and terminology used in the field of public transport are into these factors and their effect on travel time on one of given. Some definitions might be common knowledge, but these high-frequency bus lines between the cities of Leiden others are less known outside this discipline. arXiv:1704.05692v1 [cs.AI] 19 Apr 2017 and Zoetermeer, exploited by the Arriva bus company. A group of bus lines can be seen as a graph G = We show that a combination of agent-based and discrete- (V; E), which is a combination of a set of stops V = 1 event models using the AnyLogic simulation tool are a suit- fv0; v1; v2; : : : ; vng and a set of route segments E ⊆ V × V . A stop vi is a designated place at which passengers can alight 1 Anylogic Multimethod Simulation, http://anylogic.com/, Vis- or board the bus. ited: Feb 17, 2017 We define P to be the set of all possible bus trips: P = fv0; : : : ; vn j 80 ≤ i < n :(vi; vi+1) 2 E; (1) 80 ≤ h < i ≤ n : vh = vi =) (h; i) = (0; n)g A bus trip p 2 P of length n can then be seen as an This student paper is the result of an academic computer science research ordered sequence of n + 1 stops, where there exists a route project. Permission to make digital or hard copies of all or part of this work segment ei 2 E from every stop vi to its subsequent stop for personal or classroom use is granted without fee provided that copies are v . not made or distributed for profit or commercial advantage and that copies i+1 bear this notice on the first page. We call stops v0 and vn terminals. At these stops, the bus changes trips. Figure 1 shows a schematic overview of TTi DTi v0 v1 vi−1 vi vi+1 vn Figure 1: Schematic overview of bus stops along one direction of a bus line with n + 1 stops. The arrow indicates the direction in which the bus is travelling. Dots indicate possible other stops on the route. Stops 0 and n are terminal stops. a trip. they are part of the R-net concept2, which only allows these Between stops, the bus drives these specific route seg- specific buses to drive designated routes. ments. The time that each segment ei takes is called travel To create a reliable bus line there are some important fac- time (TTi). Travel time can be measured between stop de- tors that have to be optimized. In this work, the R-net 400 partures, between departure at stop vi and arrival at stop bus line is simulated, whilst giving insight into some of these vi+1 or vice versa. We define travel time (TTi) between stop factors. Two main components of customer satisfaction are vi−1 and vi as the time between departure at stop vi−1 and waiting time and seat availability [14]. We discuss both of arrival at stop vi, which is the time it takes to travel seg- them below. ment ei. We note that when we talk about travel time, we talk about the time that it takes to travel a route segment Waiting time towards a stop from its preceding stop, therefore e0 is not Waiting time is mainly determined by bus punctuality and defined. regularity. Bus lines can either consist of a single trip in which the start terminal is the same as the end terminal v = v , or 0 n • Punctuality: punctuality is usually seen as being on two trips in roughly opposite directions v0 6= vn. For the first case we have a circular bus line, which is more common time. Punctuality shifts are caused by any deviation in urban areas. In the latter case most bus stops are usually from the scheduled arrival time at a stop. In this in opposite sides of the road to allow passengers to travel in paper, the term punctuality is used as the inverse, both directions of the route. so that an increase in punctuality defines a larger Furthermore, stops are defined by a GPS radius. This deviation from the schedule. This can be calculated GPS radius is roughly 35 metres. The time the bus spends for a single stop, or all stops of a line. For a stop vi, we can for example calculate the average (departure) within the radius of stop vi is known as dwell time of stop punctuality Q¯i on a trip p as follows: vi (DTi). Within this GPS radius the bus stops to let pas- sengers board or alight the bus. Doors open within a stop's GPS radius. The time that the bus' doors are open within ki the radius of stop vi is defined as door open time (DOTi). P act sched Di;j − Di;j Bus operators have a specific itinerary of trips that they j=1 Q¯i = (2) drive during the day, this is called the operators' run R ⊂ P . ki A run implies that operators possibly have to switch buses where: at terminals. Buses also have a specific itinerary of trips C ⊂ P which called the bus' circulation. A bus circulation ki: number of buses departing from stop i sched could be on the same line, but a bus may also switch lines, Di;j : scheduled departure time at stop i of vehicle j thus changing routes. act Buses can also enter or leave the system at terminals. Di;j : actual departure time at stop i of vehicle j Some parts of the day (off-peak hours) may have longer headways, which is the time between one bus and the next bus on the same trip. This means total bus capacity is re- The formulation in Equation 2 has the downside that duced and some buses return to the garage to be stored. it does not indicate if vehicles depart too early or too The drive from and to the garage is not indicated as a trip, late, but compensates departures that are too early but is called deadhead. This happens at the start and end with departures that are too late. One solution is to of a bus' circulation. A bus can have multiple circulations take the absolute value of the difference, but then trips during the day thus also having multiple deadheads.
Load more

Recommended publications
  • Analysis and Simulation of Intervention Strategies Against Bus Bunching by Means of an Empirical Agent‑Based Model
    This document is downloaded from DR‑NTU (https://dr.ntu.edu.sg) Nanyang Technological University, Singapore. Analysis and simulation of intervention strategies against bus bunching by means of an empirical agent‑based model Quek, Wei Liang; Chung, Ning Ning; Saw, Vee‑Liem; Chew, Lock Yue 2021 Quek, W. L., Chung, N. N., Saw, V. & Chew, L. Y. (2021). Analysis and simulation of intervention strategies against bus bunching by means of an empirical agent‑based model. Complexity, 2021. https://dx.doi.org/10.1155/2021/2606191 https://hdl.handle.net/10356/146829 https://doi.org/10.1155/2021/2606191 © 2021 Wei Liang Quek et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Downloaded on 30 Sep 2021 12:08:52 SGT Hindawi Complexity Volume 2021, Article ID 2606191, 24 pages https://doi.org/10.1155/2021/2606191 Research Article Analysis and Simulation of Intervention Strategies against Bus Bunching by means of an Empirical Agent-Based Model Wei Liang Quek,1 Ning Ning Chung,2 Vee-Liem Saw ,3,4 and Lock Yue Chew 3,4,5 1School of Humanities, Nanyang Technological University, 639818, Singapore 2Centre for University Core, Singapore University of Social Sciences, 599494, Singapore 3Division of Physics and Applied Physics, School of Physical and Mathematical Sciences, Nanyang Technological University, 637371, Singapore 4Data Science & Artificial Intelligence Research Centre, Nanyang Technological University, 639798, Singapore 5Complexity Institute, Nanyang Technological University, 637723, Singapore Correspondence should be addressed to Lock Yue Chew; [email protected] Received 27 April 2020; Revised 8 August 2020; Accepted 3 September 2020; Published 8 January 2021 Academic Editor: Tingqiang Chen Copyright © 2021 Wei Liang Quek et al.
    [Show full text]
  • Bus Bunching Modelling and Control: a Passenger-Oriented Approach
    CASPT 2018 Extended Abstract Bus Bunching Modelling and Control: A Passenger-oriented Approach Dong Zhao Abstract Introduction Bus reliability is one of the crucial element that describe the performance of the bus system operation. Due to the unreliable transit environment as well as the flexible internal operation, bus irregularity increasingly becomes an issue, especially in big cities with a massive demand. The uncertain bus operation lead to an imbalance of demand and supplement which influences the efficiency and effectivity of this transit. This kind of unreliability enables our bus becomes less attractive comparing with other public transportation such as metro and train. Those well-timetable-based mode have the operational advantage of being separable from the other traffic and have a less likelihood of being interrupted by external influence factors such as traffic lights or road constructions, which seems to be more reliable for the passenger. Also, due to the reliable operation, the real-time information provided for passenger is more trustable and the passenger arriving pattern are more similar to the uniform pattern, which is proved can increase the level of service reliability. On the other hand, the part of the travel demand that should be satisfied by bus obliged to be reallocated to other transit mode. The decreases of the efficiency and comfortability because of this extra demand would even compel those affordable people to travel by private vehicles which may increase the road pressure. Therefore, it is essential to improve the reliability of the bus service. One of the measurement of the bus unreliability is the level and extent of bus bunching.
    [Show full text]
  • Headway Adherence. Detection and Reduction of the Bus Bunching Effect
    HEADWAY ADHERENCE. DETECTION AND REDUCTION OF THE BUS BUNCHING EFFECT Josep Mension Camps Director Central Services and Deputy Chief Officer of Bus Network. Transports Metropolitans de Barcelona (TMB). Miquel Estrada Romeu Associate Professor. Universitat Politècnica de Catalunya- BarcelonaTECH. 1. INTRODUCTION Transit systems should provide a good performance to compete against the wide usage of cars in metropolitan areas. The level of service of these systems relies on a proper temporal and spatial coverage provision (high frequencies, low stop spacings) as well as significant regularity and comfort. In this way, bus systems in densely populated cities usually operate at short headways (10 minutes or less). However, in these busy routes, any delay suffered by a single bus is propagated to the whole bus fleet. This fact causes vehicle bunching and unstable time-headways. In real bus lines, we usually see that two or more vehicles arrive together or in close succession, followed by a long gap between them. There are many sources of potential external disruptions in the service of one bus: illegal parking in the bus lane, failure in the doors opening system, traffic jams, etc. However, some intrinsic characteristics of transit systems and traffic management may also induce delays at specific vehicles such as traffic signal coordination and irregular passenger arrivals at stops. These facts make the bus motion unstable. Therefore, bus bunching is a common problem in the real operation of buses all over the world that must be addressed. The crucial issue is that bus bunching has a great impact on both users and agency cost. From a passenger perspective, the bus bunching phenomena increases the travel time of passengers (riding and waiting time) and worsens the vehicle occupancy.
    [Show full text]
  • Multiline Bus Bunching Control Via Vehicle Substitution
    Transportation Research Part B 126 (2019) 68–86 Contents lists available at ScienceDirect Transportation Research Part B journal homepage: www.elsevier.com/locate/trb Multiline Bus Bunching Control via Vehicle Substitution ∗ Antoine Petit, Chao Lei, Yanfeng Ouyang Department of Civil and Environmental Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA a r t i c l e i n f o a b s t r a c t Article history: Traditional bus bunching control methods (e.g., adding slack to schedules, adapting cruis- Received 2 August 2018 ing speed), in one way or another, trade commercial speed for better system stability and, Revised 13 April 2019 as a result, may impose the burden of additional travel time on passengers. Recently, a dy- Accepted 20 May 2019 namic bus substitution strategy, where standby buses are dispatched to take over service Available online 6 June 2019 from late/early buses, was proposed as an attempt to enhance system reliability without Keywords: sacrificing too much passenger experience. This paper further studies this substitution Bus bunching strategy in the context of multiple bus lines under either time-independent or time- Transit reliability varying settings. In the latter scenario, the fleet of standby buses can be dynamically Approximate dynamic programming utilized to save on opportunity costs. We model the agency’s substitution decisions and Multiline control retired bus repositioning decisions as a stochastic dynamic program so as to obtain the optimal policy that minimizes the system-wide costs. Numerical results show that the dynamic substitution strategy can benefit from the “economies of scale” by pooling the standby fleet across lines, and there are also benefits from dynamic fleet management when transit demand varies over time.
    [Show full text]
  • An Approach to Reducing Bus Bunching
    UC Berkeley Dissertations Title An Approach to Reducing Bus Bunching Permalink https://escholarship.org/uc/item/6zc5j8xg Author Pilachowski, Joshua Michael Publication Date 2009-12-01 eScholarship.org Powered by the California Digital Library University of California University of California Transportation Center UCTC Dissertation No. 165 An Approach to Reducing Bus Bunching Joshua Michael Pilachowski University of California, Berkeley 2009 An Approach to Reducing Bus Bunching by Joshua Michael Pilachowski A dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Engineering—Civil and Environmental Engineering in the Graduate Division of the University of California, Berkeley Committee in charge: Professor Carlos F. Daganzo Professor Samer M. Madanat Professor Laurent El Ghaoui Fall 2009 An Approach to Reducing Bus Bunching Copyright 2009 by Joshua Michael Pilachowski i Abstract An Approach to Reducing Bus Bunching by Joshua Michael Pilachowski Doctor of Philosophy in Engineering University of California, Berkeley Professor Carlos F. Daganzo, Chair The tendency of buses to bunch is a problem that was defined almost 50 years ago. Since then, there has been a significant amount of work done on the problem; however, the tendency of the current literature is either to only focus on the surface causes or to rely on simulation to create results instead of model formulation. With GPS installed on many buses throughout the world, the data is only being used for monitoring and informing the user. This research proposes a new approach to solving the problem that uses the GPS data to directly counteract the cause of the bunching by allowing the buses to cooperate with each other and determine their speed based on relative position.
    [Show full text]
  • Empirical Analysis of Bus Bunching Characteristics Based on Bus AVL/APC Data
    Portland State University PDXScholar Civil and Environmental Engineering Faculty Publications and Presentations Civil and Environmental Engineering 1-2015 Empirical Analysis of Bus Bunching Characteristics Based on Bus AVL/APC Data Wei Feng Portland State University Miguel A. Figliozzi Portland State University, [email protected] Follow this and additional works at: https://pdxscholar.library.pdx.edu/cengin_fac Part of the Civil Engineering Commons, Environmental Engineering Commons, and the Transportation Engineering Commons Let us know how access to this document benefits ou.y Citation Details Feng, Wei and Figliozzi, Miguel A., "Empirical Analysis of Bus Bunching Characteristics Based on Bus AVL/ APC Data" (2015). Civil and Environmental Engineering Faculty Publications and Presentations. 315. https://pdxscholar.library.pdx.edu/cengin_fac/315 This Post-Print is brought to you for free and open access. It has been accepted for inclusion in Civil and Environmental Engineering Faculty Publications and Presentations by an authorized administrator of PDXScholar. Please contact us if we can make this document more accessible: [email protected]. 1 Empirical Analysis of Bus Bunching Characteristics Based on Bus AVL/APC Data 2 3 4 5 6 Wei Feng* 7 PhD. Researcher 8 Portland State University 9 [email protected] 10 11 12 13 14 Miguel Figliozzi 15 Associate Professor 16 Portland State University 17 [email protected] 18 19 20 21 22 Mailing Address: 23 Portland State University 24 Civil and Environmental Engineering 25 PO Box 751 26 Portland, OR 97207 27 28 29 30 31 *corresponding author 32 33 34 35 36 Word count: 4,292 words + (11 Figures + 1 Table) * 250 = 7,292 words 37 38 39 40 Submitted to the 94th Annual Meeting of Transportation Research Board, 41 January 11-15, 2015 42 43 Feng and Figliozzi 1 1 Abstract 2 3 Bus bunching takes place when headways between buses are irregular.
    [Show full text]
  • Definition and Properties of Alternative Bus Service Reliability Measures at the Stop Level
    Definition and Properties of Alternative Bus Service Reliability Measures at the Stop Level Definition and Properties of Alternative Bus Service Reliability Measures at the Stop Level Meead Saberi and Ali Zockaie K., Northwestern University Wei Feng, Portland State University Ahmed El-Geneidy, McGill University Abstract TheTransit Capacity and Quality of Service Manual (TCQSM) provides transit agen- cies with tools for measuring system performance at different levels of operation. Bus service reliability, one of the key performance measures, has become a major con- cern of both transit operators and users because it significantly affects user experi- ence and service quality perceptions. The objective of this paper is to assess the exist- ing reliability measures proposed by TCQSM and develop new ones at the bus stop level. The latter are not suggested as replacements for the existing measures; rather, they are complementary. Using empirical data from archived Bus Dispatch System (BDS) data in Portland, Oregon, a number of key characteristics of distributions of delay (schedule deviation) and headway deviation are identified. In addition, the proposed reliability measures at the stop level are capable of differentiating between the costs of being early versus late. The results of this study can be implemented in transit operations for use in improving schedules and operations strategies. Also, transit agencies can use the proposed reliability measures to evaluate and prioritize stops for operational improvement purposes. 97 Journal of Public Transportation, Vol. 16, No. 1, 2013 Introduction Monitoring of the performance measures of public transportation systems has improved since advanced surveillance, monitoring, and management systems have been deployed by transit agencies worldwide.
    [Show full text]
  • Bus Bunching As a Synchronisation Phenomenon Vee-Liem Saw 1,2, Ning Ning Chung3, Wei Liang Quek1, Yi En Ian Pang1 & Lock Yue Chew1,2,3
    www.nature.com/scientificreports OPEN Bus bunching as a synchronisation phenomenon Vee-Liem Saw 1,2, Ning Ning Chung3, Wei Liang Quek1, Yi En Ian Pang1 & Lock Yue Chew1,2,3 Bus bunching is a perennial phenomenon that not only diminishes the efciency of a bus system, but Received: 5 March 2019 also prevents transit authorities from keeping buses on schedule. We present a physical theory of buses Accepted: 18 April 2019 serving a loop of bus stops as a ring of coupled self-oscillators, analogous to the Kuramoto model. Published: xx xx xxxx Sustained bunching is a repercussion of the process of phase synchronisation whereby the phases of the oscillators are locked to each other. This emerges when demand exceeds a critical threshold. Buses also bunch at low demand, albeit temporarily, due to frequency detuning arising from diferent human drivers’ distinct natural speeds. We calculate the critical transition when complete phase locking (full synchronisation) occurs for the bus system, and posit the critical transition to completely no phase locking (zero synchronisation). The intermediate regime is the phase where clusters of partially phase locked buses exist. Intriguingly, these theoretical results are in close correspondence to real buses in a university’s shuttle bus system. A self-oscillator is a unit with an internal source of energy (to overcome dissipation) that continuously and auton- omously performs rhythmic motion. It is stable against perturbations on its amplitude but neutrally stable over perturbations on its phase. Te latter allows an array of coupled self-oscillators to undergo phase synchronisa- tion, as individual members afect others’ phases through their nonlinear interactions1.
    [Show full text]
  • Characteristics of Bus Rapid Transit for Decision-Making
    Project No: FTA-VA-26-7222-2004.1 Federal United States Transit Department of August 2004 Administration Transportation CharacteristicsCharacteristics ofof BusBus RapidRapid TransitTransit forfor Decision-MakingDecision-Making Office of Research, Demonstration and Innovation NOTICE This document is disseminated under the sponsorship of the United States Department of Transportation in the interest of information exchange. The United States Government assumes no liability for its contents or use thereof. The United States Government does not endorse products or manufacturers. Trade or manufacturers’ names appear herein solely because they are considered essential to the objective of this report. Form Approved REPORT DOCUMENTATION PAGE OMB No. 0704-0188 Public reporting burden for this collection of information is estimated to average 1 hour per response, including the time for reviewing instructions, searching existing data sources, gathering and maintaining the data needed, and completing and reviewing the collection of information. Send comments regarding this burden estimate or any other aspect of this collection of information, including suggestions for reducing this burden, to Washington Headquarters Services, Directorate for Information Operations and Reports, 1215 Jefferson Davis Highway, Suite 1204, Arlington, VA 22202-4302, and to the Office of Management and Budget, Paperwork Reduction Project (0704-0188), Washington, DC 20503. 1. AGENCY USE ONLY (Leave blank) 2. REPORT DATE 3. REPORT TYPE AND DATES August 2004 COVERED BRT Demonstration Initiative Reference Document 4. TITLE AND SUBTITLE 5. FUNDING NUMBERS Characteristics of Bus Rapid Transit for Decision-Making 6. AUTHOR(S) Roderick B. Diaz (editor), Mark Chang, Georges Darido, Mark Chang, Eugene Kim, Donald Schneck, Booz Allen Hamilton Matthew Hardy, James Bunch, Mitretek Systems Michael Baltes, Dennis Hinebaugh, National Bus Rapid Transit Institute Lawrence Wnuk, Fred Silver, Weststart - CALSTART Sam Zimmerman, DMJM + Harris 8.
    [Show full text]
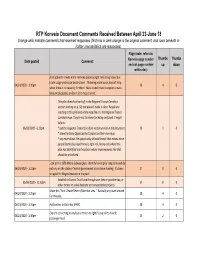
  • RTP Konveio Document Comments Received Between April 23-June 18
    RTP Konveio Document Comments Received Between April 23-June 18 Orange cells indicate comments that received responses (first row in dark orange is the original comment, and rows beneath in lighter orange/italics are responses) Page (note: refers to Thumbs Thumbs Date posted Comment Konveio page number and not page number up down within doc) Add option to create more rail lines (subway/light rail) along heavy bus route usage and major destinations. Throwing more buses doesn't help 04/24/2020 - 1:20pm 26 4 0 when there is no capacity for them. Mass transit must transport a mass amount of people, or else it isn't mass transit. This plan does that (sort of) in the Regional Transit Corridors section starting on p. 58, but doesn't make it clear. People are reacting to this pink and white map like it is the Regional Transit Corridors map. They're not to blame for being confused. It might help to: 06/03/2020 - 6:12pm * put the Regional Transit Corridors section earlier in the document 26 1 0 * show the Early Opportunity Corridors on their own map * say more about the opportunity to build transit that moves more people faster (bus rapid transit, light rail, heavy rail) where this plan has identified are the places where improvements like that should be prioritized Look at the 1978 Metro Subway plan. Identify funding for long term and do 04/24/2020 - 1:22pm not rely on the state or federal government to continue funding. It's been 27 8 0 stripped for illogical reasons in the past! Establish a Transit Trust Fund through user fees or gasoline tax, or 05/06/2020 - 11:50pm 27 8 0 other means to solely dedicate to transportation projects.
    [Show full text]
  • Speeding up Chicago's Buses
    BACK ON THE BUS: SPEEDING UP CHICAGO’S BUSES Funded by TABLE OF CONTENTS EXECUTIVE SUMMARY 1 WHAT RIDERS ARE SAYING ABOUT CHICAGO’S BUS SERVICE 5 SERVICE UPGRADES 6 Priority improvements to make Chicago’s buses faster and more reliable Dedicated bus lanes 6 Traffic signal improvements 8 Faster boarding 9 Route profiles & recommendations 11 POLICY CHANGES 16 What’s next? 19 ACKNOWLEDGMENTS 20 EXECUTIVE SUMMARY As Chicago strives to become a more connected, spoke rail system continues to be a good option prosperous, and equitable city, elected officials for people who live and work along the CTA train and transit agency leaders must take action to lines and in the Loop, but many neighborhoods improve bus service. More than half of CTA trips lack access to it. Without more investment in bus in Chicago are made by bus and it’s one of the service, Chicago risks more people abandoning most affordable transportation options in many transit for transportation options that are more neighborhoods where people can’t easily access expensive and less efficient, healthy, and green. the El train. Every day, buses are connecting In an era of limited funding at all levels of people to jobs, schools, and other critical services government, bus upgrades are cheaper and can while taking up far less space on the road than be implemented faster than rail modernization private vehicles. While buses continue to play a and expansion. The next several years present central role in the city’s transportation system, an opportunity to make timely, cost-effective there are signs that quality bus service is under improvements to bus service while continuing threat in a changing transportation environment.
    [Show full text]
  • Bus Bunching Modelling and Control: a Passenger-Oriented Approach
    Bus Bunching Modelling and Control: A Passenger-oriented Approach Dong Zhao School of Civil Engineering Faculty of Engineering The University of Sydney A thesis submitted to fulfil requirements for the degree of Master of Philosophy 16 June, 2019 This is to certify that to the best of my knowledge, the content of this thesis is my own work. This thesis has not been submitted for any degree or other purposes. Dong Zhao 16 June, 2019 Abstract Bus bunching indicated the situation when two originally equally spaced bus services running close to each other as the earlier service runs increasingly late or the later service runs ahead. This phenomenon corresponds to bus services unreliability due to the extra passenger boarding, improper dispatching or travelling irregularity resulting in traffic congestions, for example. Bunched buses deteriorate passengers travel experience on public transport services that share the infrastructure with other travel modes. This has become a growing concern in big cities where traffic problems are common. It is challenging to improve the bus service reliability as a variety of chaotic sources, such as traffic congestion or unpredictable travel demand, can affect it. In order to understand the main influence factors of bus bunching in Sydney, this thesis first investigates in detail the bus service operations in Sydney and develops three passenger-oriented bus bunching mitigation approaches to improve the bus service reliability. The real picture of bus bunching in Sydney is scrutinised based on the Sydney bus system automatic vehicle location (AVL) field data. By developing the bus bunching distributions based on different criteria, such as stop location, the bus running direction, month, weekday, time and route number, bus bunching is observed to have a higher possibility in occurring during afternoon peak hours on weekdays in March and July.
    [Show full text]