Evaluation of the Effect of Relative Humidity of Air on the Coefficients of Critical Flow Venturi Nozzles
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Investigating Applicability of Evaporative Cooling Systems for Thermal Comfort of Poultry Birds in Pakistan
applied sciences Article Investigating Applicability of Evaporative Cooling Systems for Thermal Comfort of Poultry Birds in Pakistan Hafiz M. U. Raza 1, Hadeed Ashraf 1, Khawar Shahzad 1, Muhammad Sultan 1,* , Takahiko Miyazaki 2,3, Muhammad Usman 4,* , Redmond R. Shamshiri 5 , Yuguang Zhou 6 and Riaz Ahmad 6 1 Department of Agricultural Engineering, Bahauddin Zakariya University, Bosan Road, Multan 60800, Pakistan; [email protected] (H.M.U.R.); [email protected] (H.A.); [email protected] (K.S.) 2 Faculty of Engineering Sciences, Kyushu University, Kasuga-koen 6-1, Kasuga-shi, Fukuoka 816-8580, Japan; [email protected] 3 International Institute for Carbon-Neutral Energy Research (WPI-I2CNER), Kyushu University, 744 Motooka, Nishi-ku, Fukuoka 819-0395, Japan 4 Institute for Water Resources and Water Supply, Hamburg University of Technology, Am Schwarzenberg-Campus 3, 20173 Hamburg, Germany 5 Leibniz Institute for Agricultural Engineering and Bioeconomy, Max-Eyth-Allee 100, 14469 Potsdam-Bornim, Germany; [email protected] 6 Bioenergy and Environment Science & Technology Laboratory, College of Engineering, China Agricultural University, Beijing 100083, China; [email protected] (Y.Z.); [email protected] (R.A.) * Correspondence: [email protected] (M.S.); [email protected] (M.U.); Tel.: +92-333-610-8888 (M.S.); Fax: +92-61-9210298 (M.S.) Received: 4 June 2020; Accepted: 24 June 2020; Published: 28 June 2020 Abstract: In the 21st century, the poultry sector is a vital concern for the developing economies including Pakistan. The summer conditions of the city of Multan (Pakistan) are not comfortable for poultry birds. -
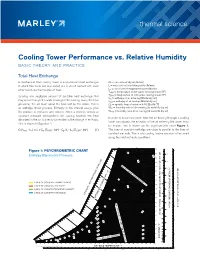
Thermal Science Cooling Tower Performance Vs. Relative Humidity
thermal science Cooling Tower Performance vs. Relative Humidity BASIC THEORY AND PRACTICE Total Heat Exchange A mechanical draft cooling tower is a specialized heat exchanger G = mass rate of dry air [lb/min] in which two fluids (air and water) are in direct contact with each L = mass rate of circulating water [lb/min] other to induce the transfer of heat. Le = mass rate of evaporated water [lb/min] THW = temperature of hot water entering tower [°F] Ignoring any negligible amount of sensible heat exchange that TCW = temperature of cold water leaving tower [°F] hin = enthalpy of air entering [Btu/lb/dry air] may occur through the walls (casing) of the cooling tower, the heat hout = enthalpy of air leaving [Btu/lb/dry air] gained by the air must equal the heat lost by the water. This is Cp = specific heat of water = 4.18 [Btu/lb-°F] an enthalpy driven process. Enthalpy is the internal energy plus Win = humidity ratio of air entering [lb water/lb dry air] the product of pressure and volume. When a process occurs at Wout = humidity ratio of air leaving [lb water/lb dry air] constant pressure (atmospheric for cooling towers), the heat In order to know how much heat the air flowing through a cooling absorbed in the air is directly correlated to the change in enthalpy. tower can absorb, the enthalpy of the air entering the tower must This is shown in Equation 1. be known. This is shown on the psychrometric chart Figure 1. G (hout - hin) = L x Cp (THW - 32°) - Cp (L - Le)(TCW - 32°) (1) The lines of constant enthalpy are close to parallel to the lines of constant wet bulb. -

Recommended Qualification Test Procedure for Solar Absorber.Pdf
Date: 2004-09-10 Editor Bo Carlsson1 IEA Solar Heating and Cooling Program Task 27 Performance of Solar Façade Components Project: Service life prediction tools for Solar Collectors Recommended qualification test procedure for solar absorber surface durability 1 Address: SP Swedish National Testing and Research Institute, P.O.Box 857, SE-50115 Borås, e-mail: [email protected] Contents Page Foreword.............................................................................................................................................................iv Introduktion .........................................................................................................................................................v 1 Scope ......................................................................................................................................................1 2 Normative references ............................................................................................................................1 3 Terms and definitions ...........................................................................................................................2 4 Requirements and classification..........................................................................................................3 5 Test methods for assessing material properties as measure of absorber performance...............4 5.1 Sampling and preparation of test specimens.....................................................................................4 -

Psychrometrics Outline
Psychrometrics Outline • What is psychrometrics? • Psychrometrics in daily life and food industry • Psychrometric chart – Dry bulb temperature, wet bulb temperature, absolute humidity, relative humidity, specific volume, enthalpy – Dew point temperature • Mixing two streams of air • Heating of air and using it to dry a product 2 Psychrometrics • Psychrometrics is the study of properties of mixtures of air and water vapor • Water vapor – Superheated steam (unsaturated steam) at low pressure – Superheated steam tables are on page 817 of textbook – Properties of dry air are on page 818 of textbook – Psychrometric charts are on page 819 & 820 of textbook • What are these properties of interest and why do we need to know these properties? 3 Psychrometrics in Daily Life • Sea breeze and land breeze – When and why do we get them? • How do thunderstorms, hurricanes, and tornadoes form? • What are dew, fog, mist, and frost and when do they form? • When and why does the windshield of a car fog up? – How do you de-fog it? Is it better to blow hot air or cold air? Why? • Why do you feel dry in a heated room? – Is the moisture content of hot air lower than that of cold air? • How does a fan provide relief from sweating? • How does an air conditioner provide relief from sweating? • When does a soda can “sweat”? • When and why do we “see” our breath? • Do sailboats perform better at high or low relative humidity? Key factors: Temperature, Pressure, and Moisture Content of Air 4 Do Sailboats Perform Better at low or High RH? • Does dry air or moist air provide more thrust against the sail? • Which is denser – humid air or dry air? – Avogadro’s law: At the same temperature and pressure, the no. -

Model 1830, 1850 & 1850W Dehumidifier Owner's Manual
Model 1830, 1850 & 1850W Dehumidifier Owner’s Manual PLEASE LEAVE THIS MANUAL WITH THE HOMEOWNER Installed by: _________________________________ Installer Phone: _______________________ Date Installed: _______________ ON/OFF button Up/Down Dehumidifer Control Outlet used to turn buttons used to dehumidifier on change humidity and off setting MODE button used for optional ventilation feature Inlet Filter Access Drain Power Door Switch 90-1874 WHOLE HOME Dehumidification The Aprilaire® Dehumidifier controls the humidity level in your entire home. A powerful blower inside the dehumidifier draws air into the cabinet, filters the air and removes moisture, then discharges the dry air into the HVAC system or dedicated area of the home. Inside the cabinet, a sealed refrigeration system removes moisture by moving the air through a series of tubes and fins that are kept colder than the dew point of the incoming air. The dew point is the temperature at which moisture in the air will condense, much like what occurs on the outside of a cold glass on a hot summer day. The condensed moisture drips into the dehumidifier drain pan to a drain tube routed to the nearest floor drain or condensate pump. After the moisture is removed, the air moves through a second coil where it is reheated before being sent back into the home. The air leaving the dehumidifier will be warmer and drier than the air entering the dehumidifier. SETTING THE DESIRED HUMIDITY LEVEL The dehumidifier on-board control will display the humidity setting when not running, and ENERGY SavinGS TIPS displays the measured humidity when running. Energy Savings Tip #1: Adjust the humidity setting to be as high as is comfortable to reduce dehumidifier run time. -

Factors Affecting Indoor Air Quality
Factors Affecting Indoor Air Quality The indoor environment in any building the categories that follow. The examples is a result of the interaction between the given for each category are not intended to site, climate, building system (original be a complete list. 2 design and later modifications in the Sources Outside Building structure and mechanical systems), con- struction techniques, contaminant sources Contaminated outdoor air (building materials and furnishings, n pollen, dust, fungal spores moisture, processes and activities within the n industrial pollutants building, and outdoor sources), and n general vehicle exhaust building occupants. Emissions from nearby sources The following four elements are involved n exhaust from vehicles on nearby roads Four elements— in the development of indoor air quality or in parking lots, or garages sources, the HVAC n loading docks problems: system, pollutant n odors from dumpsters Source: there is a source of contamination pathways, and or discomfort indoors, outdoors, or within n re-entrained (drawn back into the occupants—are the mechanical systems of the building. building) exhaust from the building itself or from neighboring buildings involved in the HVAC: the HVAC system is not able to n unsanitary debris near the outdoor air development of IAQ control existing air contaminants and ensure intake thermal comfort (temperature and humidity problems. conditions that are comfortable for most Soil gas occupants). n radon n leakage from underground fuel tanks Pathways: one or more pollutant pathways n contaminants from previous uses of the connect the pollutant source to the occu- site (e.g., landfills) pants and a driving force exists to move n pesticides pollutants along the pathway(s). -

Indoor Air Quality in Commercial and Institutional Buildings
Indoor Air Quality in Commercial and Institutional Buildings OSHA 3430-04 2011 Occupational Safety and Health Act of 1970 “To assure safe and healthful working conditions for working men and women; by authorizing enforcement of the standards developed under the Act; by assisting and encouraging the States in their efforts to assure safe and healthful working conditions; by providing for research, information, education, and training in the field of occupational safety and health.” This publication provides a general overview of a particular standards-related topic. This publication does not alter or determine compliance responsibili- ties which are set forth in OSHA standards, and the Occupational Safety and Health Act of 1970. More- over, because interpretations and enforcement poli- cy may change over time, for additional guidance on OSHA compliance requirements, the reader should consult current administrative interpretations and decisions by the Occupational Safety and Health Review Commission and the courts. Material contained in this publication is in the public domain and may be reproduced, fully or partially, without permission. Source credit is requested but not required. This information will be made available to sensory- impaired individuals upon request. Voice phone: (202) 693-1999; teletypewriter (TTY) number: 1-877- 889-5627. Indoor Air Quality in Commercial and Institutional Buildings Occupational Safety and Health Administration U.S. Department of Labor OSHA 3430-04 2011 The guidance is advisory in nature and informational in content. It is not a standard or regulation, and it neither creates new legal obligations nor alters existing obligations created by OSHA standards or the Occupational Safety and Health Act. -

Modern Evaporative Coolers Not All Evaporative Coolers Are Created Equal
Modern Evaporative Coolers Not all evaporative coolers are created equal. Modern machines operate more efficiently and with much less fuss than the old swamp coolers did. ADOBE ADOBE Here is an inside view (left) and an outside view (right) of a modern evaporative cooler by Adobe. by Larry Kinney dampers, also known as up ducts, in the fer the better comfort and fresh, clean ceilings of rooms on the top story. The air our systems give them. The $300 we ave Emmitt owns Direct Drive process is controlled by a multifunction save them on their utility bill each sum- Service, a company in Colorado thermostat that has the smarts to throttle mer just pays for a barbeque with 50 of Dthat specializes in efficient low- back the fan speed when the setpoint their closest friends.” mass boilers—and high-efficiency evap- temperature is about to be met, rinses Emmitt’s retrofit business is also doing orative coolers. We’re not talking swamp out the reservoir to keep water and air quite well. Colorado homeowners who coolers on the roof of a mobile home; clean, and partially automates much of have never had cooling systems generally Emmitt’s staff install coolers in the attics the end-of-season maintenance. tend to install conventional A/C of large, site-built homes. The coolers “We install modern evaporative systems—as do those who are pull in air from large gable vents, cool it cooler systems in new homes that cost disenchanted with their old swamp cool- by 30°F or so, and distribute it via several $2 million,”reports Emmitt. -

Humidity and Occupants Presentation
Humidity and Occupants What the Latest in Humidity Research Means for You Presenters Matt Nowak North American Sales Manager Armstrong International Eric Brodsky, PE Director of Technology Research Products Inc. / Aprilaire / DriSteem Duncan Curd General Manager Nortec Humidity Ltd. Jeremy Wolfe National Sales & Marketing Manager CAREL USA Agenda 1. Fundamentals of Humidity • Key Terms and Definitions • How indoor humidity changes throughout the year • Where humidification matter most 2. Humidity and People • Historical Research • Impacts of moisture to the human body • Recent advances in humidity research 3. Recent Research • Microbiome Study Details • Example of Hospital Savings • Results and Recommendations 4. Humidity in Your Building • Technologies for Humidification • Cooling and Humidifying with Adiabatic Systems • Humidification with Steam • Case Studies / Installation Examples What is Humidity and How Do We Measure It? Humidity • The amount of water vapor in the air • Measured in “Absolute” or “Relative” terms Absolute Humidity • Mass of water in particular volume of air • Expressed as mass (grains/lbda or gw/kgda) Relative Humidity • Amount of water vapor in the air relative to how much it can hold at a given temperature (%) 25 20 15 Maximum Moisture Content Of Air Depends 10 5 0 On Air Temperature Grains Grains of/ Water Cubic Foot of Air 0 5 -5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 -10 100 Air Temperature (F) How Much Water Can the Air Hold? Air Heated From 10°F @ 100% RH to 70 °F 1 lb (kg) of Air Would Only Be Less Than 10% RH 35°F (2°C) 30 gr (2g/kg) The Psychrometric Chart Typical RH in Las Vegas, NV Typical Temps in Las Vegas, NV Need for Humidification Summer (July 19th) – 104F @ 10% RH = 72F @ 27.5% RH Winter (Dec. -

The Heat Index "Equation" (Or, More Than You Ever Wanted to Know About Heat Index)
SR 90-23 Technical Attachment 7/1/90 The Heat Index "Equation" (or, More Than You Ever Wanted to Know About Heat Index) Lans P. Rothfusz Scientific Services Division NWS Southern Region Headquarters, Fort Worth, TX Now that summer has spread its oppressive ridge over most of the Southern Region, NWS phones are ringing off their hooks with questions about the Heat Index. Many questions regard the actual equation used in calculating the Heat Index. Some callers are satisfied with the response that it is extremely complicated. Some are satisfied with the nomogram (see Attachment 1). But there are a few who will settle for nothing less than the equation itself. No true equation for the Heat Index exists. Heat Index values are derived from a collection of equations that comprise a model. This Technical Attachment presents an equation that approximates the Heat Index and, thus, should satisfy the latter group of callers. The Heat Index (or apparent temperature) is the result of extensive biometeorological studies. The parameters involved in its calculation are shown below (from Steadman, 1979). Each of these parameters can be described by an equation but they are given assumed magnitudes (in parentheses) in order to simplify the model. # Vapor pressure. Ambient vapor pressure of the atmosphere. (1.6 kPa) # Dimensions of a human. Determines the skin's surface area. (5' 7" tall, 147 pounds) # Effective radiation area of skin. A ratio that depends upon skin surface area. (0.80) # Significant diameter of a human. Based on the body's volume and density. (15.3 cm) # Clothing cover. -

Proper Moisture Measurement… Its the Dew Point Stupid
Page 1 of 6 Measuring The Right Thing For Humidity Control… It’s the Dew Point Stupid! By Mike Schell, AirTest Technologies Corp. portion of sensible and latent removal that is A version of this article appeared in the June 2004 provided by a particular system. Most systems edition of Indoor Air Connections and in the August today operate with a sensible heat ratio of 0.8 to edition of the Automated Buildings Webzine. Mike 0.95 meaning that the larger portion of energy can be reached at [email protected] or at 805 consumption of the system is devoted to sensible 687-3175 cooling (80 –95%) while the remaining 0.05 to 0.5 of the ratio (5-20%) is dedicated to latent heat Introduction removal or humidity control. The old quality mantra “if you can’t measure it, you The S/LR report points out that buildings, to be can’t control it” is one of those universal truisms that properly cooled and dehumidified have their own can easily be applied to moisture control and sensible heat ratio requirement. The report shows dehumidification in buildings. The proliferation of how over the past 30 years how a perfect match mold and moisture related problems in buildings between the SHR of cooling equipment and SHR today is significantly due to the fact that we do not requirements of buildings has drastically changed. have the proper measurement feedback in buildings This divergence of equipment vs building SHR to properly control moisture. This should not be a forms the foundation for many of the moisture surprise. -

Three Methods to Evaluate the Use of Evaporative Cooling for Human Thermal Comfort
Tecnologia/Technology THREE METHODS TO EVALUATE THE USE OF EVAPORATIVE COOLING FOR HUMAN THERMAL COMFORT J. R. Camargoa, ABSTRACT b C. D. Ebinuma , This paper presents three methods that can be used as reference for efficient and S. Cardosoa use of evaporative cooling systems, applying it, latter, to several Brazilian cities, characterized by different climates. Initially it presents the basic aUniversidade de Taubaté principles of direct and indirect evaporative cooling and defines the Departamento de Engenharia Mecânica effectiveness of the systems. Afterwards, it presents three methods that allows to determinate where the systems are more efficient. It concludes Rua Daniel Danelli, s/n that evaporative cooling systems have a very large potential to propitiate CEP. 12060-440, Taubaté, SP, Brasil thermal comfort and can still be used as an alternative to conventional bUniversidade do Estado de São Paulo systems in regions where the design wet bulb temperature is under 24ºC. Departamento de Energia Rua Ariberto Pereira da Cunha, 333 Keywords: Evaporative Cooling, Thermal Comfort, Air Conditioning CEP. 12500-000, Guaratinguetá, SP, Brasil [email protected] INTRODUCTION determinate where, when, how and what is the operational efficiency of these systems and, for this, Air conditioning is responsible for the increase three methods are presented in order to establish of the efficiency of the man in his job as well as for references, applied to several Brazilian cities, his comfort, mainly in warm periods along the year. characterized by different climates. Currently, the most used system is the mechanical The first method is based on Watt (1963) and vapor compression system.