Quantifying Phases in Homogeneous Twisted Birefringent Medium
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Vidyasagar College of Optometry and Vision Science
BACHELOR IN OPTOMETRY (B.OPTOM) PROGRAMME • FOUR YEAR DEGREE PROGRAMME College Vidyasagar and Vision Science and Vision of Optometry VCOVS WWW.VCOVS.ORG [email protected] About Optometry Optometry is a healthcare profes- registered), and optometrists are sion concerned with the health of the the primary healthcare practition- eyes and related structures, as well ers of the eye and visual system who as vision, visual systems, and vision provide comprehensive eye and information processing in humans. vision care, which includes refrac- tion and dispensing, detection/di- The World Council of Optometry agnosis and management of disease defines Optometry as ahealth - in the eye, and the rehabilitation care profession that is autonomous, of conditions of the visual system. educated, and regulated (licensed or Optometrists An optometrist is an independent CAREER AND SCOPE primary health care provider who ex- All optometrists provide general amines, diagnoses, treats and manages eye and vision care. diseases and disorders of the visual Some optometrists work in a system, the eye and associated struc- general practice, and other optom- tures. etrists work in a more specialized Among the services optometrists render practice such as: are: prescribing glasses and contact lenses, rehabilitation of the visually Contact lenses impaired, and the diagnosis and treat- Geriatrics people in the ment of ocular diseases. Low vision services (for visually 285 world are blind or impaired patients) visually impaired million Occupational vision (to protect -
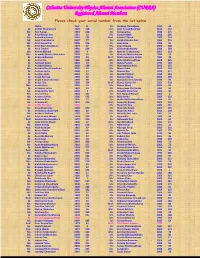
Calcutta University Physics Alumni Association (CUPAA) Registered Alumni Members Please Check Your Serial Number from the List Below Name Year Sl
Calcutta University Physics Alumni Association (CUPAA) Registered Alumni Members Please check your serial number from the list below Name Year Sl. Dr. Joydeep Chowdhury 1993 45 Dr. Abhijit Chakraborty 1990 128 Mr. Jyoti Prasad Banerjee 2010 152 Mr. Abir Sarkar 2010 150 Dr. Kalpana Das 1988 215 Dr. Amal Kumar Das 1991 15 Mr. Kartick Malik 2008 205 Ms. Ambalika Biswas 2010 176 Prof. Kartik C Ghosh 1987 109 Mr. Amit Chakraborty 2007 77 Dr. Kartik Chandra Das 1960 210 Mr. Amit Kumar Pal 2006 136 Dr. Keya Bose 1986 25 Mr. Amit Roy Chowdhury 1979 47 Ms. Keya Chanda 2006 148 Dr. Amit Tribedi 2002 228 Mr. Krishnendu Nandy 2009 209 Ms. Amrita Mandal 2005 4 Mr. Mainak Chakraborty 2007 153 Mrs. Anamika Manna Majumder 2004 95 Dr. Maitree Bhattacharyya 1983 16 Dr. Anasuya Barman 2000 84 Prof. Maitreyee Saha Sarkar 1982 48 Dr. Anima Sen 1968 212 Ms. Mala Mukhopadhyay 2008 225 Dr. Animesh Kuley 2003 29 Dr. Malay Purkait 1992 144 Dr. Anindya Biswas 2002 188 Mr. Manabendra Kuiri 2010 155 Ms. Anindya Roy Chowdhury 2003 63 Mr. Manas Saha 2010 160 Dr. Anirban Guha 2000 57 Dr. Manasi Das 1974 117 Dr. Anirban Saha 2003 51 Dr. Manik Pradhan 1998 129 Dr. Anjan Barman 1990 66 Ms. Manjari Gupta 2006 189 Dr. Anjan Kumar Chandra 1999 98 Dr. Manjusha Sinha (Bera) 1970 89 Dr. Ankan Das 2000 224 Prof. Manoj Kumar Pal 1951 218 Mrs. Ankita Bose 2003 52 Mr. Manoj Marik 2005 81 Dr. Ansuman Lahiri 1982 39 Dr. Manorama Chatterjee 1982 44 Mr. Anup Kumar Bera 2004 3 Mr. -

The Era of Science Enthusiasts in Bengal (1841-1891): Akshayakumar, Vidyasagar and Rajendralala
Indian Journal of History of Science, 47.3 (2012) 375-425 THE ERA OF SCIENCE ENTHUSIASTS IN BENGAL (1841-1891): AKSHAYAKUMAR, VIDYASAGAR AND RAJENDRALALA ARUN KUMAR BISWAS* (Received 14 March 2012) During the nineteenth century, the Indian sub-continent witnessed two distinct outbursts of scientific enthusiasm in Bengal: one led by Rammohun Roy and his compatriots (1820-1840) and the other piloted by Mahendralal Sircar and Eugene Lafont (1860-1910). The intermediate decades were pioneered by the triumvirate: Akshayakumar, Vidyasagar, Rajendralala and a few others. Several scientific journals such as Tattvabodhinī Patrika–, Vivida–rtha Samgraha, Rahasya Sandarbha etc dominated the intellectual environment in the country. Some outstanding scientific books were written in Bengali by the triumvirate.Vidyasagar reformed the science content in the educational curricula. Akshayakumar was a champion in the newly emerging philosophy of science in India. Rajendralala was a colossus in the Asiatic Society, master in geography, archaeology, antiquity studies, various technical sciences, and proposed a scheme for rendering European scientific terms into vernaculars of India. There was a separate Muslim community’s approach to science in the 19th Century India. Key words: Akshayakumar, Botanical Collection, Geography, Muslim Community approach to Science, Phrenology, Rajendralala, Science enthusiasts (1841-1891), Technical Sciences, Triumvirate, Positivism, Vidyasagar INTRODUCTION It can be proposed that the first science movement in India was chiefly concentrated in the city of Calcutta and spanned the period of approximately quarter of a century (1814-39) coinciding with the entry of *Flat 2A, ‘Kamalini’ 69A, Townshend Road, Kolkata-700026 376 INDIAN JOURNAL OF HISTORY OF SCIENCE Rammohun in the city and James Prinsep’s departure from it. -

Principal's Annual Report for the Year 2016-17 Vidyasagar College For
Principal’s Annual Report for the Year 2016-17 Vidyasagar College for Women I take great pleasure in presenting the Annual Report of Vidyasagar Collge for Women documenting its developments and achievements. The year 2016-17 was marked with many events and successes. This can be attributed to the dedication and team spirit of the members of the management, staff and students. The history of the Vidyasagar College For Women (VCFW) goes back to the year 1872 when Vidyasagar College was found by Pandit Iswar Chandra Vidyasagar in the heart of Calcutta. The college began as a separate women‟s section of the Vidyasagar College from the year 1931. In the year 1960 Vidyasagar College for Women grew out of its infancy when it received its affiliation from the University of Calcutta and was established as an independent college solely for young women. The iconic figure of Iswar Chandra Vidyasagar continues to inspire generations of women. A great asset of this college is Pandit Iswar Chandra's own house which is the designated as the 2nd campus of the college. In 2014, Vidyasagar College for Women acquired a Third Campus at 8A Sibnarayan Das Lane, Kolkata: 700006. The Third Campus houses the Central Library of the College, an air-conditioned staff room, an IQAC Room and ICT-enabled classroom, a modern Computer Lab, an Auditorium and several classrooms. VISION The vision of the College is to foster inclusiveness in access to higher education, irrespective of class or caste and to instil students with positive values and a humanistic spirit of service to the wider community. -

VIDYASAGAR COLLEGE 2011-12 ACCREDITED by NAAC a STAR COLLEGE (DBT, Govt
VIDYASAGAR COLLEGE 2011-12 ACCREDITED BY NAAC A STAR COLLEGE (DBT, Govt. of India) PROSPECTUS 2011 CONTENT Welcome …. 03 Admission Process …. 05 Subject Code and Combination …. 06 General Guidelines for Admission 11 About the College …. 13 Attendance …. 13 Schedule of College Test and Examination …. 13 Teachers’ Council …. 13 Siksha Karmi Union …. 14 Vidyasagar College Students' Union …. 14 Academic Activities …. 15 Laboratories …. 16 Compulsory Computer Awareness Course …. 16 College Library …. 16 Library Rules 16 Seminars …. 17 Counseling Cell …. 17 Grievance Redressal Cell …. 17 Medical and Health Services …. 17 College Computer Centre …. 18 Students' Cheap Store & Canteen …. 18 Ongoing Developmental Activities …. 18 Extra-Curricular Activities …. 18 National Service Scheme …. 18 National Cadet Corp …. 19 Sports and Games …. 19 Social and Cultural Activities …. 19 College Magazine …. 19 General Information …. 20 College Governing Body …. 21 Prizes and Awards …. 22 Faculty Members and Staff …. 23 2 PROSPECTUS 2011 Welcome Vidyasagar College was at the forefront of ushering in a revolution in the field of education in British India. The college, known for its rich, glorious legacy and its immense contribution to the field of education in the country, has its origin in the Metropolitan Training School - later renamed as Calcutta Training School - which was set up by Thakurdas Chakraborty at 1 Arpuly Lane in 1859. In 1860, Vidyasagar became the President of the managing committee of the Training School. In 1864, he was entrusted with the complete charge of its administration and in the same year, he renamed the school as Metropolitan Institution. Vidyasagar sought collegiate affiliation from Calcutta University and the Institution was granted affiliation for First Arts on 1st January, 1872. -

Acharya Prafulla Chandra Ray Nitai Chandra Mandal, FNA Ex-Professor, Department of Biochemistry, Bose Institute, Kolkata
Acharya Prafulla Chandra Ray Nitai Chandra Mandal, FNA Ex-Professor, Department of BioChemistry, Bose Institute, Kolkata Prafulla Chandra Ray was born in the village of Raruli in the District of Jessore (now Khulna) in the then undivided Bengal (now Bangladesh) on August 2, 1861. In the same year, two other great personaliteis, one Rabindranath Tagore was born at Jorasanko, Calcutta, and the other Mr Motilal Nehru was born at Allahabad. Also during the same year, the 81st element in the Mendeleev‟s Periodic Table, Thallium was discovered in the Crook‟s Chemical Laboratory. His father, Harish Chandra Ray was a wealthy land lord, He was the youngest among his brothers. Harish Chandra was a very meritorious student. But, during his study at Krishnanagar College, suddenly his father died. Such circumstance compelled him to discontinue his study and come back to Raruli for taking the responsibility of looking after the Zamindary. He became an active associate of the then New Bengal Movement and engaged himself for the spread of education in his locality. By virtue of his attachment to various federal committees as member, he had close association with many high profile personalities. He was well versed in several languages like English, Parsi, Arabic and Sanskrit. He built a library at home where he kept many books covering all the above languages. Besides, he used to subscribe regularly various News Papers and Magazines So, Prafulla Chandra had the opportunity to utilize this literary environment at home to build the foundation of learning above languages and developing interest in literatures. Through the reading of editorials and criticisms in all those news papers and magazines, he developed the attitude of expressing his personal opinion on any issue, which, actually, was reflected in his various writings in the future. -

The Annual Quality Assurance Report (AQAR) of the IQAC 2014-15
The Annual Quality Assurance Report (AQAR) of the IQAC 2014-15 VIDYASAGAR COLLEGE FOR WOMEN 39, SANKAR GHOSH LANE KOLKATA, WEST BENGAL-700006 AQAR Report: Vidyasagar College for Women: 2014-15 Page 1 The Annual Quality Assurance Report (AQAR) 2014-15 Submitted by Internal Quality Assurance Cell (IQAC) VIDYASAGAR COLLEGE FOR WOMEN 39, SANKAR GHOSH LANE KOLKATA, WEST BENGAL-700006 Submitted to The National Assessment and Accreditation Council (NAAC) Bangalore Contents Part–A Page No. 1. Details of the Institution 3 2. IQAC Composition and Activities 6 Part–B 3. Criterion–I: Curricular Aspects 10 4. Criterion–II: Teaching, Learning and Evaluation 11 5. Criterion–III: Research, Consultancy and Extension 14 6. Criterion–IV: Infrastructure and Learning Resources 20 7. Criterion–V: Student Support and Progression 23 8. Criterion–VI: Governance, Leadership and Management 27 9. Criterion–VII: Innovations and Best Practices 35 10. Annexures 39 AQAR Report: Vidyasagar College for Women: 2014-15 Page 2 The Annual Quality Assurance Report (AQAR) of the IQAC Part – A AQAR for the year 2014-15 1. Details of the Institution 1.1 Name of the Institution VIDYASAGAR COLLEGE FOR WOMEN 1.2 Address Line 1 39, SANKAR GHOSH LANE, KOLKATA WEST BENGAL.PIN-700006 Address Line 2 KOLKATA City/Town KOLKATA WEST BENGAL State Pin Code 700006 [email protected] Institution e-mail address Contact Nos. O33-2241-8887/8889 Dr Rupali Chaudhuri Name of the Head of the Institution: Tel. No. with STD Code: 033-22418887/033-2241-0345 Mobile: 9433177591 AQAR Report: Vidyasagar College for Women: 2014-15 Page 3 Dr Chaitali Basu Name of the IQAC Co-ordinator: Mobile: 9836008693 [email protected] IQAC e-mail address: 1.3 NAAC Track ID OR 1.4 NAAC Executive Committee No. -

Anthropology Arabic Journalism
ANTHROPOLOGY TOTAL GENERAL SC ST OBC(A) OBC(B) PH/VH VACANCY 3 3 4 3 2 0 15 GENERAL University Sl No. College Total CALCUTTA UNIVERSITY 1 BANGABASI COLLEGE (DAY) 1 VIDYASAGAR UNIVERSITY 2 MAHISHADAL GIRLS COLLEGE 1 WEST BENGAL STATE UNIVERSITY 3 MRINALINI DATTA MAHAVIDYAPITH 1 OBC(A) 1 NARASINHA DUTT COLLEGE 1 CALCUTTA UNIVERSITY 2 RAMSADAY COLLEGE 1 VIDYASAGAR UNIVERSITY 3 PRABHAT KUMAR COLLEGE 1 OBC(B) CALCUTTA UNIVERSITY 1 VIVEKANANDA COLLEGE FOR WOMEN 1 WEST BENGAL STATE UNIVERSITY 2 DINABANDHU MAHVIDYALAYA (BONGAON) 1 SC CALCUTTA UNIVERSITY 1 VIVEKANANDA COLLEGE FOR WOMEN 1 2 SITANANDA COLLEGE 1 VIDYASAGAR UNIVERSITY SITANANDA COLLEGE 1 ST CALCUTTA UNIVERSITY 1 BANGABASI MORNING COLLEGE 1 VIDYASAGAR UNIVERSITY 2 PRABHAT KUMAR COLLEGE 1 3 MRINALINI DATTA MAHAVIDYAPITH 1 WEST BENGAL STATE UNIVERSITY 4 SREE CHAITANYA COLLEGE 1 ARABIC TOTAL GENERAL SC ST OBC(A) OBC(B) PH/VH VACANCY 2 2 0 1 1 0 6 GENERAL University Sl No. College Total CALCUTTA UNIVERSITY 1 MAHITOSH NANDI MAHAVIDYALAYA 1 GOURBANGA UNIVERSITY 2 SAMSI COLLEGE 1 OBC(A) KALYANI UNIVERSITY 1 LALGOLA COLLEGE 1 OBC(B) GOURBANGA UNIVERSITY 1 MALDA COLLEGE 1 SC GOURBANGA UNIVERSITY 1 SAMSI COLLEGE 1 KALYANI UNIVERSITY 2 MUZAFFAR AHMED MAHAVIDYALAYA 1 JOURNALISM TOTAL GENERAL SC ST OBC(A) OBC(B) PH/VH VACANCY 1 6 0 4 0 1 12 GENERAL University Sl No. College Total CALCUTTA UNIVERSITY 1 WOMEN'S COLLEGE 1 OBC(A) 1 MAHESHTALA COLLEGE 1 CALCUTTA UNIVERSITY 2 MURALIDHAR GIRLS' COLLEGE 1 3 NETAJINAGAR COLLEGE(EVENING) 1 WEST BENGAL STATE UNIVERSITY 4 BARRAKPORE RASHTRAGURU SURENDRANATH COLLEGE1 PH/VH CALCUTTA UNIVERSITY 1 MAHARAJA MANINDRA CHANDRA COLLEGE 1 SC 1 CHARUCHANDRA COLLEGE 1 CALCUTTA UNIVERSITY 2 NEW ALIPORE COLLEGE 1 3 VIVEKANANDA COLLEGE(THAKURPUKUR) 1 4 ACHARYA PRAFULLA CHANDRA COLLEGE 1 WEST BENGAL STATE UNIVERSITY 5 EAST CALCUTTA GIRLS' COLLEGE 1 6 MRINALINI DATTA MAHAVIDYAPITH 1 GEOLOGY TOTAL GENERAL SC ST OBC(A) OBC(B) PH/VH VACANCY 1 2 0 1 1 0 5 GENERAL University Sl No. -

2017-18) (AQAR) of Internal Quality Assurance Cell (IQAC
VIDYASAGAR UNIVERSITY Midnapore -721 102, West Bengal The Annual Quality Assurance Report (2017-18) (AQAR) of Internal Quality Assurance Cell (IQAC) Submitted to The National Assessment and Accreditation Council Page 1 The Annual Quality Assurance Report (AQAR) of the IQAC (For Universities) Institutions Accredited by NAAC need to submit an Annual self-reviewed progress report i.e. Annual Quality Assurance Report (AQAR) to NAAC, through its IQAC. The report is to detail the tangible results achieved in key areas, specifically identified by the IQAC at the beginning of the Academic year. The AQAR period would be the Academic Year. (For example, July 1, 2017 to June 30, 2018) Part – A Data of the Institution (data may be captured from IIQA) 1. Name of the Institution : Vidyasagar University · Name of the Head of the institution : Dr. Jayanta Kishore Nandi · Designation: Registrar · Does the institution function from · own campus: Yes · Phone no./Alternate Phone No. 03222- 276554 / 276555 / 276557 / 276558 · Mobile No. 9434111115 · Registered Email: [email protected] · Alternate Email : [email protected] · Address : Vidyasagar University, Midnapore , 721 102, Dist- Paschim Medinipur, West Bengal · City/Town : Midnapore · State/UT : West Bengal · Pin Code : 721102 2. Institutional status: · University: State/Central/Deemed/ Private: State University (Tick appropriative) · Type of Institution: Co-education/ Men/Women : Co-education · Location : Rural/Semi-Urban/Urban: Rural Page 2 · Financial Status: Centrally funded/state funded/Private : State Funded (please specify) · Name of the IQAC Co-ordinator/Director: Prof. Prakash C. Dhara · Phone no. /Alternate phone no. : 03222-276554 ext 527 · Mobile: 9433226695 · IQAC E-mail address: [email protected] · Alternate Email address: [email protected] 3. -

VIDYASAGAR COLLEGE 39, Sankar Ghosh Lane Kolkata – 700 006
VIDYASAGAR COLLEGE 39, Sankar Ghosh lane Kolkata – 700 006 www.vidyasagarcollege.edu.in Annual Report 2011 – 2012 A FOREWORD It gives immense pleasure to introduce the Annual Report 2012 of Vidyasagar College aptly named the SPECTRUM. The educational institution named VIDYASAGAR COLLEGE is a living evidence of the fact of history: it truly stood the test of time, spreading the light of education among the people, as thousands of students are shaped every year and are encouraged to go forward to face the realities of life in a befitting manner. This college known for its rich and glorious legacy has thus contributed immensely to the field of education and been in the forefront of the academic arena for over a century and forty years. Very few institutions under the University of Calcutta can claim to such fame. The College has weathered successive storms of social unrest, independence, the birth of a new India, albeit partitioned, the subsequent moribund decades, and then the angry outburst violence as protest of the late 1960s and the 1970s, the restoration of the democratic process of the late 1970s and thence forward, growing all the time, widening its base among the seekers of truth as knowledge, and attracting students and certainly those maestros who take them through the learning process at progressive higher and more complex levels, towards what was and still the very practical and justifiable goal of gainful employment filled with social accountability. This has all been possible because of a solidarity, as the institution as a social organism, is participated in by the teachers, the educational employees, and the stream of students who have and shall inexorably pass through the august pedestals of the College for the founder – the Pundit had been a social engineer and a developer, even an active promoter of both education and social harmony. -

VIDYASAGAR COLLEGE ACCREDITED by NAAC a STAR COLLEGE (DBT, Government of India) 39 Sankar Ghosh Lane Kolkata – 700006
VIDYASAGAR COLLEGE ACCREDITED BY NAAC A STAR COLLEGE (DBT, Government of India) 39 Sankar Ghosh Lane Kolkata – 700006 PROSPECTUS 20133 PROSPECTUS 2013 ACCREDITED BY NAAC VIDYASAGAR COLLEGE 39 SANKAR GHOSH LANE KOLKATA-700006 VIDYASAGAR COLLEGE CONTENT Welcome …. Admission Process …. About the College …. Attendance …. Schedule of College Test and Examination …. Teachers’ Council …. Siksha Karmi Union …. Vidyasagar College Students' Union …. Academic Activities …. Laboratories …. Remedial & Coaching Classes for Entry-in-Service Students Aid Fund College Library …. Library Rules Seminars …. Counseling Cell …. Grievance Redressal Cell …. Medical and Health Services …. College Computer Centre …. Students' Cheap Store & Canteen …. Ongoing Developmental Activities …. Extra-Curricular Activities …. National Service Scheme …. Sports and Games …. Social and Cultural Activities …. College Magazine …. General Information …. College Governing Body …. Prizes and Awards …. Faculty Members and Staff …. List of Holidays 2012-13 …. Academic Calender …. Student Declaration …. 3 PROSPECTUS 20133 Welcome Vidyasagar College was at the forefront of ushering in a revolution in the field of education in British India. The college, known for its rich, glorious legacy and its immense contribution to the field of education in the country, has its origin in the Metropolitan Training School - later renamed as Calcutta Training School - which was set up by Thakurdas Chakraborty at 1 Arpuly Lane in 1859. In 1860, Vidyasagar became the President of the managing committee of the Training School. In 1864, he was entrusted with the complete charge of its administration and in the same year, he renamed the school as Metropolitan Institution. Vidyasagar sought collegiate affiliation from Calcutta University and the Institution was granted affiliation for First Arts on 1st January, 1872. This day is celebrated as the Foundation Day of Vidyasagar College. -

Prof. Malay Mukhopadhyay Professor Department of Geography Visva-Bharati, Santiniketan Present Address: 'Chhauni', West
Prof. Malay Mukhopadhyay Professor Department of Geography Visva-Bharati, Santiniketan Present address: ‘Chhauni’, West Gurupalli, Santiniketan, Pin: 731235 West Bengal, India, Mobile: 9434348167 Email ID: [email protected] Language Skills: Bengali (Native), English (Speaking, Reading and Writing), Hindi (Speaking and Reading) Area of Interest: Environmental Planning, River Management, Tribal Development, Geomorphosite Geo-Tourism Trekked along Five Rivers, Tarafeni (1979), Kopai (1991), Ajay (1995), Mayurakshi # 2000, Thames (2012), Kopai (2017, in celebration of Silver Jubilee) Installation of Marker stone at the source point of River Ajay, 2015 (Saraun Village, Bihar), Kopai River, 2017(Khajuri Village, Jharkhand), Kunur 2018 (Jhanjra Village, West Bengal) Experience in working with Onge, Kani, Apatani and Santhal Tribe of India Qualification: Years Degree College/ University 1975 B.A Vidyasagar college, University of Calcutta 1977 M.A University of Calcutta 1985 Ph.D University of Calcutta Teaching Experience: 32years 2 years (1986-1988) in West Bengal Education Service ( Darjeeling Govt. College ) 30 years (1988-2018) in Visva-Bharati, Department of Geography Member, Professional Development Activities of Academic & Institutional bodies: 1. External Member, Departmental Research Committee, Department of Environmental Science, Kalyani University. 2. External Research Board Member, University of Gour Banga, Malda, West Bengal. 3. Member of Board of Studies, Department of Geography, West Bengal State University, Barasat, West Bengal. 4. External member, Department of Geography, Diamond Harbour Women’s University, South 24 Parganas, West Bengal. 5. Member of the Board of Studies, Department of Geography, Rabindra Bharati University, Kolkata. 6. Member of Board of Studies, Department of Geography, Vidyasagar University, Midnapore, West Bengal. 7. Member of Board of Studies and Ph.D.