The Trend Is Not Your Friend! Why Empirical Timing Success Is Determined by the Underlying's Price Characteristics and Market Efficiency Is Irrelevant
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

ANNA Annual Report.Indd
Association of National Numbering Agencies scrl AAnnualnnual RReporteport 22014013 Contents 3 Chairman’s Report 2014 5 Objectives and mission statements of ANNA 6 General meetings – ANNA administrative review 2014 13 ANNA Service Bureau – report for 2014 14 Securities business and state of ISIN implementation – worldwide 16 Allocation of ISIN for new financial instruments 19 Working Groups, Task Forces and Reginal Groups 25 List of members by COUNTRY as per May 2015 Appendices 29 A ISO 6166 – an outline of the standard 30 B ANNA Guidelines for ISO 6166, Version 12, August 2014 40 C Geographical division of countries among substitute agencies as per May 2015 50 D ISO 10962 – outline of the CFI-(Classification of financial Instruments-) Code 2 www.anna-web.com Chairman’s Report 2014 Dear ANNA Members and Partners, Association strategy, re-evaluating the approved short, medium and long term The year 2014 has been referred to as the direction. Some modifications were made transitionary year from the Age of Recovery to and the Association strategy was presented the Age of Divergence. for validation by the members at the last EGM; Looking at the events of 2014, Central Bank - A growing number of ANNA members actions and divergence have been the under- continued to contribute to the evolution of lying themes. The view remains that these the ISO 17442 – Legal Entity Identifier (LEI) two factors are having and will continue to standard, to promote ANNA’s federated have, significant influence on the global model and the value added benefits of our financial markets and the direction they will model and the National Numbering Agencies take in the near future. -

Final Report Amending ITS on Main Indices and Recognised Exchanges
Final Report Amendment to Commission Implementing Regulation (EU) 2016/1646 11 December 2019 | ESMA70-156-1535 Table of Contents 1 Executive Summary ....................................................................................................... 4 2 Introduction .................................................................................................................... 5 3 Main indices ................................................................................................................... 6 3.1 General approach ................................................................................................... 6 3.2 Analysis ................................................................................................................... 7 3.3 Conclusions............................................................................................................. 8 4 Recognised exchanges .................................................................................................. 9 4.1 General approach ................................................................................................... 9 4.2 Conclusions............................................................................................................. 9 4.2.1 Treatment of third-country exchanges .............................................................. 9 4.2.2 Impact of Brexit ...............................................................................................10 5 Annexes ........................................................................................................................12 -

Doing Data Differently
General Company Overview Doing data differently V.14.9. Company Overview Helping the global financial community make informed decisions through the provision of fast, accurate, timely and affordable reference data services With more than 20 years of experience, we offer comprehensive and complete securities reference and pricing data for equities, fixed income and derivative instruments around the globe. Our customers can rely on our successful track record to efficiently deliver high quality data sets including: § Worldwide Corporate Actions § Worldwide Fixed Income § Security Reference File § Worldwide End-of-Day Prices Exchange Data International has recently expanded its data coverage to include economic data. Currently it has three products: § African Economic Data www.africadata.com § Economic Indicator Service (EIS) § Global Economic Data Our professional sales, support and data/research teams deliver the lowest cost of ownership whilst at the same time being the most responsive to client requests. As a result of our on-going commitment to providing cost effective and innovative data solutions, whilst at the same time ensuring the highest standards, we have been awarded the internationally recognized symbol of quality ISO 9001. Headquartered in United Kingdom, we have staff in Canada, India, Morocco, South Africa and United States. www.exchange-data.com 2 Company Overview Contents Reference Data ............................................................................................................................................ -
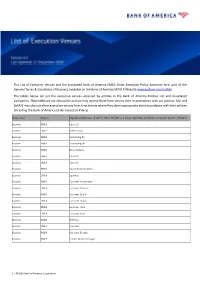
Bofa List of Execution Venues
This List of Execution Venues and the associated Bank of America EMEA Order Execution Policy Summary form part of the General Terms & Conditions of Business available on the Bank of America MifID II Website www.bofaml.com/mifid2 The tables below set out the execution venues accessed by entities in the Bank of America Entities List and Associated Companies. These tables are not exhaustive and we may amend them from time to time in accordance with our policies. MLI and BofASE may also use other execution venues from time to time where they deem appropriate but in accordance with their policies (including the Bank of America Order Execution Policy). Asset class Region Regulated Markets of which MLI / BofASE is a direct member and MTFs accessed by MLI / BofASE Equities EMEA Aquis UK Equities EMEA Athex Group Equities EMEA Bloomberg BV Equities EMEA Bloomberg UK Equities EMEA Borsa Italiana Equities EMEA Cboe BV Equities EMEA Cboe UK Equities EMEA Deutsche Borse Xetra Equities EMEA Equiduct Equities EMEA Euronext Amsterdam Equities EMEA Euronext Brussels Equities EMEA Euronext Dublin Equities EMEA Euronext Lisbon Equities EMEA Euronext Oslo Equities EMEA Euronext Paris Equities EMEA ITG Posit Equities EMEA Liquidnet Equities EMEA Liquidnet Europe Equities EMEA London Stock Exchange 1 – ©2020 Bank of America Corporation Asset class Region Regulated Markets of which MLI / BofASE is a direct member and MTFs accessed by MLI / BofASE Equities EMEA NASDAQ OMX Nordic – Helsinki Equities EMEA NASDAQ OMX Nordic – Stockholm Equities EMEA NASDAQ OMX -
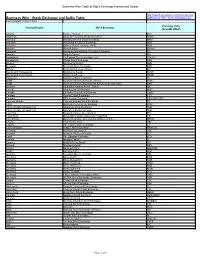
Stock Exchange and Suffix Table Ml/Business Wire Stock Exchanges.Pdf Last Updated 12 March 2021
Business Wire Table of Stock Exchange Names and Usage http://www.businesswire.com/schema/news Business Wire - Stock Exchange and Suffix Table ml/Business_Wire_Stock_Exchanges.pdf Last Updated 12 March 2021 Exchange Value Country/Region Stock Exchange (NewsML ONLY) Albania Bursa e Tiranës BET Argentina Bolsa de Comercio de Buenos Aires BCBA Armenia Nasdaq Armenia Stock Exchange ARM Australia Australian Securities Exchange ASX Australia Sydney Stock Exchange (APX) APX Austria Wiener Börse WBAG Bahamas Bahamas International Securities Exchange BS Bahrain Bahrain Bourse BH Bangladesh Chittagong Stock Exchange, Ltd. CSEBD Bangladesh Dhaka Stock Exchange DSE Belgium Euronext Brussels BSE Bermuda Bermuda Stock Exchange BSX Bolivia Bolsa Boliviana de Valores BO Bosnia and Herzegovina Banjalucka Berza BLSE Bosnia and Herzegovina Sarajevska Berza SASE Botswana Botswana Stock Exchange BT Brazil Bolsa de Valores do Rio de Janeiro BVRJ Brazil Bolsa de Valores, Mercadorias & Futuros de Sao Paulo SAO Bulgaria Balgarska fondova borsa - Sofiya BB Canada Aequitas NEO Exchange NEO Canada Canadian Securities Exchange CNSX Canada Toronto Stock Exchange TSX Canada TSX Venture Exchange TSX VENTURE Cayman Islands Cayman Islands Stock Exchange KY Chile Bolsa de Comercio de Santiago SGO China, People's Republic of Shanghai Stock Exchange SHH China, People's Republic of Shenzhen Stock Exchange SHZ Colombia Bolsa de Valores de Colombia BVC Costa Rica Bolsa Nacional de Valores de Costa Rica CR Cote d'Ivoire Bourse Regionale Des Valeurs Mobilieres S.A. BRVM Croatia -

Nascent Markets: Understanding the Success and Failure of New Stock Markets
Nascent markets: Understanding the success and failure of new stock markets José Albuquerque de Sousa, Thorsten Beck, Peter A.G. van Bergeijk, and Mathijs A. van Dijk* October 2016 Abstract We study the success and failure of 59 newly established (“nascent”) stock markets since 1975 in their first 40 years of activity. Nascent markets differ markedly in their success, as measured by number of listings, market capitalization, and trading activity. Long-term success is in part determined by early success: a high initial number of listings and trading activity are necessary, though not sufficient, conditions for long-term success. Banking sector development at the time of establishment and development of national savings over the life of the stock market are the other two most reliable predictors of success. We find little evidence that structural factors such as legal and political institutions matter. Rather, our results point to an important role of banks, demand factors, and initial scale and success in fostering long-term stock market development. * Albuquerque de Sousa and van Dijk are at the Rotterdam School of Management, Erasmus University. Beck is at Cass Business School, City University London and CEPR. Van Bergeijk is at the International Institute of Social Studies, Erasmus University. E-mail addresses: [email protected], [email protected], [email protected], and [email protected]. We thank Stijn Claessens, Jan Dul, Erik Feyen, Andrei Kirilenko, Thomas Lambert, Roberto Steri (EFA discussant), and seminar participants at the 2016 European Finance Association Meetings, the International Institute of Social Studies, the Netherlands Institute for Advanced Study in the Humanities and Social Sciences, and the Rotterdam School of Management for helpful comments. -

Ebriefing from the CSE
DISTRIBUTED FREE OF CHARGE ebriefing from the CSE CSE monthly electronic edition Promote yourselves in our December 2019 · Issue 275 e-publication The CSE has completely re- Increased Investment Interest at the CSE Roadshow in Athens constructed its on-line publi- cation in order to provide the best possible information to market participants. This newsletter is sent electroni- Important presentations and 70 business meetings cally to thousands of recipi- ents in Cyprus, Greece and by the 6 participating companies abroad. In this context, the The roadshow organised by the CSE in Athens was received with considerable investment CSE has made provision for interest, while the Cyprus and Athens Stock Exchanges reiterated their intention to fur- the promotion of companies through advertising. Any ther enhance the existing close relations between the two organisations. company wishing to promote its products and in the con- text of the upcoming Euro- The roadshow event, held at the offices of the Athens Stock Exchange, began with the pean Union Presidency of the traditional opening bell ceremony and the addresses of Mr. Marinos Christodoulides, Republic of Cyprus during the second half of 2012 and due Chairman of the CSE, and Mr. Socrates Lazaridis, Chief Executive Officer of the Athens to the wide range active par- Stock Exchange. ticipation of the Organization in the European Federations for stock market issues, the In his address, Mr. Lazaridis welcomed the CSE delegation and its companies and referred Cyprus Stock Exchange to the close collaboration between the two stock exchanges in the framework of the (CSE) has undertaken some important initiatives hosting Common Platform. -

The Problem with European Stock Markets
THE PROBLEM WITH EUROPEAN STOCK MARKETS Analysis of the fragmented stock exchange landscape in Europe, how it is holding back growth in capital markets – and what we can do about it March 2021 by William Wright & Eivind Friis Hamre SUMMARY It is not new news that Europe has a complex patchwork of equity markets, stock exchanges and post-trade infrastructure, but this short paper paints this problem in particularly stark terms. The genesis of this paper came from two simple thought experiments: first, can we draw a diagram of the structure of European equity markets on one page? And second, what would the US stock market look like if every state has its own stock exchange? If you read nothing else in this report, please look at the map of the US market on page three and the diagram of European equity markets on page six. Here is a quick summary of this paper: > The elephant in the room The complex patchwork of European equity markets is a huge obstacle to building bigger and better capital markets at a time when the European economy needs them more than ever. We can tinker at the edges with the detail of regulation, but so as long as Europe has 22 different stock exchange groups operating 35 different exchange for listings, 41 exchanges for trading, and nearly 40 different CCPs and CSDs, not much will change. > Punching below its weight The European equity market is less than half the size of the US but has three times as many exchange groups; more than 10 times as many exchanges for listings; more than twice as many exchanges for trading; and roughly 20 times as many post-trade infrastructure providers. -
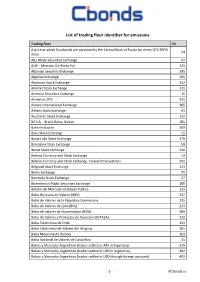
List of Trading Floor Identifier for Emissions
List of trading floor identifier for emissions Trading floor ID A price at which Eurobonds are accepted by the Central Bank of Russia for direct OTC REPO 24 deals Abu Dhabi Securities Exchange 97 AIAF - Mercado De Renta Fija 241 Albanian Secuities Exchange 395 Algerian exchange 291 American Stock Exchange 152 Amman Stock Exchange 311 Armenia Securities Exchange 15 Armenian OTC 331 Astana International Exchange 385 Athens Stock Exchange 53 Australian Stock Exchange 121 B3 S.A. - Brasil, Bolsa, Balcao 181 Bahrain Bourse 309 Baku Stock Exchange 11 Banja Luka Stock Exchange 179 Barcelona Stock Exchange 59 Beirut Stock Exchange 310 Belarus Currency and Stock Exchange 13 Belarus Currency and Stock Exchange. Forward transactions 501 Belgrade Stock Exchange 123 Berlin Exchange 71 Bermuda Stock Exchange 27 Bicentennial Public Securities Exchange 185 Boletin del Mercado de Deuda Publica 113 Bolsa Boliviana de Valores (BBV) 337 Bolsa de Valores de la Republica Dominicana 295 Bolsa de Valores de Lima (BVL) 213 Bolsa de Valores de Mozambique (BVM) 389 Bolsa de Valores y Productos de Asuncion (BVPASA) 313 Bolsa Electronica de Chile 321 Bolsa Electronica de Valores del Uruguay 361 Bolsa Mexicana de Valores 103 Bolsa Nacional de Valores de Costa Rica 31 Bolsas y Mercados Argentinos (trades settled in ARS in Argentina) 379 Bolsas y Mercados Argentinos (trades settled in USD in Argentina) 401 Bolsas y Mercados Argentinos (trades settled in USD through foreign accounts) 403 - 1 - ©Cbonds.ru Trading floor ID BondSpot 69 Borsa Istanbul (International Bonds -

Mean and Variance Causality Between the Cyprus Stock Exchange and Major Equities Markets
Mean and variance causality between the Cyprus Stock Exchange and major equities markets by Eleni Constantinou1*, Robert Georgiades1, Avo Kazandjian2 and Georgios P. Kouretas3** December 2004 Abstract This paper examines the issue of mean and variance causality across four equities markets using daily data for the period 1996-2002. We apply the testing procedure developed by Cheung and Ng (1996) in order to test for mean and variance spillovers. The main findings are: (i) In contrast to the findings of previous studies, EGARCH-M processes characterize each stock returns series in all markets; (ii) There is substantial evidence of causality in both mean and variance with the causality in mean largely being driven by the causality in variance; and (iii) The results indicate the stock markets of Athens, London and New York are the major exporters of causality and the stock market of Cyprus is an importer of causality. Key words: Causality, cross-correlation function, EGARCH-M, equity market, volatility spillovers JEL Classification: C22, C52, G12 1 Department of Accounting and Finance, The Philips College, 4-6 Lamias Street, CY-2100, Nicosia, Cyprus. 2 Department of Business Studies, The Philips College, 4-6 Lamias Street, CY-2100, Nicosia, Cyprus. 3Department of Economics, University of Crete, University Campus, GR-74100, Rethymno, Greece. *This paper is part of the research project, Cyprus Stock Exchange: Evaluation, performance and prospects of an emerging capital market, financed by the Cyprus Research Foundation under research grant Π25/2002. We would like to thank the Cyprus Research Promotion Foundation for its generous financial support and the Cyprus Stock Exchange for proving us with its database. -

Fact Sheets Summary
Fact Sheets Summary Offers Offers Country of Primary Comunications Requires sustainability sustainability Provides Business or Number of Market Cap SSE to environmental guidance or guidance or sustainability Headquarters listed in USD Partner Stakeholders and social training for training for related Has Green Location Stock Exchanges companies millions Exchange sent reporting? companies? investors? indices? Bond Listings Argentina Bolsa de Comercio de Buenos Aire 104 53,105 No No No No No No No Australia Australian Securities Exchange 2048 1,365,958 No No No* No* No No No Austria Wiener Börse AG 104 117,671 No No No No No Yes No Bahrain Bahrain Bourse 46 3,626 No No No No No No No Bermuda Bermuda Stock Exchange 58 1,566 No No No No No No No Brazil BM&FBOVESPA S.A. 366 1,206,426 Yes Yes Yes Yes; Both Yes; Guidance Yes No Canada TMX Group Inc. 3,873 2,113,822 No No Yes Yes; Both Yes; Training Yes No Chile Bolsa de Comercio de Santiago 307 265,150 Yes Yes No* No No No No China Shanghai Stock Exchange 964 2,615,035 No No Yes Yes; Guidance No Yes No China Shenzhen Stock Exchange 1,575 1,452,154 No No No Yes; Guidance No Yes No Colombia Bolsa de Valores de Colombia 74 154,899 Yes Yes No Yes; Training Yes; Guidance No No Cyprus Cyprus Stock Exchange 95 2,105 No No No No No No No Egypt Egyptian Exchange 213 73,372 Yes Yes No No No Yes No Germany Deutsche Börse AG 720 1,936,106 Yes Yes No* Yes; Both No Yes No Greece Athens Exchange Group 251 82,594 No No No No No No No Hong Kong, China Hong Kong Exchanges 1,657 3,100,777 No No No* Yes; Both No No No India BSE India Ltd. -

2018 SSE Report on Progress
The SSE is a UN Partnership Program of: 2018 REPORT ON PROGRESS A paper prepared for the Sustainable Stock Exchanges 2018 Global Dialogue 2018 REPORT ON PROGRESS NOTE Additional substantive contributions were received from Richard Bolwijn (UNCTAD), Danielle Chesebrough The designations employed and the presentation of (PRI & UN Global Compact), Elodie Feller (UNEP FI) the material in this paper do not imply the expression of and Will Martindale (PRI). any opinion whatsoever on the part of the Secretariat of the United Nations concerning the legal status of This paper is presented as an informal contribution any country, territory, city or area, or of its authorities, to the discussions at the SSE Global Dialogue on 23 or concerning the delimitation of its frontiers or October 2018, which takes place within the UNCTAD boundaries. World Investment Forum in Geneva, Switzerland. The views expressed in this paper are those of UNCTAD, This paper is intended for learning purposes. The the UN Global Compact, UN Environment and the PRI inclusion of company names and examples does not unless otherwise stated. constitute an endorsement of the individual exchanges or organisations by the United Nations Conference on The manuscript was edited by Mark Nicholls. The Trade and Development (UNCTAD), the UN Global report was typeset and the charts and infographics Compact, UN Environment or the Principles for designed by Pablo Cortizo. Responsible Investment (PRI). Material in this paper may be freely quoted or reprinted, ABOUT THE SSE but acknowledgement is requested. A copy of the publication containing the quotation or reprint should The SSE initiative is a UN Partnership Programme be sent to [email protected].