DOCSLIB.ORG

Kittitorn Kasemkitwatana //Studies for Project at ENSCI-Les Ateliers

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Kittitorn Kasemkitwatana //Studies for Project at ENSCI-Les Ateliers //kittitorn kasemkitwatana //studies for project at ENSCI-les ateliers //master in Design and contemporary technology (ctc) //subject of impermanence //mathematics and buddhism //e-mail : [email protected] void setup () { size (600,800); } void draw () { //background in black background (0) ; //draw the main circle ellipse (300,300,300,300); stroke (255); fill (0); //draw a series of circles int numberOfcircles=12; float angle=2*PI/numberOfcircles; //repeat for(int i=0;i<numberOfcircles;i++) { float x=300 + 150*cos(angle*i); //calculus of x float y=300 + 150*sin(angle*i); //calculus of x //condition to the width if (i%3==0) { ellipse (x,y,30,30); stroke (255); fill (0); }else{ ellipse (x,y,10,10); stroke (255); fill (0); } } } // p (169); p (168); p // table of content; INTRODUCTION acknowledgement |||||||||||||||||||||||||||||||||||||||6 The nature of reality in a nutshell by religions and mathematics |||||||||||||||||||||||||||||7 james kowall ||||||||||||||||||||||||||||||||||||77 abstract |||||||||||||||||||||||||||||||||||||||||||||17 mathematics and art ||||||||||||||||||||||||||||||||||23 /* Philosophers buddhism thought and mathematics |||||||||||||||||||||24 A metaphysics of morality : Kant and Buddhism |||80 six aspect of mathematics which are relevant to Kant and the moral law ||||||||||||||||||||||||||81 buddhist philosophy ||||||||||||||||||||||||||||||||||26 The connection in terms of principle between philosophers and buddhism |||||||||||||||||||||||88 HISTORY /* Mathematics Buddhism and German Philosophy ||||||||||||||||||92 Euclid ||||||||||||||||||||||||||||||||||||||||||31 Phenomenology and Existentialism ||||||||||||||||94 golden ratio ||||||||||||||||||||||||||||||||||||37 Buddhism and Process philosophy |||||||||||||||||95 physics |||||||||||||||||||||||||||||||||||||||||40 Wittgenstien ||||||||||||||||||||||||||||||||||||96 logic |||||||||||||||||||||||||||||||||||||||||||41 Authur Schopenhauer |||||||||||||||||||||||||||||97 classical Physics |||||||||||||||||||||||||||||||42 Modern Physics ||||||||||||||||||||||||||||||||||43 /* Buddhism and Mathematics Logical forms |||||||||||||||||||||||||||||||||||44 Buddhist Logics ||||||||||||||||||||||||||||||||102 Mathematical logics |||||||||||||||||||||||||||||46 The bodhisattva ideal ||||||||||||||||||||||||||103 Philosophical logics ||||||||||||||||||||||||||||48 Top 10 Mathematical innovations ||||||||||||||||112 Computational logics ||||||||||||||||||||||||||||49 Applied Buddhism in modern mathematics |||||||||115 /* Art and design /* Emptiness The Buddhist concept of ‘Sunyata’ or ‘Emptiness’|118 fashion and textile design ||||||||||||||||||||||52 Evotution of the concept of ‘zero’ in need for mathematics and textiles |||||||||||||||54 modern mathematics |||||||||||||||||||||||||||||119 Buddhist idea in fashion design |||||||||||||||||57 The babylonian system of numerals ||||||||||||||120 Mathematics meet fashion : The evolution of Indian numeral system |||||||||121 Thurston’s concepts inspire designer ||||||||||||59 ‘Zero’ and the place--value notation |||||||||||126 Graphic design and typography |||||||||||||||||||60 Application of ‘emptiness’ in modern mathematics|127 LITERATURE REVIEW Emptiness and null set: the evolution of /* Quantum natural numbers ||||||||||||||||||||||||||||||||129 Quantum and Abhidhamma ||||||||||||||||||||||||||66 Emptiness and null hypothesis ||||||||||||||||||130 Quantum and concept of matter in Abhidhamma |||||68 Quantum Theory and the buddhist concept of /* Forms in buddhism ||||||||||||||||||||||||||||||||133 Dynamic Flux ||||||||||||||||||||||||||||||||||||70 Einstein’s notion of escape velocity and |||||||137 DISCUSSION black holes |||||||||||||||||||||||||||||||||||||71 /* Artist’s work ||||||||||||||||||||||||||||||||||||142 /* Discussion in culture code’s class |||||||||||||||145 Einstein’s view on energy for expanding universe ||||||||||||||||||||||||||||||74 On quantum Theory of consciousness and nature CONCLUSION ||||||||||||||||||||||||||||||||||||||||||||||||151 of reality ||||||||||||||||||||||||||||||||||||||75 BIBLIOGRAPHY ||||||||||||||||||||||||||||||||||||||||||||||158 The universe in composed of that which is aware of WEBOGRAPHY ||||||||||||||||||||||||||||||||||||||||||||||||161 the universe ||||||||||||||||||||||||||||||||||||76 THANK YOU |||||||||||||||||||||||||||||||||||||||||||||||||162 |||||||||||||||||||| // p (5); introduction; p (4); p // acknowledgement religions and mathematics This paper will study the relationship between mathematics and JUDISM religion from the perspective of reason and the role played by Maimonides reason in human knowledge. Firstly, I will study the relation- Moshe ben Maimon, or Mūsā ibn Maymūn, acronymed Rambam , and ship between logic and mathematics. From this starting point, I Graecized (and subsequently Latinized) Moses Maimonides (/ will study the relationship between reason and natural science and maɪˈmɒnɪdiːz/ my--mon--i--deez), a preeminent medieval Sephardic finally, I will draw some conclusions on the relationship between Jewish philosopher and astronomer, became one of the most prolific reason and philosophy. I have an idea from how to use mathematics and influential Torah scholars and physicians of the Middle Ages. and logic to create forms in buddhism and all the topic in this Born in Cordova, Almoravid Empire (present--day Spain) on Passover paper will be the part that helps me explore to work on my final Eve, 1135 or 1138, he died in Egypt on December 12, 1204, whence project. his body was taken to the lower Galilee and buried in Tiberias. He worked as a rabbi, physician, and philosopher in Morocco and Egypt. During his lifetime, most Jews greeted Maimonides’ writings on Jewish law and ethics with acclaim and gratitude, even as far away as Iraq and Yemen, and although Maimonides rose to become the revered head of the Jewish community in Egypt, there were also vociferous critics of some of his writings, particularly in Spain. Nonetheless, he was posthumously acknowledged as among the fore- most rabbinical arbiters and philosophers in Jewish history, and his copious work comprises a cornerstone of Jewish scholarship. His fourteen--volume Mishneh Torah still carries significant ca- nonical authority as a codification of Talmudic law. He is some- times known as “ha Nesher ha Gadol” (the great eagle) in recogni- tion of his outstanding status as a bona fide exponent of the Oral Torah. Aside from being revered by Jewish historians, Maimonides also figures very prominently in the history of Islamic aznd Arab sciences and is mentioned extensively in studies. Influenced by Al--Farabi (ca. 872-950/951), Avicenna (c. 980-1037), and his con- temporary Averroes (1126-1198), he in his turn influenced other prominent Arab and Muslim philosophers and scientists. He became a prominent philosopher and polymath in both the Jewish and Islamic // // worlds. MAIMONIDES A twelfth--century rabbi and community leader, philosopher and physician, Maimonides was fascinated by the relation between sci- ence and religion from his earliest days. A polymath by inclina- p (7); tion, he needed first to master the sciences then extant, includ- p (6); ing logic, mathematics and medicine, before being able to assess LEGAL AND PHILOSOPHICAL WRITINGS their relation to his Jewish faith. Indeed, he insisted on phi- Remarkably, Maimonides continued his education under the stress losophy’s mediating role in the mutual illumination of faith and of exile and travel, composing his commentary on the Jewish le- reason, notably with regard to creation. gal canon, the Mishnah, during the seven years of exile from his twenty--third to thirtieth years. Taking up residence in Fustat EARLY LIFE AND INFLUENCES (Old Cairo), he was appointed judge of the rabbinical court and Mosheh ben Maimon, called Maimonides by Latin authors and known soon assumed leadership of the community. After the death of his to the Arabic--speaking world as Musa ben Maimun, Moses son of brother and the loss of the family savings in a shipwreck, Mai- Maimon, was born on March 30, 1135 c.e., in the city of Córdo- monides took up the responsibility of supporting the family as a ba, Spain, where eight generations of his ancestors had served as physician, practicing medicine until his death. During this time rabbis and rabbinical judges. Capital of the Umayyad emirs and ca- he was court physician to Saladin (c. 1137-1193), the Sultan of liphs in Spain since the eighth century, Córdoba had remained even Egypt and Syria, as well as the entire court, leaving him lit- in their political decline the center of a brilliant, prosperous tle time to study and write, yet he accomplished both, along with civilization in which Jews and Christians, as well as Muslims, adjudicating disputes within the Jewish community. The completion were active participants. Young Moses himself was not to enjoy of his groundbreaking codification of Jewish law, the Mishneh To- this cosmopolitan milieu much past his bar mitzvah, as the fami- rah, around 1178, brought him even greater fame that his earlier ly was forced to flee their home in the wake of the Almohads from commentary, and he was beset with requests for legal opinions from North Africa, who forbade Jews or Christians to profess their re- communities throughout the Islamic world. ligion openly. Yet in the relative calm prior to the shattering of their world, the Jews of Spain had built an intellectual capital At this time, however, he also encountered Rabbi Joseph ibn Judah from which
Load more

Recommended publications
  • Symmetry As an Aesthetic Factor
    Comp. & Maths. with Appls, Vol. 12B, Nos. I/2, pp. 77-82. 1986 0886-9561/86 $3,1)0+ .00 Printed in Great Britain. © 1986 Pergamon Press Ltd. SYMMETRY AS AN AESTHETIC FACTOR HAROLD OSBORNEt Kreutzstrasse 12, 8640 Rappersvill SG, Switzerland Abstract--In classical antiquity symmetry meant commensurability and was believed to constitute a canon of beauty in nature as in art. This intellectualist conception of beauty persisted through the Middle Ages with the addition doctrine that the phenomenal world manifests an imperfect replica of the ideal symmetry of divine Creation. The concept of the Golden Section came to the fore at the Renaissance and has continued as a minority interest both for organic nature and for fine art. The modern idea of symmetry is based more loosely upon the balance of shapes or magnitudes and corresponds to a change from an intellectual to a perceptual attitude towards aesthetic experience. None of these theories of symmetry has turned out to be a principle by following which aesthetically satisfying works of art can be mechanically constructed. In contemporary theory the vaguer notion of organic unity has usurped the prominence formerly enjoyed by that of balanced symmetry. From classical antiquity the idea of symmetry in close conjunction with that of proportion dominated the studio practice of artists and the thinking of theorists. Symmetry was asserted to be the key to perfection in nature as in art. But the traditional concept was radically different from what we understand by symmetry today--so different that "symmetry" can no longer be regarded as a correct translation of the Greek word symmetria from which it derives--and some acquaintance with the historical background of these ideas is essential in order to escape from the imbroglio of confusion which has resulted from the widespread conflation of the two.
    [Show full text]
  • De Divino Errore ‘De Divina Proportione’ Was Written by Luca Pacioli and Illustrated by Leonardo Da Vinci
    De Divino Errore ‘De Divina Proportione’ was written by Luca Pacioli and illustrated by Leonardo da Vinci. It was one of the most widely read mathematical books. Unfortunately, a strongly emphasized statement in the book claims six summits of pyramids of the stellated icosidodecahedron lay in one plane. This is not so, and yet even extensively annotated editions of this book never noticed this error. Dutchmen Jos Janssens and Rinus Roelofs did so, 500 years later. Fig. 1: About this illustration of Leonardo da Vinci for the Milanese version of the ‘De Divina Proportione’, Pacioli erroneously wrote that the red and green dots lay in a plane. The book ‘De Divina Proportione’, or ‘On the Divine Ratio’, was written by the Franciscan Fra Luca Bartolomeo de Pacioli (1445-1517). His name is sometimes written Paciolo or Paccioli because Italian was not a uniform language in his days, when, moreover, Italy was not a country yet. Labeling Pacioli as a Tuscan, because of his birthplace of Borgo San Sepolcro, may be more correct, but he also studied in Venice and Rome, and spent much of his life in Perugia and Milan. In service of Duke and patron Ludovico Sforza, he would write his masterpiece, in 1497 (although it is more correct to say the work was written between 1496 and 1498, because it contains several parts). It was not his first opus, because in 1494 his ‘Summa de arithmetic, geometrica, proportioni et proportionalita’ had appeared; the ‘Summa’ and ‘Divina’ were not his only books, but surely the most famous ones. For hundreds of years the books were among the most widely read mathematical bestsellers, their fame being only surpassed by the ‘Elements’ of Euclid.
    [Show full text]
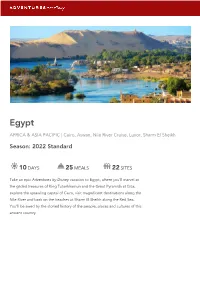
  • 2022 Standard
    EGYPT Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh Egypt AFRICA & ASIA PACIFIC | Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh Season: 2022 Standard 10 DAYS 25 MEALS 22 SITES Take an epic Adventures by Disney vacation to Egypt, where you’ll marvel at the gilded treasures of King Tutankhamun and the Great Pyramids at Giza, explore the sprawling capital of Cairo, visit magnificent destinations along the Nile River and bask on the beaches at Sharm El Sheikh along the Red Sea. You’ll be awed by the storied history of the people, places and cultures of this ancient country. EGYPT Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh Trip Overview 10 DAYS / 9 NIGHTS ACCOMMODATIONS 5 LOCATIONS The Nile Ritz-Carlton, Cairo Cairo, Aswan, Nile River M/S Tulip Cruise, Luxor, Sharm El Sheikh Coral Sea Sensatori Resort AGES FLIGHT INFORMATION 25 MEALS Minimum Age: 6 Arrive: Cairo International 9 Breakfasts, 8 Lunches, 8 Suggested Age: 8+ Airport (CAI) Dinners Adult Exclusive: Ages 18+ Return: Cairo International Airport (CAI) All Internal Flights Included EGYPT Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh DAY 1 CAIRO Activities Highlights: No Meals Included Arrive in Cairo The Nile Ritz-Carlton, Cairo Arrive in Cairo ‘Ahlaan Wasahlaan Bikum! Upon your arrival at Cairo International Airport, Adventures by Disney Guests will be escorted to a VIP lounge while your passports are processed and your luggage is reclaimed. You will then be taken to your waiting vehicles for transfer to the hotel, The Nile Ritz-Carlton, Cairo. The Nile Ritz-Carlton, Cairo Bask in the elegance that surrounds you in this luxury hotel that offers world-class services and amenities that are fit for a pharaoh.
    [Show full text]
  • EGYPT – PRIVATE ADVENTURE Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh
    EGYPT – PRIVATE ADVENTURE Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh Egypt – Private Adventure AFRICA & ASIA PACIFIC | Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh Season: 2021 10 DAYS 25 MEALS 22 SITES Take an epic Adventures by Disney Private Adventure to Egypt, where you’ll marvel at the gilded treasures of King Tutankhamun and the Great Pyramids at Giza, explore the sprawling capital of Cairo, visit magnificent destinations along the Nile River and bask on the beaches at Sharm El Sheikh along the Red Sea. You’ll be awed by the storied history of the people, places and cultures of this ancient country. EGYPT – PRIVATE ADVENTURE Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh Trip Overview 10 DAYS / 9 NIGHTS ACCOMMODATIONS 5 LOCATIONS The Nile Ritz-Carlton, Cairo Cairo, Aswan, Nile River M/S Tulip Cruise, Luxor, Sharm El Sheikh Coral Sea Sensatori Resort AGES FLIGHT INFORMATION 25 MEALS Minimum Age: None Arrive: Cairo International 9 Breakfasts, 8 Lunches, 8 Airport (CAI) Dinners Return: Cairo International Airport (CAI) All Internal Flights Included EGYPT – PRIVATE ADVENTURE Cairo, Aswan, Nile River Cruise, Luxor, Sharm El Sheikh DAY 1 CAIRO Activities Highlights: No Meals Included Arrive in Cairo The Nile Ritz-Carlton, Cairo Arrive in Cairo ‘Ahlaan Wasahlaan Bikum! Upon your arrival at Cairo International Airport, Adventures by Disney Guests will be escorted to a VIP lounge while your visa and passports are processed and your luggage is reclaimed. You will then be taken to your waiting vehicle for transfer to the hotel, The Nile Ritz-Carlton, Cairo. Note: A visa is provided to each Guest upon arrival and does not need to be secured in advance of departing for Egypt.
    [Show full text]
  • The Mars Pentad Time Pyramids the Quantum Space Time Fractal Harmonic Codex the Pentagonal Pyramid
    The Mars Pentad Time Pyramids The Quantum Space Time Fractal Harmonic Codex The Pentagonal Pyramid Abstract: Early in this author’s labors while attempting to create the original Mars Pentad Time Pyramids document and pyramid drawings, a failure was experienced trying to develop a pentagonal pyramid with some form of tetrahedral geometry. This pentagonal pyramid is now approached again and refined to this tetrahedral criteria, creating tetrahedral angles in the pentagonal pyramid, and pentagonal [54] degree angles in the pentagon base for the pyramid. In the process another fine pentagonal pyramid was developed with pure pentagonal geometries using the value for ancient Egyptian Pyramid Pi = [22 / 7] = [aPi]. Also used is standard modern Pi and modern Phi in one of the two pyramids shown. Introduction: Achieved are two Pentagonal Pyramids: One creates tetrahedral angle [54 .735~] in the Side Angle {not the Side Face Angle}, using a novel height of the value of tetrahedral angle [19 .47122061] / by [5], and then the reverse tetrahedral angle is accomplished with the same tetrahedral [19 .47122061] angle value as the height, but “Harmonic Codexed” to [1 .947122061]! This achievement of using the second height mentioned, proves aspects of the Quantum Space Time Fractal Harmonic Codex. Also used is Height = [2], which replicates the [36] and [54] degree angles in the pentagon base to the Side Angles of the Pentagonal Pyramid. I have come to understand that there is not a “perfect” pentagonal pyramid. No matter what mathematical constants or geometry values used, there will be a slight factor of error inherent in the designs trying to attain tetrahedra.
    [Show full text]
  • Simple Rules for Incorporating Design Art Into Penrose and Fractal Tiles
    Bridges 2012: Mathematics, Music, Art, Architecture, Culture Simple Rules for Incorporating Design Art into Penrose and Fractal Tiles San Le SLFFEA.com [email protected] Abstract Incorporating designs into the tiles that form tessellations presents an interesting challenge for artists. Creating a viable M.C. Escher-like image that works esthetically as well as functionally requires resolving incongruencies at a tile’s edge while constrained by its shape. Escher was the most well known practitioner in this style of mathematical visualization, but there are significant mathematical objects to which he never applied his artistry including Penrose Tilings and fractals. In this paper, we show that the rules of creating a traditional tile extend to these objects as well. To illustrate the versatility of tiling art, images were created with multiple figures and negative space leading to patterns distinct from the work of others. 1 1 Introduction M.C. Escher was the most prominent artist working with tessellations and space filling. Forty years after his death, his creations are still foremost in people’s minds in the field of tiling art. One of the reasons Escher continues to hold such a monopoly in this specialty are the unique challenges that come with creating Escher type designs inside a tessellation[15]. When an image is drawn into a tile and extends to the tile’s edge, it introduces incongruencies which are resolved by continuously aligning and refining the image. This is particularly true when the image consists of the lizards, fish, angels, etc. which populated Escher’s tilings because they do not have the 4-fold rotational symmetry that would make it possible to arbitrarily rotate the image ± 90, 180 degrees and have all the pieces fit[9].
    [Show full text]
  • Syddansk Universitet Review of "Henning, Herbert: La Divina
    Syddansk Universitet Review of "Henning, Herbert: La divina proportione und die Faszination des Schönen oder das Schöne in der Mathematik" Robering, Klaus Published in: Mathematical Reviews Publication date: 2014 Document version Accepted author manuscript Citation for pulished version (APA): Robering, K. (2014). Review of "Henning, Herbert: La divina proportione und die Faszination des Schönen oder das Schöne in der Mathematik". Mathematical Reviews. General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal ? Take down policy If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. Download date: 14. Feb. 2017 MR3059375 Henning, Herbert La divina proportione und die Faszination des Sch¨onenoder das Sch¨onein der Mathematik. (German) [The divine proportion and the fascination of beauty or beauty in mathematics] Mitt. Math. Ges. Hamburg 32 (2012), 49{62 00A66 (11B39 51M04) The author points out that there is a special relationship between mathematics and the arts in that both aim at the discovery and presentation of truth and beauty.
    [Show full text]
  • Leonardo Universal
    Leonardo Universal DE DIVINA PROPORTIONE Pacioli, legendary mathematician, introduced the linear perspective and the mixture of colors, representing the human body and its proportions and extrapolating this knowledge to architecture. Luca Pacioli demonstrating one of Euclid’s theorems (Jacobo de’Barbari, 1495) D e Divina Proportione is a holy expression commonly outstanding work and icon of the Italian Renaissance. used in the past to refer to what we nowadays call Leonardo, who was deeply interested in nature and art the golden section, which is the mathematic module mathematics, worked with Pacioli, the author of the through which any amount can be divided in two text, and was a determined spreader of perspectives uneven parts, so that the ratio between the smallest and proportions, including Phi in many of his works, part and the largest one is the same as that between such as The Last Supper, created at the same time as the largest and the full amount. It is divine for its the illustrations of the present manuscript, the Mona being unique, and triune, as it links three elements. Lisa, whose face hides a perfect golden rectangle and The fusion of art and science, and the completion of the Uomo Vitruviano, a deep study on the human 60 full-page illustrations by the preeminent genius figure where da Vinci proves that all the main body of the time, Leonardo da Vinci, make it the most parts were related to the golden ratio. Luca Pacioli credits that Leonardo da Vinci made the illustrations of the geometric bodies with quill, ink and watercolor.
    [Show full text]
  • Kepler's Cosmos
    science and image Kepler’s cosmos Copernicus’s system of the Universe was revolutionary but his method of representing it on paper was anything but. It was left to Kepler to apply Renaissance techniques of spatial visualization to make the theory come alive. Martin Kemp icolaus Copernicus’s programme to 8 purge the Ptolemaic model of the Uni- Nverse of its growing burden of disfig- uring complications was driven not least by what we would call aesthetic considerations. The architecture of his heliocentric system reinstated the geometrical integrity that the Greek astronomers had sought: “At rest... in the middle of everything is the sun. For in this most beautiful temple, who would place this lamp in another or better position than that from which it can light up the whole thing at the same time?” Although Copernicus’s “temple” obeyed the principles of harmonically unified design advocated in the Renaissance, his conventionally diagrammatic representa- tion of his scheme in 1543 as a flat series of concentric circles did not avail itself of the new spatial vision inherent in the buildings and paintings of the Renaissance masters. It was more than 50 years later that Johannes Kepler, fervent Copernican and Platonist, allied the new visual forms with the new astronomical vision. Among the many testimonies to Kepler’s extraordinary powers of spatial visualiza- tion, none is more remarkable than the great cosmological model he illustrated in a fold- out plate in his Mysterium Cosmographicum of 1596. We know how the scheme came to be envisaged. He tells how, when he was teach- ing his “students the way Great Conjunc- tions jump eight signs at a time”, he drew Kepler’s “Model of the Orbits of the Planets” “many triangles, or quasi triangles, in the from Mysterium Cosmographicum, 1596 (above).
    [Show full text]
  • Art and Anatomy: the Vitruvian Teen
    Curriculum Units by Fellows of the Yale-New Haven Teachers Institute 2006 Volume VI: Anatomy and Art: How We See and Understand Art and Anatomy: The Vitruvian Teen Curriculum Unit 06.06.01 by Wendy Decter, M.D. Justification Ultimately, learning becomes interdisciplinary as we mature and have opportunities for varied experiences. As adults and teachers it is our responsibility to facilitate growth and provide opportunity for different experiences. Meaningful interpretation and integration of experience must be modeled for our students as well. In grade school children build reading, writing, computational and analytical skills in a step by step fashion usually with one teacher each year. The next teacher uses the previous years' accomplishments as building blocks. Gradually vocabulary expands and students read more complex books. Perspective expands as we start to learn about countries and cultures other than our own, and examine the physical world around us. A sense of community and of the value of education is a necessary ingredient, both in school and at home. Throughout the grades, our students' required readings are set in the historical setting that is being explored from a social standpoint. Our students are acquiring the computational skills needed in their current scientific studies. They move from learning about their town, to their state, to their country and finally to their world and beyond. In middle school and high school courses and the school day becomes compartmentalized. English, now dubbed Language Arts, Social Studies, Science, Math, Art, and Foreign Language are separate departments with differentiated courses taught by many teachers in many ways.
    [Show full text]
  • The Deep Space Mission That Might Trigger a Multidisciplinary Scientific Revolution by Judy Hodgkiss
    II. Scientific Revolutions Will Shape the Future The Deep Space Mission that Might Trigger a Multidisciplinary Scientific Revolution by Judy Hodgkiss President Trump insists he wants the U.S. to lead Is There a Fundamental Principle of the world in scientific and technological develop- Development in the Universe? ment. He instinctively understands that the key to In 1921, Albert Einstein went beyond his relativity doing that is resuscitating and upgrading the U.S. theory, and put forward a theory of the cosmos, what he space program. called the concept of a “finite but unbounded” universe. As an example of the fundamentals of physical In a lecture that year before the Prussian Academy of economy, Lyndon LaRouche frequently pointed out Sciences, he asked the audience to consider a new met- how John F. Kennedy’s Apollo Project space mission aphor: He described the physical universe as a finite had provided the impetus for explosive growth of the number of shadows projected from different kinds of “Silicon Valley,” the previously higher-order geometries. He chal- bucolic rural area near San Jose, lenged the audience to not only California, which became Ameri- imagine the unseen geometries, ca’s high-tech center in the 1960s. but to imagine novel yardsticks LaRouche always insisted that that could measure them. Such a space exploration must be the universe would be bound only by point-on-the-spear in terms of the principles of development that scientific R&D. If the nation’s characterized it.1 frontier missions in space are ap- Einstein would be delighted propriately defined and fully- today to see examples of scien- funded, they not only provide tists in such fields as physics, spin-off benefits in innovative chemistry, or electronics, discov- ALMA technologies in obviously related Proto-planetary disc surrounding the young ering, to their amazement, that fields, but, even more impor- stellar object, Elias 2-27, 450 light-years away.
    [Show full text]
  • Seven Wonders Time:​ 30 Minutes Level:​ Beginner
    Lesson Five: Seven Wonders Time:​ 30 minutes Level:​ Beginner Intro The Seven Wonders of the Ancient World were architectural feats recorded by ancient historians, writers and scholars in the western world - the list is limited geographically to the mediterranean, the centre of ancient western civilization. The only remaining wonder in the present day is the Great Pyramid of Giza, which is also the oldest. The rest have all been destroyed by weather, war or nature. Today we’re going to learn a little bit about each one: The Great Pyramid of Giza The pyramids are, in many ways, the most famous ancient wonder of the world. Whether that’s attributed to their mystery, incredible feat of construction, or their sole survival (out of all of the ancient wonders) into the modern era, all marvel at their magnificence. The Great Pyramid of Giza was constructed around 2589-2566 B.C. during the reign of Pharaoh Khufu. It stood about 147 meters tall and its base was approximately 230 meters in length. The second pyramid was created for Khufu’s son, Pharaoh Khafre, in 2558-2532 B.C. Within the pyramid’s complex at Giza was the largest statue in the world at that time, known as the Great Sphinx (a man’s head on a lion’s body), standing 240 feet long and 66 feet tall. The last pyramid was built around 2532-2503 B.C. for Khafre’s son, Pharaoh Menkaure. It was the shortest of the three pyramids in this ancient wonder, standing at only 216 feet tall. It took over 2.3 million blocks of limestone, 100,000 men, and 20 years to construct the greatest architectural achievement in the ancient world.
    [Show full text]