PDF, the Black Hole Mass in the Brightest Cluster Galaxy NGC 6086
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Interstellarum 40 Erreicht Die Heftzahl Der Neuen Folge Nun Gleich- Stand Mit Den Ausgaben Der Früheren Deep-Sky-Zeitschrift
fokussiert Liebe Leserinnen, liebe Leser, 20 Hefte Zeitschrift für praktische Astronomie Als interstellarum sich mit der Ausgabe 20 vom »Magazin für Deep-Sky- Beobachter« zur »Zeitschrift für praktische Astronomie« wandelte, gab es nicht nur positive Kommentare, wie die Leserbriefe in Heft 21 zeigten. Mit interstellarum 40 erreicht die Heftzahl der neuen Folge nun Gleich- stand mit den Ausgaben der früheren Deep-Sky-Zeitschrift. Im Rückblick zeigt sich, wie richtig der damals auch in der Redaktion viel diskutierte Schritt war: interstellarum konnte seine Aufl age seit 2001 vervierfachen. Für Heft 40 wurde diese noch einmal erhöht – diese Ausgabe geht mit knapp 9000 Heften in den Handel. Dort ist interstellarum inzwischen in Deutschland, Österreich, der Schweiz und Italien am Kiosk erhältlich. Astrofotografen für interstellarum Einen besonderen Anteil am Erfolg von interstellarum haben die zahl- reichen Astrofotografen, die die Illustration jeder Ausgabe mit großarti- gen Fotos ermöglichen. Um ihr Engagement zu honorieren, heben wir ab sofort die Namen derjenigen Astrofotografen im Impressum (Seite 78) hervor, die interstellarum regelmäßig ihre Aufnahmen einsenden. Die Redaktion möchte damit auch andere führende Astrofotografen einla- den, ihre Bildergebnisse der Zeitschrift zur Verfügung zu stellen. Weitere Informationen zu unserem Angebot für Astrofotografen können Sie im Internet unter www.interstellarum.de nachlesen. Stefan Seip Südhimmel-Sehnsucht Das Kreuz des Südens, Omega Centauri, die Magellanschen Wolken – wer träumt nicht von einer Exkursion zu den spektakulären Zielen des südlichen Sternhimmels, die bei uns immer unsichtbar bleiben? In einem zweiteiligen Artikel huldigen wir dem Südhimmel und seinen schönsten Deep-Sky-Objekten mit Astrofotos und Zeichnungen gleichermaßen. Las- sen Sie sich vom Südhimmel-Virus anstecken und mitnehmen auf eine Reise zu Katzenpfoten, Kohlensack und Käfernebel (Seite 50). -

Two Ten-Billion-Solar-Mass Black Holes at the Centres of Giant Elliptical Galaxies
LETTER doi:10.1038/nature10636 Two ten-billion-solar-mass black holes at the centres of giant elliptical galaxies Nicholas J. McConnell1, Chung-Pei Ma1, Karl Gebhardt2, Shelley A. Wright1, Jeremy D. Murphy2, Tod R. Lauer3, James R. Graham1,4 & Douglas O. Richstone5 Observational work conducted over the past few decades indicates (Figs 1 and 2). We determined the mass of the central black hole by that all massive galaxies have supermassive black holes at their constructing a series of orbit superposition models12. Each model centres. Although the luminosities and brightness fluctuations of assumes a black-hole mass, stellar mass-to-light ratio and dark-matter quasars in the early Universe suggest that some were powered by profile, and generates a library of time-averaged stellar orbits in the black holes with masses greater than 10 billion solar masses1,2, the resulting gravitational potential. The model then fits a weighted com- remnants of these objects have not been found in the nearby bination of orbital line-of-sight velocities to the set of measured stellar Universe. The giant elliptical galaxy Messier 87 hosts the hitherto velocity distributions. The goodness-of-fit statistic x2 is computed as a most massive known black hole, which has a mass of 6.3 billion function of the assumed values of MBH and the stellar mass-to-light solar masses3,4. Here we report that NGC 3842, the brightest galaxy ratio. Using our best-fitting model dark-matter halo, we measure a 9 in a cluster at a distance from Earth of 98 megaparsecs, has a central black-hole mass of 9.7 3 10 solar masses (M8), with a 68% con- 9 black hole with a mass of 9.7 billion solar masses, and that a black fidence interval of (7.2–12.7) 3 10 M8. -

Ngc Catalogue Ngc Catalogue
NGC CATALOGUE NGC CATALOGUE 1 NGC CATALOGUE Object # Common Name Type Constellation Magnitude RA Dec NGC 1 - Galaxy Pegasus 12.9 00:07:16 27:42:32 NGC 2 - Galaxy Pegasus 14.2 00:07:17 27:40:43 NGC 3 - Galaxy Pisces 13.3 00:07:17 08:18:05 NGC 4 - Galaxy Pisces 15.8 00:07:24 08:22:26 NGC 5 - Galaxy Andromeda 13.3 00:07:49 35:21:46 NGC 6 NGC 20 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 7 - Galaxy Sculptor 13.9 00:08:21 -29:54:59 NGC 8 - Double Star Pegasus - 00:08:45 23:50:19 NGC 9 - Galaxy Pegasus 13.5 00:08:54 23:49:04 NGC 10 - Galaxy Sculptor 12.5 00:08:34 -33:51:28 NGC 11 - Galaxy Andromeda 13.7 00:08:42 37:26:53 NGC 12 - Galaxy Pisces 13.1 00:08:45 04:36:44 NGC 13 - Galaxy Andromeda 13.2 00:08:48 33:25:59 NGC 14 - Galaxy Pegasus 12.1 00:08:46 15:48:57 NGC 15 - Galaxy Pegasus 13.8 00:09:02 21:37:30 NGC 16 - Galaxy Pegasus 12.0 00:09:04 27:43:48 NGC 17 NGC 34 Galaxy Cetus 14.4 00:11:07 -12:06:28 NGC 18 - Double Star Pegasus - 00:09:23 27:43:56 NGC 19 - Galaxy Andromeda 13.3 00:10:41 32:58:58 NGC 20 See NGC 6 Galaxy Andromeda 13.1 00:09:33 33:18:32 NGC 21 NGC 29 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 22 - Galaxy Pegasus 13.6 00:09:48 27:49:58 NGC 23 - Galaxy Pegasus 12.0 00:09:53 25:55:26 NGC 24 - Galaxy Sculptor 11.6 00:09:56 -24:57:52 NGC 25 - Galaxy Phoenix 13.0 00:09:59 -57:01:13 NGC 26 - Galaxy Pegasus 12.9 00:10:26 25:49:56 NGC 27 - Galaxy Andromeda 13.5 00:10:33 28:59:49 NGC 28 - Galaxy Phoenix 13.8 00:10:25 -56:59:20 NGC 29 See NGC 21 Galaxy Andromeda 12.7 00:10:47 33:21:07 NGC 30 - Double Star Pegasus - 00:10:51 21:58:39 -

Kinematics and Stellar Populations in Brightest Cluster Galaxies
KINEMATICS AND STELLAR POPULATIONS IN BRIGHTEST CLUSTER GALAXIES Susan Ilani Loubser A THESIS SUBMITTED IN PARTIAL FULFILMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY Jeremiah Horrocks Institute for Astrophysics and Supercomputing School of Computing, Engineering and Physical Sciences University of Central Lancashire June 2009 uclan Iinlvenity of Central Lancashire Student Declaration Concurrent registration for two or more academic awards I declare that while registered as a candidate for the research degree. I have not been a registered candidate or enrolled student for another award of the University or other academic or professional Institution Material submitted for another award I declare that no material contained in the thesis has been used In any other submission for an academic award and Is solely my own work Collaboration Where a candidates research programme is part of a collaborative project, the thesis must indicate In addition clearly the candidate's individual contribution and the extent of the collaboration. Please state below: The entire thesis is the work of the candidate, Susan Ilani Loubser. Signature of Candidate Type of Award Doctor of Philosophy School School of Computing, Engineering and Physical Sciences Abstract This thesis is devoted to the investigation of a new, large sample of brightest cluster galaxies (BOGs), their kinematic and stellar population properties and the relationships between these and the properties of the host clusters. Some of the questions addressed are: how the kinematic and stellar population properties differ from those of ordinary giant elliptical galaxies; and whether these properties are more influenced by the internal parameters of the BOGs or the properties of the host clusters. -

Super-Massive Black Hole Scaling Relations and Peculiar Ringed Galaxies
SUPER-MASSIVE BLACK HOLE SCALING RELATIONS AND PECULIAR RINGED GALAXIES A DISSERTATION SUBMITTED TO THE FACULTY OF THE GRADUATE SCHOOL OF THE UNIVERSITY OF MINNESOTA BY BURCIN MUTLU IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY MARC S. SEIGAR June, 2017 c BURCIN MUTLU 2017 ALL RIGHTS RESERVED Acknowledgements There are several people who I would like to acknowledge for directly or indirectly contributing to this dissertation. First and foremost, I would like to acknowledge the guidance and support of my ad- visor, Marc S. Seigar. I am thankful to him for his continuous encouragement, patience, and kindness. I appreciate all his contributions of knowledge, expertise, and time, which were invaluable to my success in graduate school. He has set an example of excellence as a researcher, mentor, and role model. In addition, I would like to thank my dissertation committee, Liliya L. R. Williams, M. Claudia Scarlata, and Robert Lysak, for their insightful input, constructive criticism and direction during the course of this dissertation. I have crossed paths with many collaborators who have influenced and enhanced my research. Patrick Treuthardt has been a collaborator for most of the work during my dissertation. The addition of his scientific point of view has improved the quality of the work in this dissertation tremendously. Our discussions have always been stimulating and rewarding. I am thankful to him for mentoring me and being a dear friend to me. I would also like to thank Benjamin L. Davis for numerous helpful advice and inspiring discussions. He has directly involved with many aspects of Chapter 1. -

Annual Report 2011
ANNUAL REPORT 2011 ON THE COVER: HEADQUARTERS LOCATION: FY2011 Ace summit operations team Kamuela, Hawai’i, USA Number of Full Time members, from left: Arnold Employees: 115 Matsuda, John Baldwin and MANAGEMENT: Mike Dahler, focus their California Association for Number of Observing attention to removing a Research in Astronomy Astronomers FY2011: 464 single segment from the PARTNER INSTITUTIONS: Number of Keck Science Keck Telescope primary California Institute of Investigations: 400 mirror in the first major step Technology (CIT/Caltech), in the segment recoating Number of Refereed Articles process. University of California (UC), FY2011: 278 National Aeronautics and Fiscal Year begins October 1 BELOW: Space Administration (NASA) The newly commissioned Federal Identification Keck I Laser penetrates the OBSERVATORY DIRECTOR: Number: 95-3972799 night sky from the majestic Taft E. Armandroff landscape of Mauna Kea. DEPUTY DIRECTOR: The laser is part of Keck’s Hilton A. Lewis world leading adaptive optics systems, a technology used to remove the effects of turbulence in Earth’s atmosphere and provides unprecedented image clarity of cosmic targets near and distant. VISION A world in which all humankind is inspired and united by the pursuit of knowledge of the infinite CONTENTS variety and richness of the Universe. Director’s Report . 3 Cosmic Visionaries . 6 Science Highlights . 8 MISSION Finances . 16 To advance the frontiers of astronomy and share Philanthropic Support . .18 our discoveries, inspiring the imagination of all. Reflections . .20 Education & Outreach . .22 Observatory Groundbreaking: 1985 Honors & Recognition . .26 First light Keck I telescope: 1992 Science Bibliography . 28 First light Keck II telescope: 1996 DIRECTOR’s REPORT Taft E. -
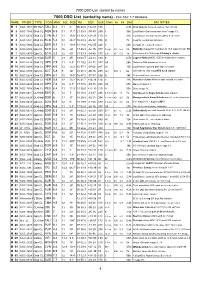
DSO List V2 Current
7000 DSO List (sorted by name) 7000 DSO List (sorted by name) - from SAC 7.7 database NAME OTHER TYPE CON MAG S.B. SIZE RA DEC U2K Class ns bs Dist SAC NOTES M 1 NGC 1952 SN Rem TAU 8.4 11 8' 05 34.5 +22 01 135 6.3k Crab Nebula; filaments;pulsar 16m;3C144 M 2 NGC 7089 Glob CL AQR 6.5 11 11.7' 21 33.5 -00 49 255 II 36k Lord Rosse-Dark area near core;* mags 13... M 3 NGC 5272 Glob CL CVN 6.3 11 18.6' 13 42.2 +28 23 110 VI 31k Lord Rosse-sev dark marks within 5' of center M 4 NGC 6121 Glob CL SCO 5.4 12 26.3' 16 23.6 -26 32 336 IX 7k Look for central bar structure M 5 NGC 5904 Glob CL SER 5.7 11 19.9' 15 18.6 +02 05 244 V 23k st mags 11...;superb cluster M 6 NGC 6405 Opn CL SCO 4.2 10 20' 17 40.3 -32 15 377 III 2 p 80 6.2 2k Butterfly cluster;51 members to 10.5 mag incl var* BM Sco M 7 NGC 6475 Opn CL SCO 3.3 12 80' 17 53.9 -34 48 377 II 2 r 80 5.6 1k 80 members to 10th mag; Ptolemy's cluster M 8 NGC 6523 CL+Neb SGR 5 13 45' 18 03.7 -24 23 339 E 6.5k Lagoon Nebula;NGC 6530 invl;dark lane crosses M 9 NGC 6333 Glob CL OPH 7.9 11 5.5' 17 19.2 -18 31 337 VIII 26k Dark neb B64 prominent to west M 10 NGC 6254 Glob CL OPH 6.6 12 12.2' 16 57.1 -04 06 247 VII 13k Lord Rosse reported dark lane in cluster M 11 NGC 6705 Opn CL SCT 5.8 9 14' 18 51.1 -06 16 295 I 2 r 500 8 6k 500 stars to 14th mag;Wild duck cluster M 12 NGC 6218 Glob CL OPH 6.1 12 14.5' 16 47.2 -01 57 246 IX 18k Somewhat loose structure M 13 NGC 6205 Glob CL HER 5.8 12 23.2' 16 41.7 +36 28 114 V 22k Hercules cluster;Messier said nebula, no stars M 14 NGC 6402 Glob CL OPH 7.6 12 6.7' 17 37.6 -03 15 248 VIII 27k Many vF stars 14.. -

Tod R. Lauer Publications in Refereed Journals 1. an Analysis of the Spectra of the Seyfert Galaxies Markarian 79 and I Zw 1
Tod R. Lauer Publications in Refereed Journals 1. An Analysis of the Spectra of the Seyfert Galaxies Markarian 79 and I Zw 1. (1979), ApJ, 230, 360. J. B. Oke & T. R. Lauer. 2. Speckle Interferometric Observations of Pluto and Charon. (1982), Icarus, 50, 72. E. K. Hege, E. N. Hubbard, J. D. Drummond, P. A. Strittmatter, S. P. Worden, & T. R. Lauer. 3. High Resolution Surface Photometry of Elliptical Galaxies. (1985), ApJS, 57, 473. T. R. Lauer. 4. The Cores of Elliptical Galaxies. (1985), ApJ, 292, 101. T. R. Lauer. 5. Boxy Isophotes, Disks, and Dust Lanes in Elliptical Galaxies. (1985), MN- RAS, 216, 429. T. R. Lauer. 6. The Core of the M87 Globular Cluster System. (1986), ApJ, 303, L1. T. R. Lauer & J. Kormendy. 7. Photometric Decomposition of the Multiple-Nucleus Galaxy NGC 6166. (1986), ApJ, 311, 34. T. R. Lauer. 8. The Morphology of Multiple-Nucleus Brightest Cluster Galaxies. (1988), ApJ, 325, 49. T. R. Lauer. 9. The Far-Ultraviolet Spectra of Early-Type Galaxies. (1988), ApJ, 328, 440. D. Burstein, F. Bertola, L. M. Buson, S. M. Faber, & T. R. Lauer. 10. An Optical Detection and Characterization of the Eclipsing Pulsar’s Com- panion. (1988), Nat, 334, 686. A. S. Fruchter, J. E. Gunn, T. R. Lauer, & A. Dressler. 11. The Reduction of Wide Field/Planetary Camera Images. (1989), PASP, 101, 445. T. R. Lauer. 12. Core Expansion in LMC Clusters. (1989), ApJ, 347, L69. R. A. W. Elson, K. C. Freeman, & T. R. Lauer. 13. Stellar Photometry with the Hubble Space Telescope Wide Field/Planetary Camera: A Progress Report. -

Arxiv:2012.04471V1
Draft version December 9, 2020 Preprint typeset using LATEX style emulateapj v. 12/16/11 ULTRAMASSIVE BLACK HOLES IN THE MOST MASSIVE GALAXIES: MBH − σ VERSUS MBH − RB Bililign T. Dullo,1 Armando Gil de Paz,1 and Johan H. Knapen2,3 1 Departamento de F´ısica de la Tierra y Astrof´ısica, Instituto de F´ısica de Part´ıculas y del Cosmos IPARCOS, Universidad Complutense de Madrid, E-28040 Madrid, Spain; [email protected] 2Instituto de Astrof´ısica de Canarias, V´ıa L´actea S/N, E-38205 La Laguna, Spain and 3Departamento de Astrof´ısica, Universidad de La Laguna, E-38206 La Laguna, Spain Draft version December 9, 2020 ABSTRACT We investigate the nature of the relations between black hole (BH) mass (MBH) and the central velocity dispersion (σ) and, for core-S´ersic galaxies, the size of the depleted core (Rb). Our sample of 144 galaxies with dynamically determined MBH encompasses 24 core-S´ersic galaxies, thought to be products of gas-poor mergers, and reliably identified based on high-resolution HST imaging. For core-S´ersic galaxies—i.e., combining normal-core (Rb < 0.5 kpc) and large-core galaxies (Rb & 0.5 ∝ 1.20±0.14 kpc), we find that MBH correlates remarkably well with Rb such that MBH Rb (rms scatter in log MBH of ∆rms ∼ 0.29 dex), confirming previous works on the same galaxies except three new ones. Separating the sample into S´ersic, normal-core and large-core galaxies, we find that S´ersic 4.88±0.29 and normal-core galaxies jointly define a single log-linear MBH − σ relation MBH ∝ σ with ∆rms ∼ 0.47 dex, however, at the high-mass end large-core galaxies (four with measured MBH) are offset upward from this relation by (2.5 − 4) × σs, explaining the previously reported steepening of the MBH − σ relation for massive galaxies. -

The Peculiar Motions of Early-Type Galaxies in Two Distant Regions. I
Dartmouth College Dartmouth Digital Commons Dartmouth Scholarship Faculty Work 9-1996 The Peculiar Motions of Early-Type Galaxies in Two Distant Regions. I. Cluster and Galaxy Selection Gary Wegner Dartmouth College Matthew Colless Australian National University Glenn Baggley University of Durham Roger L. Davies University of Durham Follow this and additional works at: https://digitalcommons.dartmouth.edu/facoa Part of the External Galaxies Commons Dartmouth Digital Commons Citation Wegner, Gary; Colless, Matthew; Baggley, Glenn; and Davies, Roger L., "The Peculiar Motions of Early-Type Galaxies in Two Distant Regions. I. Cluster and Galaxy Selection" (1996). Dartmouth Scholarship. 2309. https://digitalcommons.dartmouth.edu/facoa/2309 This Article is brought to you for free and open access by the Faculty Work at Dartmouth Digital Commons. It has been accepted for inclusion in Dartmouth Scholarship by an authorized administrator of Dartmouth Digital Commons. For more information, please contact [email protected]. The Astrophysical Journal Supplement Series, 106:1-26,1996 September IW © 1996. The American Astronomical Society. All rights reserved. Printed in U.SA .... THE PECULIAR MOTIONS OF EARLY-TYPE GALAXIES IN TWO DISTANT REGIONS. I. CLUSTER AND GALAXY SELECTION 96ApJS..106 Gary Wegner 19 Department of Physics and Astronomy, 6127 Wilder Laboratory, Dartmouth College, Hanover, NH 03755-3528 Matthew Colless Mount Stromlo and Siding Spring Observatories, Australian National University, Weston Creek, ACT 2611, Australia Glenn Baggley and Roger L. Davies Department of Physics, University of Durham, South Road, Durham DH1 3LE, England Edmund Bertschenger Department of Physics, MIT 6-207, Massachusetts Institute of Technology, Cambridge, MA 02139 David Burstein Department of Physics and Astronomy, Box 871054, Arizona State University, Tempe, AZ 85287-1504 Robert K. -

Download This Article in PDF Format
A&A 516, A1 (2010) Astronomy DOI: 10.1051/0004-6361/200913888 & c ESO 2010 Astrophysics Parsec-scale properties of brightest cluster galaxies E. Liuzzo1,2, G. Giovannini1,2, M. Giroletti1, and G. B. Taylor3,4 1 INAF Istituto di Radioastronomia, via Gobetti 101, 40129 Bologna, Italy e-mail: [email protected] 2 Dipartimento di Astronomia, Università di Bologna, via Ranzani 1, 40127 Bologna, Italy 3 Department of Physics and Astronomy, University of New Mexico, Albuquerque NM 87131, USA 4 also Adjunct Astronomer at the National Radio Astronomy Observatory, USA Received 16 December 2009 / Accepted 1 February 2010 ABSTRACT We present new VLBI observations at 5 GHz of a complete sample of brightest cluster galaxies (BCGs) in nearby Abell clusters (distance class <3). Combined with data from the literature, we provide parsec-scale information for 34 BCGs. Our analysis of the parsec-scale radio emission of BCGs and the cluster X-ray properties finds a possible dichotomy between BCGs in cool-core clusters and those in non-cool-core clusters. Among resolved sources, those in cool-core clusters tend to have two-sided parsec-scale jets, while those in less relaxed clusters have predominantly one-sided parsec-scale jets. We suggest that this difference is caused by the interplay between the jets and the surrounding medium. The one-sided structure in non-cool-core clusters may be due to Doppler boosting effects in relativistic, intrinsically symmetric jets whereas two-sided morphology in cool core clusters is probably related to the presence of heavy and mildly relativistic jets that have been decelerated on the parsec-scale. -

ING Technical Note No. 134 “ING Bibliography and Analysis 2002-2011” - Page 2
ING LA PALMA TECHNICAL NOTE NO. 134 ING Bibliography and Analysis 2002-2011 Javier Méndez (ING) May 2012 Contents 1. Introduction .................................................................................................................................................................... 3 2. Analysis. .......................................................................................................................................................................... 4 2.1. Paper counts. .......................................................................................................................................................... 4 2.2. Paper authorship. .................................................................................................................................................... 7 2.3. Paper instrument use. ............................................................................................................................................. 7 2.4. Paper count check. .................................................................................................................................................. 8 Appendix 1. “ING Bibliography 2002-2011”. ........................................................................................................................ 10 2002 .................................................................................................................................................................................. 10 2003 .................................................................................................................................................................................