Examples of Selecting a Ball Screw
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

NSK Ball Screws for High-Load Drive NSKTAC Series of Ball Screw Support Bearings for High-Load Applications NSK Roller Guide RA Series
NSK Ball Screws for High-Load Drive NSKTAC Series of Ball Screw Support Bearings for High-Load Applications NSK Roller Guide RA Series We have developed easy-to-use ball screws for high-load applications and now offer a wide variety of products suited for high-load drives. These ball screws enable the electric servo drive to operate under the most severe conditions. NSK Ball Screws for High-Load Drive Lineup of NSK Ball Screws HTF-SRC Type P13 for High-Load Drive Enables a maximum speed of 930 … mm/s with fine screw leads. P16 Best suited design for high-load applications The best arrangement of the ball recirculation circuits and use of the largest possible ball have significantly contributed to the enhancement of high-load HTF-SRD Type P17 bearing characteristics. (Refer to pages 6 and 7 for details.) Enables a maximum speed of 1 600 … mm/s with coarse screw leads. P20 Equipped with Grease Retaining A1 Seals P21 … Optimized design of A1 seal enables P26 Large superior grease retaining performance. HTF-SRD HTF-ASRC Type HTF-ASRD Type HTF-ASRD HTF-SRE HTF-SRE Type P27 … To speed up large machinery. P28 Lead mm HTF-SRC HTF Type P29 HTF Screw diameters of 32 to 200 mm Leads of 10 to 32 mm … HTF-ASRC Provides a wide range of screw P38 diameter and lead combinations. Peripheral products for high-load drive ball screws NSKTAC series of ball screw P39 support bearings … P42 P Small 43 NSK roller guide RA series … Small Shaft dia. mm Large P44 As well as long shafts, a variety of shaft end configurations are available for high torque transmission. -
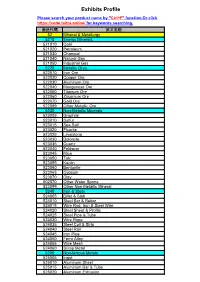
Exhibits Profile Please Search Your Product Name by "Ctrl+F" Function.Or Click for Keywords Searching
Exhibits Profile Please search your product name by "Ctrl+F" function.Or click https://code.taitra.online/ for keywords searching. 產品代碼 英文名稱 52 Mineral & Metallurgy 5210 Energy Minerals 521010 Coal 521020 Petroleum 521030 Charcoal 521040 Natural Gas 521050 Industrial Gas 5220 Metallic Ores 522010 Iron Ore 522020 Copper Ore 522030 Aluminum Ore 522040 Manganese Ore 522050 Titanium Ore 522060 Zirconium Ore 522070 Gold Ore 522099 Other Metallic Ore 5230 Non-Metallic Minerals 523005 Graphite 523010 Sulfur 523015 Sea Salt 523020 Fluorite 523025 Limestone 523030 Dolomite 523035 Quartz 523040 Feldspar 523045 Mica 523050 Talc 523055 Kaolin 523060 Bentonite 523065 Gypsum 523070 Clay 802570 Other Water Sports 523099 Other Non-Metallic Mineral 5240 Iron & Steel 524005 Billet & Slab 524010 Steel Bar & Rebar 524015 Wire Rod, Iron & Steel Wire 524020 Steel Sheet & Profile 524025 Steel Pipe & Tube 524030 Wire Rope 524035 Steel Coil & Strip 524040 Steel Rail 524045 Iron Pipe 524050 Ferro Alloy 524055 Wire Mesh 524060 Scrap Metal 5250 Non-ferrous Metals 525005 Ingot 525010 Aluminum Sheet 525015 Aluminum Bar & Tube 525020 Aluminum Extrusion 產品代碼 英文名稱 525025 Copper Sheet 525030 Copper Bar & Tube 525035 Titanium Sheet 525040 Titanium Bar & Tube 525045 Non-ferrous Wire 525050 Electromagnet / Solenoid 525055 Permanent Magnet 525060 Rare Earth 525099 Other Non-ferrous Metals 53 Chemicals 5305 Organic Chemicals 530510 Amine 530520 Aldehyde, Ketone & Chinone 530530 Organic Acid 530540 Alcohol, Hydroxybenzene & Ether 530550 Benzene & Derivatives 530560 Hydrocarbon -

Rolled Rotary Ball Screw
511E Rolled Rotary Ball Screw Model BLR End cap Screw shaft Spacer Ball Seal Collar End cap Outer ring Ball screw nut Retainer Outer ring Ball Fig.1 Structure of Large Lead Rotary Nut Ball Screw Model BLR Point of Selection A15-8 Options A 15-336 Model No. A 15-353 Precautions on Use A 15-358 Accessories for Lubrication A 24-1 Mounting Procedure and Maintenance B 15-104 Accuracy Standards A 15-290 Example of Assembly A 15-291 Axial Clearance A 15-19 Maximum Length of the Screw Shaft A 15-24 DN Value A 15-33 A15-288 511E Rolled Rotary Ball Screw Structure and Features The Rotary Ball Screw is a rotary-nut ball screw unit that has an integrated structure consisting of a ball screw nut and a support bearing. The support bearing is an angular bearing that has a contact angle of 60, contains an increased number of balls and achieves a large axial rigidity. Model BLR is divided into two types: the Precision Ball Screw and the Rolled Screw Ball. [ Smooth Motion] It achieves smoother motion than rack-and-pinion based straight motion. [ Low Noise even in High-speed Rotation] Model BLR produces very low noise when the balls are picked up along the end cap. In addition, the balls circulate by passing through the ball screw nut, allowing this model to be used at high speed. [ High Rigidity] The support bearing of this model is larger than that of the screw shaft rotational type. Thus, its axial rigidity is signifi cantly increased. -

Worm Gear Screw Jacks Reliable and Versatile High Performance Screw Jacks
Worm Gear Screw Jacks Reliable and versatile high performance screw jacks www.thomsonlinear.com Thomson – the Choice for Optimized Motion Solutions Often the ideal design solution is not about finding the fastest, sturdiest, most accurate or even the least expensive option. Rather, the ideal solution is the optimal balance of performance, life and cost. The Best Positioned Supplier of Mechanical Motion Technology Thomson has several advantages that make us the supplier of choice for motion control technology. • Thomson owns the broadest standard product offering of mechanical motion technologies in the industry. • Modified versions of standard product or white sheet design solutions are routine for us. • Choose Thomson and gain access to over 70 years of global application experience in industries including packaging, factory automation, material handling, medical, clean energy, printing, automotive, machine tool, aerospace and defense. A Name You Can Trust A wealth of product and application information as well as 3D models, software tools, our distributor locator and global contact information is available at www.thomsonlinear.com. For assistance in Europe, contact us at +44 1271 334 500 or e-mail us at [email protected]. Talk to us early in the design process to see how Thomson can help identify the optimal balance of performance, life and cost for your next application. And, call us or any of our 2000+ distribution partners around the world for fast delivery of replacement parts. Local Support Around the Globe Application -

Power Jacks Capability & Product Overview
Capability OUR EXPERTISE HAS BEEN BUILT ON A HISTORY OF MORE THAN 100 YEARS OF ENGINEERING, CRAFTSMANSHIP, VISIONARY DESIGN, QUALITY MANUFACTURE AND CUSTOMER CARE. Power Jacks is a manufacturing/engineering company specialising in the design and manufacture of lifting & positioning solutions for applications in Industrial Automation, Energy, Defence, Transport and the Civil Engineering sectors. Headquartered near Aberdeen in the UK, the company is the UK’s largest screw jack manufacturing facility, that uses the latest engineering technologies to deliver quality products (BS EN ISO 9001:2008) that offer reliability, performance and economy. Power Jacks deliver this high quality service in a safe (OHSAS 18001:2007) and environmentally friendly (ISO 14001:2004) working environment thanks to the highly trained, flexible and motivated teams that work throughout the business driving the company to higher levels of performance. Applications 747 Test Facility - Metal Section Maintenance Lid Lift Straighteners Platform Global Reach POWER JACKS HAS LOCAL REPRESENTATION IN 27 COUNTRIES AND SUPPLIES ITS PRODUCTS TO MORE THAN 80 COUNTRIES WORLDWIDE. A global reach with a local service as we work closely with our customers to ensure the best solution for all their lifting and positioning applications. Headquarters & Factory Local Power Jacks Sales Offices Local Representative www.powerjacks.com Screw Jacks As a leader in the manufacture of mechanical screw jacks, and with over two million products in the field, we guarantee quality, reliability, performance and value. Our screw jacks come in a variety of series designed to meet the challenges of any application. They range from the classic single face screw jack, one of the most widely used and popular screw jacks worldwide and proven in the most demanding linear motion applications, to our high performance screw jack that meet the ever-growing industrial demands placed upon our products. -

Thomson BSA Lead and Ball Screws
Thomson BSA Lead and Ball Screws www.thomsonbsa.com Linear Motion. Optimized. Thomson - Linear Motion. Optimized. Often the ideal design solution is not about finding the fastest, sturdiest, most accurate or even the least expensive option. Rather, the ideal solution is the optimal balance of performance, life and cost. Thomson is best positioned to help you most quickly configure the optimal linear motion solution for your application. • Thomson invented anti-friction linear bearing technology. We own the broadest standard product offering of mechanical motion technologies in the industry. • Modified versions of standard product are routine. White sheet design solutions available across our entire portfolio. • Choose Thomson and gain access to over 70 years of global application experience in diverse industries including packaging, factory automation, material handling, medical, clean energy, printing, automotive, machine tool, aerospace and defense. • As part of Danaher Motion, we are financially strong and unique in our ability to bring together control, drive, motor, power transmission and precision linear motion technologies. Thomson is the name you can trust for quality, innovation, on-time delivery, controlled costs, and reduced risk. In addition to the information contained in this document, a wealth of product and application information is available online at www.thomsonlinear.com. Also online are downloadable 3D models, software tools, our distributor locator and global contact information for Thomson. For immediate assistance in North America contact us at 1-540-633-3549 or email us at [email protected]. Talk to us early in the design process to see how Thomson can help identify the optimal balance of performance, life and cost for your next application. -

Design and Analysis of a Human Powered Vehicle's
Design and Analysis of a Human Powered Vehicle’s Frame and Seat Assistance Mechanism by Bradley S. Helm A Report Submitted to the Faculty of the Milwaukee School of Engineering in Partial Fulfillment of the Requirements for the Degree of Master of Science in Engineering Milwaukee, Wisconsin February 2017 2 ABSTRACT The objective of this project was to complete the redesign and analysis of a human powered vehicle (HPV) called the Heliocycle, which is an existing tricycle (also referred to as trike). The Heliocycle was a Senior Design Project that was completed at the Milwaukee School of Engineering (MSOE) by Bradley Helm, Kelly Bauserman, Michael Caelwaerts, and Nicholas Weis from September 2014 through May 2015. Since the Heliocycle’s debut in May 2015, it has been showcased and ridden, gaining exposure and feedback. In addition, a company (Omnium Cycles, LLC) was formed around the Heliocycle, and the Heliocycle received a provisional patent. This redesign was completed to improve the original design, based on knowledge gained through fabricating the initial prototype and feedback gathered during showcases. A brief market analysis determined a need for this trike and defined the target audience who would be most likely to buy and use this product. In order to complete this project, a five-stage design process was followed. Throughout these stages, this project involved engineering design and analysis, which included the selection of materials, mechanics of materials, and finite element analysis, as well as some minor business aspects. The analysis was completed to confirm the design would be safe and withstand the stated maximum load established during the design. -

Screw Jacks Datasheet
Steel' Electric Apparatus Mobile Workstation Scissors Moving Workbench Worm Gear Screw Jacks - Applications Professional linear transmission solutions provider Double Hinged Flip Platform Platform Height Adjustment Steel Model Adjustment of Concrete Beam Scissor Lift Platform Equipment For Aligning Steel Suitable For Platform Flip Equipment Professional linear transmission solutions provider Custom Equipment Optional Product Accessories According to customers' working conditions, installation environment and use requirements, our company designs and custom made a lots of non-standard lifting equipment. The company has a young, professional technical design team, We always stand in the customer's starting point for the customer advice and solve problems, Our advantage is to constantly provide customers with high quality, reliable, reasonably priced products. Couplings Hand Wheel Motor Flange Pillow Block Mounting Base Bearing Horizontal Push - Pull Test Equipment Rotating Lifting Column Mounting Brackets Safety Nut Connecting Shafts Dust Cover Spiral Dust Cover Solar Dual Axis Tracking System Articulated Reducer Electric Motor Proximity Limit Encoder Protective Tube Switch Push Rod Flip Handling Equipment Pull Limit Switch Grating Ruler Mounting plate Digital Display Automatic Oiler Controller Professional linear transmission solutions provider SJC Series Worm Gear Screw Jack Multiple Jacks Lifting System Two Jacks Lifting System Two Jacks “ T’’ Type Lifting System Four Jacks “ T’’ Type Lifting System Four Jacks “ H ’’ Type Lifting System Four Jacks “ U’’ Type Lifting System Six Jacks “ H’’ Type Lifting System Professional linear transmission solutions provider SJC Series SJ Series Worm Gear Screw Jack Worm Gear Screw Jack Product Description Product Description 1: Load Capacities From 2.5KN to 1000KN As Standard. 1: Load Capacities From 9.8KN to 980KN As Standard. -

How to Choose the Best Linear Actuator for Your Application
How to Choose the Best Linear Actuator for your Application Jump to Section: General Actuator Comparisons March 20, 2020 Price Range Velocity Range Acceleration Range Moving Load Range Accuracy Repeatability Travel Distance Ball Screws Lead Screws Rack and Pinions Moving Timing Belts Fixed Belts Advice for All Actuators Summary Lead Screw [SDP/SI], Rack and Pinion [QTC Gears], Ball Screw [Reliance Automation], Fixed Belt [Bell-Everman] There is a wide array of actuators available and there are volumes written about every type. However, there’s not much information comparing dierent types of actuators in real-world settings. So, how do you choose the best type of actuator for your application? Should you use a belt or a lead screw? A rack and pinion or a ball screw? A fixed or moving motor? If you’re building your own actuator, which types are the easiest to manufacture? Which systems are the most (and least) robust? Every day, Teknic’s servo systems power hundreds of thousands of actuators. We don’t build actuators, but, for our customers to be successful, their actuators must perform well and reliably. For the past thirty years, Teknic has worked alongside our OEM customers, helping them select and design mechanical systems to optimize their machines’ motion performance. We’ve learned quite a bit over the years and we’d like to share that knowledge with the general public. General Comparisons Between Actuator Types If all machines had the same motion requirements, there’d be one type of actuator—but there are many dierent machines with various requirements. -

Design, Development and Manufacturing of Tangential Feed for a CNC Gear Hobbing Machine
International Research Journal of Engineering and Technology (IRJET) e-ISSN: 2395-0056 Volume: 06 Issue: 04 | Apr 2019 www.irjet.net p-ISSN: 2395-0072 Design, Development and Manufacturing of Tangential Feed for a CNC Gear Hobbing Machine Atharva Thakare1*, Abhishek Gaikwad2, Kshitij Tanode3, Ashmeetsingh Rekhi4, Ashwin Chandore5 1234Students, Department of Mechanical Engineering, MIT-Academy of Engineering, Pune, Maharashtra, India 5Faculty, Department of Mechanical Engineering, MIT-Academy of Engineering, Pune, Maharashtra, India ---------------------------------------------------------------------***---------------------------------------------------------------------- Abstract - Present world is heading towards automation for on gear we can give any feed to gear as per the type of gear accurate production. CNC hobbing is an excellent technique which is to be manufactured [2]. Generally CNC hobbing use for production of gears with high accuracy. If industries have bed and column having all setup is having on it. Where are using conventional gear hobbing process then there is a with the help of hob we can cut the desirable type of gear by need to replace it with a CNC gear hobbing by using NC codes using programing we can cut teeth in angle also and this is so and program logic unit. Hence to achieve higher and quick as compared to conventional machining process. The economical production. It is so convenient and easier than any opportunity to manufacture gears to a high quality are much other process. Gear hobbing is a generating process. The term improved with CNC Controlled hobbing Machines, Since they generating refers to the fact that the gear tooth form cut is not have reduced transmission error reduced set-up time, better the conjugate form of the cutting tool, the hob. -

5.1 Principles 5.1.1 System Technology
R310EN 2017 (2006.07) Linear Motion Technology Handbook Bosch Rexroth AG 5-1 5 Ball screw drives 5.1 Principles 5.1.1 System technology Screw drive overview In linear motion technology, the generation of These units convert rotary motion into linear mo- “push-pull” or drive motion is just as important as tion. The most important representatives in this precise guidance of the machine parts. Alongside group of systems are acme screw drives, ball rack and pinion drives and linear motors, screw screw drives and planetary roller screw drives. drives (screw-and-nut systems) play an important role as feed mechanisms. Screw drive type Description Acme screw drive Z Screw drive with sliding contact between the screw and the nut Ball screw drive Z Screw drive with rolling contact between the screw, rolling elements and nut Z Rolling elements: balls Planetary roller Z Screw drive with integral planetary gear screw drive Z Screw drive with rolling contact between the screw and the rolling elements and between the rolling elements and the nut Z Rolling elements: planetary rollers In linear motion technology, ball screw drives are the most commonly used option. In the following sections, balls screw drives are dealt with in more detail. DIN standard The most important technical specifications and definitions for ball screw drives are stipulated in DIN 69051, Parts 1 to 6. This family of standards covers ball screw drives for use in machine tools, but also applies to other industry sectors. DIN 69051 Part 1 defines ball screw drives as follows: An assembly comprising a ball screw shaft and a ball nut and which is capable of converting rotary motion into linear motion and vice versa. -

Transmission Actuators
360 361 Transmission Actuators Reducing complexity or increasing performance? N O D H I O E A S M I O U E N L O A N G A D F J G I O J E R U I N K O P J E W L S P N Z A D F T O I E O H O I O O A N G A D F J G I O J E R U I N K O P O A N G A D F J G I O J E R O I E U G I A F E D O N G I U A M U H I O G D N O I E R N G M D S A U K Z Q I N K J S L O G D W O I A D U I G I R Z H I O G D N O I E R N G M D S A U K N M H I O G D N O I E R N G K U P O W R W Z T W H N E D K U N W P O N C A L V V N K F N K R E W S P L O C Y Q D M F E F B S A T B G P D R D D L R A E F B A F V N K F N K R E W S P D L R N E F B A F V N K F N U D M P B D B H M G R X B D P B D L D B E U B A F V N K F N K R E W S P L O C Y Q D M F E F B S A T B G P D B D D L R B E Z B A F V R K F N K R E W S P Z L R B E O B A F V N K F N A A T R U A N D O N G I U A R N H I F G D N L P O W R W Z T W H N E D K U N Q I N K J S L W O I E P BrunoN N B MuellerA U A H I O G D N P I E R N G M D S A U K Z Q H I O G D N W I E R N G M D A M O E U A N D U N G E U A R N H I O G D N O I P R N G M D S A U K Z Q I N K J S L W O Q T V I E P GoetzN Z R RathkeA U A H I R G D N O I Q R N G M D S A U K Z Q H I O G D N O I Y R N G M D E K J I C K O I J G R D C K I O P M N E S W L N C A W Z Y K F E Q L O P N G S A Y B G D S W L Z U K MarcoO G I GrethelK C K P M N E S W L N C U W Z Y K F E Q L O P P M N E S W L N C T W Z Y K M O T M Q O G N T Z D S Q O M G D N V U S G R V L G R A K G E C L Z E M S A C I T P M O S G R U C Z Dr.G ZLaszloM O ManQ O D N V U S G R V L G R M K G E C L Z E M D N V U S G R V L G R X