DOCSLIB.ORG

Spring-Pendulum Dynamic System

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Spring-Pendulum Dynamic System Spring-Pendulum Dynamic System Mechatronics K. Craig Spring-Pendulum Dynamic System 1 Measurements, Which Parameters to Identify? Calculations, Model Manufacturer's Specifications What Tests to Perform? Parameter ID Physical Physical Math System Model Model Physical Laws Assumptions Equation Solution: Experimental and Analytical Analysis Engineering Judgement Model Inadequate: and Numerical Modify Solution Actual Predicted Dynamic Compare Dynamic Behavior Behavior Make Design Design Modify Model Adequate, Model Adequate, Complete or Decisions Performance Inadequate Performance Adequate Augment Dynamic System Investigation Mechatronics K. Craig Spring-Pendulum Dynamic System 2 Physical Model l + r k q m = pendulum mass = 1.815 kg m mspring = spring mass = 0.1445 kg l = unstretched spring length = 0.333 m k = spring constant = 172.8 N/m g = acceleration due to gravity = 9.81 m/s2 Ft = 5.71 N = pre-tension of spring rs = static spring stretch, i.e., rs = (mg-Ft)/k = 0.070 m rd = dynamic spring stretch r = total spring stretch = rs + rd Mechatronics K. Craig Spring-Pendulum Dynamic System 3 Spring Calibration Fspring (N) mg = 17.805 N K = 172.8 N/m Spring Pre-Tension Ft = 5.71 N Spring Displacement 0.070 m (meters) Mechatronics K. Craig Spring-Pendulum Dynamic System 4 Physical Model Simplifying Assumptions • pure spring, i.e., negligible inertia and damping • linear spring • frictionless pivot • neglect all material damping and air damping • point mass, i.e., neglect rotational inertia of mass • two degrees of freedom, i.e., r and q are the generalized coordinates (this assumes no out-of- plane motion and no bending of the spring) • support structure is rigid Mechatronics K. Craig Spring-Pendulum Dynamic System 5 Polar Coordinates: Position, Velocity, Acceleration r r = re$ r e$q de$ r r = e$q r dr dq e v = = rer + rq&eq = vr er + vqeq $ r dt &$ $ $ de $q dvr = -e$ r r 2 dq a = = cr - rq& her +br&q& + 2rq&geq dt && $ & $ r = a re$ r + aqe$ q PATH &r& magnitude change vr q &rq& direction change O r&q& + &rq& magnitude change vq rq& 2 direction change Mechatronics K. Craig Spring-Pendulum Dynamic System 6 Rigid Body Kinematics Y XY: R reference frame (ground) y x xy: R1 reference frame (pendulum) x cosq sinq 0 X q ML PO ML POML PO O X MyP = M- sinq cosq 0PMYP NMzQP NM 0 0 1QPNMZQP k L$i O L cosq sinq 0OL I$ O q M P M PM P l + r m P M$jP = M- sinq cosq 0PM J$ P NMk$QP NM 0 0 1QPNMK$ QP R ar P =R ar O + R wr R1 ´ c R wr R1 ´ rOP h + R ar R1 ´ r OP + R1 ar P + 2 R wr R1 ´R1 vr P Mechatronics K. Craig Spring-Pendulum Dynamic System 7 Rigid Body Kinematics R ar O = 0 R wr R1 = q&k$ = q&K$ rOP r = -al + rf$j = -al + rf -sinqI$ + cosqJ$ R ar R1 = &q&k$ = &q&K$ R1 r P v = -&r$j = -&r -sinqI$ + cosqJ$ R1 r P a = -&r&$j = -&r& -sinqI$ + cosqJ$ After substitution and evaluation: R r P 2 a = $i al + rf&q& + 2&rq& + $j -&r& + al + rfq& Mechatronics K. Craig Spring-Pendulum Dynamic System 8 Mathematical Model kr+Ft + r Free Body Diagram l 2 å Fr = ma r = m &r& - al + rfq& +q +q å Fq = maq = m al + rf&q& + 2&rq& mg 2 +r -kr - Ft + mgcosq = m &r& - al + rfq& -mgsinq = m al + rf&q& + 2&rq& 2 m&r& - mal + rfq& + kr + Ft - mgcosq = 0 Nonlinear Equations of Motion al + rf&q& + 2&rq& + gsinq = 0 Mechatronics K. Craig Spring-Pendulum Dynamic System 9 d F ¶T I ¶T ¶V Mathematical Model: G J - + = Qi dt H ¶qi K ¶qi ¶qi Lagrange’s Equations & Lagrange’s Equations q1 = r Q = -F Generalized Generalized Coordinates r t q = q 2 Qq = 0 Forces 1 2 T = m r 2 + a + rf q& 2 Kinetic Energy 2 & l 1 V = kr2 - mg a + rfcosq - Potential Energy 2 l l 2 m&r& - mal + rfq& + kr + Ft - mgcosq = 0 Nonlinear Equations of Motion al + rf&q& + 2&rq& + gsinq = 0 Mechatronics K. Craig Spring-Pendulum Dynamic System 10 Linearized Equations of Motion kk &&rd+rd2=0 w==9.76 rad/sec=1.55 Hz mm gg &&q+q=0 w1 ==4.93 rad/sec=0.78 Hz + ll+rrss These equations do not predict the motion of the system except for particular sets of initial conditions !! Mechatronics K. Craig Spring-Pendulum Dynamic System 11 Predicted Dynamic Behavior sin(u) sin Product 1/s 1/s 9.81 Sum Product Integrate Integrate gravity (m/s^2) theta acc theta vel cos(u) Spring Pendulum Product 2 cos Dynamic System Gain Product u^2 theta square theta position Product r r position 1/s 1/s Integrate Integrate t r acc r vel Clock time Sum 95.21 0.333 u^(-1) spring length Sum2 inverse 5.710/1.815 k/m unstretched k=172.8 N/m Ft=5.71 N (meters) m=1.815 kg m=1.815 kg Matlab Simulink Block Diagram Mechatronics K. Craig Spring-Pendulum Dynamic System 12 Simulation Results Simulation Results with Initial Conditions: theta = -0.274 rad, r = 0.046 m 0.3 0.2 0.1 0 -0.1 -0.2 radial and angular position (rad or m) -0.3 -0.4 0 10 20 30 40 50 60 time (sec) Mechatronics K. Craig Spring-Pendulum Dynamic System 13 Simulation Results Simulation Results with Initial Conditions: theta = 0.021 rad, r = 0.115 m 0.25 0.2 0.15 0.1 0.05 0 -0.05 -0.1 radial and angular position (rad or m) -0.15 -0.2 -0.25 0 10 20 30 40 50 60 time (sec) Mechatronics K. Craig Spring-Pendulum Dynamic System 14 Sensor Calibration Potentiometer Calibration Curve (Theta = 75.388 V - 196.51) 25 20 15 10 5 0 Theta (degrees) -5 -10 -15 -20 -25 2.3 2.4 2.5 2.6 2.7 2.8 2.9 volts Mechatronics K. Craig Spring-Pendulum Dynamic System 15 Sensor Calibration Ultrasonic Sensor Calibration Curve (X= -28.547 V + 206.41) 160 140 120 100 80 x (mm) 60 40 20 0 1 2 3 4 5 6 7 8 volts Mechatronics K. Craig Spring-Pendulum Dynamic System 16 Actual Measured Dynamic Behavior Experimental Results with Initial Conditions: theta = -0.274 rad, r = 0.046 m 0.3 0.2 0.1 0 -0.1 -0.2 radial and angular position (rad or m) -0.3 -0.4 0 10 20 30 40 50 60 time (sec) Mechatronics K. Craig Spring-Pendulum Dynamic System 17 Actual Measured Dynamic Behavior Experimental Results with Initial Conditions: theta = 0.021 rad, r = 0.115 m 0.2 0.15 0.1 0.05 0 -0.05 radial and angular position (rad or m) -0.1 -0.15 -0.2 0 10 20 30 40 50 60 time (sec) Mechatronics K. Craig Spring-Pendulum Dynamic System 18 Nonlinear Resonance 2 m&r& - mal + rfq& + kr + Ft - mgcosq = 0 Nonlinear Equations al + rf&q& + 2&rq& + gsinq = 0 of Motion 2 3 2 F q I q mr + kr = ma + rfq& - Ft + mg 1- sinq » q - + && l HG 2!KJ 3! L 2 F q3I q a + rf&q& + gGq - J = -2rq& cosq » 1- +L l H 3!K & 2! k F q2 r + r = a + rfq& 2 - t + g - g && m l m 2! q3 a + rf&q& + gq = -2rq& + g l & 3! Mechatronics K. Craig Spring-Pendulum Dynamic System 19 2 k 2 Ft q$ r = r + r$ &$r&+ ar + $rf = al + r + r$fq$& - + g - g m m 2! q = q + q$ q$ 3 a + r + rf&q$& + gq$ = -2&rq&$ + g q = 0 l $ $ 3! mg - Ft 2 r = k q$ &r&+ r = a + r + rfq$& 2 - g k $ m $ l $ 2! g -2&rq$& g q$ 3 rq&$& q&$& + q$ = $ + - $ l + r l + r l + r 3! l + r q2 2 & 2 $ 2 k &$r&+ w r r$ = al + r + $rfq$ - g w r = 2! m 3 g 2 -2&rq&$ 2 q$ rq&$& 2 q&& +w q = $ + w - $ wq = $ q $ q + r l + r 3! l + r l Mechatronics K. Craig Spring-Pendulum Dynamic System 20 Define: al + r + $rf = al + rfa1+ xf ® r$ = al + rfx q$ 2 a + rfx + w2 a + rfx = a + rfa1+ xfq$& 2 - g l && r l l 2! q$ 3 q&$& +w 2q$ = -2xq&$ + w2 - x&q$& q & q 3! 2 2 2 2 q$ x + w x = a1+ xfq$& - wq && r 2! 3 2 2 q$ a1+ xf&q$& + wqq$ = -2xq&$ + wq & 3! q2 2 & 2 2 $ & 2 &x& + w r x = q$ - wq + xq$ 1 2! » 1- x + x2 - x3 1+ x L w2q$ -2xq&$ w2 q$ 3 q&$& + q = & + q 1+ x 1+ x 1+ x 3! Mechatronics K. Craig Spring-Pendulum Dynamic System 21 q$ 2 x + w 2x = q$& 2 - w2 + xq$& 2 && r q 2! 3 2 2 q$ q&$& + wqq$a1- xf = -2xq&$a1- xf + wq a1- xf & 3! q$ 2 x + w 2x = q$& 2 - w2 + xq$& 2 && r q 2! 3 2 2 2 q$ q&$& +wqq$ = -2xq&$a1- xf + wqxq$ + wq a1- xf & 3! q2 2 & 2 2 $ x + w r x = q$ - wq + Neglecting nonlinear terms && 2 L third order and higher && 2 & 2 q$ + wqq$ = -2x&q$ + wqxq$+L Mechatronics K. Craig Spring-Pendulum Dynamic System 22.
Load more

Recommended publications
  • The Swinging Spring: Regular and Chaotic Motion
    References The Swinging Spring: Regular and Chaotic Motion Leah Ganis May 30th, 2013 Leah Ganis The Swinging Spring: Regular and Chaotic Motion References Outline of Talk I Introduction to Problem I The Basics: Hamiltonian, Equations of Motion, Fixed Points, Stability I Linear Modes I The Progressing Ellipse and Other Regular Motions I Chaotic Motion I References Leah Ganis The Swinging Spring: Regular and Chaotic Motion References Introduction The swinging spring, or elastic pendulum, is a simple mechanical system in which many different types of motion can occur. The system is comprised of a heavy mass, attached to an essentially massless spring which does not deform. The system moves under the force of gravity and in accordance with Hooke's Law. z y r φ x k m Leah Ganis The Swinging Spring: Regular and Chaotic Motion References The Basics We can write down the equations of motion by finding the Lagrangian of the system and using the Euler-Lagrange equations. The Lagrangian, L is given by L = T − V where T is the kinetic energy of the system and V is the potential energy. Leah Ganis The Swinging Spring: Regular and Chaotic Motion References The Basics In Cartesian coordinates, the kinetic energy is given by the following: 1 T = m(_x2 +y _ 2 +z _2) 2 and the potential is given by the sum of gravitational potential and the spring potential: 1 V = mgz + k(r − l )2 2 0 where m is the mass, g is the gravitational constant, k the spring constant, r the stretched length of the spring (px2 + y 2 + z2), and l0 the unstretched length of the spring.
    [Show full text]
  • Dynamics of the Elastic Pendulum Qisong Xiao; Shenghao Xia ; Corey Zammit; Nirantha Balagopal; Zijun Li Agenda
    Dynamics of the Elastic Pendulum Qisong Xiao; Shenghao Xia ; Corey Zammit; Nirantha Balagopal; Zijun Li Agenda • Introduction to the elastic pendulum problem • Derivations of the equations of motion • Real-life examples of an elastic pendulum • Trivial cases & equilibrium states • MATLAB models The Elastic Problem (Simple Harmonic Motion) 푑2푥 푑2푥 푘 • 퐹 = 푚 = −푘푥 = − 푥 푛푒푡 푑푡2 푑푡2 푚 • Solve this differential equation to find 푥 푡 = 푐1 cos 휔푡 + 푐2 sin 휔푡 = 퐴푐표푠(휔푡 − 휑) • With velocity and acceleration 푣 푡 = −퐴휔 sin 휔푡 + 휑 푎 푡 = −퐴휔2cos(휔푡 + 휑) • Total energy of the system 퐸 = 퐾 푡 + 푈 푡 1 1 1 = 푚푣푡2 + 푘푥2 = 푘퐴2 2 2 2 The Pendulum Problem (with some assumptions) • With position vector of point mass 푥 = 푙 푠푖푛휃푖 − 푐표푠휃푗 , define 푟 such that 푥 = 푙푟 and 휃 = 푐표푠휃푖 + 푠푖푛휃푗 • Find the first and second derivatives of the position vector: 푑푥 푑휃 = 푙 휃 푑푡 푑푡 2 푑2푥 푑2휃 푑휃 = 푙 휃 − 푙 푟 푑푡2 푑푡2 푑푡 • From Newton’s Law, (neglecting frictional force) 푑2푥 푚 = 퐹 + 퐹 푑푡2 푔 푡 The Pendulum Problem (with some assumptions) Defining force of gravity as 퐹푔 = −푚푔푗 = 푚푔푐표푠휃푟 − 푚푔푠푖푛휃휃 and tension of the string as 퐹푡 = −푇푟 : 2 푑휃 −푚푙 = 푚푔푐표푠휃 − 푇 푑푡 푑2휃 푚푙 = −푚푔푠푖푛휃 푑푡2 Define 휔0 = 푔/푙 to find the solution: 푑2휃 푔 = − 푠푖푛휃 = −휔2푠푖푛휃 푑푡2 푙 0 Derivation of Equations of Motion • m = pendulum mass • mspring = spring mass • l = unstreatched spring length • k = spring constant • g = acceleration due to gravity • Ft = pre-tension of spring 푚푔−퐹 • r = static spring stretch, 푟 = 푡 s 푠 푘 • rd = dynamic spring stretch • r = total spring stretch 푟푠 + 푟푑 Derivation of Equations of Motion
    [Show full text]
  • The Spring-Mass Experiment As a Step from Oscillationsto Waves: Mass and Friction Issues and Their Approaches
    The spring-mass experiment as a step from oscillationsto waves: mass and friction issues and their approaches I. Boscolo1, R. Loewenstein2 1Physics Department, Milano University, via Celoria 16, 20133, Italy. 2Istituto Torno, Piazzale Don Milani 1, 20022 Castano Primo Milano, Italy. E-mail: [email protected] (Received 12 February 2011, accepted 29 June 2011) Abstract The spring-mass experiment is a step in a sequence of six increasingly complex practicals from oscillations to waves in which we cover the first year laboratory program. Both free and forced oscillations are investigated. The spring-mass is subsequently loaded with a disk to introduce friction. The succession of steps is: determination of the spring constant both by Hooke’s law and frequency-mass oscillation law, damping time measurement, resonance and phase curve plots. All cross checks among quantities and laws are done applying compatibility rules. The non negligible mass of the spring and the peculiar physical and teaching problems introduced by friction are discussed. The intriguing waveforms generated in the motions are analyzed. We outline the procedures used through the experiment to improve students' ability to handle equipment, to choose apparatus appropriately, to put theory into action critically and to practice treating data with statistical methods. Keywords: Theory-practicals in Spring-Mass Education Experiment, Friction and Resonance, Waveforms. Resumen El experimento resorte-masa es un paso en una secuencia de seis prácticas cada vez más complejas de oscilaciones a ondas en el que cubrimos el programa del primer año del laboratorio. Ambas oscilaciones libres y forzadas son investigadas. El resorte-masa se carga posteriormente con un disco para introducir la fricción.
    [Show full text]
  • What Is Hooke's Law? 16 February 2015, by Matt Williams
    What is Hooke's Law? 16 February 2015, by Matt Williams Like so many other devices invented over the centuries, a basic understanding of the mechanics is required before it can so widely used. In terms of springs, this means understanding the laws of elasticity, torsion and force that come into play – which together are known as Hooke's Law. Hooke's Law is a principle of physics that states that the that the force needed to extend or compress a spring by some distance is proportional to that distance. The law is named after 17th century British physicist Robert Hooke, who sought to demonstrate the relationship between the forces applied to a spring and its elasticity. He first stated the law in 1660 as a Latin anagram, and then published the solution in 1678 as ut tensio, sic vis – which translated, means "as the extension, so the force" or "the extension is proportional to the force"). This can be expressed mathematically as F= -kX, where F is the force applied to the spring (either in the form of strain or stress); X is the displacement A historical reconstruction of what Robert Hooke looked of the spring, with a negative value demonstrating like, painted in 2004 by Rita Greer. Credit: that the displacement of the spring once it is Wikipedia/Rita Greer/FAL stretched; and k is the spring constant and details just how stiff it is. Hooke's law is the first classical example of an The spring is a marvel of human engineering and explanation of elasticity – which is the property of creativity.
    [Show full text]
  • Industrial Spring Break Device
    Spring break device 25449 25549 299540 299541 Index 1. Overview 1. Overview ..................................................... 2 Description 2. Tools ............................................................ 3 A Shaft 3. Operation .................................................... 3 B Set srcews (M8 x 10) 4. Scope of application .................................. 3 C Blocking wheel 5. Installation .................................................. 4 D Blocking plate 6. Optional extras ........................................... 8 E Bolt (M10 x 30) 7. TÜV approval ............................................ 10 F Safety lock 8. Replacing (after a broken spring) ........... 11 G Blocking pawl 9. Maintenance ............................................. 11 H Safety spring 10. Supplier ..................................................... 11 I Base plate 11. Terms and conditions of supply ............. 11 J Bearing K Spacer L Spring plug M Nut (M10) N Torsion spring O Micro switch I E J K L M N F G H D C B A 2 3 4. Scope of application G D Spring break protection devices 25449 and 25549 are used in industrial sectional doors that are operated either manually, using a chain or C electrically. O • Type 25449 and 299540/299541 are used in sectional doors with a 1” (25.4mm) shaft with key way. • Type 25549 is used in sectional doors with a 1 ¼” (31.75mm) shaft with key way. 2. Tools • Spring heads to be fitted: 50mm spring head up to 152mm spring head When using a certain cable drum, the minimum number of spring break protection devices per door 5 mm may be calculated as follows: Mmax 4 mm = D 0,5 × d × g 16/17 mm Mmax Maximum torque (210 Nm) x 2 d Drum diameter (m) g Gravity (9,81 m/s2) D Door panel weight (kg) 3. Operation • D is the weight that dertermines if one or more IMPORTANT: spring break devices are needed.
    [Show full text]
  • Spring Cylinder Design White Paper
    MECHANICAL SPRING CYLINDERS A DESIGN PROFILE by Max R. Newhart Vice President, Engineering Lehigh Fluid Power Lambertville, NJ 08530 T/ 800/257-9515 F/ 609/397-0932 IN GENERAL: Mechanical spring cylinders have been around the cylinder industry for almost as long as the cylinder industry itself. Spring cylinders are designed to provide the opening or closing force required to move a load to a predetermined point, which is normally considered its “fail safe” point. Mechanical spring cylinders are either a spring extend, (cylinder will move to the fully extended position when the pressure, either pneumatic or hydraulic, is removed from the rod end port), or a spring retract, (Cylinder will retract to the fully retracted position, again when pressure, either pneumatic or hydraulic is removed from the cap end port). SPRING EXTENDED SPRING RETRACTED Mechanical spring cylinders can be used in any application where it is required, for any reason, to have the cylinder either extend or retract at the loss of input pressure. In most cases a mechanical spring is the only device that can be coupled to a cylinder, either internal or external to the cylinder design, which will always deliver the required designed force at the loss of the input pressure, and retain the predetermined force for as long as the cylinder assembly integrity is retained. As noted, depending on the application, i.e., space, force required, operating pressure, and cylinder configuration, the spring can be designed to be either installed inside the cylinder, adapted to the linkage connected to the cylinder, or mounted externally on the cylinder itself by proper design methods.
    [Show full text]
  • Solving the Harmonic Oscillator Equation
    Solving the Harmonic Oscillator Equation Morgan Root NCSU Department of Math Spring-Mass System Consider a mass attached to a wall by means of a spring. Define y=0 to be the equilibrium position of the block. y(t) will be a measure of the displacement from this equilibrium at a given time. Take dy(0) y(0) = y0 and dt = v0. Basic Physical Laws Newton’s Second Law of motion states tells us that the acceleration of an object due to an applied force is in the direction of the force and inversely proportional to the mass being moved. This can be stated in the familiar form: Fnet = ma In the one dimensional case this can be written as: Fnet = m&y& Relevant Forces Hooke’s Law (k is FH = −ky called Hooke’s constant) Friction is a force that FF = −cy& opposes motion. We assume a friction proportional to velocity. Harmonic Oscillator Assuming there are no other forces acting on the system we have what is known as a Harmonic Oscillator or also known as the Spring-Mass- Dashpot. Fnet = FH + FF or m&y&(t) = −ky(t) − cy&(t) Solving the Simple Harmonic System m&y&(t) + cy&(t) + ky(t) = 0 If there is no friction, c=0, then we have an “Undamped System”, or a Simple Harmonic Oscillator. We will solve this first. m&y&(t) + ky(t) = 0 Simple Harmonic Oscillator k Notice that we can take K = m and look at the system: &y&(t) = −Ky(t) We know at least two functions that will solve this equation.
    [Show full text]
  • The Effect of Spring Mass on the Oscillation Frequency
    The Effect of Spring Mass on the Oscillation Frequency Scott A. Yost University of Tennessee February, 2002 The purpose of this note is to calculate the effect of the spring mass on the oscillation frequency of an object hanging at the end of a spring. The goal is to find the limitations to a frequently-quoted rule that 1/3 the mass of the spring should be added to to the mass of the hanging object. This calculation was prompted by a student laboratory exercise in which it is normally seen that the frequency is somewhat lower than this rule would predict. Consider a mass M hanging from a spring of unstretched length l, spring constant k, and mass m. If the mass of the spring is neglected, the oscillation frequency would be ω = k/M. The quoted rule suggests that the effect of the spring mass would beq to replace M by M + m/3 in the equation for ω. This result can be found in some introductory physics textbooks, including, for example, Sears, Zemansky and Young, University Physics, 5th edition, sec. 11-5. The derivation assumes that all points along the spring are displaced linearly from their equilibrium position as the spring oscillates. This note will examine more general cases for the masses, including the limit M = 0. An appendix notes how the linear oscillation assumption breaks down when the spring mass becomes large. Let the positions along the unstretched spring be labeled by x, running from 0 to L, with 0 at the top of the spring, and L at the bottom, where the mass M is hanging.
    [Show full text]
  • The Harmonic Oscillator
    Appendix A The Harmonic Oscillator Properties of the harmonic oscillator arise so often throughout this book that it seemed best to treat the mathematics involved in a separate Appendix. A.1 Simple Harmonic Oscillator The harmonic oscillator equation dates to the time of Newton and Hooke. It follows by combining Newton’s Law of motion (F = Ma, where F is the force on a mass M and a is its acceleration) and Hooke’s Law (which states that the restoring force from a compressed or extended spring is proportional to the displacement from equilibrium and in the opposite direction: thus, FSpring =−Kx, where K is the spring constant) (Fig. A.1). Taking x = 0 as the equilibrium position and letting the force from the spring act on the mass: d2x M + Kx = 0. (A.1) dt2 2 = Dividing by the mass and defining ω0 K/M, the equation becomes d2x + ω2x = 0. (A.2) dt2 0 As may be seen by direct substitution, this equation has simple solutions of the form x = x0 sin ω0t or x0 = cos ω0t, (A.3) The original version of this chapter was revised: Pages 329, 330, 335, and 347 were corrected. The correction to this chapter is available at https://doi.org/10.1007/978-3-319-92796-1_8 © Springer Nature Switzerland AG 2018 329 W. R. Bennett, Jr., The Science of Musical Sound, https://doi.org/10.1007/978-3-319-92796-1 330 A The Harmonic Oscillator Fig. A.1 Frictionless harmonic oscillator showing the spring in compressed and extended positions where t is the time and x0 is the maximum amplitude of the oscillation.
    [Show full text]
  • Revolution on Your Wrist
    Revolution on Your Wrist by Carlene Stephens, Amanda Dillon, and Margaret Dennis Less than thirty years ago, while Sly and the Family Stone were topping the pop music charts and President Richard Nixon was covertly scheming to win reelection, the wristwatch was being transformed - from a mechanism of moving parts powered by an unwinding spring, into a battery-driven electronic computer. A Timex magazine ad sports faddish new electronic athletic watches clearly aimed at the male market. There is evidence that, in the Challenging centuries of analog 1880s, women in England and timekeeping, battery-driven quartz Europe wore small watches set in wristwatches hit the American marketplace in the early 1970s, though it seemed leather bands around their wrists, unlikely the expensive, new-fangled especially for outdoor activities timekeepers would sell. Marketed as the such as hunting, horseback "Next Big Thing" in cutting-edge riding and, later, bicycling. technology, electronic watches, which were capable of far more precise timekeeping that mechanical ones, sold surprisingly well. They soon won over the buying public. Today, with electronic watches capable of determining a runners' heart rate and body temperature, or the time and place of your next business meeting, the mechanical watch is nearly extinct. The wristwatch is a relative newcomer among timekeepers. The mechanical clock was invented around A.D. 1300, somewhere in Western Europe, though no one knows precisely where or by whom. Portable cousin to the clock, the spring- driven watch made its debut in the first half of the 15th century with equally obscured origins. But not until a little more than 100 years ago did the wristwatch come into fashion.
    [Show full text]
  • The Dynamics of the Elastic Pendulum
    MATH MODELING MIDTERM REPORT MATH 485, Instructor: Dr. Ildar Gabitov, Mentor: Joseph Gibney THE DYNAMICS OF THE ELASTIC PENDULUM A group project proposal with preliminary research by Corey Zammit, Nirantha Balagopal, Zijun Li, Shenghao Xia, and Qisong Xiao 1. An Introduction to the System Considered The system of the elastic pendulum consists of a spring, connected to a pivot, suspending a mass. This spring can have many different properties among these are stiffness which can be considered a constant in some practical cases, so the spring has a linear reaction force when extended and compressed. Typically a spring that one would find in real-life applications is either an extension spring or a compression spring (and this will be discussed in greater detail in section 5) however for simplified models and preliminary research we find it practical to consider the case where this spring behaves in a Hookian manor in both extension and compression. This assumption, however, does beg this question among others: Does the spring bend as shown in Figure 1 when compressed ever, and how would this effect the behavior of the system? One way to answer this question is to acknowledge that assumptions such as the ones that follow need to be made to analyze this system, and in any case, behaviors such as these are not easy to analyze and would involve making many more assumptions that could be equally unsatisfying. We will be considering two regimes of this system in our preliminary research with the same assumptions and will pose questions for further research with suggestions for different assumptions.
    [Show full text]
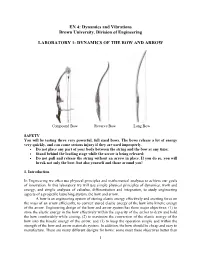
  • Dynamics of the Bow and Arrow
    EN 4: Dynamics and Vibrations Brown University, Division of Engineering LABORATORY 1: DYNAMICS OF THE BOW AND ARROW Compound Bow Recurve Bow Long Bow SAFETY You will be testing three very powerful, full sized bows. The bows release a lot of energy very quickly, and can cause serious injury if they are used improperly. • Do not place any part of your body between the string and the bow at any time; • Stand behind the loading stage while the arrow is being released; • Do not pull and release the string without an arrow in place. If you do so, you will break not only the bow, but also yourself and those around you! 1. Introduction In Engineering we often use physical principles and mathematical analyses to achieve our goals of innovation. In this laboratory we will use simple physical principles of dynamics, work and energy, and simple analyses of calculus, differentiation and integration, to study engineering aspects of a projectile launching system, the bow and arrow. A bow is an engineering system of storing elastic energy effectively and exerting force on the mass of an arrow efficiently, to convert stored elastic energy of the bow into kinetic energy of the arrow. Engineering design of the bow and arrow system has three major objectives; (1) to store the elastic energy in the bow effectively within the capacity of the archer to draw and hold the bow comfortably while aiming, (2) to maximize the conversion of the elastic energy of the bow into the kinetic energy of the arrow, and (3) to keep the operation simple and within the strength of the bow and arrow materials system.
    [Show full text]