DOCSLIB.ORG

GPW and GAPW

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
GPW and GAPW Zurich, July 12th 2017 CP2K : GPW and GAPW Marcella Iannuzzi Department of Chemistry, University of Zurich http://www.cp2k.org Basis Set Representation KS matrix formulation when the wavefunction is expanded into a basis System size {Nel, M}, P [MxM], C [MxN] ⇥i(r)= Cαiφα(r) α Variational n(r)= fiCαiC⇥iφα(r)φ⇥(r)= P⇥φα(r)φ⇥(r) principle i ⇥ ⇥ Constrained minimisation P = PSP problem KS total energy E[ ψ ]=T [ ψ ]+Eext[n]+EH[n]+EXC[n]+EII { i} { i} Matrix formulation of the KS equations H xc K(C)C = T(C)+Vext(C)+E (C)+E (C)=SCε 2 Self-consistency SCF Method Generate a starting density ⇒ ninit Input 3D Coordinates init Generate the KS potential ⇒ VKS of atomic nuclei Solve the KS equations ⇒ , ψ � Initial Guess Molecular Orbitals Fock Matrix (1-electron vectors) Calculation 1 Calculate the new density ⇒ n 1 New KS potential ⇒ VKS Fock Matrix Diagonalization New orbitals and energies ⇒ �1 , ψ Calculate 2 Properties Yes SCF No New density ⇒ n Converged? End ….. until self-consistency 3to required precision Classes of Basis Sets Extended basis sets, PW : condensed matter Localised basis sets centred at atomic positions, GTO Idea of GPW: auxiliary basis set to represent the density Mixed (GTO+PW) to take best of two worlds, GPW Augmented basis set, GAPW: separated hard and soft density domains 4 GPW Ingredients linear scaling KS matrix computation for GTO Gaussian basis sets (many terms analytic) 2 mx my mz ↵mr ⇥i(r)= Cαiφα(r) φ↵(r)= dm↵gm(r) gm(r)=x y z e− α m X Pseudo potentials Plane waves auxiliary basis for Coulomb integrals Regular grids and FFT for the density Sparse matrices (KS and P) Efficient screening G. Lippert et al, Molecular Physics, 92, 477, 1997 J. VandeVondele et al, Comp. Phys. Comm.,167 (2), 103, 2005 5 Gaussian Basis Set Localised, atom-position dependent GTO basis ϕµ(r)= dmµgm(r) m CP2K: Ab initio Molecular Dynamics Simulations Towards Linear Scaling HF/Exact Exchange Summary Acknowledgment Expansion of the density using the density matrix Sparse Matrices n(r)= Pµν ϕµ(r)ϕν∗(r) µν Gaussian basis: • Operator matricesOperator are rather matrices sparse are sparse The sparsity of H and S Sαβ=∫ϕα(r)ϕβ (r)dr Sµ⌫ = 'µ(r)'⌫ (r)dr H αβ=∫ ϕα (r)v(r)ϕβ (r)dr r ϕ (r) Z ϕα ( ) β The sparsity pattern of S and H depends on the basis and the spatial location of the atoms, but not on theH µchemical⌫ = properties'µ(r)V ( ofr) the'⌫ (r)dr system in GGAZ DFT. Sαβ HIV-1 Protease-DMP323 complex in solution (3200 atoms) 6 • Orbital matrices are invariant under unitary transformation The overlap (integral of the product) rapidly decays with the spatial separation of the basis Chemical localization: Boys, Edminston-Rudenberg, etc. functions. Mathematical localization Analytic Integrals Cartesian Gaussian n n n η(r R)2 g(r, n, η, R)=(x R ) x (y R ) y (z R ) z e− − − x − y − z Differential relations @ @ @ n)=2⌘ n + 1i) ni n 1i) n)= n) @Ri | | − | − @Ri | −@ri | Obara-Saika recursion relations (0 (r) 0 ) (a + 1i (r) b) a|O | b |O | Obara and Saika JCP 84 (1986), 3963 7 Basis Set library GTH_BASIS_SETS ; BASIS_MOLOPT ; EMSL_BASIS_SETS O 6-31Gx 6-31G* 4O SZV-MOLOPT-GTHO SZV-GTH SZV-MOLOPT-GTH-q6 1 0 10 6 1 2 0 1 7 1 1 5484.67170000 2 0 1 4 1 1 0.00183110 O 6-311++G3df3pd 6-311++G(3df,3pd) 12.015954705512 -0.060190841200 0.036543638800 825.23495000 8.3043855492 0.01395010 0.1510165999 -0.0995679273 9 5.108150287385 -0.129597923300 0.120927648700 188.04696000 2.4579484191 0.06844510 -0.0393195364 -0.3011422449 1 0 0 6 1 2.048398039874 0.118175889400 0.251093670300 52.96450000 0.23271430 8588.50000000 0.00189515 0.832381575582 0.7597373434 0.462964485000 -0.6971724029 0.352639910300 -0.4750857083 16.89757000 0.47019300 1297.23000000 0.01438590 0.352316246455 0.2136388632 0.450353782600 -0.3841133622 0.294708645200 -0.3798777957 5.79963530 0.35852090 299.29600000 0.07073200 #0.142977330880 0.092715833600 0.173039869300 1 0 1 3 1 1 87.37710000 0.24000100 O0.046760918300 DZVP-GTH -0.000255945800 0.009726110600 15.53961600 -0.11077750 0.07087430 25.67890000 0.59479700 # 23.59993360 -0.14802630 0.33975280 3.74004000 0.28080200 O DZVP-MOLOPT-GTH DZVP-MOLOPT-GTH-q6 21.01376180 0 1 4 2 2 1.13076700 0.72715860 1 0 1 3 1 1 1 1 0 1 1 8.3043855492 1 1 0.1510165999 0.0000000000 -0.0995679273 0.0000000000 42.11750000 0.11388900 0.03651140 2 0 2 7 2 2 1 0.27000580 2.4579484191 1.00000000 -0.0393195364 1.00000000 0.0000000000 -0.3011422449 0.0000000000 9.62837000 0.92081100 0.23715300 12.015954705512 -0.060190841200 0.065738617900 0.036543638800 -0.034210557400 0.014807054400 1 2 2 1 0.7597373434 1 -0.6971724029 0.0000000000 -0.4750857083 0.0000000000 2.85332000 -0.00327447 0.81970200 5.108150287385 -0.129597923300 0.110885902200 0.120927648700 -0.120619770900 0.068186159300 0.80000000 1.00000000 1 0 1 1 1 1 2.048398039874 0.2136388632 0.118175889400 -0.3841133622 -0.053732406400 1.0000000000 0.251093670300 -0.3798777957 -0.213719464600 1.0000000000 0.290576499200 # 0.90566100 1.00000000 1.00000000 0.832381575582 3 2 2 1 1 0.462964485000 -0.572670666200 0.352639910300 -0.473674858400 1.063344189500 O 6-31Gxx 6-31G** 1 0 1 1 1 1 0.352316246455 1.1850000000 0.450353782600 1.0000000000 0.186760006700 0.294708645200 0.484848376400 0.307656114200 4 0.25561100 1.00000000 1.00000000 #0.142977330880 0.092715833600 0.387201458600 0.173039869300 0.717465919700 0.318346834400 1 0 0 6 1 1 2 2 1 1 0.046760918300 -0.000255945800 0.003825849600 0.009726110600 0.032498979400 -0.005771736600 O5484.67170000 TZVP-GTH 0.00183110 5.16000000 1.00000000 # 825.23495000 2 0.01395010 1 2 2 1 1 O TZVP-MOLOPT-GTH TZVP-MOLOPT-GTH-q6 188.04696000 2 0 1 5 3 3 0.06844510 1.29200000 1.00000000 1 52.96450000 10.2674419938 0.23271430 0.0989598460 0.0000000000 0.0000000000 -0.0595856940 1 2 2 1 10.0000000000 0.0000000000 2 0 2 7 3 3 1 16.89757000 3.7480495696 0.47019300 0.1041178339 0.0000000000 0.0000000000 -0.1875649045 0.32250000 0.0000000000 1.00000000 0.0000000000 12.015954705512 -0.060190841200 0.065738617900 0.041006765400 0.036543638800 -0.034210557400 -0.000592640200 0.014807054400 5.79963530 0.35852090 1 3 3 1 1 5.108150287385 1.3308337704 -0.129597923300 -0.3808255700 0.110885902200 0.0000000000 0.080644802300 0.0000000000 0.120927648700 -0.3700707718 -0.120619770900 0.0000000000 0.009852349400 0.0000000000 0.068186159300 1 0 1 3 1 1 1.40000000 1.00000000 2.048398039874 0.4556802254 0.118175889400 -0.6232449802 -0.053732406400 1.0000000000 -0.067639801700 0.0000000000 0.251093670300 -0.4204922615 -0.213719464600 1.0000000000 0.001286509800 0.0000000000 0.290576499200 15.53961600 -0.11077750 0.07087430 1 0 1 1 1 1 0.832381575582 0.1462920596 0.462964485000 -0.1677863491 -0.572670666200 0.0000000000 -0.435078312800 1.0000000000 0.352639910300 -0.2313901687 -0.473674858400 0.0000000000 -0.021872639500 1.0000000000 1.063344189500 3.59993360 -0.14802630 0.33975280 0.08450000 1.00000000 1.00000000 0.352316246455 31.01376180 2 2 1 1 0.450353782600 1.13076700 0.186760006700 0.72715860 0.722792798300 0.294708645200 0.484848376400 0.530504764700 0.307656114200 1 0 0.142977330880 1 1 1.1850000000 1 1 0.092715833600 1.0000000000 0.387201458600 -0.521378340700 0.173039869300 0.717465919700 -0.436184043700 0.318346834400 0.046760918300 0.27000580 -0.000255945800 1.00000000 0.003825849600 1.00000000 0.175643142900 0.009726110600 0.032498979400 0.073329259500 -0.005771736600 1 2 2 1 1 0.80000000 1.00000000 8 GTO in CP2K The repository contains several GTO libraries cp2k/data/ ALL_BASIS_SETS BASIS_RI_cc-TZ GTH_POTENTIALS dftd3.dat ALL_POTENTIALS BASIS_SET HFX_BASIS nm12_parameters.xml BASIS_ADMM BASIS_ZIJLSTRA HF_POTENTIALS rVV10_kernel_table.dat BASIS_ADMM_MOLOPT DFTB MM_POTENTIAL t_c_g.dat BASIS_LRIGPW_AUXMOLOPT ECP_POTENTIALS NLCC_POTENTIALS t_sh_p_s_c.dat BASIS_MOLOPT EMSL_BASIS_SETS POTENTIAL vdW_kernel_table.dat BASIS_MOLOPT_UCL GTH_BASIS_SETS README Tools for the optimisation of GTO basis sets are available in cp2k, based on atomic and molecular electronic structure calculations 9 Pseudopotentials Outline Recap of Previous lecture All electrons vs pseudopotentials The Hartree-Fock-Kohn-Sham method Core electronsClasses of Basis-set are eliminated ZV=Z-Zcore The exchange and correlation hole Condensed phase: Bloch’s th and PBC Solving the electronic problem in practice Atomic 1s : exp{-Z r} Smooth nodeless pseudo-wfn close to nuclei Bare Coulomb replaced by screened Coulomb Inclusion of relativistic effects Transferable Angular dependent potentials: Pt p peaked at 3.9Å s peaked at 2.4Å 10 d peaked at 1.3Å Marialore Sulpizi Density Functional Theory: from theory to Applications GTH Pseudopotentials Norm-conserving, separable, dual-space Local PP : short-range and long-range terms 4 (2i 2) 2 PP PP PP − αPPr Zion PP V (r)= C (2)α r e−( ) erf α r loc i − r i=1 ⇧ ⇤⌃analytically⌅ part of ES ⇥ Non-Local PP with Gaussian type projectors Accurate and PP lm l lm V (r, r0)= r p h p r0 nl h | i i ijh j | i Transferable ij Xlm X Scalar 2 1 r lm l lm (l+2i 2) relativistic r p = N Y (ˆr) r − e− 2 rl | i i “ ” ⇥ Few parameters Goedeker, Teter, Hutter, PRB 54 (1996), 1703; Hartwigsen, Goedeker, Hutter, PRB 58 (1998) 3641 11 Electrostatic Energy Periodic system PP n˜⇤(G)˜n(G) 1 ZAZB EES = Vloc (r)n(r)dr +2⇡⌦ 2 + G 2 RA RB G A=B Z X X6 | − | total charge distribution ntot(r)=n(r)+ nA(r) including n(r) and Z A r R − A ZA rc A ZA r RA n (r)= π 3/2 e A V (r)= erf | − | A c 3 − „ « core − r R rc −(rA) | − A| A ⇥ c PP rA = √2 rlocA cancels the long range term of local PP H E [ntot] long range SR 1 ntot(r)ntot(r) EES = Vloc (r)n(r)+ drdr 2 r r smooth ⌅ ⌅⌅ | − | 1 Z Z R R 1 Z2 + A B erfc | A − B A c c c 2 RA RB 2 2 − ⇥ r A=B (rA) +(rB) ⇥ A 2π A ⇤⇥ | − | ⇤ ⇧ Eov short range, pair Eself 12 Auxiliary Basis Set Long range term : Non-local Hartree potential H 1 ntot(r)ntot(r) E [n ]= drdr tot 2 r r | − | Orthogonal, unbiased, naturally periodic PW basis Efficient Mapping 1 iG r n˜(r)= n˜(G) e · FFT Ω G Grid spacing [Å] 0.15 0.13 0.11 0.10 0.09 0.08 -1 10 H2O, GTH, TZV2P -2 10 -3 Electrostatic Linear scaling solution of the Poisson10 equation -4 10 Energy n˜ (G)˜n -5 (G) H tot∗ Error [a.u.] 10tot E [ntot]=2πΩ -6 G210 G -7 10 100 200 300 400 500 Plane wave cutoff [Ry] 13 Fig.
Load more

Recommended publications
  • An Ab Initio Materials Simulation Code
    CP2K: An ab initio materials simulation code Lianheng Tong Physics on Boat Tutorial , Helsinki, Finland 2015-06-08 Faculty of Natural & Mathematical Sciences Department of Physics Brief Overview • Overview of CP2K - General information about the package - QUICKSTEP: DFT engine • Practical example of using CP2K to generate simulated STM images - Terminal states in AGNR segments with 1H and 2H termination groups What is CP2K? Swiss army knife of molecular simulation www.cp2k.org • Geometry and cell optimisation Energy and • Molecular dynamics (NVE, Force Engine NVT, NPT, Langevin) • STM Images • Sampling energy surfaces (metadynamics) • DFT (LDA, GGA, vdW, • Finding transition states Hybrid) (Nudged Elastic Band) • Quantum Chemistry (MP2, • Path integral molecular RPA) dynamics • Semi-Empirical (DFTB) • Monte Carlo • Classical Force Fields (FIST) • And many more… • Combinations (QM/MM) Development • Freely available, open source, GNU Public License • www.cp2k.org • FORTRAN 95, > 1,000,000 lines of code, very active development (daily commits) • Currently being developed and maintained by community of developers: • Switzerland: Paul Scherrer Institute Switzerland (PSI), Swiss Federal Institute of Technology in Zurich (ETHZ), Universität Zürich (UZH) • USA: IBM Research, Lawrence Livermore National Laboratory (LLNL), Pacific Northwest National Laboratory (PNL) • UK: Edinburgh Parallel Computing Centre (EPCC), King’s College London (KCL), University College London (UCL) • Germany: Ruhr-University Bochum • Others: We welcome contributions from
    [Show full text]
  • Automated Construction of Quantum–Classical Hybrid Models Arxiv:2102.09355V1 [Physics.Chem-Ph] 18 Feb 2021
    Automated construction of quantum{classical hybrid models Christoph Brunken and Markus Reiher∗ ETH Z¨urich, Laboratorium f¨urPhysikalische Chemie, Vladimir-Prelog-Weg 2, 8093 Z¨urich, Switzerland February 18, 2021 Abstract We present a protocol for the fully automated construction of quantum mechanical-(QM){ classical hybrid models by extending our previously reported approach on self-parametri- zing system-focused atomistic models (SFAM) [J. Chem. Theory Comput. 2020, 16 (3), 1646{1665]. In this QM/SFAM approach, the size and composition of the QM region is evaluated in an automated manner based on first principles so that the hybrid model describes the atomic forces in the center of the QM region accurately. This entails the au- tomated construction and evaluation of differently sized QM regions with a bearable com- putational overhead that needs to be paid for automated validation procedures. Applying SFAM for the classical part of the model eliminates any dependence on pre-existing pa- rameters due to its system-focused quantum mechanically derived parametrization. Hence, QM/SFAM is capable of delivering a high fidelity and complete automation. Furthermore, since SFAM parameters are generated for the whole system, our ansatz allows for a con- venient re-definition of the QM region during a molecular exploration. For this purpose, a local re-parametrization scheme is introduced, which efficiently generates additional clas- sical parameters on the fly when new covalent bonds are formed (or broken) and moved to the classical region. arXiv:2102.09355v1 [physics.chem-ph] 18 Feb 2021 ∗Corresponding author; e-mail: [email protected] 1 1 Introduction In contrast to most protocols of computational quantum chemistry that consider isolated molecules, chemical processes can take place in a vast variety of complex environments.
    [Show full text]
  • Starting SCF Calculations by Superposition of Atomic Densities
    Starting SCF Calculations by Superposition of Atomic Densities J. H. VAN LENTHE,1 R. ZWAANS,1 H. J. J. VAN DAM,2 M. F. GUEST2 1Theoretical Chemistry Group (Associated with the Department of Organic Chemistry and Catalysis), Debye Institute, Utrecht University, Padualaan 8, 3584 CH Utrecht, The Netherlands 2CCLRC Daresbury Laboratory, Daresbury WA4 4AD, United Kingdom Received 5 July 2005; Accepted 20 December 2005 DOI 10.1002/jcc.20393 Published online in Wiley InterScience (www.interscience.wiley.com). Abstract: We describe the procedure to start an SCF calculation of the general type from a sum of atomic electron densities, as implemented in GAMESS-UK. Although the procedure is well known for closed-shell calculations and was already suggested when the Direct SCF procedure was proposed, the general procedure is less obvious. For instance, there is no need to converge the corresponding closed-shell Hartree–Fock calculation when dealing with an open-shell species. We describe the various choices and illustrate them with test calculations, showing that the procedure is easier, and on average better, than starting from a converged minimal basis calculation and much better than using a bare nucleus Hamiltonian. © 2006 Wiley Periodicals, Inc. J Comput Chem 27: 926–932, 2006 Key words: SCF calculations; atomic densities Introduction hrstuhl fur Theoretische Chemie, University of Kahrlsruhe, Tur- bomole; http://www.chem-bio.uni-karlsruhe.de/TheoChem/turbo- Any quantum chemical calculation requires properly defined one- mole/),12 GAMESS(US) (Gordon Research Group, GAMESS, electron orbitals. These orbitals are in general determined through http://www.msg.ameslab.gov/GAMESS/GAMESS.html, 2005),13 an iterative Hartree–Fock (HF) or Density Functional (DFT) pro- Spartan (Wavefunction Inc., SPARTAN: http://www.wavefun.
    [Show full text]
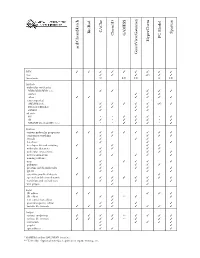
  • D:\Doc\Workshops\2005 Molecular Modeling\Notebook Pages\Software Comparison\Summary.Wpd
    CAChe BioRad Spartan GAMESS Chem3D PC Model HyperChem acd/ChemSketch GaussView/Gaussian WIN TTTT T T T T T mac T T T (T) T T linux/unix U LU LU L LU Methods molecular mechanics MM2/MM3/MM+/etc. T T T T T Amber T T T other TT T T T T semi-empirical AM1/PM3/etc. T T T T T (T) T Extended Hückel T T T T ZINDO T T T ab initio HF * * T T T * T dft T * T T T * T MP2/MP4/G1/G2/CBS-?/etc. * * T T T * T Features various molecular properties T T T T T T T T T conformer searching T T T T T crystals T T T data base T T T developer kit and scripting T T T T molecular dynamics T T T T molecular interactions T T T T movies/animations T T T T T naming software T nmr T T T T T polymers T T T T proteins and biomolecules T T T T T QSAR T T T T scientific graphical objects T T spectral and thermodynamic T T T T T T T T transition and excited state T T T T T web plugin T T Input 2D editor T T T T T 3D editor T T ** T T text conversion editor T protein/sequence editor T T T T various file formats T T T T T T T T Output various renderings T T T T ** T T T T various file formats T T T T ** T T T animation T T T T T graphs T T spreadsheet T T T * GAMESS and/or GAUSSIAN interface ** Text only.
    [Show full text]
  • Kepler Gpus and NVIDIA's Life and Material Science
    LIFE AND MATERIAL SCIENCES Mark Berger; [email protected] Founded 1993 Invented GPU 1999 – Computer Graphics Visual Computing, Supercomputing, Cloud & Mobile Computing NVIDIA - Core Technologies and Brands GPU Mobile Cloud ® ® GeForce Tegra GRID Quadro® , Tesla® Accelerated Computing Multi-core plus Many-cores GPU Accelerator CPU Optimized for Many Optimized for Parallel Tasks Serial Tasks 3-10X+ Comp Thruput 7X Memory Bandwidth 5x Energy Efficiency How GPU Acceleration Works Application Code Compute-Intensive Functions Rest of Sequential 5% of Code CPU Code GPU CPU + GPUs : Two Year Heart Beat 32 Volta Stacked DRAM 16 Maxwell Unified Virtual Memory 8 Kepler Dynamic Parallelism 4 Fermi 2 FP64 DP GFLOPS GFLOPS per DP Watt 1 Tesla 0.5 CUDA 2008 2010 2012 2014 Kepler Features Make GPU Coding Easier Hyper-Q Dynamic Parallelism Speedup Legacy MPI Apps Less Back-Forth, Simpler Code FERMI 1 Work Queue CPU Fermi GPU CPU Kepler GPU KEPLER 32 Concurrent Work Queues Developer Momentum Continues to Grow 100M 430M CUDA –Capable GPUs CUDA-Capable GPUs 150K 1.6M CUDA Downloads CUDA Downloads 1 50 Supercomputer Supercomputers 60 640 University Courses University Courses 4,000 37,000 Academic Papers Academic Papers 2008 2013 Explosive Growth of GPU Accelerated Apps # of Apps Top Scientific Apps 200 61% Increase Molecular AMBER LAMMPS CHARMM NAMD Dynamics GROMACS DL_POLY 150 Quantum QMCPACK Gaussian 40% Increase Quantum Espresso NWChem Chemistry GAMESS-US VASP CAM-SE 100 Climate & COSMO NIM GEOS-5 Weather WRF Chroma GTS 50 Physics Denovo ENZO GTC MILC ANSYS Mechanical ANSYS Fluent 0 CAE MSC Nastran OpenFOAM 2010 2011 2012 SIMULIA Abaqus LS-DYNA Accelerated, In Development NVIDIA GPU Life Science Focus Molecular Dynamics: All codes are available AMBER, CHARMM, DESMOND, DL_POLY, GROMACS, LAMMPS, NAMD Great multi-GPU performance GPU codes: ACEMD, HOOMD-Blue Focus: scaling to large numbers of GPUs Quantum Chemistry: key codes ported or optimizing Active GPU acceleration projects: VASP, NWChem, Gaussian, GAMESS, ABINIT, Quantum Espresso, BigDFT, CP2K, GPAW, etc.
    [Show full text]
  • Modern Quantum Chemistry with [Open]Molcas
    Modern quantum chemistry with [Open]Molcas Cite as: J. Chem. Phys. 152, 214117 (2020); https://doi.org/10.1063/5.0004835 Submitted: 17 February 2020 . Accepted: 11 May 2020 . Published Online: 05 June 2020 Francesco Aquilante , Jochen Autschbach , Alberto Baiardi , Stefano Battaglia , Veniamin A. Borin , Liviu F. Chibotaru , Irene Conti , Luca De Vico , Mickaël Delcey , Ignacio Fdez. Galván , Nicolas Ferré , Leon Freitag , Marco Garavelli , Xuejun Gong , Stefan Knecht , Ernst D. Larsson , Roland Lindh , Marcus Lundberg , Per Åke Malmqvist , Artur Nenov , Jesper Norell , Michael Odelius , Massimo Olivucci , Thomas B. Pedersen , Laura Pedraza-González , Quan M. Phung , Kristine Pierloot , Markus Reiher , Igor Schapiro , Javier Segarra-Martí , Francesco Segatta , Luis Seijo , Saumik Sen , Dumitru-Claudiu Sergentu , Christopher J. Stein , Liviu Ungur , Morgane Vacher , Alessio Valentini , and Valera Veryazov J. Chem. Phys. 152, 214117 (2020); https://doi.org/10.1063/5.0004835 152, 214117 © 2020 Author(s). The Journal ARTICLE of Chemical Physics scitation.org/journal/jcp Modern quantum chemistry with [Open]Molcas Cite as: J. Chem. Phys. 152, 214117 (2020); doi: 10.1063/5.0004835 Submitted: 17 February 2020 • Accepted: 11 May 2020 • Published Online: 5 June 2020 Francesco Aquilante,1,a) Jochen Autschbach,2,b) Alberto Baiardi,3,c) Stefano Battaglia,4,d) Veniamin A. Borin,5,e) Liviu F. Chibotaru,6,f) Irene Conti,7,g) Luca De Vico,8,h) Mickaël Delcey,9,i) Ignacio Fdez. Galván,4,j) Nicolas Ferré,10,k) Leon Freitag,3,l) Marco Garavelli,7,m) Xuejun Gong,11,n) Stefan Knecht,3,o) Ernst D. Larsson,12,p) Roland Lindh,4,q) Marcus Lundberg,9,r) Per Åke Malmqvist,12,s) Artur Nenov,7,t) Jesper Norell,13,u) Michael Odelius,13,v) Massimo Olivucci,8,14,w) Thomas B.
    [Show full text]
  • Benchmarking and Application of Density Functional Methods In
    BENCHMARKING AND APPLICATION OF DENSITY FUNCTIONAL METHODS IN COMPUTATIONAL CHEMISTRY by BRIAN N. PAPAS (Under Direction the of Henry F. Schaefer III) ABSTRACT Density Functional methods were applied to systems of chemical interest. First, the effects of integration grid quadrature choice upon energy precision were documented. This was done through application of DFT theory as implemented in five standard computational chemistry programs to a subset of the G2/97 test set of molecules. Subsequently, the neutral hydrogen-loss radicals of naphthalene, anthracene, tetracene, and pentacene and their anions where characterized using five standard DFT treatments. The global and local electron affinities were computed for the twelve radicals. The results for the 1- naphthalenyl and 2-naphthalenyl radicals were compared to experiment, and it was found that B3LYP appears to be the most reliable functional for this type of system. For the larger systems the predicted site specific adiabatic electron affinities of the radicals are 1.51 eV (1-anthracenyl), 1.46 eV (2-anthracenyl), 1.68 eV (9-anthracenyl); 1.61 eV (1-tetracenyl), 1.56 eV (2-tetracenyl), 1.82 eV (12-tetracenyl); 1.93 eV (14-pentacenyl), 2.01 eV (13-pentacenyl), 1.68 eV (1-pentacenyl), and 1.63 eV (2-pentacenyl). The global minimum for each radical does not have the same hydrogen removed as the global minimum for the analogous anion. With this in mind, the global (or most preferred site) adiabatic electron affinities are 1.37 eV (naphthalenyl), 1.64 eV (anthracenyl), 1.81 eV (tetracenyl), and 1.97 eV (pentacenyl). In later work, ten (scandium through zinc) homonuclear transition metal trimers were studied using one DFT 2 functional.
    [Show full text]
  • Arxiv:1710.00259V1 [Physics.Chem-Ph] 30 Sep 2017 a Relativistically Correct Electron Interaction
    One-step treatment of spin-orbit coupling and electron correlation in large active spaces Bastien Mussard1, ∗ and Sandeep Sharma1, y 1Department of Chemistry and Biochemistry, University of Colorado Boulder, Boulder, CO 80302, USA In this work we demonstrate that the heat bath configuration interaction (HCI) and its semis- tochastic extension can be used to treat relativistic effects and electron correlation on an equal footing in large active spaces to calculate the low energy spectrum of several systems including halogens group atoms (F, Cl, Br, I), coinage atoms (Cu, Au) and the Neptunyl(VI) dioxide radical. This work demonstrates that despite a significant increase in the size of the Hilbert space due to spin symmetry breaking by the spin-orbit coupling terms, HCI retains the ability to discard large parts of the low importance Hilbert space to deliver converged absolute and relative energies. For instance, by using just over 107 determinants we get converged excitation energies for Au atom in an active space containing (150o,25e) which has over 1030 determinants. We also investigate the accuracy of five different two-component relativistic Hamiltonians in which different levels of ap- proximations are made in deriving the one-electron and two-electrons Hamiltonians, ranging from Breit-Pauli (BP) to various flavors of exact two-component (X2C) theory. The relative accuracy of the different Hamiltonians are compared on systems that range in atomic number from first row atoms to actinides. I. INTRODUCTION can become large and it is more appropriate to treat them on an equal footing with the spin-free terms and electron Relativistic effects play an important role in a correlation.
    [Show full text]
  • Jaguar 5.5 User Manual Copyright © 2003 Schrödinger, L.L.C
    Jaguar 5.5 User Manual Copyright © 2003 Schrödinger, L.L.C. All rights reserved. Schrödinger, FirstDiscovery, Glide, Impact, Jaguar, Liaison, LigPrep, Maestro, Prime, QSite, and QikProp are trademarks of Schrödinger, L.L.C. MacroModel is a registered trademark of Schrödinger, L.L.C. To the maximum extent permitted by applicable law, this publication is provided “as is” without warranty of any kind. This publication may contain trademarks of other companies. October 2003 Contents Chapter 1: Introduction.......................................................................................1 1.1 Conventions Used in This Manual.......................................................................2 1.2 Citing Jaguar in Publications ...............................................................................3 Chapter 2: The Maestro Graphical User Interface...........................................5 2.1 Starting Maestro...................................................................................................5 2.2 The Maestro Main Window .................................................................................7 2.3 Maestro Projects ..................................................................................................7 2.4 Building a Structure.............................................................................................9 2.5 Atom Selection ..................................................................................................10 2.6 Toolbar Controls ................................................................................................11
    [Show full text]
  • A Summary of ERCAP Survey of the Users of Top Chemistry Codes
    A survey of codes and algorithms used in NERSC chemical science allocations Lin-Wang Wang NERSC System Architecture Team Lawrence Berkeley National Laboratory We have analyzed the codes and their usages in the NERSC allocations in chemical science category. This is done mainly based on the ERCAP NERSC allocation data. While the MPP hours are based on actually ERCAP award for each account, the time spent on each code within an account is estimated based on the user’s estimated partition (if the user provided such estimation), or based on an equal partition among the codes within an account (if the user did not provide the partition estimation). Everything is based on 2007 allocation, before the computer time of Franklin machine is allocated. Besides the ERCAP data analysis, we have also conducted a direct user survey via email for a few most heavily used codes. We have received responses from 10 users. The user survey not only provide us with the code usage for MPP hours, more importantly, it provides us with information on how the users use their codes, e.g., on which machine, on how many processors, and how long are their simulations? We have the following observations based on our analysis. (1) There are 48 accounts under chemistry category. This is only second to the material science category. The total MPP allocation for these 48 accounts is 7.7 million hours. This is about 12% of the 66.7 MPP hours annually available for the whole NERSC facility (not accounting Franklin). The allocation is very tight. The majority of the accounts are only awarded less than half of what they requested for.
    [Show full text]
  • CHEM:4480 Introduction to Molecular Modeling
    CHEM:4480:001 Introduction to Molecular Modeling Fall 2018 Instructor Dr. Sara E. Mason Office: W339 CB, Phone: (319) 335-2761, Email: [email protected] Lecture 11:00 AM - 12:15 PM, Tuesday/Thursday. Primary Location: W228 CB. Please note that we will often meet in one of the Chemistry Computer Labs. Notice about class being held outside of the primary location will be posted to the course ICON site by 24 hours prior to the start of class. Office Tuesday 12:30-2 PM (EXCEPT for DoC faculty meeting days 9/4, 10/2, 10/9, 11/6, Hour and 12/4), Thursday 12:30-2, or by appointment Department Dr. James Gloer DEO Administrative Office: E331 CB Administrative Phone: (319) 335-1350 Administrative Email: [email protected] Text Instead of a course text, assigned readings will be given throughout the semester in forms such as journal articles or library reserves. Website http://icon.uiowa.edu Course To develop practical skills associated with chemical modeling based on quantum me- Objectives chanics and computational chemistry such as working with shell commands, math- ematical software, and modeling packages. We will also work to develop a basic understanding of quantum mechanics, approximate methods, and electronic struc- ture. Technical computing, pseudopotential generation, density functional theory software, (along with other optional packages) will be used hands-on to gain experi- ence in data manipulation and modeling. We will use both a traditional classroom setting and hands-on learning in computer labs to achieve course goals. Course Topics • Introduction: It’s a quantum world! • Dirac notation and matrix mechanics (a.k.a.
    [Show full text]
  • Trends in Atomistic Simulation Software Usage [1.3]
    A LiveCoMS Perpetual Review Trends in atomistic simulation software usage [1.3] Leopold Talirz1,2,3*, Luca M. Ghiringhelli4, Berend Smit1,3 1Laboratory of Molecular Simulation (LSMO), Institut des Sciences et Ingenierie Chimiques, Valais, École Polytechnique Fédérale de Lausanne, CH-1951 Sion, Switzerland; 2Theory and Simulation of Materials (THEOS), Faculté des Sciences et Techniques de l’Ingénieur, École Polytechnique Fédérale de Lausanne, CH-1015 Lausanne, Switzerland; 3National Centre for Computational Design and Discovery of Novel Materials (MARVEL), École Polytechnique Fédérale de Lausanne, CH-1015 Lausanne, Switzerland; 4The NOMAD Laboratory at the Fritz Haber Institute of the Max Planck Society and Humboldt University, Berlin, Germany This LiveCoMS document is Abstract Driven by the unprecedented computational power available to scientific research, the maintained online on GitHub at https: use of computers in solid-state physics, chemistry and materials science has been on a continuous //github.com/ltalirz/ rise. This review focuses on the software used for the simulation of matter at the atomic scale. We livecoms-atomistic-software; provide a comprehensive overview of major codes in the field, and analyze how citations to these to provide feedback, suggestions, or help codes in the academic literature have evolved since 2010. An interactive version of the underlying improve it, please visit the data set is available at https://atomistic.software. GitHub repository and participate via the issue tracker. This version dated August *For correspondence: 30, 2021 [email protected] (LT) 1 Introduction Gaussian [2], were already released in the 1970s, followed Scientists today have unprecedented access to computa- by force-field codes, such as GROMOS [3], and periodic tional power.
    [Show full text]